基于改进自适应无迹卡尔曼滤波算法的锂电池荷电状态估计
2023-11-15张海涛刘新天
张海涛 刘新天
(合肥工业大学,合肥 230009)
1 前言
电池管理系统(Battery Management System,BMS)控制算法的优劣直接影响电动汽车的安全可靠运行,其中,电池的荷电状态(State Of Charge,SOC)是BMS监测的关键指标[1]。但SOC无法直接获得,需要进行估计。目前,常用的SOC 估算方法主要有安时积分法[2]、开路电压法[3]、数据驱动法[4]和基于模型的方法[5],其中基于模型的估算方法应用较为广泛。由于卡尔曼滤波算法只能解决线性系统问题,国内外研究学者对算法进行改进,提出了扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法和无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法等非线性系统算法。卡尔曼系列滤波算法作为一种递推算法,特点是计算量小、计算速度快,适合在线SOC 估计[6-8]。基于滤波方案的锂离子电池SOC 估计方法一般将电池模型与闭环SOC 估计迭代过程相结合,具有高估计精度和良好的实时性能[9]。在初始参数设置合理的前提下,卡尔曼系列滤波算法的估计误差已被证明呈指数收敛[10]。
但是当前很多滤波算法在实际应用中仍存在一些问题,其中一个重要问题是没有考虑到误差新息序列的振幅分布的变化。通过使用固定长度区间的误差序列来计算新息协方差矩阵,导致无法应对新息协方差矩阵的变化,使得误差增大,甚至估计结果发散。文献[11]采用一种变窗口噪声估计器,通过识别误差新息序列分布的变化,选择分布变化后的误差新息序列更新噪声协方差。但是在其变窗口自适应无迹卡尔曼滤波(Adaptive Unscented Kalman Filter,AUKF)算法设计中,窗口自适应的算法估计结果具有一定波动性,在窗口自适应阶段产生突变,对模型的收敛速度、精确度和稳定性存在一定影响。本文针对这一问题,在误差新息序列的幅值分布发生变化时,改变窗口自适应算法的增减逻辑,使变窗口过程更加平滑,减小因窗口大小突变导致的误差,从而提升算法的精确度和稳定性。采用遗忘递推最小二乘(Forgetting Factor Recursive Least Square,FFRLS)算法对锂电池电路模型参数进行在线辨识,并结合改进的变窗口自适应无迹卡尔曼滤波算法进行锂电池的SOC 估算。最后,通过试验验证,将改进的变窗口AUKF 算法与UKF、AUKF及变窗口AUKF算法进行对比。
2 锂电池建模及参数辨识
2.1 电池模型建立
等效电路模型通过电压源、电阻、电容等元器件组成电路网络结构描述电池的外特性,其能够满足辨识的实时性要求,快速实现电池特性的仿真[12]。考虑电池模型的简易性、计算的简捷性以及能够较好适应BMS 的处理性能,本文以二阶RC 等效电路网络作为研究模型,如图1 所示。其中:UOC为电池开路电压;R0为欧姆内阻;R1、C1分别为极化电阻、极化电容;R2、C2分别为浓差极化电阻、浓差极化电容;U1为电化学极化电压;U2为浓差极化电压;I为充、放电电流;UL为输出端电压。
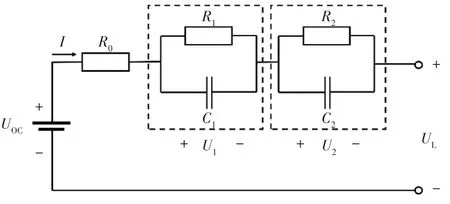
图1 二阶RC等效电路模型
该模型的状态方程与输出方程分别为:
SOC的定义为:
式中,Qt为电池剩余容量;Qn为电池额定容量。
对式(3)进行离散化,可得:
式中,η为电池库仑效率,充电时η<1,放电时η>1;Δt为当前充放电时间;I(k-1)为(k-1)时刻电流。
选择U1、U2、SSOC(k)为状态变量,将式(1)、式(2)离散化,结合式(4),可得观测方程和状态空间方程:
式中,τ1=R1C1、τ2=R2C2为时间常数。
2.2 带遗忘因子的递推最小二乘法
递推最小二乘辨识[13]的主要步骤为:
式中,为k时刻系统估计值系数矩阵;φ(k)为k时刻系统测量矩阵;φT(k)(k-1)、q(k)分别为系统在k时刻的理论观测值和实际观测值;K(k)为k时刻校准值,即系统增益矩阵;P(k)为k时刻协方差矩阵。
在使用递推最小二乘法进行参数辨识的过程中,随着采样次数和数据量的不断增多,矩阵P(k)将逐渐趋于零而出现“数据饱和”现象,从而使得估计算法无法收敛到参数真实值附近。“数据饱和”是指随着递推时间的推移,数据的不断累积导致新数据提供的信息被旧数据所覆盖,新数据的修正作用逐渐减弱,甚至消失的现象。为降低算法对旧数据的信任度,减小其对当前时刻估计结果的影响,突出新数据在辨识过程中的修正作用,引入遗忘因子λ。遗忘因子最小二乘递推辨识[14]的公式为:
式中,E为单位矩阵。
其中,λ的取值范围为0~1,λ越小,算法追踪能力越强,波动也越大,一般取λ=0.95~1。λ=1时算法为递推最小二乘法。
2.3 模型参数在线辨识
根据式(2),进行拉普拉斯(Laplace)变换可得传递函数为:
对式(9)进行双线性离散化处理[15]:
将离散化传递函数转化为时域差分方程:
式中,q(k)=UOC(k)-UL(k);α1、α2、β0、β1、β2为待辨识参数。
状态方程和待辨识参数为:
则式(11)可改写为:
根据文献[16]的方法,系统的传递函数可以改写为:
式中,T为采样时间。
式(9)、式(14)的对应系数相同,可以得到:
进而求得电池待辨识参数,最后传递给SOC 算法进行电池SOC估计。
3 锂电池SOC估计
3.1 自适应无迹卡尔曼滤波算法
与EKF 方法不同,UKF 算法是一种非线性滤波方法,首先确定无迹变换在估计点附近的采样点,再利用这些采样点表示高斯密度函数近似状态的概率密度函数。无迹变换的核心在于按照某一规则选择一些采样点,使选取的采样点的均值和协方差与原状态分布的相同。将这些点代入非线性函数中,得到非线性函数值点集,通过点集获取变换后的均值和协方差。这样得到的非线性变换后的均值和协方差精度最少具有二阶精度。
AUKF 方法的核心在于,在UKF 算法的基础上结合自适应噪声估计器对系统状态变量进行估算。自适应噪声估计器基于协方差匹配原理对测量噪声和过程噪声协方差进行更新。对任意系统,其状态空间方程通常可以写作:
式中,xk为k时刻系统状态矢量;yk为k时刻测量矢量;uk为k时刻输入矢量;wk为k时刻高斯过程噪声;vk为高斯测量噪声;f(xk,uk)为非线性系统函数;g(xk,uk)为非线性测量函数。
AUKF 算法的详细推导过程可参考文献[17],其大致流程如下:
a.状态和误差协方差矩阵初始化;
b.计算西格玛(Sigma)点;
c.时间步更新;
d.测量更新;
e.测量校准;
f.过程和测量噪声协方差更新;
g.更新迭代,重复步骤b~步骤f,以获取最优状态估计。
3.2 变窗口噪声估计器
在AUKF 算法中,采用固定长度的误差新息序列估计新息协方差矩阵。受模型误差、算法近似误差以及放电工况的不确定性等因素影响,误差新息序列的幅值分布不是固定不变的。故应优化算法,更新变化后的误差新息序列估计新息协方差矩阵,进而提高测量和过程噪声协方差矩阵的估计精度。
参考文献[18],设置识别窗口长度为2N,假设识别窗口内的误差新息序列服从高斯白噪声分布,均值为0、方差为σ2。根据高斯分布,识别窗口内的误差新息序列的概率密度函数可以表示为:
式中,ek为k时刻的误差新息值。
变窗口的核心在于:如果误差新息序列分布未发生变化,将增加识别窗口长度;相反,如果误差新息序列分布发生较大变化,在识别窗口内的误差新息序列的概率密度分布可能存在很大不同,继续采用原长度的固定窗口将无法精确估计新息协方差矩阵。因此,需要识别窗口中误差新息序列的概率密度分布变化时刻,并且重新选择误差序列估计新息协方差矩阵。
令wk=ek2,根据随机变量函数的性质,可得wk的累计分布函数:
式中,P为概率;F为分布函数。
对式(18)两边微分,得wk的概率密度函数:
令识别窗口长度内的误差新息序列W=[wk-2N,wk-1],如果窗口内的误差新息序列分布没有发生变化,则W中的误差新息序列的概率密度均服从独立同分布。W的极大似然函数为每个序列的乘积:
对数极大似然函数F1为:
如果窗口内的误差新息序列分布发生变化,每更新一次识别窗口长度,必须对识别窗口中的中间时刻进行检验。如果被检验的时间点刚好是误差新息序列分布变化临界点,则识别窗口中误差新息序列的极大似然函数等于临界点两侧随机变量序列的概率密度函数乘积:
式中,σ21、σ22分别识别窗口临界点前、后序列服从的高斯分布对应的方差。
同上述方法,可得σ21和σ22:
因此,变化后对数极大似然函数F2为:
当F1-F2>TH时,可判断窗口中误差新息序列分布发生变化,其中TH为阈值。通过试验验证,取TH=1.0时的效果最好。F1-F2可以化简为:
窗口长度初始值设置为L0。如果误差新息序列分布没有变化,则增大窗口长度,其最大值为Lmax。同时,为保证数据过渡平滑,原窗口自适应算法在误差序列分布发生变化时,窗口突变过大,窗口序列数据急剧减少,在状态估计时,会导致误差加大,如图2、图3所示。

图2 原自适应算法窗口波动情况
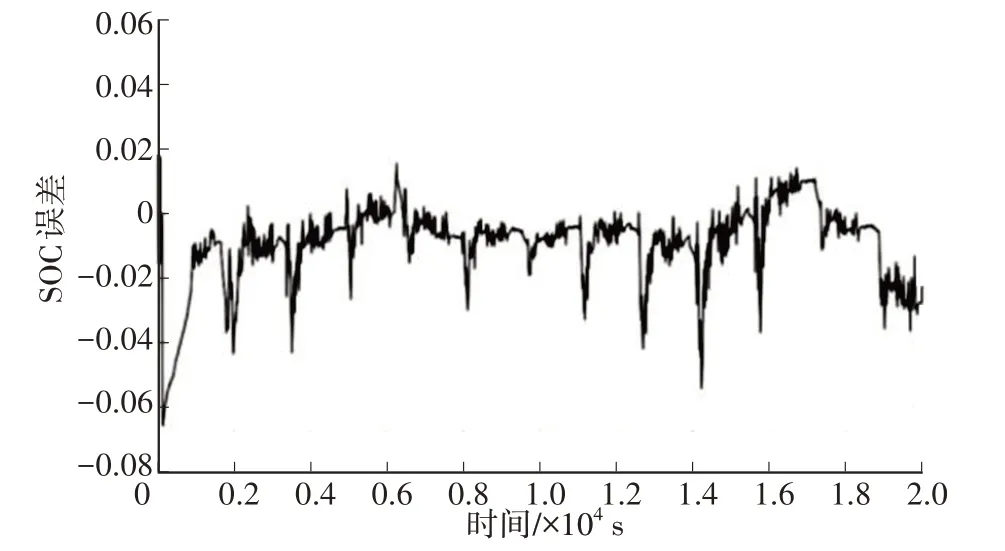
图3 原自适应算法SOC误差
因此,自适应调整公式为:
式中,Lk为k时刻动态窗口长度。
经试验验证,取Lmax=120时效果最好。
调整后的新息协方差矩阵估计方法为:
式中,Hk为k时刻新息噪声协方差;ek为k时刻误差新息。
同时,测量和过程噪声协方差为:
式中,Rk为k时刻测量噪声协方差矩阵;Kk为k时刻卡尔曼增益;Pxx,k|k-1为k时刻误差协方差;Qk为k时刻过程噪声协方差矩阵;Ck=
4 仿真结果与分析
本文选用容量为3 200 mA·h的18650型三元锂电池作为研究对象。在城市道路循环(Urban Dynamometer Driving Schedule,UDDS)工况下验证改进算法的精确度。SOC初始值设定为0.8,实际初始值为1.0。
4.1 确定窗口大小
通过控制变量法进行算法验证,设置阈值TH为1.5,最大窗口大小分别为80、120、160、200。验证SOC 误差结果如图4、表1 所示,采用均方根误差(Root Mean Squared Error,RMSE)和平均绝对误差(Mean Absolute Error,MAE)表征算法误差。

表1 不同最大窗口下SOC均方根误差和平均绝对误差

图4 不同最大窗口SOC误差对比
由表1可以确定,最大窗口大小取120较为合适。
4.2 确定阈值TH
固定最大窗口大小为120,设置阈值TH分别为0.5、1.0、1.5、2.0、2.5,利用控制变量法进行仿真,结果如图5、表2所示。
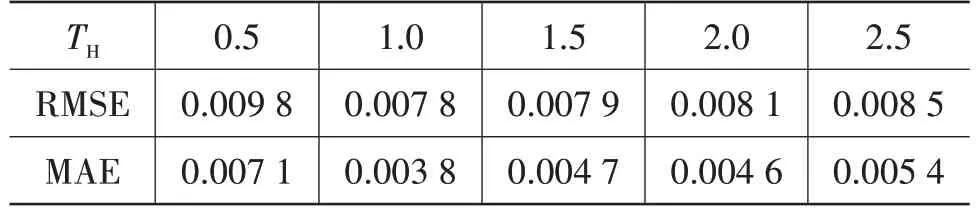
表2 不同阈值下SOC均方根误差和平均绝对误差

图5 不同阈值SOC误差对比
由表2可以确定,取阈值TH=1.0较为合适。
4.3 算法优化前、后对比
通过对自适应窗口算法的改进,取最大窗口大小为120,阈值TH=1.0,窗口变化前、后对比如图6 所示,由图6 可知,窗口大小的波动突变减小,总体较为平滑。算法优化前、后的SOC 误差对比及均方根误差、平均绝对误差如图7 和表3 所示。由仿真结果可知,优化后算法在更新新息协方差时,减小因为新息分布序列大量缺失造成系统估算误差的影响,使得其快速跟踪能力,稳定性以及精确度提升明显。

图6 算法改进前、后窗口变化

图7 算法改进前、后SOC误差对比
将改进后的算法与UKF 和AUKF 算法进行对比,结果如图8 所示。由图8 可知,改进后的AUKF前期由于窗口数量较少,SOC估计误差略有波动,但在后期趋于收敛且稳定性均优于UKF 和AUKF 算法,整体性能指标如表4所示。
5 结束语
本文采用二阶RC 等效电路模型模拟电池动态特性,结合带遗忘因子的最小二乘法进行模型参数在线辨识。结合辨识结果,采用改进后的变窗口自适应无迹卡尔曼滤波方法进行SOC 估计。由仿真对比结果可知,改进后的算法精度和稳定性均明显提升,收敛速度更快。
