基于三维花卉模型的纬编提花织物设计

商林婧, 张爱军, 张燕婷

(江南大学 针织技术教育部工程研究中心,江苏 无锡 214122)

花型意匠图的绘制是针织服装设计中一个必不可少的过程。根据纹样结合织物组织将花型放大并点绘在一定规格的意匠纸上的图样叫作意匠图。传统绘制意匠图的方式都是人工手绘,不仅费时费力,而且对于一些没有美术功底的工作人员来说,完成一幅美观的意匠图需要花费大量的时间。

在针织意匠图的设计过程中,花卉作为一种常用的提花图案,由于其结构复杂且种类繁多,设计人员需要耗费更长的时间来绘制。因此,针对现有花卉类型的针织意匠图生成过程复杂、耗费时间长等问题,本文提出了一种基于三维数据的针织意匠图生成算法。即将二维的花卉图片以3D模型的形式呈现,再转换为二维图像自动生成意匠图,无需手工绘制,在一定程度上可以节省人力、提高工作效率。近年来,国内外许多学者针对基于图像的花卉建模进行了一系列的研究工作,主要是通过以下方式来获取二维图像缺失的深度信息,如引入几何投影、用户的手绘信息等。Ijiri等[1]将花朵的建模过程分为几何编辑与结构编辑两部分,采用从局部到整体的建模方式组合生成结构复杂的花朵模型。Xue等[2]采用平面几何的方法来拟合物体,并利用物体的对称性对生成的点云进行优化处理。Yan等[3]假定花朵为一个三维圆锥,通过该圆锥拟合花朵生成一个花瓣模板模型,并将模型投影到二维图像上,对每个花瓣进行细节调整,重建出十分逼真的花朵模型。缪永伟等[4]通过交互式建模方法,在图像上提取花卉的外围轮廓,并利用镜像对称原理求取二维轮廓的三维信息。林家贤[5]等通过编码器—解码器网络结构生成了花朵不同视角下的RGB图和深度图。何振邦等[6]对用户手绘信息进行预处理和分析,并结合植物学知识来恢复花朵的深度信息。殷悦等[7]采用SURF特征检测算法和SIFT特征匹配算法将植物的二维数据转化为三维坐标,从而得到逼真的三维植物模型。娄路等[8]采用深度卷积神经网络Mask-RCNN对植物茎叶进行分割并提取其特征。综上,基于图像的花朵建模以图像信息为出发点,不仅获取途径多样,而且可以捕捉到物体的真实形态。

本文首先以二维图像为基础,根据正投影原理和镜像对称原理,将花朵拟合为一个三维圆锥,求取二维图像缺失的三维深度数据,建立一个具有真实感的三维模型;其次在用户绘制的二维椭圆基础上,采用变换矩阵,将三维模型根据二维椭圆进行相应的变换,形成多角度的模型;最后生成针织意匠图并织成相应的织物。通过三维模型生成的针织意匠图,不仅提高了工作效率,而且用户可以根据自己的需求,调整模型的角度,生成多个针织图案。

1 基于二维图像的花卉三维模型建立

通过分析二维图像中花朵的结构,将花朵拟合为一个具有一定倾斜度的三维圆锥来粗略估计花的几何形状及方向,假设圆锥体的顶端位于花的中心,花瓣大致位于圆锥体的表面,以此来求得花朵的深度信息。

1.1 用户交互

本文以一个六瓣花朵的花卉为例,在花朵建模之前,用户交互式描绘出二维图像中每个花瓣的两条轮廓曲线CL和CR,若第一条曲线CL的采样点总数为10,则按照{P1,P1L,1,P1L,2,…,P1L,8,E1}的顺序保存这条曲线上的离散采样点,如图1(a)所示。后期需要将每个花瓣的一对对称二维曲线进行三维深度值的恢复,如图1(b)所示。将每个花瓣的两条边缘曲线的共同起点设为P1、P2、P3、P4、P5、P6,存放入一个集合V1,再将两条边缘曲线的终点E1、E2、E3、…、E12存入另一个集合V2中。利用最小二乘法[9]将集合V1中的数据拟合出一个椭圆e1,其圆心为O1,该椭圆即为后期拟合出的三维圆锥底面圆在XOY平面上所得的投影。将V2中的数据采用同样的方法拟合出椭圆e2,则e2的圆心视为二维图像中花朵的花心,也是三维圆锥的顶点O2(图1(c))。

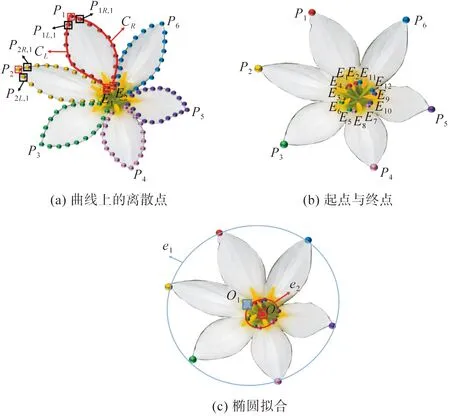
图1 采样点与椭圆拟合

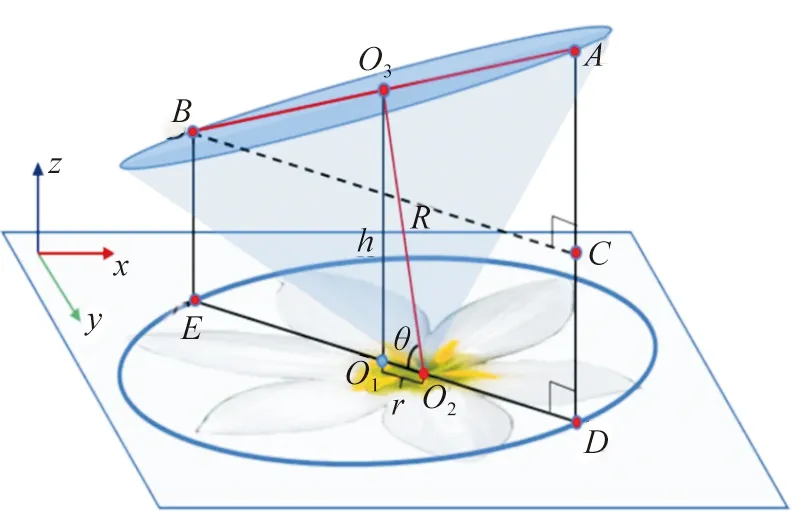
图2 拟合圆锥

1.2 拟合三维圆锥

假定花朵模型为一个具有一定倾斜度的三维圆锥,并将上一步骤中由花瓣起点拟合得到的椭圆e1视为圆锥经过平行投影得到的图形,如图2所示。椭圆e1的圆心为O1,该点也是三维圆锥底面圆的圆心O3在XOY面上的投影点,由该椭圆也可得到其长短轴a和b。由正投影原理可知,线段AB在XOY平面上的投影线为DE,并且图2中三角形ABC与三角形O2O3O1相似,因此可以求得三维圆锥的高R与O2O1之间的长度r的比值,如下式所示:

(1)

式中:AB为圆锥底面直径,长度等于椭圆e1的长轴a,BC长度等于椭圆e1的短轴b。

根据式(1)可以求出R,而三角形O2O3O1为直角三角形,因此也可求出圆锥的倾斜角度θ及圆锥底面圆心O3到XOY平面的垂直高度h。

1.3 求花瓣三维深度

1.3.1 求对称面法向量

绝大多数的花朵在结构中会表现出一定的对称性,主要表现为两侧对称和辐射对称两种方式[10]。将花朵的花瓣视为一个对称的物体,将二维图片中每个花瓣的起点Pi在三维空间中对应的点pi与圆锥底面圆心O3及花心O2组成的平面设为每个立体花瓣的对称面,如图3所示。

图3 对称面和法向量

本文以第六片花瓣为例,其对称面为p6、O3、O2,设N为其对称面的法向量。由于点O2和O1都在XOY平面上,且O1为O3在XOY面上的投影点,可知点O3的z坐标值是点O2的z坐标值与高度h的和。另外,由于点O2、O3、p6的x坐标和y坐标已知,O3、p6的z坐标之差可由下式推导得出:

O3z-p6z=[(O3x-O2x)·(O3x-p6x)+(O3y-O2y)·(O3y-p6y)]/(-h)

(2)

因此该对称面的法向量N可由向量O2O3和p6O3叉乘求得。求出法向量N后,后续即可根据该法向量及二维图形中的一对对称点坐标,并结合镜像对称原理求得对称点的三维深度信息。

1.3.2 求三维深度

求出每个花瓣的对称面及相应的法向量后,即可求得两条对称曲线中每对对称点的三维深度,如图4所示。

图4 根据镜像对称求深度值

根据关于镜面对称的两个特性,1) 两点连线垂直于对称面,且两点到对称面的距离相等;2) 两点的垂直平分线垂直于对称面的法向量[9],可得:

(p6R,3+p6L,3)·N=0

(3)

(p6R,3-p6L,3)·N⊥=0

(4)

式中:p6L,3和p6R,3为三维空间中的一对对称点,N为这两点镜像对称的对称面的法向量,N⊥为垂直于N的某一向量。

设p6L,3=(x1,y1,z1),p6R,3=(x2,y2,z2),N=(nx,ny,nz),N⊥=(-nz,0,nx),代入下式,可计算出p6L,3和p6R,3的z坐标:

(5)

(6)

将每对对称点代入式(5)(6),即可计算得到每两条对称曲线上对称点的三维深度,从而可以得到每个花瓣的边缘曲线深度。

1.3.3 生成花瓣曲面

获得花瓣的三维边缘点之后,还需要生成花瓣曲面。由于花瓣并不是扁平的,花瓣中心具有一定的内凹趋势,本文将花瓣的凹陷程度视为与之横向长度对应的正弦函数。将每个花瓣中的两条三维边缘曲线重新采样,两两相对的采样点组成一对对称点,进行横向的均匀插值,将这些插值点作为初步的花瓣网格模型顶点,如图5所示。

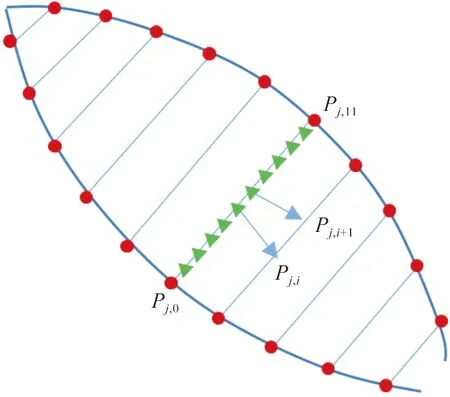
图5 每对对称点之间进行横向均匀插值

本文改进了濮群等[11]在二维平面中计算花朵内凹趋势的研究方法,直接在三维空间中将三角函数在一个周期内的弯曲特性作为花瓣曲面中三维点的内凹趋势,如图6所示。

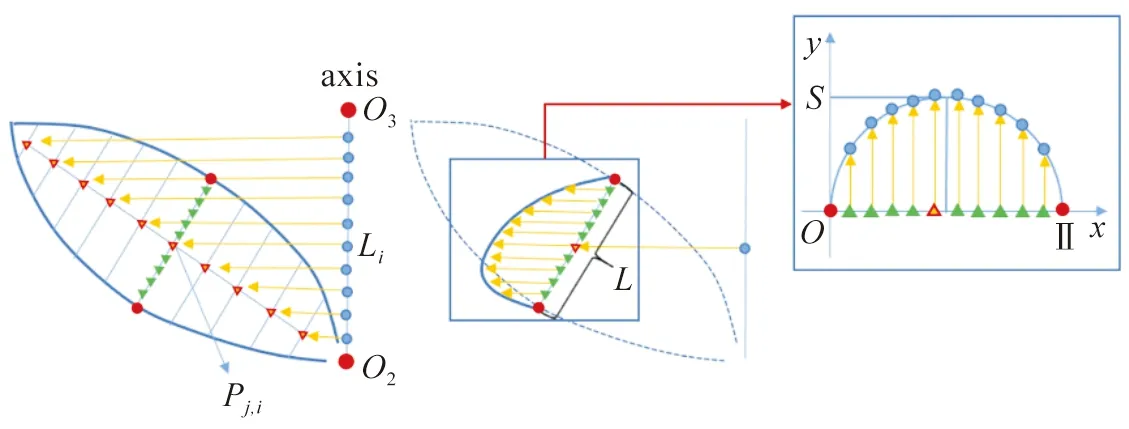
图6 横向采样点移动的方向和距离

首先计算出每对对称点之间的长度L,依据先验知识,葱兰花花瓣的内凹趋势并不明显,因此可以将正弦函数的振幅S设为L的20%～40%。将三角函数的周期t设为横向采样点的总个数,计算如下式所示:

(7)

式中:i为横向绿色三角形插值点的索引号。

对三维圆锥底面圆心O3和花心O2所连线段axis进行采样,该线段上的采样点数目与三维边缘曲线上的采样点数目相等,如图6所示。选取每条横向采样点点集中的中点Pj,i,将其与axis上对应的蓝色采样点Li进行连接,该向量即为横向采样点需要移动的方向。每个横向采样点移动的距离即为式(7)中对应的y值。横向采样点移动到新的位置后,将新的横向采样点按照Pj,i+1、Pj,i、Pj+1,i的顺序依次连接,形成三角面片;然后再按Pj+1,i+1、Pj,i+1、Pj+1,i的顺序将三角面片补齐,形成完整的花瓣曲面,如图7所示。

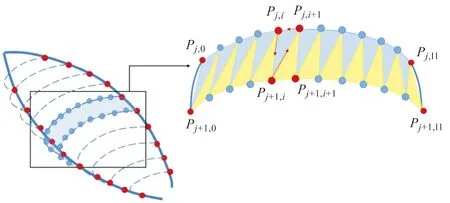
图7 三角面片和花瓣曲面的生成

按照上述顺序在花瓣的每两组对称点之间横向插值,再依次生成三角面片,从而形成完整的花瓣模型。图8为最终形成的三维花朵模型。

图8 花朵模型

2 三维模型的空间变换

考虑到花瓣顶点构成的圆在平面上的投影近似椭圆,本文制作了一个可供用户绘制椭圆的界面。在该界面,用户可通过鼠标操作来控制椭圆的大小及位置,并且可以通过此二维椭圆来改变花朵形态,从而生成多种角度的二维图案。

2.1 椭圆绘制界面的制作

利用MFC制作一个可供用户通过鼠标操作来绘制椭圆的界面,如图9所示。用户首先通过鼠标点击来确定椭圆的中心位置C,确定椭圆位置后会自动生成两个坐标点A和B。移动A点和B点可以调整椭圆长半轴a和短半轴b的具体长度,从而通过改变椭圆的大小及倾斜度来改变花朵模型。

图9 二维椭圆和三维模型

将(0,0)点设为视口的左下角坐标,将屏幕的长cx和宽cy设为视口的右上角坐标。根据A、B点及椭圆圆心C点在绘制椭圆界面上的像素坐标点,按式来计算A、B、C三点在屏幕中显示的新坐标点A′、B′、C′。

(8)

式中:i为A、B、C三点的索引号。

图9为初始模型根据二维椭圆变换后的最终效果,即选取了三种不同大小及倾斜程度的椭圆进行实验,结果表明模型变换效果良好。图9(a)为绘制界面中三种不同形状的椭圆,图9(b)为两种花卉三维模型根据椭圆信息变换后的效果。

2.2 三维模型位置的初步调整

将本文中建立的花朵模型视为一个规则的三维圆锥,因此可以将每个花瓣的顶点所围成的图形视为一个规则的圆形,将该圆形的圆心O3与圆锥顶点O2的连线视为圆锥的中轴,如图10所示。首先将该圆形平面平移,使得圆心O3与原点(0,0,0)重合,将向量O3O2归一化,再将圆锥根据下式经过旋转变换,使其与Z轴平行。

z=(0,0,-1)

(9)

NR=O3O2×z

(10)

cosσ=O3O2·z

(11)

式中:NR为三维模型进行初步旋转的旋转轴,σ为旋转角度。

图10 模型的初步变换

2.3 基于椭圆信息的模型变换

初步变换后的圆锥中轴O3O2与Z轴平行且底面圆心与原点重合,因此可将圆锥的底面圆所在平面视为用户绘制椭圆的界面。底面经过一定旋转,在XOY平面上的正交投影可变为与用户绘制椭圆相近的形状,如图11(沿Z轴方向看,也可称为俯视图)所示。首先根据A′、B′及椭圆圆心C′的坐标计算出椭圆的长半轴a与短半轴b,以及椭圆长半轴a与圆半径k的比值m。利用缩放矩阵,将模型沿着X轴、Y轴、Z轴同时缩放m倍。经过缩放后的花朵模型中,花瓣顶点拟合出的圆形,其半径与绘制椭圆的长半轴大小相等。

(12)

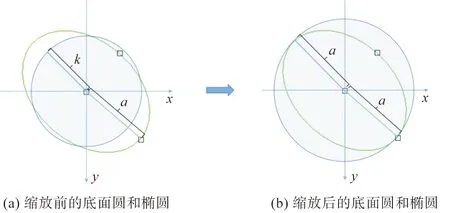
图11 缩放模型

假设空间坐标系水平向右为X轴正方向,垂直屏幕指向用户为Z轴负方向,垂直向上为Y轴正方向。在XOY平面上的具有同样大小和倾斜角度的椭圆,可以由中轴与Z轴平行的三维圆锥经过4种不同的旋转方式近似得到。本文以图11中的椭圆为例,圆锥可按以下4种方式旋转:1) 若三维圆锥的中轴O3O2指向Z轴的正方向,将圆锥沿A′C′所在轴线顺时针旋转一定角度β,可得一中轴指向右上方的三维圆锥。2) 若三维圆锥的中轴O3O2指向Z轴的正方向,将圆锥沿A′C′所在轴线逆时针旋转一定角度β,可得一中轴指向左上方的三维圆锥。3) 若三维圆锥的中轴O3O2指向Z轴的负方向,将圆锥沿A′C′所在轴线顺时针旋转一定角度β,可得一中轴指向左下方的三维圆锥。4) 若三维圆锥的中轴O3O2指向Z轴的负方向,将圆锥沿A′C′所在轴线逆时针旋转一定角度β,可得一中轴指向右下方的三维圆锥。而在前文三维模型的初步变换中,选取的三维向量z(0,0,-1)指向Z轴的负方向,因此选择第三种旋转方式,如图12所示。

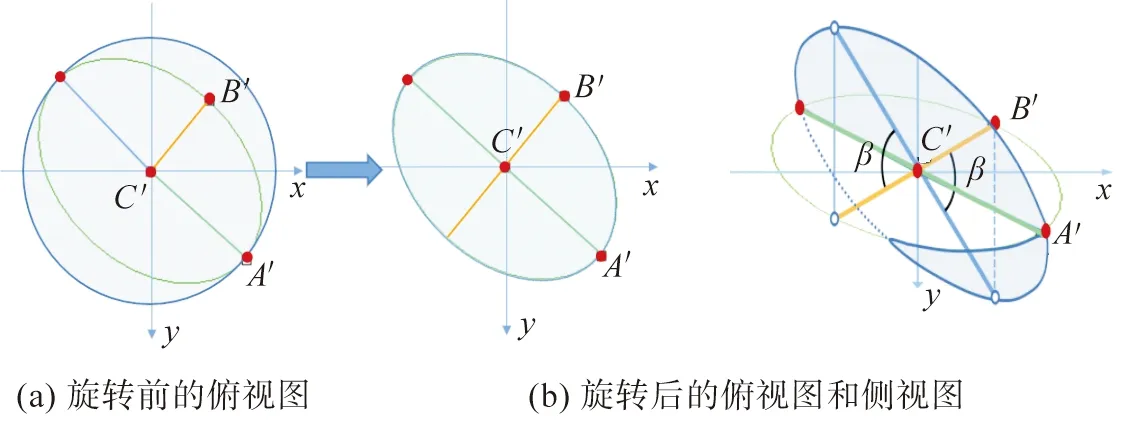
图12 旋转模型

将缩放过后的模型沿着A′C′所在轴线进行顺时针旋转,旋转角度为β,如图12(b)所示。根据式(13～16)可计算出模型的旋转轴L及旋转角β。其中,由于旋转轴L在XOY平面上,因此其z坐标值为0。利用旋转矩阵,将模型的每个三维点进行旋转,旋转后的三维花朵模型,花瓣顶点拟合出的圆在XOY平面上的正交投影形状大致与用户绘制的椭圆相近。

(13)

(14)

(15)

(16)

若在绘制界面中存在多个椭圆,且每个椭圆的大小及倾斜角度不一,需要将每个三维模型在原点经过缩放、旋转变换后,移动到椭圆圆心即C′的坐标位置,形成最终图案。利用平移矩阵,再将模型的每个三维点进行平移,如图13所示。

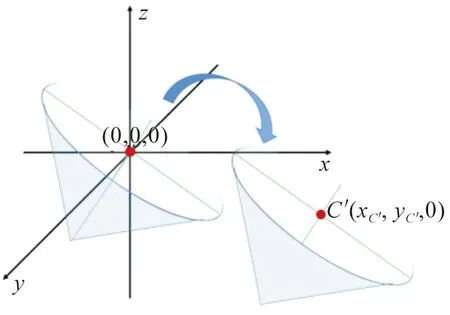
图13 平移模型

模型经过上述三个步骤之后,就可以转变为与二维椭圆大小、方向一致的三维模型。

(17)

3 生成针织意匠图并上机织造

3.1 生成意匠图

将绘制的椭圆图案以三维模型代替后,由于每一朵三维花朵方向大小不同,与光源的相对位置不同,渲染后每朵花的明暗亦不同,渲染后为24位真彩色,而提花织物常用2色、3色提花,一般不超过5色,因此需要使用减色算法[12]将其减为合适的颜色数。

减色后的图案由黑、白、灰三种颜色组成,对应提花图案中三种不同的层次,其中白色作为图案的背景色,灰色作为过渡色,黑色作为花朵上边缘处最深的阴影色。为了让生成的意匠图更具立体感,本文将图案中占有较大面积且随机分布的灰色进行组织填充,填充为一隔一的过渡色,从而形成具有渐变效果的意匠图(图14)。图14(a)为绘制的二维椭圆图案,图14(b)为根据椭圆生成的三维模型,图14(c)为最终生成的意匠图,其中上部的放大图表示一隔一过渡色区域,下部的放大图表示花朵边缘最深的阴影色,即纯黑色区域。

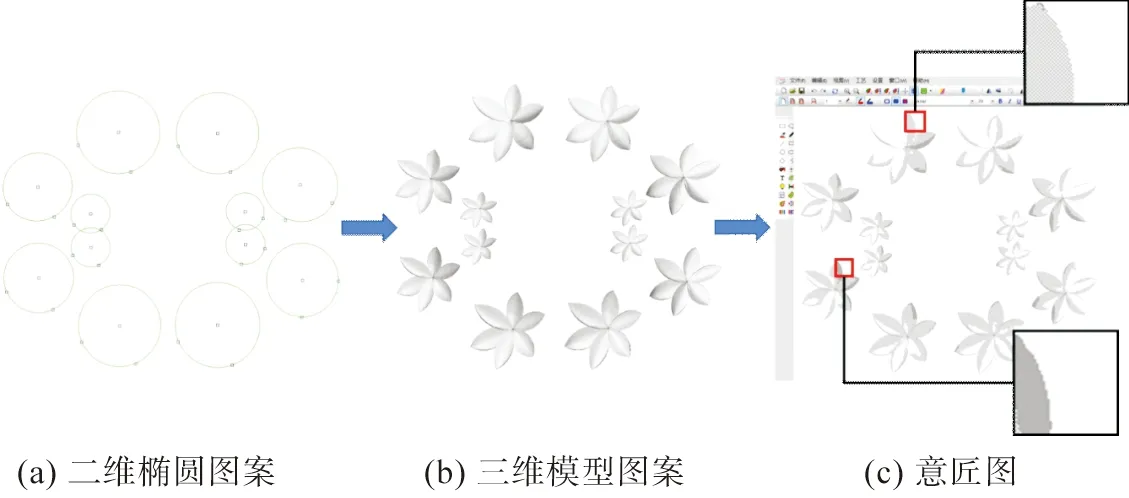
图14 从模型到意匠图的实现步骤

3.2 工艺反面设计和上机实验

经过填色的花型意匠图表示的是织物正面线圈形成的图案,还不能直接用于生产,这是因为提花织物的工艺反面织物可能存在较长的浮线。长浮线会影响编织的连续进行,并且在织物使用过程中浮线容易被勾断从而缩短生命期限。为克服这一缺陷,在设计时可以在长浮线区域间隔地配置成圈或集圈,让浮线长度变短。成圈组织会形成完整线圈,破坏正面提花效果,不是理想的选择。集圈组织不会单独形成完整线圈,其纱线悬挂在其他线圈的后面,因而不易在织物提花面显露,是缩短浮线常用的方式。因此本文实验选择在长浮线区域间隔配置集圈组织。

集圈组织点一般在编织意匠图上配置,编织意匠图的高度为花型意匠图高度和色纱数的乘积。集圈的排列方式和数量会关系到纱线的消耗、织物平方米质量、延伸性等,需要合理配置。一般可以沿纵行方向和斜向配置集圈点,其中斜向配置更加常见。对一般提花织物,将浮线长度控制在3～4针即可有效减少钩丝现象。实验使用的花型意匠图上有大片的白色背景,该区域在织物反面相邻路上的黑色纱线形成长浮线。在每一路上隔3个浮线组织点配置一个集圈点,并将集圈点逐路向右移动一针。体现在织物上,上一横列黑纱集圈点正好在下一横列两个黑纱集圈的中间,两边对称,集圈点分布均匀,织物平整,如图15(e)右侧的局部放大图所示。添加完集圈组织点的意匠图即可导出上机文件在圆机上编织。

本文选取两种不同的花型进行模型的建立及实验编织,编织效果如图15所示,织物的图案清晰且具有一定立体感。图15(a)为两种花卉原始图片,图15(b)为两种花卉对应的意匠图,图15(c)为上机编织出的圆筒状实物图,图15(d)为最终的两款织物实物图,图15(e)左侧图为(d)中左侧花卉的局部花瓣放大图。

图15 从意匠图到织物的实现步骤

4 结 论

本文提出了一种基于三维数据的针织意匠图生成算法。根据花朵的结构特征,建立了基于正投影原理和镜像对称原理的花朵三维模型;通过用户绘制的二维椭圆,对已有模型进行变换处理,生成了多角度的花朵三维模型;最后将三维模型生成图案,转换为提花圆机可用的花型意匠图,并且在提花纬编机上织成了实物。本文提出的算法能够在较短时间内完成对花朵的模型建立,实现意匠图的快速生成和上机使用,提高了工作效率,并且建立的模型可以重复利用,易于产品系列化设计的实现。

《丝绸》官网下载

中国知网下载