基于VIS-NIR 光谱的滨海湿地土壤碳氮比预测建模分析
2023-11-14张清文杨晓芜寇财垚
张清文,杨晓芜,杨 睿,尹 轩,寇财垚
(1.华北理工大学 矿业工程学院,河北 唐山 063210;2.国家知识产权局专利局专利审查协作广东中心,广东 广州 510700)
引言
土壤有机碳(Soil organic carbon,SOC)和土壤全氮(Soil total nitrogen,STN)作为土壤质量和健康的主要指标,在保持土壤质量方面发挥着重要作用[1]。SOC 与STN 的比值(C/N)也是土壤质量和肥力的重要指标,反映了SOC 与STN 之间的相互作用和耦合关系[2]。此外,C/N 是影响土壤微生物群落的主要因素,因此在陆地碳氮循环中起着关键作用[3]。研究土壤C/N 对于土壤管理、生态环境监测和揭示生态系统碳氮耦合关系有重要意义。
传统的化学分析方法测定土壤C/N 需要分别测定土样的SOC 含量和STN 含量,再进行计算C/N,虽然精度较高,但是土壤样品采集劳动强度大,实验室测定人力财力消耗多[4]。近年来,高光谱技术的发展对于快速,低成本且高精度测定土壤各类理化性质提供了新的思路。目前,很多学者已经使用实测高光谱对SOC 含量和STN 含量进行精确的估测[5,6],陈秋实利用实测土壤光谱反射率结合互花米草不同入侵年限探究了互花米草入侵下的滨海湿地SOC 含量,模型决定系数(Coefficient of determination,R2)最高达到0.81[7],卢艳丽对农田耕层土壤的STN 含量进行建模分析,模型R2最高达到0.863[8]。但是将土壤光谱反射率作为自变量,探究土壤的SOC 含量和STN 含量的比值关系相关研究较少。
高光谱数据波段信息丰富,每个波段可以看作是土壤的一种特征,这些特征可以捕捉不同波段下土壤的化学和物理性质,对土壤理化性质的估测有重要意义[9],但波段间反射率信息具有强共线性,即部分波段信息存在冗余。前人多使用Pearson 相关系数确定敏感波段[10],李焱等选取了相关系数最大的10 个波段作为自变量,成功预测了新疆地区不同地表利用类型的STN 含量[11],于雷等比较了全波段与敏感波段建立的预测模型精度,发现敏感波段建立的模型精度略低于全波段建立模型的精度,但全波段模型的复杂度要远高于敏感波段预测模型的复杂度[10]。目前,降维和特征筛选是处理波段间的多重共线性有效方法[12],基于这两种思想,机器学习中的偏最小二乘回归(Partial least square regression,PLSR)和基于决策树的方法得到研究人员广泛重视。
滨海湿地土壤含水量大,可达性差,野外采样难度大。本文基于有限野外采样点的SOC 和STN含量数据和实测高光谱数据,并对原始光谱进行光谱变换以挖掘土壤信息,通过降维和特征筛选的方法确定与土壤C/N 相关的敏感波段,最后基于PLSR 和随机森林回归 (Random forest regression,RFR)建立滨海湿地土壤C/N 的光谱预测模型。以期为湿地碳氮循环提供帮助。
1 材料与方法
1.1 土壤数据采集分析
研究区位于江苏省盐城市大丰区东北部沿海,该地区年降水量为980~1070mm,多集中于夏季,年平均气温在13.7~14.6℃之间[13]。研究区芦苇与碱蓬等本土植物逐渐被外来种互花米草替代,已形成面积广泛的互花米草单一优势植物群落,受互花米草入侵与扩散的影响,原有泥滩逐渐演变为盐沼湿地[14]。本研究考虑到该区范围内互花米草海向入侵特征,垂直于海岸线设计采样方案,每隔40 米进行土壤样本采集,记录每个采样点的经纬度坐标,土壤类型。每个样点处采集3 个表层(0~30cm)土壤样品,充分混合,形成复合样品,共获取33 个土样,样点分布如图1 所示。
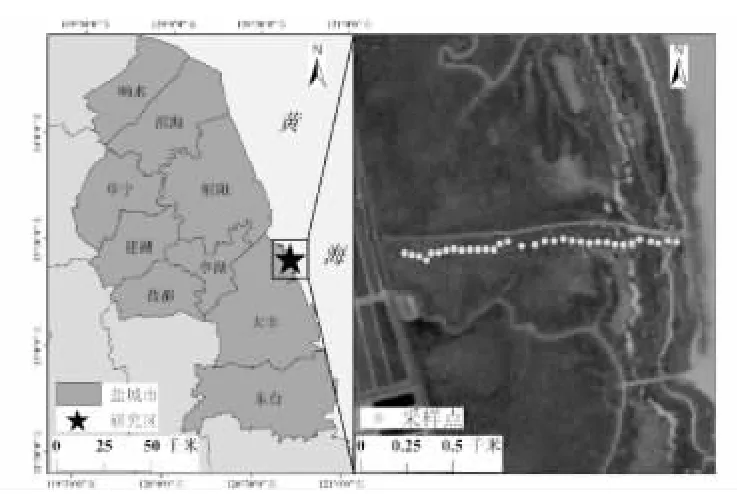
图1 研究区概况图
为减少外界因素对土样的影响,土样室内自然风干,剔除异物,研磨过2mm 筛,分为3 份,分别用于凯氏蒸馏法测定STN 含量[15],稀释热重铬酸钾容量法测定SOC 含量[16],高光谱数据采集。土壤C/N统计特征如表1 所示,数据集偏度为-18.312%,为小偏度数据集且数据分布左偏。

表1 土样C/N 描述性统计
1.2 高光谱测定及预处理
利用ASD FieldSpec 4 便携式地物光谱仪测定土壤光谱反射率,其测量范围是350~2500nm,采样间隔为1.4nm(350~1000nm)和1.1nm(1001~2500 nm),重采样间隔为1nm,共输出2151 个波段。将过筛的土壤样品放置于深2cm,长宽为5cm 的样品盒中,均匀平铺,接触式探头获取该土样的光谱反射率。在每次测量前进行白板校正,以减小光线漫反射影响,每个土样采集10 条光谱曲线,ViewSpecPro计算10 条曲线平均值得到该土样的光谱反射率。
为消除外界环境因素造成的噪声干扰,本研究采用Savitzky-Golay 算法(多项式阶数为2,窗口点数为20)对光谱反射率曲线进行平滑处理。为充分挖掘光谱信息,对平滑后的原始光谱(R)进行数学变换,包括倒数(1/R),对数(LGR),一阶微分(R′)和二阶微分(R")[17,18]。
1.3 数据分析方法
1.3.1 偏最小二乘回归
PLSR 是一种多元回归分析方法,与多元线性回归类似,但不同之处在于PLSR 在建立模型时同时考虑了自变量和因变量之间的关系,即通过构建主成分来最大化自变量和因变量之间的协方差[10]。对原始数据进行正交变换构建的主成分是原始自变量的线性组合,且主成分之间是线性无关的,所以PLSR 适用于处理自变量间多重共线性的数据。PLSR 以提取的主成分代替原始变量参与回归建模,以达到对高维度自变量数据降维的目的[19]。综上,PLSR 可以解决波段间的共线性问题和样本数少于光谱波段数的问题,适用处理高光谱数据。本研究依据留一法(Leave-one-out,LOO)交叉验证计算的预测均方根误差 (Root mean square error of prediction,RMSEP) 确定主成分数量,RMSEP 值随主成分个数的增加先递减,达到最低点后随主成分个数的增加出现微小上升或波动,为防止模型过拟合,提取最小的RMSEP 对应的主成分作为最终建模变量。PLSR 模型使用R 语言中的“pls”包构建。
1.3.2 Boruta 特征筛选
Boruta 特征筛选的内核是随机森林算法。首先Boruta 算法会先根据原始数据集创建一个影子数据集,影子数据集与原始数据集有相同因变量,但每一个自变量被随机打乱,使用两个数据集同时进行随机森林建模,比较模型中的变量重要性,如果同一自变量的重要性在两个模型中有显著差异,则说明此变量为预测土壤C/N 的敏感变量,反之,则为非敏感变量,最后输出所有敏感变量,所有的敏感变量被用于RFR 建模[2]。Boruta 特征筛选使用R语言中的“Boruta”包完成。
1.3.3 随机森林回归
RFR 采用了集成学习的思想,由多个决策树组成,每个决策树是一个弱学习器,通过对这些决策树的集成,随机森林对于高维数据和复杂关系的建模效果良好,能够捕捉非线性、交互作用和噪声[20]。首先随机森林从训练数据集中进行有放回的随机抽样,生成多个不同的训练数据子集。随机森林在每个训练数据子集上随机选择一个特征子集,随机森林对每个训练数据子集和特征子集的组合构建一个决策树。在得到所有决策树之后,对于新的输入数据,每个决策树产生一个预测结果,取所有决策树预测结果平均值,作为最终的模型预测结果。所以RFR 对数据异常值不敏感,具有较高的预测准确性和稳定性。随机森林建模中需要定义两个参数: 每次拆分时随机抽样作为候选特征的数量(mtry)、森林中生成的决策树数量(ntree),RFR 模型基于R 语言的“caret”包使用网格搜索法调整最优参数,采用均方根误差(Root mean square error,RMSE)最小的参数组合构建最终模型。
1.4 精度评价指标
本研究建立模型使用LOO 交叉验证以防止过拟合问题,LOO 交叉验证使用n-1 个样本作为训练集(n 为样本数),没有参与训练的1 个样本作为测试集,几乎用到了所有样本信息,共循环n 次,保证每个样本都被用作测试集,其充分地利用了每个样本,更适用于小样本数据集,验证结果更具代表性。模型的验证指标采用预测值和实测值的R2,RMSE 和平均绝对误差(Mean absolute error,MAE)。R2越接近于1,RMSE 和MAE 越小说明模型精度越高。计算公式为:
2 结果与分析
2.1 不同光谱变换的曲线特征和敏感变量
对R 反射率进行数学变换,各变换后的光谱反射率如图2 所示。各样本R 反射率曲线波形基本相似,在可见光波段(350~780nm)光谱反射率迅速上升,在近红外波段(780~1900nm)上升趋势减缓,在2100nm 处反射率达到峰值,之后平缓下降。在1410nm 和1920nm 处出现明显的水分吸收谷。经过对数变换后,曲线形态与变换前基本一致,但相比于R 反射率曲线,各样本之间的曲线更加聚拢。经倒数变换后的光谱反射率变化趋势与R 反射率曲线完全相反且更加聚集,但曲线趋势发生改变的节点未发生变化。R′反射率反映了原始光谱反射率的增减性,经一阶微分变换后,放大了原始光谱曲线的上升和下降等特征,曲线波动剧烈。二阶微分反映了原始反射率曲线的凹凸性,二阶微分光谱反射率在0 周围浮动。

图2 土样的原始与数学变换后的光谱反射率曲线
通过PCA 确定PLSR 建模使用的主成分个数,选择RMSEP 最小时对应的主成分个数,R,LGR,1/R,R′和R"的主成分个数分别为2,2,2,4 和1。表明经简单数学变换(LGR,1/R),主成分个数未曾发生变化,经过一阶微分后,主成分个数提高为4 个,表明原始光谱中一些微弱的变化,在经微分后得到更强烈的信号,导致主成分分析时提取更多的主成分来解释这些变化,即一阶微分变换挖掘出了更多土壤信息。二阶微分反射率在0 周围浮动,且浮动幅度类似,仅一个主成分即可概括绝大多数自变量信息。
Boruta 特征选择筛选出用于RFR 建模的变量如表2 所示,R 和LGR 筛选出的特征波段除2450 nm 和2486nm 外完全一致,说明R 进行对数变换对识别敏感波段并未有明显改善。进行倒数变换后,敏感波段从19 个增加至39 个,敏感波段所处的波段范围基本一致,均集中在1900~2500nm。经一阶微分变换后,敏感波段的数量从21 个提升至38 个,二阶微分后,筛选出的敏感波段数量减少到15 个。微分变换后,敏感波段的位置发生较大改变,由未变换前短波红外范围扩散至可见光范围,短波红外范围的敏感波段减少,且分布较分散,说明经过微分变换凸显了可见光范围的光谱特征,挖掘出更多可见光波段的光谱信息。
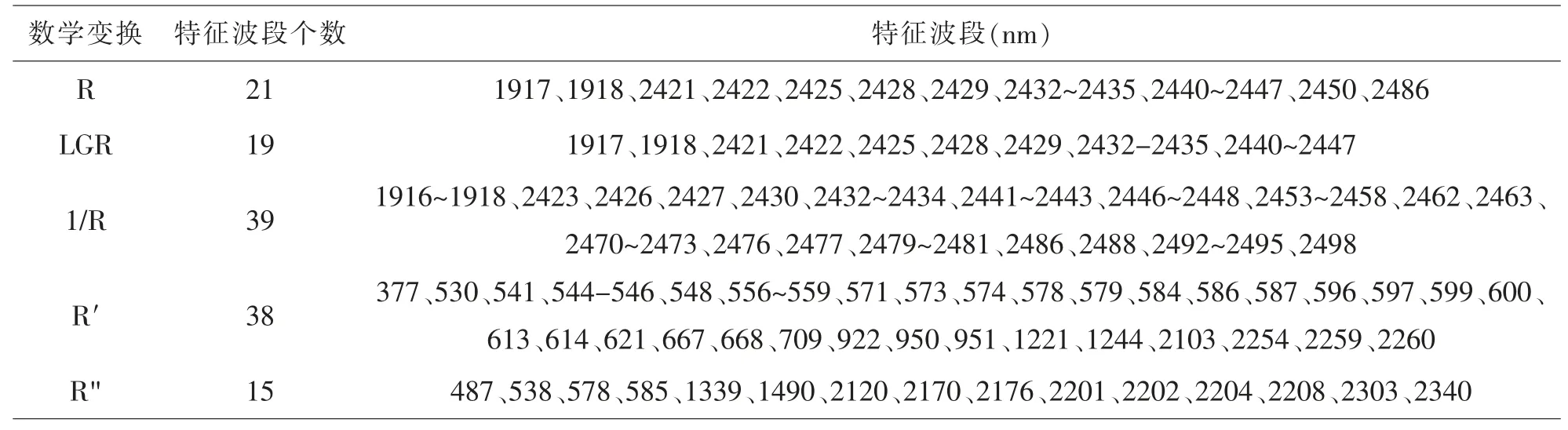
表2 Boruta 筛选的敏感波段数量及位置
2.2 模型对比分析
结合PLSR,RFR 和不同光谱变换的波段反射率构建的土壤C/N 预测模型评价指标如表3 所示,不同模型和不同变换形式对模型精度有显著影响。两种机器学习算法中,未经微分变换(R,LGR 和1/R)的光谱反射率建立的模型有相似精度,PLSR 模型 中R,LGR 和1/R 的R2分 别 为0.698,0.697 和0.694。表明经对数和倒数变换的光谱反射率对预测模型精度没有显著提升,甚至模型精度有轻微降低,RFR 模型中也发现相同规律。经微分变换的光谱反射率建立的模型精度得到提高,PLSR 中,相比于R 建立的预测模型,R′,R" 建立的预测模型R2分别提升了42.6%和33.0%,RFR 中,相比于R 建立的预测模型,R′,R"建立的预测模型R2分别提升了42.9%和42.0%,表明一阶微分能挖掘潜在的土壤信息,一定程度上消除噪声,提高预测模型精度,提高幅度相似证明PLSR 中的主成分提取和Boruta 筛选效果相似。
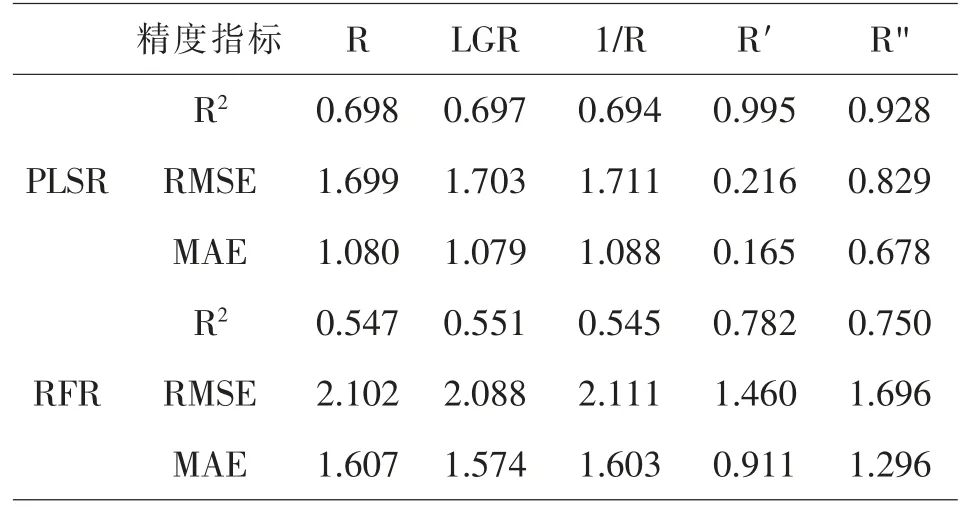
表3 土壤C/N 不同模型精度对比
对比PLSR 和RFR 模型,PLSR 建立的预测模型精度高于RFR 模型,PLSR 通过提取的主成分解释波段与C/N 的线性关系,而RFR 对非线性关系有更强的解释能力,PLSR 算法相比于RFR 算法更适用于建立高光谱数据与土壤C/N 之间的关系。R及其4 种变换后的光谱反射率建立的PLSR 模型比RFR 模型有不同程度地提高,R2提高23.7~27.6%,即每种变换的提高幅度差异较小。预测结果与实测值之间散点图如图3 所示,表明预测值与实测值之间有很好的相关性,预测结果是可靠的,PLSR 模型的预测值与实测值的拟合直线相比与RFR 模型的拟合直线更接近于1:1 线,表明PLSR模型预测效果比RFR 模型更好。
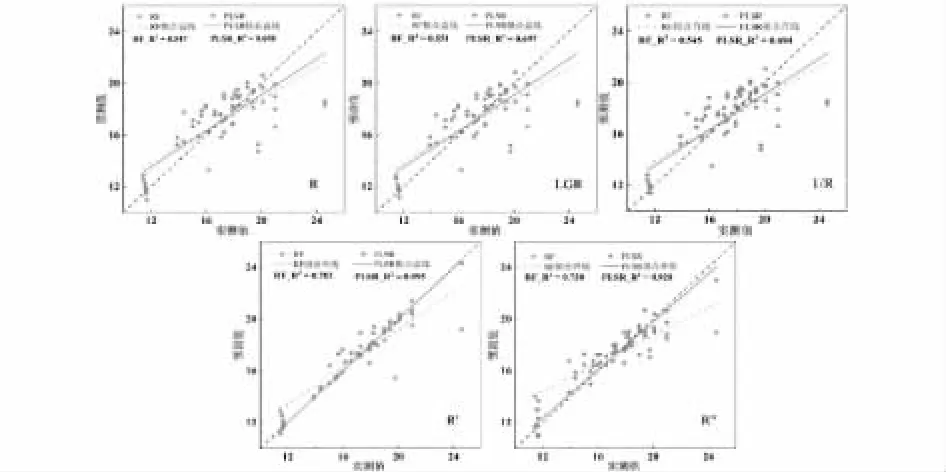
图3 不同光谱变换和不同建模方法预测的土壤C/N与实测值比较
3 结论
高光谱技术依靠其数据获取快捷,波段信息丰富等优势被广泛应用于估测土壤理化性质,但野外环境复杂,受到土壤水分、土壤杂质和大气条件等影响,背景噪声大,采集土样实验室内测定高光谱数据可以获得较为稳定的光谱信息,结果相对理想,相比复杂的化学测定土壤C/N 方法,又省时省力无污染。本研究通过对土样高光谱曲线的重采样、平均和平滑预处理,并对原始光谱反射率曲线进行4 种数学变换,使用主成分分析、Boruta 特征筛选、PLSR 和RFR 对土壤C/N 分析研究,得到的具体结论如下:
(1)原始光谱R,对数变换LGR 和倒数变换1/R,Boruta 筛选出的敏感波段范围相似,集中在1900~2500nm,微分变换后筛选出的敏感波段均匀分布在整个波段区间,微分变换能有效挖掘光谱信息。
(2)在PLSR 和RFR 模型中,对R 进行对数和倒数变换并不能提高模型精度,对R 进行微分变换,在两种算法建立的模型精度均得到了显著提高,R2最高提升42.9%。
(3)两种算法均能有效预测土壤C/N,PLSR 模型精度比RFR 模型精度高23.7~27.6%,PLSR 更适用于小样本数据集建模预测,基于PLSR 和R’构建 的 最 优 模 型,R2为0.995,RMSE 为0.216,MAE为0.165。
