一种适应火星主要地形的航天器仿生足设计

徐杰 徐雄 左堃罡 夏善涛 许可

(上海航天电子技术研究所,上海 201109)

随着航天科技的发展,火星吸引了全球范围内越来越密切的关注,多种火星着陆器和火星车开展了多项火星探测任务。从1996年至2021年,NASA已成功发射了探路者号、机遇号、好奇号、毅力号等火星探测器[1-3],中国的祝融号火星车也于2021年5月15日成功着陆火星[4]。这些探测器目前主要采用轮式火星车的形式,可在较为平坦的地形中行驶探测。然而,火星上火山运动明显,地形主要以细软的沙漠和陡峭的山地为主,广泛分布山峰、陨石坑、河道、沙漠[5]。轮式火星车出现过在沙漠中沉陷的现象,也难以在较为陡峭的山地中行驶,探测范围具有较大的局限性。

目前,在火星探测器新型运动方式方面已经开展了一些研究。例如:NASA的毅力号探测器携带了一架火星直升机[6],以扩大其任务探测范围;还有机构在研究足式火星机器人[7-9],其具备灵活的运动模式,若配备合适的足部可将探测范围扩展至一定的山地中。自然界中,有些动物的足部具备可用来爬树或爬墙的尖爪,给机器人足部附加类似特殊机构可使其具备攀爬大倾角壁面的能力,文献[10-12]中开展了相关研究。然而,以上研究皆专注于提升机器人在崎岖环境中的运动能力,未兼顾在沙漠等平坦、松软地形上的运动能力,对火星地形不够适配。为了兼顾火星上松软沙地和崎岖山地2种地形,本文设计一种新型仿生足,其具备多弧形的大底面,并搭载仿生钩爪。在相同条件下,多弧形底面足垫可与底面产生较大的摩擦力和支持力,在沙漠中具有稳定高效的运动性能。钩爪可以在粗糙壁面产生有效的抓附力,使足式火星机器人具备山地越野能力。仿生足用于足式火星机器人可以克服传统火星车难以行至火星沙漠和山地的缺陷,拓展探测范围;还可用于火星着陆器,提升其着陆的稳定性并防止其卡陷于柔软沙地。因此,本文设计的仿生足具有航天实用前景。

1 仿生足设计

仿生足结构包括上部刚性垫、下部柔性垫和仿生爪3个部分,如图1所示。刚性垫可用来连接机器人腿或着陆器腿,并且使用扭转弹簧限制运动范围。柔性垫采用多弧形底面设计,当探测器与地面接触时,可以起到缓冲作用。当安装在机器人上时,柔性垫可以在沙地上发挥更好的防滑和防下沉作用。搭载仿生足的足式火星机器人的单腿运动如图2所示。考虑到机器人的脚后跟首先接触地面,柔性垫在脚后跟部分长于刚性垫。钩爪可以固定安装,也可以通过绳索驱动和弹簧限位进行运动。实际运动模式可以根据抓附和越野需求进行定制。

图2 足式火星机器人运动时腿部动作Fig.2 Leg action of legged Mars robot in motion

足部四周理论上都可以安装钩爪,可根据不同工况进行选择。搭载于着陆器时可使用3面(外沿+前沿+后沿)或4面,搭载于留足机器人时可使用1面或2面(外沿或外沿+前沿)。结合图2的机器人腿部落脚运动过程可知,接触地面时足部在下降的同时做内扣和后移运动。前沿钩爪相对地面将产生往后的运动趋势,外沿钩爪将产生往内的运动趋势,因此利于钩爪在粗糙壁面上产生抓附。同理,当足部完成落脚运动后进行抬脚运动时,足部在抬升的同时做外扩和前移运动,钩爪将沿原来的抓附方向原路撤出,达到自然脱附的效果。这种设计可以在一定程度上避免钩爪卡陷的问题,若仍有特殊情形造成钩爪卡陷,可通过绳索主动驱动钩爪抬升以帮助其脱困。

2 仿生足力学分析

2.1 沙地中的运动受力分析

为了探索仿生足的多弧形柔性底面的防滑和抗沉陷性能,对运动中的传统圆轮与多弧形底面柔性足垫建立与地面的相互作用模型,并分析对比。在外界物体的作用下,火星土壤会产生沉降变形,包括弹性变形和塑性变形。根据车辆-地面力学理论[13-14],在贝克(Bekker)承载模型的基础上,采用适用于塑性土壤的杰诺西(Janosi)剪切模型和适用于脆性土壤的王氏(Wong)剪切模型[15-16],对耦合系统进行分析和求解。

柔性轮与地面接触时,车轮会部分变形并与地面贴合,车轮与土壤之间的接触面可近似看作1个平面和1个弧形面的组合,模型如图3所示。接触面属于平面中的一部分时,剪切力的法向分量为0,因此柔性轮受到地面的法向作用力FN1和切向驱动作用力FT1为

注:FZ为载重;R为圆轮半径;z0为最低处沉陷量;a和b为水平接触面的2个端点;b和c为弧形接触面的2个端点;θ为接触点与轮心的圆心角。图3 圆轮-土壤接触模型Fig.3 Contact model of wheel with ground

(1)

式中:B为车轮宽度;法向应力p(θ)见式(2);切向应力τ(θ)见式(3)。

(2)

式中:ksc为土壤粘聚变形模量;b为轮接地边长;ksf为土壤内摩擦因数;n为沉陷指数。

(3)

式中:p′为土壤内聚力;φ为土壤内摩擦角;j为剪切位移;k为剪切系数。

仿生足的多弧形柔性足垫截面呈6个圆弧,其运动工况如图4所示。为控制变量,设此模型中的圆弧半径R′与图3中圆轮半径大小关系为6R′=R。

注:FZ1～FZ6为各弧形垫的载重;R′为各弧形垫半径;θ1～θ6为各弧形垫接触点与轮心的圆心角,p1～p6为各弧形垫受到的法向应力。图4 多弧形柔性足垫运动工况Fig.4 Movement conditions of multi-arc flexible foot soles

根据式(1)推理可知,多弧形柔性足垫受到地面的法向作用力FN2和切向驱动力FT2为

(4)

式中:p(θi)见式(5)。

(5)

将各个半圆形接触的土壤状况近似为相同,可得FN2为

(6)

由于6R′=R,当沉陷相同深度时,FN2可表示为

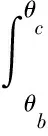
(7)

因此,当载荷相同时,多弧形柔性足垫的沉陷量将小于柔性轮,多弧形柔性足垫抗沉陷性能更佳。同理,FT2为

(8)

因为6R′=R,FT2可表示为

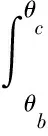
(9)

因此,在相同条件下,多弧形柔性垫所受切向牵引力大于传统圆轮,且多弧形柔性垫的防滑性能更佳。

综上可知:在松软地面中运动时,多弧形柔性足垫的防滑与防沉陷性能优于传统圆轮。

2.2 钩爪在粗糙面上作用的力学模型

为探究仿生钩爪的性能规律并提升仿生足对火星地形的适应性,根据火星崎岖山地的特点,建立钩爪作用于倾角0°～90°以内的任意粗糙面的球接触模型。接触模型近似可以设定为钩爪尖端的假想圆和粗糙壁面颗粒的假想圆之间的接触。粗糙壁面包括粗糙颗粒及其固定的基底构成,将固定基底适当简化为平整面[17-18]。

依据钩爪尖端是否接触到粗糙颗粒的固定基底,钩爪的工作状态可分为2种情况。当粗糙壁面的倾角较小时,钩爪一定会受到壁面的支持力,此时机器人容易爬上壁面。当粗糙壁面倾角较大时,机器人重心位于钩爪与壁面接触点以外,机器人将有后仰的趋势,此时钩爪不会受到壁面的支持力,机器人能否爬上壁面的关键在于钩爪能否产生足够的抓附力。建立该状态下钩爪与粗糙斜面的球接触模型,见图5(a);图5(b)为几何关系。定义机器人机身对钩爪尖端的作用力F与重力方向的夹角为载荷角ω;α为钩爪尖端圆心与粗糙颗粒圆心的连线与竖直方向的夹角,其为钩爪与粗糙颗粒的接触角,受钩爪尖端直径(2r,r为半径)、粗糙颗粒直径(2Rp,Rp为半径)影响;μ为最大静摩擦系数。根据受力平衡条件可知;当摩擦力f>Fsin(ω-α)时,钩爪可以稳定抓附;否则,钩爪会发生滑落。N为粗糙颗粒作用于钩爪尖端的支持力,由于f=μN,N=Fcos(ω-α),根据图5(b)中的数学关系可得

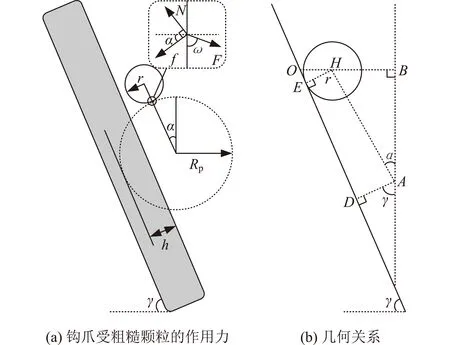
图5 钩爪纵向作用于粗糙斜面的球接触模型Fig.5 Ball contact model of bionic claw acting on rough wall

(10)

式中:h为粗糙颗粒在基底中的没入深度;γ为斜面倾角。

因此可得

(11)

rmax/Rp是钩爪尖端最大半径与粗糙颗粒半径的比值。根据式(11)可以看出:当钩爪产生有效附着时,rmax/Rp与h,ω,γ,μ有关。为简化变量,将γ设为45°,分析其他3个变量对rmax/Rp的影响。将μ设为协变参量,绘制μ为0.2,0.4,0.6,0.8时钩爪附着于粗糙斜面时其尖端尺寸r/Rp与h,ω的关系图,如图6所示。由图6中可以看出:当μ不变时,h和ω越小,rmax/Rp越大,即保证实现抓附条件下允许的钩爪尖端半径rmax/Rp越大,这表明产生有效抓附的条件越低时,抓附性能越好。当h与ω一定时,r/Rp小于rmax/Rp时(即图6中位于曲面下方的部分),钩爪均可以实现有效抓附。当μ不同、其他参数相同时,μ越大,曲面的r/Rp越高,即rmax/Rp越大,满足附着要求下钩爪尖端半径可以更大,这表明斜面粗糙度越高,钩爪抓附性能越好。

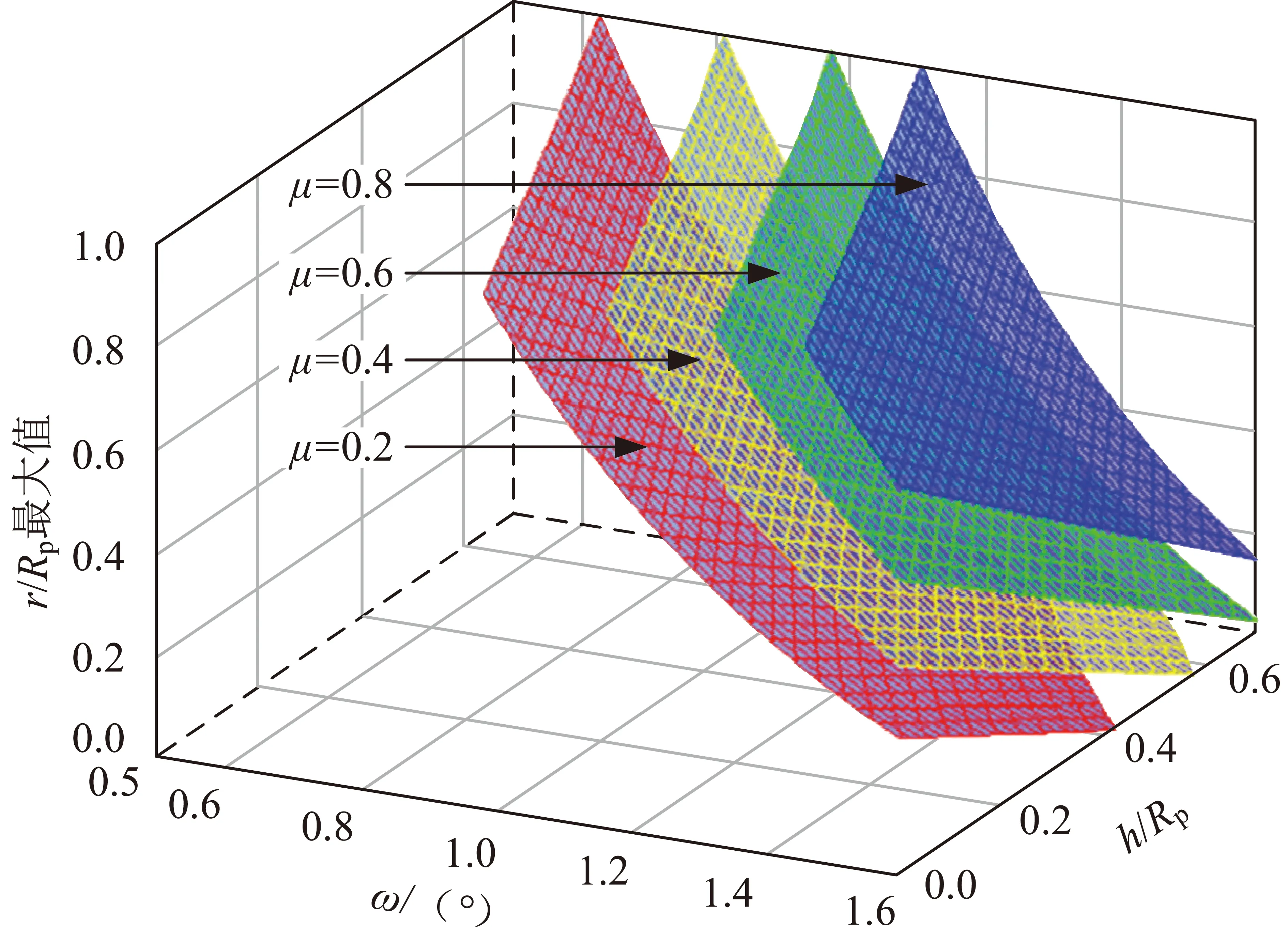
图6 不同μ时下钩爪尖端尺寸r/Rp与粗糙颗粒埋入深度h、载荷角ω的关系Fig.6 Relationship among r/Rp, h and ω under different μ

3 仿生足抓附性能研究试验

为更好地实现火星机器人足部钩爪的越障功能,使用针灸针制作钩爪,通过3D打印使用尼龙材料制作尺寸为555mm×415mm×250mm的仿生足和六足机器人部分腿部实物。在确定钩爪安装基底的前提下对钩爪数量和钩爪抓附角2个参数设计多组对照试验,寻求抓附性能最优化的钩爪的参数。

粗糙壁面可使用石英砂颗粒与平板仿制而成,石英砂的目数与其筛孔直径之间的关系如表1所示。根据火星粗糙壁面特征,选用目数为10的石英砂颗粒粘于木板表面,制成粗糙壁面用于机器人足部进行钩爪抓附试验。粗糙板固定在力传感器上,该传感器可以实时检测水平力和垂直力。最终搭建的抓附力测试平台如图7所示。将仿生足通过腿部安装到2维移动平台上,以安装位置为原点O建立坐标系,仿生足上下(Y轴方向)和前后(X轴方向)运动可由程序精确控制。

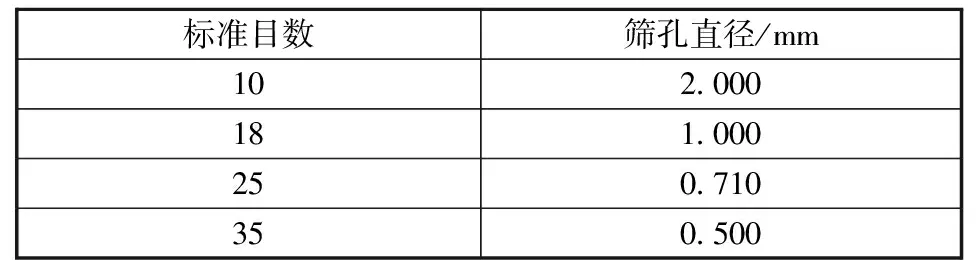
表1 石英砂目数与其筛孔直径关系Table 1 Relationship between mesh numbers of quartz sand and diameter of sieve holes

试验中仿生足运动过程如图8所示。在每组试验中,首先进行Y轴方向的按压运动,直到Y轴方向上的预压力相等。各组的预压均保持在7N。在这个过程中,只有钩爪与粗糙板接触,足垫保持不接触。将钩爪朝向分别以沿X轴方向(夹角为0°)、与X轴方向夹角为30°、与X轴方向夹角为60°设置3个方向的试验。在X轴方向上以20mm/s的恒定速度移动足部100mm,收集粗糙板在X轴方向的受力变化。力传感器设置为每秒收集100组数据。

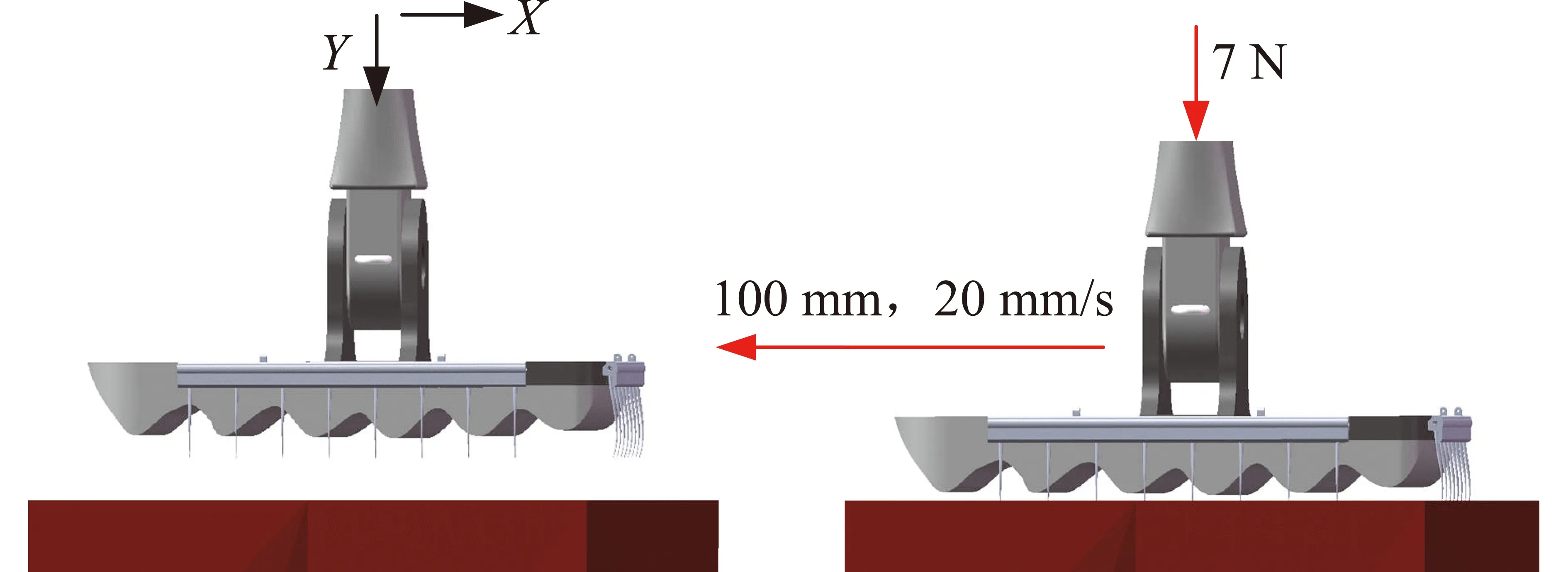
图8 试验中足部的运动过程Fig.8 Foot movement in tests

3.1 最佳钩爪目数研究

为研究仿生足单个方向上安装的钩爪目数对足部抓附力的影响,控制其他条件相同,制备如图9所示的5组钩爪进行3个朝向上的试验,钩爪弯曲角均为115°。在每个朝向上每组试验重复3次,同一朝向上每组钩爪在重复试验中表现较为一致,3个朝向上5组试验中粗糙板受到的X轴方向的力FX(即抓附力)变化情况如图10所示。图10中,红、绿、蓝、黄、黑曲线依次对应目数为4,5,6,7,8的钩爪。

图9 5组不同目数的钩爪Fig.9 Five sets of claws with different mesh numbers

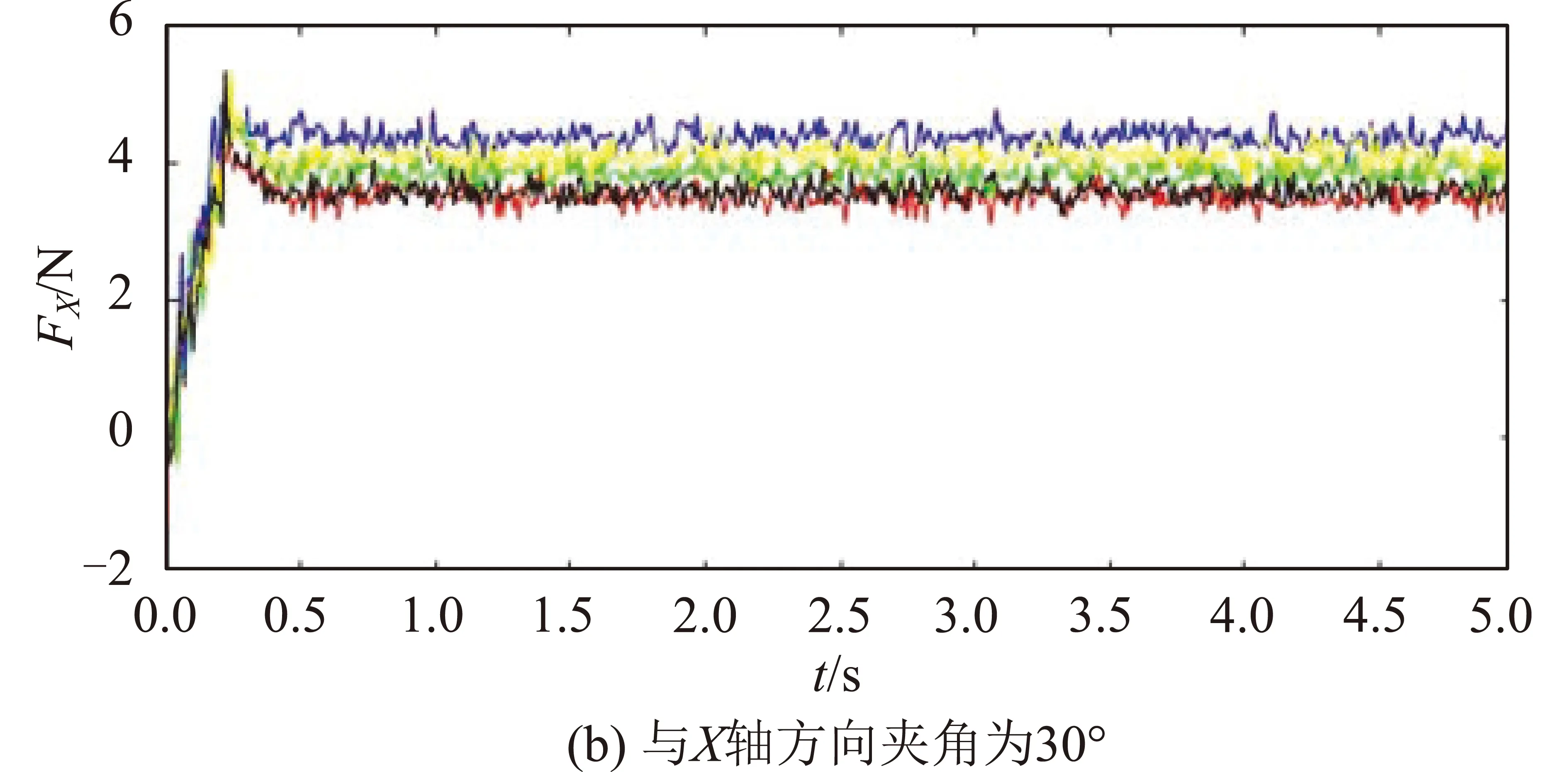
观察图10中曲线可知:在预压力作用下,随着足部在X轴方向上产生位移,钩爪逐渐产生抓附力。抓附力在短时间内(约0.3s后)达到峰值,随后略微下降至稳定值。达到峰值时,钩爪与粗糙面建立最大静态抓附;达到稳定值时,钩爪与粗糙面建立较为稳定的动态抓附。汇总各组试验的动态稳定抓附力平均值,如表2所示。由表2内数据可知:在每个朝向上的5组试验中,稳定抓附力最大的皆为目数为6的钩爪,这表明装有目数为6的钩爪的仿生足抓附性能最好。对比3个朝向的每组试验数据可知:随着钩爪朝向与X轴方向夹角变大,试验中产生的稳定抓附力变小,这表明钩爪沿其朝向对粗糙面抓附时效果最佳。

表2 3个钩爪朝向上不同目数钩爪产生的稳定抓附力Table 2 Stable gripping forces of crawls with different numbers in 3 directions N

3.2 最佳钩爪弯曲角研究

为研究钩爪弯曲角对仿生足抓附力的影响,控制其他条件相同,利用第3.1节试验结果,将钩爪目数定为6。制备钩爪弯曲角分别为95°,105°,115°,125°,135°的5组钩爪进行3个朝向上的试验,如图11所示。第3.1节已经做过钩爪弯曲角度为115°的试验,依然保持每组试验的预压力均为7N,另做4组对比试验。

图11 5组不同角度的钩爪Fig.11 Five sets of claws with different bending angles

同一朝向上的每组钩爪在重复试验中表现较为一致,3个朝向上4组试验中粗糙板受到的抓附力变化情况如图12所示。图12中:红、绿、蓝、黑曲线依次对应目数为4,5,7,8的钩爪,曲线规律与第3.1节相同,汇总各组试验的动态稳定抓附力平均值如表3所示。由表3中数据可知:在每个朝向上的4组试验中,稳定抓附力最大的皆为弯曲角度为125°的钩爪,产生的抓附力依然随着钩爪朝向与X轴方向夹角变大而变小。

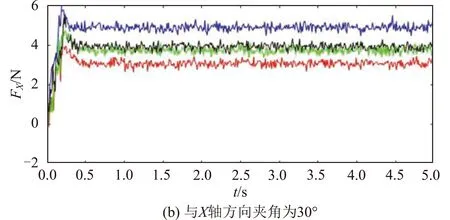
图12 不同弯曲角度钩爪的抓附力曲线Fig.12 Gripping force curves with different bending angles of crawls

总结本节研究结果可得:当仿生足搭载于足式火星机器人上时,其钩爪的最佳设计方案为安装目数为6、弯曲角度为125°。

4 仿生足应用于火星探测器

图13提供了可搭载仿生足的六足火星机器人和着陆器模型。火星机器人每条腿有3个自由度,能以丰富的步态灵活运动。其身体还搭载了机械臂、可折叠太阳能板和各种探测仪器。利用仿生足,该火星机器人可以在更多的沙漠和山地中运动并执行探测任务。着陆器4条支腿装有减震弹簧等部件,并搭载火星机器人和其他仪器。利用仿生足,着陆器的降落过程可以得到更好的缓冲,落地后也可以更稳定的固定在地面。

图13 搭载仿生足的六足火星机器人和着陆器模型Fig.13 Model of hexapod Mars robot and lander with bionic feet

为了进一步验证仿生足可提升火星机器人运动稳定性和越障性能,建立崎岖地形模型,将柔性垫模型柔性化处理,并使用运动仿真软件对机器人开展刚柔耦合运动仿真,如图14所示。机器人运动性能良好,可以翻越崎岖的地形模型。仿真过程中还得到了柔性足垫脚尖和脚跟接触地形时产生的实时适应性形变曲线。最终结果表明:仿生足的柔性足垫和钩爪达到了预期的减震和抓附效果。

5 结束语

本文以火星探测为背景,设计了一种仿生足。以火星广袤的沙漠和山地地形为切入点,设计了多弧形柔性足垫和装在足垫周边的仿生钩爪。足式火星机器人可搭载此仿生足,进入更广阔的火星地形中执行探测任务。火星着陆器也可搭载此仿生足,以增加降落和停放的稳定性。对多弧形足垫和仿生钩爪的力学分析、仿真试验及实物试验,验证了仿生足的优越性能并得到了最佳钩爪配置。以上研究结果可为未来的火星探测任务提供一些新的思路和方向。