不同地表粗糙度坡面流水力学特性试验研究

2023-11-13张旖璇薛梦华王福星李浩玉宋天翼

陕西师范大学学报（自然科学版） 2023年6期

张旖璇,马岚,2,3*,薛梦华,孙旭,王福星,李浩玉,宋天翼

(1 北京林业大学水土保持学院首都圈森林生态系统国家定位观测研究站,北京 100083;2 北京林业大学国家林业和草原局水土保持重点实验室,北京 100083;3 北京林业大学山西吉县森林生态系统国家野外科学观测研究站, 北京 100083)

坡面流是降水经植被截留、地表填洼、土壤入渗后,在重力作用下沿坡面运动的浅薄水流。与一般的明渠水流不同,坡面流是一种动态流向的薄层水流,水深通常只有几毫米甚至为零点几毫米,由于径流沿程不断汇入质量源和动量源,其随空间和时间变化较大,这使坡面流测定有一定难度[1-2]。坡面流是土壤分离和泥沙输移的主要动力,其水动力学特性对土壤侵蚀影响显著[3-6]。有关坡面流水动力学特性的研究,是构建土壤侵蚀物理模型的基础[7],有助于对坡面侵蚀机理的理解和合理防治措施的制定。坡面流流经的地表一般粗糙不平,随着地表粗糙程度的不同,坡面流表现出不同的特性。流速、水深、流型、流态、阻力系数等水力学特征参数是表征坡面流的常用指标,其均受粗糙度因子的影响[8-11]。

近年来,学者们探究了坡面流流速、水深及阻力系数等水力学特性参数受粗糙度的影响,取得了很大进展。但粗糙度颗粒粒径范围设置差别较大,均匀性和连续性的设置各不相同[8-10,12-13],故所得结论存在差异。前人多采用间接计算方法得到阻力系数或径流剪应力,并对其与坡度和下垫面因子的关系进行探究[14-16],由于试验条件所限,直接测定技术没有得到推广应用[17]。本研究对直接测定技术进行尝试与探索,为更加快捷获取径流剪应力提供一种新的研究手段和方法。

因此,本研究利用室内定床冲刷试验,通过布设不同粗糙度下垫面,在不同坡度和流量下开展系统研究,并通过径流剪应力直接测定设备,探究坡面流水力学特性参数和径流剪应力随流量和坡度的变化规律,为进一步探究坡面水文过程奠定基础,为从水动力学角度进行水文侵蚀机理的阐述和侵蚀物理模型的构建提供依据,为指导水土保持坡面整治措施的合理选择提供理论支持。

1 材料与方法

1.1 试验设计

自然界中坡面薄层水流多为动床非恒定沿程变量流,为了较为精准地对坡面流进行观测和定量描述,本研究采用室内定床冲刷试验,消除土壤、植被等因素的干扰,模拟研究不同粗糙度、不同坡度、不同流量下坡面流水力学特征和径流剪应力特征。

1.1.1 试验装置

试验于2021年5～9月在北京林业大学鹫峰人工模拟降雨实验室进行,采用的自制装置(图1)由供水系统、流量控制系统、稳流箱、平水设施、试验水槽、拉力传感器6部分组成,其中水槽长2.1 m、宽0.6 m、深0.15 m,坡度可调范围为0°～15°。

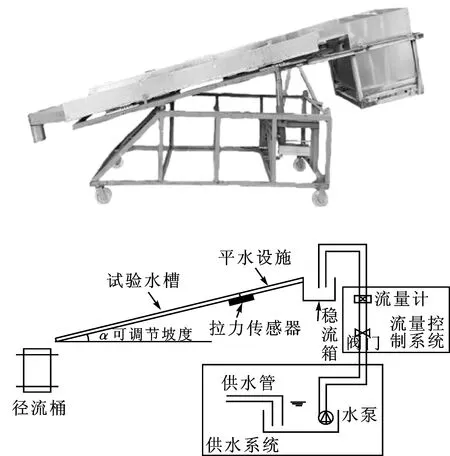
图1 试验装置Fig.1 Experimental device

1.1.2 试验设置

本研究将不铺设砂粒的光滑泡沫板(相当于0 mm粒径)床面作为对照组,设置5种人工模拟粗糙床面。将石英砂人工过筛,使砂粒粒径范围分别为0.2～0.6 mm、0.6～1 mm、1～1.4 mm、1.4～2 mm、2～3 mm。在床面上均匀平整地涂抹一层清漆,保证砂粒可以牢固粘在床面上;将某一粒径范围的砂粒均匀地分散在床面上,以形成具有突起的相对均匀的下垫面粗糙度;最后再涂抹一层清漆包裹住砂粒,使其更加牢固。设置3种坡度,分别为3°、9°和15°。依据自然界实际情况,并参考已有研究[15,18],设置10组流量,分别为0.15、0.30、0.45、0.60、0.75、0.90、1.05、1.20、1.35和1.50 L/s。

1.2 测定方法

按水流方向,将水槽坡面从上到下均匀地划分成3个坡段,每个坡段长0.7 m。在每个观测坡段按横向平均取左、中、右3个测点,整个坡面共9个测点,进行水深和流速的测定,见图2。水深采用精度为0.01 mm的水位测针测定,9个测点平均值作为该工况下水深值。采用高锰酸钾染色剂示踪法测定表面流速,3个坡段分别按左、中、右测定,每个流速测定3次取中间值,取9个流速的平均值作为该工况下的表面流速。温度采用精度为0.1 ℃的水银温度计测量,于每场试验开始和结束时各记录一次,取平均值。

图2 测点布设Fig.2 Measuring point layout

径流剪切力由自制测定装置测定,采用S型拉力传感器,传感器布设在试验水槽下方,连接上半部分水箱和下半部分坡面(图1)。其原理是内部的弹性元件在外力作用下产生弹性变形,使其表面粘贴的电阻应变片也产生变形,电阻应变片在变形下阻值发生改变,经过测量电路将其转化为电信号。水流流动时,在径流剪应力作用下会使坡面产生整体位移变化,进而使传感器受到的拉力产生变形并转化为电信号,产生的电信号变化被数显计显示并记录。试验开始前先将稳流箱注满水,之后关闭电磁流量计,将数显计与S型拉力传感器相接,待床面不再有水流动时,将数显计置零;之后调节至各试验流量,待数显计读数稳定后,该数值即为当前流量下的径流剪切力。

1.3 试验参数计算

除试验中测量得到的表面流速v表面、水深h及温度t,本研究涉及计算的主要水力学参数包括坡面流平均流速、雷诺数、弗劳德数、阻力系数和径流剪应力。

1.3.1 平均流速

高锰酸钾染色剂示踪法所测流速为坡面流表面流速,采用Abrahams的修正方法[19]修正系数α(层流为0.67、紊流为0.8、过渡流为0.7)。平均流速(v)等于表面流速乘以修正系数,计算公式为

v=αv表面。

(1)

式中:α为修正系数;v表面为试验测得的坡面流表面流速。

1.3.2 雷诺数

无量纲参数雷诺数(Re)是判别水流流态的核心参数,它是水流惯性力和黏性力的比值。Re越大,水流惯性力越大,水流发生紊动的可能性也就越大;Re<575为层流,575≤Re≤6 500为过渡流,Re>6 500为紊流。计算公式为

(2)

式中:R为水力半径(m),薄层水流水力半径近似等于断面平均水深h;η为水流黏滞系数(m2/s),其计算公式为

(3)

式中t为水温(℃)。

1.3.3 弗劳德数

弗劳德数(Fr)反映水流的惯性力和重力之比。当Fr=1时,水流为临界流;当Fr>1时,水流为急流;当Fr<1时,水流为缓流。计算公式为

(4)

式中g为重力加速度(m/s2)。

1.3.4 阻力系数

Darcy-Weisbach阻力系数f反映水流阻力,即下垫面对流动水体的阻力大小,计算公式为

(5)

式中:J为水流能坡,J=sinθ,θ为水槽坡度(°)。

1.3.5 平均粒径

为了更好地探究粗糙度因子对坡面流流速的影响,用砂粒平均粒径d表示床面绝对粗糙度[9, 20],计算公式为

(6)

式中dmax和dmin分别为床面铺设砂粒的最大粒径(mm)和最小粒径(mm)。

1.3.6 计算径流剪应力

计算径流剪应力为通过公式计算得到的径流剪应力,计算公式为

τ=ρgRJ,

(7)

式中ρ为水密度(kg/m3)。

1.3.7 实测径流剪应力

实测径流剪应力F由传感器直接测量的径流剪切力除以下垫面面积得到,计算公式为

(8)

式中:F剪切力为传感器测量值(N);A为下垫面面积(m2)。

2 结果与讨论

2.1 坡面流流速

坡面流流速是研究坡面侵蚀过程和侵蚀机理的重要参数,可以较为直观和整体地反映坡面流状况。由图3可知,粗糙度一定时,坡面流流速在3种坡度下均随流量的增大而增大;流量一定时,流速总体随粗糙度的增加而减小,且光滑下垫面的流速明显大于粗糙下垫面,5种不同粗糙度床面的流速由大到小依次为0.2～0.6 mm、0.6～1 mm、1～1.4 mm、1.4～2 mm、2～3 mm。地表粗糙度增加对水流流速的抑制作用明显,其原因是水流在颗粒凸起的阻碍下克服阻力做功,产生能量损失,且粗糙度越大,绕流阻力越大,水流能量损失也越大,从而有效降低了坡面流的动能和侵蚀力[9]。

图3 不同坡度和粗糙度下坡面流平均流速Fig.3 Average velocity of overland flow under different slopes and roughness

不同粗糙度下,对流速与流量、坡度进行相关性分析,三者间呈幂函数关系。参照传统水力学流速、坡度因子的幂函数公式v=kQmSn(式中:v为平均流速(m/s);k为随坡面表面特征而变化的系数;Q为流量(L/s);S为坡度的正弦值),对不同粗糙度下垫面坡面流流速进行多元回归分析,结果见表1。

表1 不同粗糙度下流速与流量、坡度回归关系Tab.1 Regression relationship between velocity, flow and slope under different roughness

由表1可知,所有回归方程的决定系数均大于0.98;k值范围为0.522～1.284,随着下垫面粗糙度的增加逐渐减小;指数m的变化范围为0.241～0.347;指数n的变化范围为0.317～0.557,且随着粗糙度的增加而增加,说明随着粗糙度的增加,坡度对流速的影响逐渐变大。同时,除对照组试验条件外,所有回归关系中n值均大于m值,说明相较流量,坡度因子对有粗糙度覆盖床面的坡面流流速影响更大。

将v与流量因子Q、坡度因子S、粗糙度因子d进行多元回归分析,得到幂函数回归方程

v=0.682Q0.419S0.291d-0.140,R2=0.976。

方程决定系数较高,进一步说明坡面流流速可以用流量、坡度和粗糙度3个影响因子进行良好表达。这与前人研究结果相似,即流速随流量增加呈幂指数增加趋势[13]。本研究将坡度因子和粗糙度因子共同拟合至方程中,结果更加完善。

试验结果也为坡面水土保持措施布设提供了一种思路,即在一定范围内选择相对较大的土壤粒径,从而形成较粗糙下垫面,以更好地减缓坡面流流速并减弱土壤侵蚀。未来可在宏观尺度上延伸至设置地表起垄、增加地表覆盖度等方式以增加地表粗糙度,为水土保持生产实践措施提供更多方法与建议。

2.2 坡面流水深

水深与流量、粗糙度在3种坡度下的关系见图4。在粗糙度相同时,水深随流量增大而增大;流量一定时,大部分坡面流水深随粗糙度的增加而增大。本研究设计为定床下垫面,几乎没有水分下渗造成的损失,水深的理论计算方法为单宽流量除以流速,可知单宽流量不变时,流速的减小必然会造成水深的增加,试验结果与施明新等[9]研究结果相似。

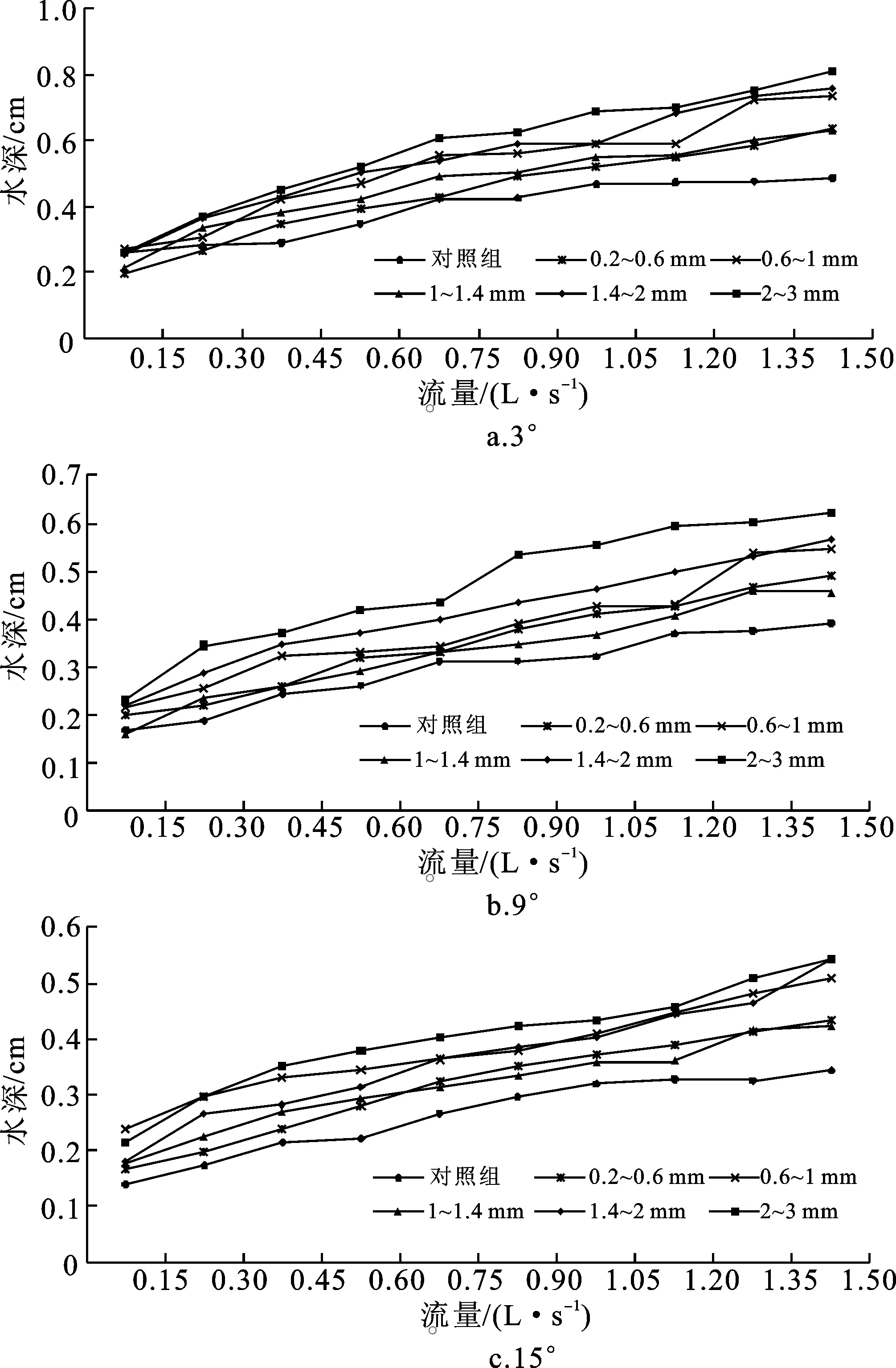
图4 不同坡度和粗糙度下坡面流水深Fig.4 Overland flow depths under different slopes and roughness

同样,对水深(h)与流量(Q)、坡度因子(S)和粗糙度因子(d)进行幂函数多元回归拟合,得到

h=0.289Q0.435S-0.236d0.083,R2=0.932。

流量Q和粗糙度d的幂指数为正值,说明水深随流量和粗糙度的增加而增加;坡度因子S的幂指数为负值,说明水深随坡度的增加而减小;决定系数较高,可见流量、坡度、粗糙度可以较好地表达坡面流水深。

2.3 坡面流流型、流态

水流流态一般用雷诺数Re来表示,不同床面粗糙度下Re变化见表2。由表2可知,本研究的定床下垫面条件下,坡面流大多属于层流和过渡流,雷诺数范围为230～3 399。

表2 不同坡度和粗糙度下坡面流雷诺数Tab.2 Reynolds number of overland flow under different slopes and roughness

相同粗糙度和坡度下,雷诺数随着流量的增大而增大,因为流量的增加会增大水流的惯性力,对水流黏滞力的克服更加明显,故而雷诺数逐渐增加,水流趋于紊动[8]。等坡度等流量条件下,雷诺数最大值均出现在无粗糙度布设的对照组下垫面,原因是粗糙度的布设增加了坡面流阻力,减小了水流的惯性力,降低了水流的紊动性,故而使雷诺数相应减小[10]。但不同粗糙度间雷诺数变化无明显规律,由公式(2)可知,水深和流速的乘积为单宽流量,黏滞系数由水温决定,本研究各试验场次水温几乎相同,故雷诺数在不同粗糙度间变化不明显。流态变化规律与前人得到的研究结果相近,但已有研究仅认为流态随粗糙度增加倾向层流流态,并未表现明显趋势[21]。

水流流型一般用弗劳德数Fr来表示,其反映水流的惯性力和重力之比。不同床面粗糙度下弗劳德数变化见图5。本研究的坡面流Fr范围为0.54～2.46。相同粗糙度和坡度下,弗劳德数随流量的增加基本呈增加趋势,流量的增大使坡面流更加趋于惯性力起主导作用;同坡度同流量下,弗劳德数与粗糙度呈负相关变化,随着粗糙度的增加,坡面流的流型由急流向缓流发展。

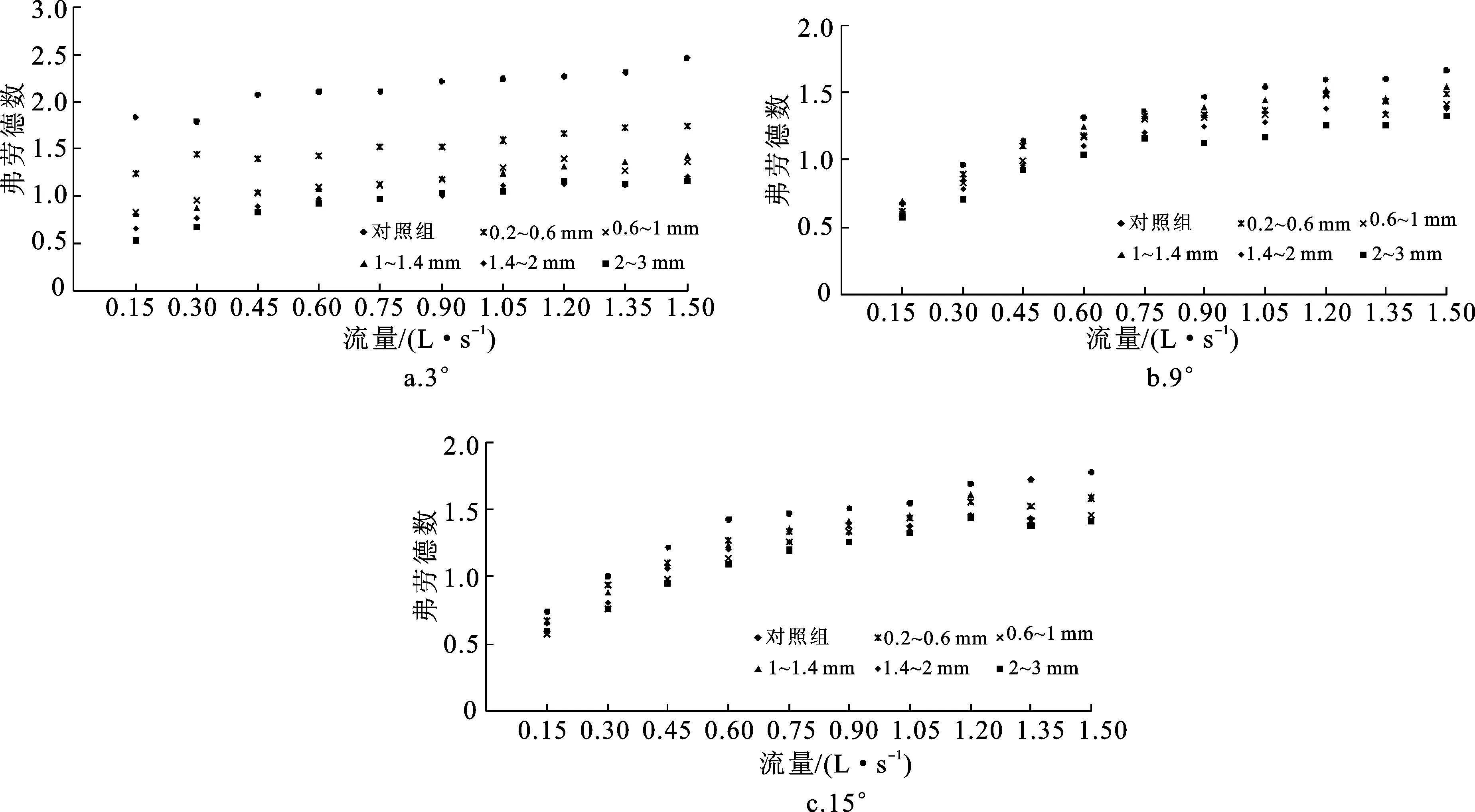
图5 不同坡度和粗糙度下坡面流弗劳德数Fig.5 Froude number of overland flow under different slopes and roughness

2.4 阻力系数

坡面流在流动过程中会受到阻力的影响,Darcy-Weisbach阻力系数f反映下垫面对水流的阻力大小。本研究在3°、9°和15°坡度下的阻力系数分别为0.07～1.44、0.08～2.62和0.07～2.57。

由图6可知,在相同坡度和粗糙度条件下,阻力系数随流量的增加呈减小趋势,且粗糙度越大,阻力系数的变化程度越明显。相同坡度和流量条件下,阻力系数随粗糙度的增加而增加,说明粗糙度的增加使水流克服阻力所消耗的能量增加。在坡面治理中,适当提高地表粗糙度,可以有效增加水流克服阻力的能量消耗,削弱水流对坡面土壤的侵蚀,进而有效控制水土流失。

图6 不同坡度和粗糙度下坡面流阻力系数Fig.6 Resistance coefficients of overland flow under different slopes and roughness

通过回归分析,得到阻力系数(f)与流量(Q)、坡度因子(S)和粗糙度(d)间的幂函数关系,回归方程为

f=0.481Q-0.688d0.710S0.288,R2=0.93。

回归方程决定系数较高,说明坡面流阻力系数可以被流量、粗糙度和坡度3个因子进行较好的表达。

为进一步研究不同流态下阻力系数的变化趋势,将坡面流阻力系数f与雷诺数Re进行拟合分析,不同粗糙度布设条件下阻力系数与雷诺数之间的回归关系见表3。阻力系数随雷诺数的增加呈幂函数递减,可见在水流流态趋于紊流的过程中,阻力系数不断减小。随着粗糙度的增加,拟合函数的幂指数绝对值逐渐增大,表明阻力系数随雷诺数的递减变化更为强烈,可见粗糙度的增加使坡面流对流态的敏感性提高。雷诺数Re的幂指数绝对值变化范围为0.34～0.733,与余冰等[10]和翟艳宾等[22]的研究结果相似。

2.5 径流剪应力

如前所述,本研究采用自制的设备直接测定径流剪应力,其具有更加简便、准确等优势。为了对其精准性进行验证,将光滑下垫面在3°、9°、15° 3个试验坡度和10组流量下的计算剪应力与实测剪应力进行比较(如图7)。结果显示,实测值与计算值相近,平均相对误差为17.49%。间接计算法作为一种普适性强且准确度较高的计算方法,其获得的试验结果较为可靠,但因其计算时需要用到流速、水深等试验过程中人为测定的数据,相对耗时长和更加复杂。本研究结果显示两者间数值相差较小,而直接测定方法具有快捷性及相对准确的优点,且试验装置的设置合理,因此为今后开展相近试验条件下径流剪切力的获取提供了一种简便而准确的方法。

图7 计算径流剪应力与实测径流剪应力关系Fig.7 Relationship between calculated runoff shear stress and measured runoff shear stress

基于实测径流剪应力F的结果,不同粗糙度下径流剪应力在3种坡度下随流量的变化见图8。可以看出,各粗糙度下垫面的径流剪应力大体随流量的增加而增加。对于各流量,3°和9°坡面的径流剪应力最大值在1.4～2 mm粗糙度下垫面出现最多,2～3 mm粗糙度下垫面次之;15°坡面的径流剪应力最大值均出现在2～3 mm粗糙度下垫面,可见粗糙度的增加对径流剪应力的增加有一定作用。

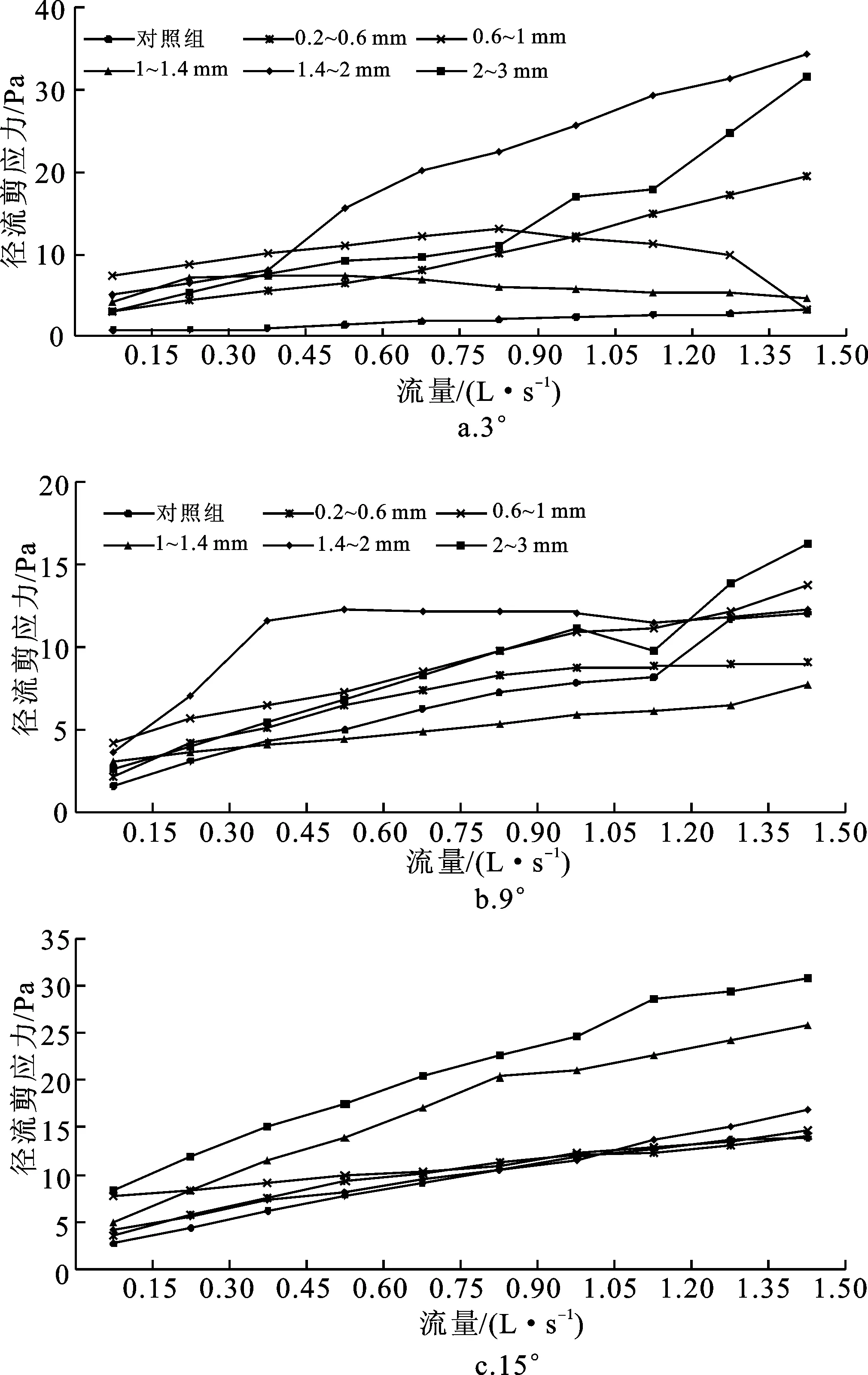
图8 不同坡度和粗糙度下径流剪应力Fig.8 Runoff shear stress under different slopes and roughness

对不同下垫面径流剪应力进行多重比较发现,6种下垫面的径流剪应力存在显著差异(P<0.05)。通过方差分析发现,粗糙度因子、流量因子和坡度因子对其均有显著影响(P<0.05)。对不同粗糙度下径流剪应力与坡度因子和流量因子进行拟合,得到表4,结果显示各粗糙度下径流剪应力均随流量的增大而增大;通过对各因子幂指数进行比较分析,认为相较坡度因子,流量因子对径流剪应力的影响更为明显。