多因素车位推荐融合算法研究

廖建聪，刘俐彤，秦军

（1.国网上海市电力公司崇明供电公司电力调度控制中心，上海 200000；2.中银金融科技有限公司工程管理部，上海 200000）

据查阅相关文献了解到，如今应用于车位推荐的算法只考虑路径。但车位的属性不仅只有距离，单从距离考虑过于简单。应当充分获取更多信息为车主进行停车位推荐。对于车位推荐分为选定影响的因素以及权重的分配。可以将影响车位的因素作为车位的固有属性，从而获取车位的属性值，另外通过信息与信息之间的联系并综合用户的偏好做出权重的分配。

1 车位推荐影响因素分析

影响因素中属于车位属性的有占用、温度、车位类型、车位周围状况。其次属于用户的属性的有车主住址、车主对于车位属性的重视情况。在此温度不仅仅是采集实时显示且需要建模完成温度预测提供可靠的推荐。车位类型有非字型、一字型、斜型。车位周围状况反映的是停车难度，分别为一边有车、两边有车、两边无车。用户属性中考虑的是车位距离以及车主对车位属性偏好重要程度的选择。

2 获取影响因素数据

车位状态根据超声波传感器获取，车位周围状况可通过车位状态反映，车位类型是固定值，温度数据通过温度传感器获取并进行实时预测，车位距离通过最短路径算法计算。

对于温度预测，选择在中短期预测适用性好且不需要大量数据支撑的ARMA 模型[1-3]。对于车位距离计算采用Floyd 算法。

2.1 温度预测

ARMA 模型表示为时间序列Xt，如式（1）所示。

式中：C 为常数，φ1…φp称为自回归系数，θ1…θq称为移动平均系数。ut-q是相互独立的白噪声序列。Xt-p为前期值。

通过ARMA 模型进行温度预测需要通过平稳性检测、模型识别、参数估计、残差检验后进行预测。

平稳性检测是通过ADF检验作为标准[4]。

模型识别的内容通过AIC（赤池信息准则）和BIC（贝叶斯信息准则）完成定阶，可能AIC 和BIC 得出的阶数不同，最后以计算量和样本容量的具体情况综合考虑。

设时间序列样本为{Xt|1≤t≤N}，AIC准则为式（2）定义为满足AIC为最小值的p、q即为满足AIC准则的阶数。BIC准则为式（3）定义为满足BIC 为最小值的p、q 即为通过BIC 准则阶数。

残差检验采用Durbin-Waston 统计量进行，对于{ut}建立的统计量如式（4），DW统计量越接近2 表示越不存在相关性。

式中：ut为模型中白噪声序列。

2.2 车位距离计算

Floyd 算法[5]，用于多源最短路求解，类型为动态规划类，步骤如下。

（1）初始n×n 阶阵，矩阵元素分别表示点与点之间距离，若不存在一次到达的点，则元素值为无穷，若存在则为对应定点间初始距离，对角线为0。

（2）逐步在原路径中加入试探顶点，若加入后导致路过这点后原路径变短则更新初始距离值，否则不对其发生变化，直到所有试探顶点加入完毕。

3 处理影响因素数据

为了进一步对车位属性进行分析，我们通过集合A={aj|j=1,2,3,···,n}表示。a1为车位温度，成本型属性；a2为车位距离，成本型属性；a3为车位类型，效益型属性；a4为周围车况，效益型属性。

对于属性说明：成本型属性，代表越小越好；效益型属性与成本型相反，越大越好。首先按照属性值构建决策矩阵Xm×n=(xij)，后按照属性不同规范化为矩阵Sm×n。

4 分配影响因素权重

因素权重采用组合赋权法分配，主观权重采用层次分析法，客观权重采用熵值法[6]。设车主对于属性aj的主观权重为Swj，客观权重为Owj。

则属于属性aj的权重Wj计算如式（5）。

式中：a、b 为权重分配系数，Swj为主观权重，Owj为客观权重。

对于分配系数与主客观权重应满足式（6）、（7）。

式中：a、b 为权重分配系数，Swj为主观权重，Owj为客观权重。

4.1 主观权重Swj 计算

主观权重的计算方法选择为层次分析法[7]。

利用层次分析法计算主观权重步骤：判断矩阵构造、一致性检验。

4.1.1 构造判断矩阵

根据车主对于车位属性的重要性程度进行确定，仅凭车主对每个属性打分客观性差，所以引入1-9 标度方法进行对判断矩阵构造。设判断矩阵为On×n(oij),i≤n,j≤n。

判断矩阵元素oij构造方法为式（8）。

式中：c表示属性ai对于属性aj的重要性程度，c根据表1 进行选择标度。

表1 1-9 标度法

4.1.2 一致性检验

获取判断矩阵后，由OSw=λSw 求出O对应最大特征值λ对应的特征向量Sw。其次需对其做一次性检验以此求证判断矩阵的有效鉴别性。一致性检验中先对一致性指标CI计算，再根据一致性指标CI与RI值对一致性比率计算。

4.2 客观权重Owj 计算

客观权重采用熵值法。通过熵值法计算客观权重的计算步骤为决策矩阵归一化、计算熵值、计算差异系数、计算aj客观权重。

将之前规范化后的决策矩阵Sm×n按照式（9）进行归一化处理为矩阵Pm×n。

式中：Pij为归一化后的决策矩阵，Sij为规范化决策矩阵。

属性aj熵值ej计算如式（10）。

差异系数gj计算如式（11）。

属性aj客观权重Owj计算如式（12）。

5 灰色关联决策矩阵

为了减少权重在计算过程中的偏差，需在决策矩阵上计算灰色关联[8]。

假设最佳停车位为B0={s0j|j=1,2,···,n}，用δij表示最佳停车位B0与空余停车位Bi相对于属性aj的规范化决策值soj,sij之间的灰色关联系数计算如式（13）。

式中：ρ∊[0,1]为分辨系数，本算法中取0.5，Sij为规范化矩阵元素。

利用灰色关联系数构造灰色关联系数矩阵Rm×n，如（14）所示。

通过对灰色关联系数矩阵Rm×n进行加权得灰色关联决策矩阵Fm×n，如（15）所示。

6 匹配车主最佳车位

当灰色关联决策矩阵F 获取之后便可以进行对最佳停车位计算。计算方法有标准信息法、字典法、理想解法（TOPSIS）[9]。本推荐算法中选取TOPSIS 作为最佳停车位计算方法。

首先通过选取灰色关联决策矩阵中每列最优的数据和每列最差的数据作为理想解V+和负理想解V-，表达如（16）、（17）所示。

计算灰色关联决策矩阵各个车位与正负理想解之间的距离，如式（18）、（19）所示。

相似度计算如式（20）所示。

相似度越靠近1 越表示与理想值越接近，通过选取Li中最接近1 的车位作为匹配车主的最佳停车位推荐。

7 应用实例

我们以上海某小区内部停车区域作为应用分析，其中关于车位对应每个楼栋的距离是提前通过Floyd 算法计算，车位类型是提前写入至车位对应数据表存储至服务器中数据库中的数据表内，关于温度、温度预测、周围车况是动态计算并更新至对应车位的数据表内。假设当前车主居住楼栋为9 号楼，此时空余车位编号为65、194、212、172，即m=4，n=4。车主与车位相对应的属性值如表2 所示。

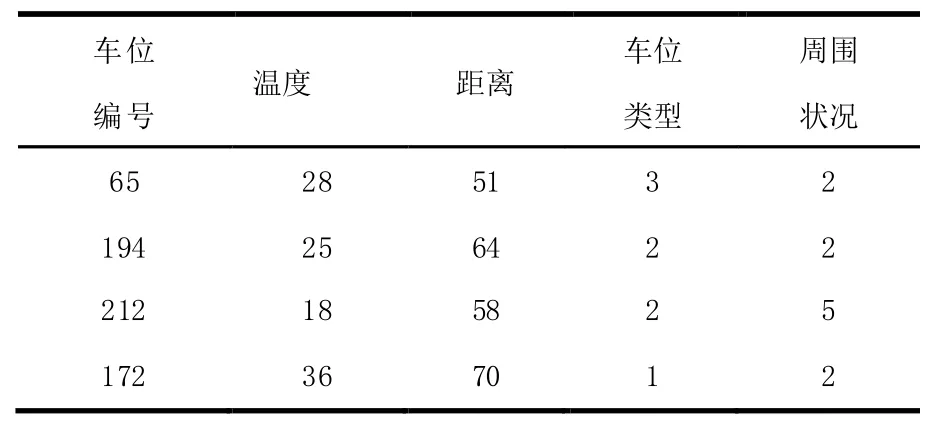
表2 车位对应车主属性值

根据属性值可以建立初始决策矩阵X4×4如（21）所示。

由于各个车主在进行选择属性倚重时都会不同，假设该车主根据1-9 标度法对于各个属性重要性判断矩阵O4×4如（22）所示。

根据判断矩阵O4×4所得其最大特征值以及最大特征值所对归一化特征向量如（23）所示。

其中归一化的特征向量Sw 为车主主观权重。

由判断矩阵计算一致性指标如（24）所示。

由于C.R≤0.1，故通过一致性检验。将决策矩阵X4×4进行规范化得矩阵S4×4如（25）所示。

对规范化决策矩阵S4×4进行归一化得矩阵P4×4如（26）所示。

由矩阵P4×4用熵值法求得属性熵值e=(0.9772,0.9950,0.9528,0.9293)，由e 可得g=(0.0228,0.0050,0.0472,0.0707)，由g 可知客观权重Ow=(0.1563,0.0346,0.3237,0.4853)。根据主客观权重距离可得分配系数a=0.8853，b=0.1147。

由主观、客观权重与分配系数相乘得最后的组合权重如（27）所示。

假设最佳车位B0的属性值为B0=(1,1,1,1)。由规范化决策矩阵S4×4计算可得灰色关联系数矩阵R4×4如（28）所示。

通过对灰色关联系数矩阵进行加权后如（29）所示。

从F4×4可得理想解V+与负理想解V-如（30）所示。

通过计算空余车位与理想车位之间的距离以及空余车位与负理想车位之间的距离如（31）所示。

根据D+,D-计算可得相似度L 如（32）所示。

如果按照传统只考虑距离进行推荐车位，则推荐车位为65 号车位，采用多因素车位推荐融合算法研究则进行推荐的车位编号是212 号。

8 结束语

本文创新性地拓展了车位推荐时的决策因素，在车位推荐时更高程度地体现了车主对于车位选择不同因素的重视程度。而且本算法以上海某小区内部停车区域为实验对象验证了可行性和准确性。该算法还可根据因素的要求增减，适应性强。能够为推进城市数字化转型，打造智慧小区，为智慧停车场助力。