基于相变材料Ge2Sb2Se4Te1的可切换边缘检测与聚焦成像超表面
2023-11-13唐紫依邓钦荣张汶婷黄奕嘉
胡 杰,唐紫依,蓝 翔,邓钦荣,张汶婷,黄奕嘉,李 玲
四川师范大学物理与电子工程学院,微纳光学实验室,四川 成都 610101
1 引言
图像处理在许多技术领域有着不可替代的作用。起初,图像处理的方法主要是通过集成电路在数字领域进行数学运算,但该方法运算速度慢、功耗高,限制了其进一步的应用[1-2]。为了解决这些问题,Solli等[3]在2015 年提出了基于光学器件的光模拟计算方法。这种方法通过操纵携带图像信息的光信号来进行图像处理。虽然通过光学模拟计算,图像处理可以更快更有效,但通常需要庞大的光学仪器配制[4],这不适用于高集成度的现代光学系统。最近,一种二维亚波长结构-超表面,凭借对电磁波的偏振、振幅和相位的控制能力[5-16]引起了广泛的关注。在过去的几年里,许多基于超表面的新方法被提出用于各种光学元件和系统,包括全息图[17-21]、光束整形[22-23],次级衍射成像[24-25]、电磁隐身[26-27]等等。与此同时,超表面也作为边缘检测中的空间微分器被用于光学模拟计算类的图像处理[28-30]。近年来,有一些研究利用精细设计的超表面结构实现了二维边缘检测[31-34]。Huo 等[33]基于超表面与4f 成像系统的结合,通过切换入射光的偏振态实现了边缘检测与明场成像之间的动态切换,提取了物体上的不同形态信息,扩展了超表面的应用场景;He 等[34]演示了无需4f 成像系统的二维边缘检测,进一步提高了超表面的集成度。
尽管相关研究已经取得相当大的进展,但上述超表面在本质上仍然是静态的,其光学性质在制造完成时就已固定,不利于超表面的进一步应用。因此,越来越多的研究聚焦于主动调控超表面。在此过程中,相变材料是超表面动态控制中非常重要的一部分。迄今为止,已有多种不同的调制方法被运用研究各种功能材料,如导电氧化物、石墨烯、液晶和相变材料(PCMs)[35]。其中,Ge2Sb2Te5(GST)是一种典型的相变材料,由于其在外界刺激下由晶态转变为非晶态时折射率差异较大而得到了广泛的应用[36-37]。并且,GST的晶态和非晶态在室温下稳定,具有高折射率差异和更快的开关速度[38-42]。但晶态GST 在红外光范围内的光学损耗限制了它的应用。近年,通过将GST 中的Te 原子替换为Se 原子,出现了一种新的相变材料Ge2Sb2Se4Te1(GSST)。与GST 相比,GSST 不仅具有上述优点,并且在红外光谱范围内的光学损耗极低[43]。
基于上述背景,本文提出了一种基于GSST 的单片超表面,在不需要4f 成像系统辅助的情况下,可实现边缘检测与聚焦成像之间的动态切换。超表面被设计在两种结晶状态下实现两种不同的图像处理机制。通过不同结晶态下的传输相位和几何相位组合,左旋圆偏振光束和右旋圆偏振光束(下文简称LCP 光和RCP 光)将携带不同的相位。通过优化这些相位,可以分别实现边缘检测和聚焦成像两种功能。图1 为超表面在边缘检测和聚焦成像之间动态切换的示意图。动态开关功能依赖于GSST 的可变结晶状态。当GSST 为晶态(crystalline)时,出射光会在像面直接显示太阳神鸟边缘。当GSST 为非晶态(amorphous)时,出射光可以直接成像太阳神鸟。为了方便后文分别简称晶态GSST 和非晶态GSST 为c-GSST 和a-GSST。
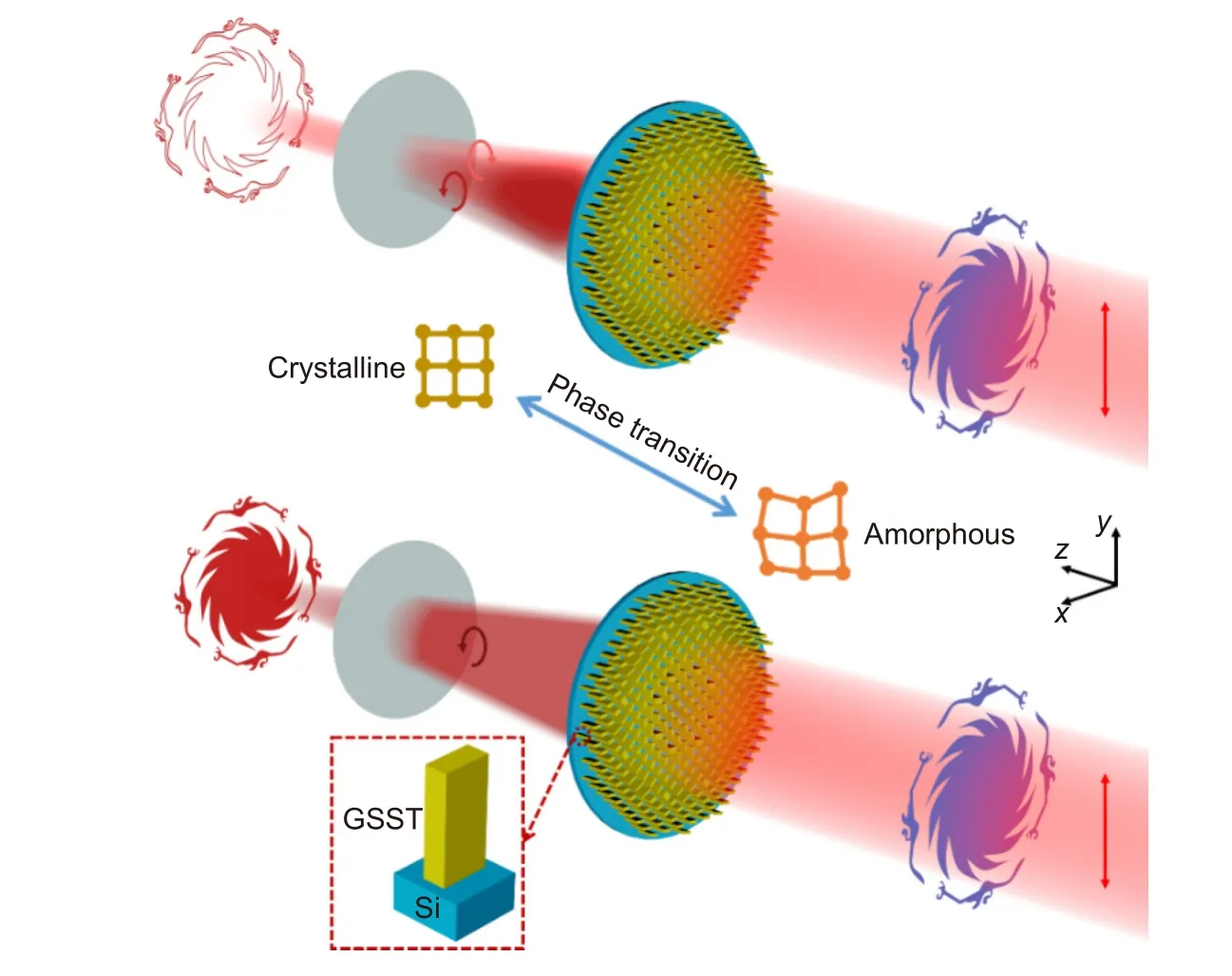
图1 基于GSST 相变实现边缘检测和聚焦成像间动态切换的超表面原理图Fig.1 Schematic of the metasurface platform enables dynamic switching between the edge detection and imaging based on the phase transition of GSST
2 单元结构设计与梯度超表面仿真
图2(a)和2(b)中的GSST 柱可视为弱耦合的低质量因子法布里-珀罗谐振腔,传输相位和交叉偏振系数几乎不随旋转角θ的变化而变化[44]。这种情况下,几何相位起源于光子自旋轨道相互作用(the photonic spin-orbit interactions,SOIs),它只与GSST 柱的旋转角度有关[45],而传输相位只与单元结构的固有性质有关,包括材料、形状和大小。这使得几何相位和传输相位可以自由组合,因此不同GSST 结晶态下的不同旋向圆偏振光(LCP 和RCP 光)将会得到不同的总相位。以单个各向异性光散射体为例进行分析,假设一个透明的各向异性散射体可以引入传输相位φ,当该散射体旋转角度为θ(相对x轴逆时针旋转),总相位写作2σθ+φ(σ=±1,对 于LCP 和RCP 光,σ分别等于+1 和-1)。通过观察不同状态下的相位表达式,当使用具有相同固有特性但旋转角度变化的单元结构时,由于传输相位φ是不变的,相对相位分布只依赖于几何相位,透过超表面的LCP 光和RCP 光将具有相反相位分布,即对称SOIs[46]。利用各种尺寸和旋转角度同时变化的单元结构时,通过传输相位和几何相位的共同贡献,LCP 光和RCP 光可以具有任意的相位组合,即非对称SOIs[46]。传统不可调谐材料的超表面具有固定的SOIs 类型,该特性限制了超表面功能的进一步开发。而由于c-GSST 和a-GSST 具有不同的介电常数,超表面在不同的GSST 结晶态下也会对应有φc和φa两个传输相位,由此当φc和φa分别具有上述两种传输相位特点时,即可得到可调控SOIs。
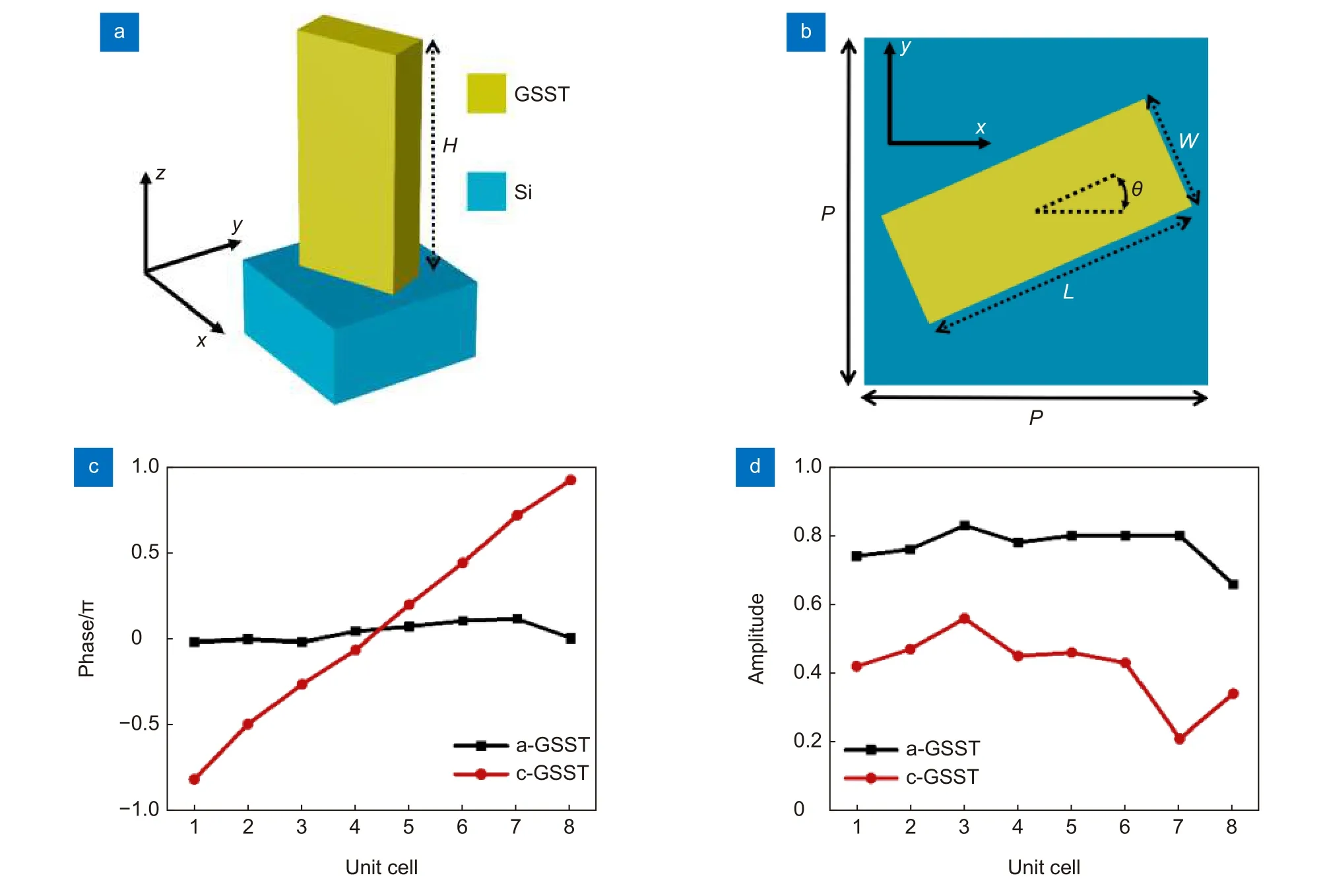
图2 (a,b) 不同视图下的单元结构示意图;(c,d) 10.6 μm 波长下八个单元结构的相位响应和交叉偏振系数。方柱结构和基底的材料分别是GSST 和Si。恒定参数(高度、周期):H=6 μm,P=4 μm;八个单元结构的长度(L)和宽度(W)分别为L=2.9 μm,3.0 μm,3.3 μm,3.2 μm,3.5 μm,3.79 μm,3.82 μm 和2.68 μm,W=1.34 μm,1.28 μm,1.2 μm,1.14 μm,1.0 μm,0.83 μm,0.8 μm 和1.41 μmFig.2 (a,b) Schematic illustrations of unit cells at different views.(c,d) Simulated phase responses and cross-polarized coefficients of eight unit cells for circularly polarized light at the wavelength of 10.6 μm.The materials of nanofins and substrate are GSST and Si,respectively.Constant parameters: H=6 μm,P=4 μm.The length (L) and width (W) of eight unit cells are L=2.9,3.0,3.3,3.2,3.5,3.79,3.82 and 2.68 μm,W=1.34,1.28,1.2,1.14,1.0,0.83,0.8 and 1.41 μm
基于上述结论,本文优化设计了一组实现可调控SOIs 的单元结构。不同单元结构的电磁响应在CST 微波工作室频域求解器中使用有限积分技术进行了模拟计算,其中边界条件x和y方向设置为unit cell,z方向设置为open;入射波波长为10 μm~11 μm。图2(a)和2(b)中显示了相关几何参数(L,W,P,H)。当工作波长为10.6 μm 时,c-GSST 和a-GSST 的折射率n分别为4.16 和3.18[43],底层材料硅(Si)的折射率n=3.42。从图2(c)和2(d)中可以看出,通过调整纵横比(L/W),c-GSST 下单元结构的传输相位能覆盖整个0~2π 范围,a-GSST 下单元结构的传输相位几乎一致,从而实现了可调控SOIs。单元结构的平均交叉偏振透射系数达到 0.77(a-GSST)和0.42(c-GSST),与相关研究处于同一水平,能够在红外光谱范围内正常工作[47]。
为了证明该设计的通用性和有效性,在CST 微波工作室时域求解器中使用有限积分技术(FIT)模拟计算了透射光在GSST 不同结晶态下的异常折射。其中边界条件x和y方向设置为periodic,z方向设置为open;并设置了足够的网格单元用以捕捉场分布,减少误差。入射光源采用波长为10.6 μm 的圆偏振光。图3(a)为设计的长度为32 μm 的梯度超表面示意图。非晶态和晶态下梯度超表面的传输相位梯度分别为0和π/4。每个相邻单元之间的旋转角度之差(Δθ)为π/8。梯度超表面理论设计用于在a-GSST 下表现对称SOIs,得到RCP 和LCP 出射光的对称折射角分别为-17.1°和17.1°。在c-GSST 下表现非对称SOIs,RCP 和LCP 出射光的折射角分别为0°和32°。对应的模拟结果如图3(b)和3(c)所示:在a-GSST 下,模拟折射光偏转角度为-19.5°和17.7°;在c-GSST 下,折射光偏转角度角分别为0°和31.2°。通过对仿真结果与设计角度的比较,可以发现两者一致性较好,其中存在的细微误差经分析源于单元结构间的振幅和相位匹配不完美。
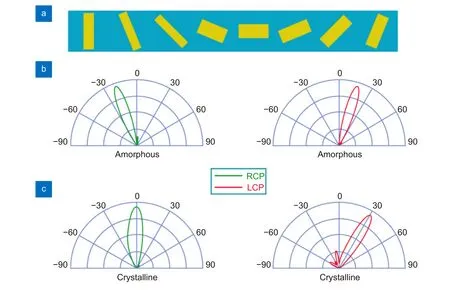
图3 (a) 可调谐异常透射梯度超表面周期结构示意图;(b) a-GSST 下的模拟交叉偏振远场分布;(c) c-GSST 下的模拟交叉偏振远场分布Fig.3 (a) Schematic illustration of a periodic gradient metasurface for tunable anomalous transmission;(b) The simulated cross-polarized far-field distributions when GSST is amorphous;(c) The simulated cross-polarized far-field distributions when GSST is crystalline
3 成像功能分析设计与验证
为了实现可切换边缘检测与聚焦成像单片超表面,下面对两者原理进行简单分析。首先,对于聚焦成像,相位分布ψ与坐标x和y之间的关系为
其中:λ是入射光波长;f是焦距。
与聚焦成像相比,边缘检测的机理更为复杂。为了方便起见,先对一维边缘成像的工作原理进行分析。在携带物体信息的线偏振光的照射下,具有几何相位梯度分布的超表面投射出具有对称折射的LCP 和RCP 光,导致LCP 和RCP 图像分别发生横向偏移±l。因此电场可表示为
当l远小于成像尺寸时,LCP 光和RCP 光在同一点上的相位可视为是相等的。因此,LCP 和RCP图像的重叠区域将会保持入射时的偏振态,用正交线性偏振器进行滤波,最终的电场可以改写为
由于与整个成像相比,l可以忽略。因此,Eedge(x,y) 与入射电场E0(x,y)的一阶空间微分近似成正比:
因此,边缘检测的关键过程就简单地分为成像、分离和过滤三个步骤[48]。为了同时实现成像和分离,两相分布应表示为
其中:λ是入射波长;f是焦距;σ=±1(对于LCP 和RCP 光,σ分别等于+1 和-1);n是一个控制LCP 和RCP 图像分离程度的变量实数,n的大小与分离程度成反比。因此,边缘宽度取决于选定的n值和所设计超表面的衍射极限。对于二维边缘检测,分离过程拓展为LCP 和RCP 图像沿着径向等比例缩小和放大,利用正交线性偏振器进行滤波。因此,同时进行成像、分离是实现边缘检测的重点。通过分析和优化,单元结构在c-GSST 的传输相位和偏转角分布设计如下:
其中:φc(x,y)是晶态下的(x,y)坐标处相位,θ(x,y)为对应坐标处单元结构旋转角度,rmax是圆形超表面的半径,f1和f2分别是边缘检测和聚焦成像的焦距。采用这种设计方法,在a-GSST 下,超表面对LCP和RCP 透射光赋予的总相位由相同的传输相位和相反的几何相位组成,因此 LCP 光会获得聚焦相位,RCP 光会获得相反的发散相位,因而利用LCP 光可实现焦距为f2聚焦成像。在c-GSST 下,超表面的传输相位为聚焦相位,几何相位会分别在该聚焦相位的基础上叠加一个聚焦相位和发散相位,当f2满足式(8)时,该叠加相位可以将LCP 和RCP 图像沿着径向等比例缩小和放大,从而实现焦距为f1的边缘检测。
最后,为验证式(6)和式(7)分布设计的可行性,建立了相应的超表面模型。超表面由30×30 个单元结构组成,尺寸为120 μm ×120 μm,相关参数分别为λ=10.6 μm,rmax=60 μm,f1=100 μm,f2=1000 μm;c-GSST 和a-GSST 的折射率n分别为4.16 和3.18,底层材料硅(Si)的折射率n=3.42;GSST 方柱高度H=6 μm。在CST 微波工作室时域求解器中使用有限积分技术进行了模拟仿真。模拟仿真目标分布应为圆环形(焦点边缘)和圆点形(聚焦焦点)分布,模拟仿真结果如图4 所示。从图4(a)和4(b)可以看出c-GSST下RCP 和LCP 图像以及中心虚线部分归一化强度分布沿径向实现了一定程度的分离,与设计一致。图4(c)和4(d)分别显示了经偏振滤波之后的像面强度分布和聚焦的中心强度分布,其中图4(c)为LCP和RCP 两部分叠加后,经正交偏振滤波之后的像面强度分布。同时各强度分布均存在大小不同的背景噪声。图4(a)、4(b)和4(d)中存在的杂散光与仿真模型大小、网格划分大小以及各单元交叉偏振系数分布不均有关。模拟仿真结果中较强的杂散光主要体现在图4(c)中,由于过滤后中心部位强度降低,周围的噪声相对强度有所上升,通过对比图4(c)与图4(a)和图4(b)中的背景噪声可以加以验证。图4(c)和4(d)中的圆环形边缘能量效率和圆点形焦点能量效率分别为25.4%和31.6%,这里的能量效率为相对能量效率是像面上有效部分能量与像面总能量之比。通过观察不难发现图4(c)和4(d)中经偏振滤波之后的像面强度分布和中心强度分布分别为圆环形和圆点形,其中心虚线部分归一化强度分布也呈现出对称双峰和聚焦单峰的形态验证了该设计的可行性。但同时也发现像面强度分布图像存在强度分布不均匀从而导致的边缘检测效果欠佳的问题,经分析该问题主要源于计算能力限制下仿真模型较小和网格设置不足,通过增加仿真模型体积和进一步细化网格还可以进一步提高边缘检测效果。为了验证上述分析,在Matlab 中进行了理论模拟计算以验证式(6)和式(7)相位分布下实现边缘检测与聚焦成像的可行性,设定参数为:λ=10.6 μm,rmax=600 μm,f1=600 μm,f2=15000 μm。图5(a)和5(b)分别显示了以“S I C N U”字母和太阳神鸟为成像物体时在焦平面的成像效果。从图中可以看出聚焦成像与边缘检测效果良好,验证了上述分析,并证明了该相位设计的可行性。最后,图5(c)是用于边缘检测的成像系统示意图。与其他同类图像处理系统相比,该设计摆脱了4f 成像系统,进一步实现了小型化和高集成化。

图4 入射光为10.6 μm 时GSST 不同态下像面强度分布。(a) c-GSST 下,z=100 μm 时模拟RCP 成像强度分布和中心虚线部分归一化强度分布;(b) c-GSST 下,z=100 μm 时模拟LCP 成像强度分布和中心虚线部分归一化强度分布;(c) c-GSST 下,z=100 μm 时模拟偏振滤波后的像面强度分布和中心虚线部分归一化强度分布;(d) a-GSST 下,z=1000 μm 时模拟聚焦成像强度分布和中心虚线部分归一化强度分布Fig.4 The simulated image intensity distributions of different states under the 10.6 μm incident beam.(a) The simulated RCP image intensity distributions and normalized intensity distributions of the dotted line on z=100 μm plane when GSST is crystalline;(b) The simulated LCP image intensity distributions and normalized intensity distributions of the dotted line on z=100 μm plane when GSST is crystalline;(c) The simulated edge image intensity distribution and normalized intensity distributions of the dotted line on z=100 μm plane when GSST is crystalline;(d) The simulated LCP image intensity distribution and normalized intensity distributions of the dotted line on z=1000 μm plane when GSST is amorphousSST is amorphous
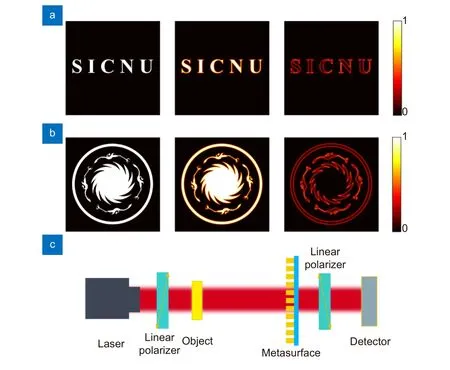
图5 (a) 理论模拟计算成像物体为“S I C N U”字母时,从左到右依次为:物体图像,聚焦成像,边缘检测成像;(b) 理论模拟计算成像物体为太阳神鸟时,从左到右依次为:物体图像,聚焦成像,边缘检测成像;(c) 图像处理系统示意图Fig.5 (a) The calculation results when the object is "S I C N U",from left to right: object image,imaging,edge detection imaging;(b) The calculation results when the object is the sun and immortal birds,from left to right: object image,imaging,and edge detection imaging;(c) Schematic illustration of the system for image processing
4 结论
综上所述,本文提出了一种可切换聚焦成像与边缘检测的单片超表面,超表面由基于GSST 相变材料的单元结构组成。基于GSST 的单元结构通过GSST的结晶态转换实现了可切换光子SOIs。并通过利用可切换光子SOIs 的特性设计了可切换边缘检测与聚焦成像超表面。最后通过模拟仿真和理论计算验证了该设计的可行性。本文提出的超表面无需4f 成像系统的辅助,进一步提高了超表面应用的集成度,为有源元器件的设计提供了新的思路,在生物医学成像和缺陷检测等领域有潜在应用价值。
