超表面实现复杂矢量涡旋光束的研究进展

柯 岚，章思梦，李晨霞，洪 治，井绪峰*

1 中国计量大学光学与电子科技学院，浙江 杭州 310018；

2 中国计量大学太赫兹技术研究所，浙江 杭州 310018

1 引言

超表面(Metasurface)是由微纳结构排列而成的二维器件[1]，是超材料的平面化[2-4]，可以通过精确的调控结构来控制光的传播和相位[5-7]。相比于传统的三维结构，超表面具有体积更小、制备更容易、控制更精准的优势[8-11]。它通常为亚波长结构，可以广泛应用于光电子学、量子光学、光子学等领域[12-13]。超表面不仅能够实现高效的折射、反射和透射，还可以实现精确的相位调控、拓宽波束角度等功能[14-17]。此外，超表面还可以有效地抑制杂散光的干扰，实现更高质量的光学成像和传输[18-21]。最近，超表面已经被广泛应用于多种光学器件的设计制备，如透镜[22]、偏振器[23]、色散器[24]、光学互联器[25]、光学传感器[26]等，推动了光学技术的快速发展[27]。

超表面实现电磁波波前调控的主要原理大致可以分为传输相位型、几何相位型和共振相位型[28-30]，这里主要介绍传输相位型与几何相位型超表面。传输相位型超表面主要利用电磁波在传播过程中累积的相位差来实现相位调控的，传统的传输相位光学器件大多采用曲面结构，使器件厚度随空间变化对电磁波进行调制[31]。二元光学器件虽然将器件厚度离散化，但仍然至少存在两种厚度，这两种方式都会使得器件外形非平面，不利于集成和共形设计[32]。超表面可以通过调节每个单元的尺寸，而非厚度，来改变赋予入射光束的传输相位。这使得超表面能够在保证功能实现的同时保持平面特性。同时，传输相位的累积与材料折射率息息相关，提高等效折射率可以有效减少超表面的厚度[33]。几何相位型超表面利用电磁波在偏振态转化过程中不同的几何路径差，超表面设计中的几何相位大多以Pancharatnam-Berry (PB)相位原理为基础[12]，即使用圆偏振光垂直入射时，旋转单元结构角度为ɑ(逆时针旋转)，当其经过各向异性的介质就会产生偏振变化，其交叉极化部分会携带一个exp (2iɑ)的额外相位因子。所以，几何相位由于其存在共同的发现者，也被称为Pancharatnam-Berry (PB)相位。根据这个原理，当一束光发生偏振变换时，会产生一个额外的相位差，该相位差就是所谓的PB 相位。这个额外的相位差是由于不同偏振状态下不同的相位差异造成的，并且与光程差无关。

对传输相位和几何相位理论的运用可以对入射电磁波的相位进行精确且灵活的调制，为波前赋予灵活的相位分布，这就确保了我们可以将超表面与矢量光束的生成结合起来[34-38]。矢量光场是指同一时间在同一波振动面上的不同位置具有不同偏振态的光场，在空间分布上具有非均匀偏振态分布。与标量光场不同，其光束横截面上的偏振态会随空间位置变化而变化[39-41]。除了在局部区域内包含线偏振，矢量光场还可以包含圆偏振和椭圆偏振，基本光束的偏振度变化使得矢量光场的描述更加复杂[42-44]。除偏振特性外，螺旋相位的引入会为矢量光束带来更多复杂且有趣的特性，对于具有不同偏振态与相位分布的矢量光束，研究者们一般选择改良庞加莱球来对其进行表征[45-46]。传统光学生成矢量光束的方式光路较为复杂，并且需要较多的光学元件。将矢量光场与超表面进行结合，利用超表面小型化、易于集成的优点方便灵活地生成具有不同特性的矢量光束，基于传输相位、几何相位以及二者的结合，在不同频段，不同功能上选择合适的材料进行构建[15]。由于矢量光场拥有复杂且大量的类型，无法以此来分类，因此本文主要从材料角度出发，探讨介质型超表面、金属型超表面以及智能超表面在生成不同矢量光场模式上的发展，全介质超表面的构成材料全部都是电介质材料，金属超表面可以是纯金属，或是金属与介质的组合，智能超表面则是在金属与介质超表面的基础上集成可调的电子元器件或者介电材料[36,47]，这三种超表面设计思路接近且各有优势，可以根据设计需求选择。

2 全介质超表面生成涡旋光束

全介质超表面是指使用介质材料构成的超表面结构，常常使用压电材料、各向异性材料等构成[48-49]。金属型超表面在高频段会存在较大的吸收损耗，而介质型超表面可以通过选择低损耗的材料来降低能量损耗，提高能量利用率[50-52]。同样地，介质超表面可以在不涉及厚度调节的情况下，通过调节亚波长结构的几何尺寸与旋转来实现对光束的调控，例如可用于实现偏振转换、波的操控、光的分离与聚焦、光子集成等功能，广泛应用于光通信、光电子学、光学成像、传感器等领域[38,53-55]。

首先是利用全介质超表面进行标量涡旋光束生成的研究，涡旋光束具有的特殊性质可以在光学与量子光学等领域发挥重要作用。涡旋光束的相位呈现螺旋形分布特征，与自然界中的漩涡类似，涡旋相位在中心处的相位奇点由于自身的干涉相消特性，光强趋于零点，因此在场强分布上表现为中心强度为零的空心环状分布。涡旋光束中的每个光子都会携带有轨道角动量(orbit angular momentum,OAM)，其值为，其中l为拓扑荷数，是一种量子数，用于描述光束中涡旋的数量和方向，理论上可以是任意值；则是约化普朗克常量。涡旋光束具有的每种拓扑荷l都对应一种独立的模场状态，且每种状态各自正交，互不干扰，因此涡旋光束可以广泛应用于微粒操控、显微成像、光学测量、量子信息处理、光通信等领域[2,56-59]。

由于涡旋光束已经被广泛应用，目前人们的注意力更为集中在如何高效地制造它们。之前利用超表面生成OAM 光束的探究受限于使用几何相位和拓扑光子学时的基本对称性限制，无法自由的控制生成涡旋光束的手性、自选角动量和轨道角动量[60-62]。早在2017 年Li 等人就创造性地总结了超表面的不同调控方式，包括不同OAM 光束的产生，以及Zhang 等人提出的利用全介质超表面生成OAM 光束[63-64]。2020年Hend Sroor 等人提出了一种全介质超表面[65]，能够打破自旋和轨道状态的对称性，利用超表面的特性将具有复杂拓扑荷OAM 光束的生成功能进行片上集成，如图1(a)所示，从激光源实现任意角动量控制。在这里，这篇文章提出的全介质超表面克服了这一限制，在前人的基础上提出了新的设计方案。这种超表面能够产生任意所需的手性光状态，包含非对称拓扑荷的OAM 值，更加自由地实现超手性光的生成。激光器腔内由非线性晶体(KTP)、偏振转换器(Pol)、超表面(J-plate)以及耦合器(OC)构成，并由红外泵浦源激发。该论文涉及超表面的工作波长为532 nm。构成超表面的单元结构是正方形熔融石英衬底上的非晶TiO2纳米柱，如图1(b)所示。将入射光束分解为一对正交线偏振分量(水平和垂直分量)的叠加，纳米柱的高度为600 nm，通过调节柱的长轴Wx和短轴Wy的大小，为入射光束的正交极化分量分别施加不同的相位延迟δx和δy，从而调控整体出射光束的偏振与相位特性。

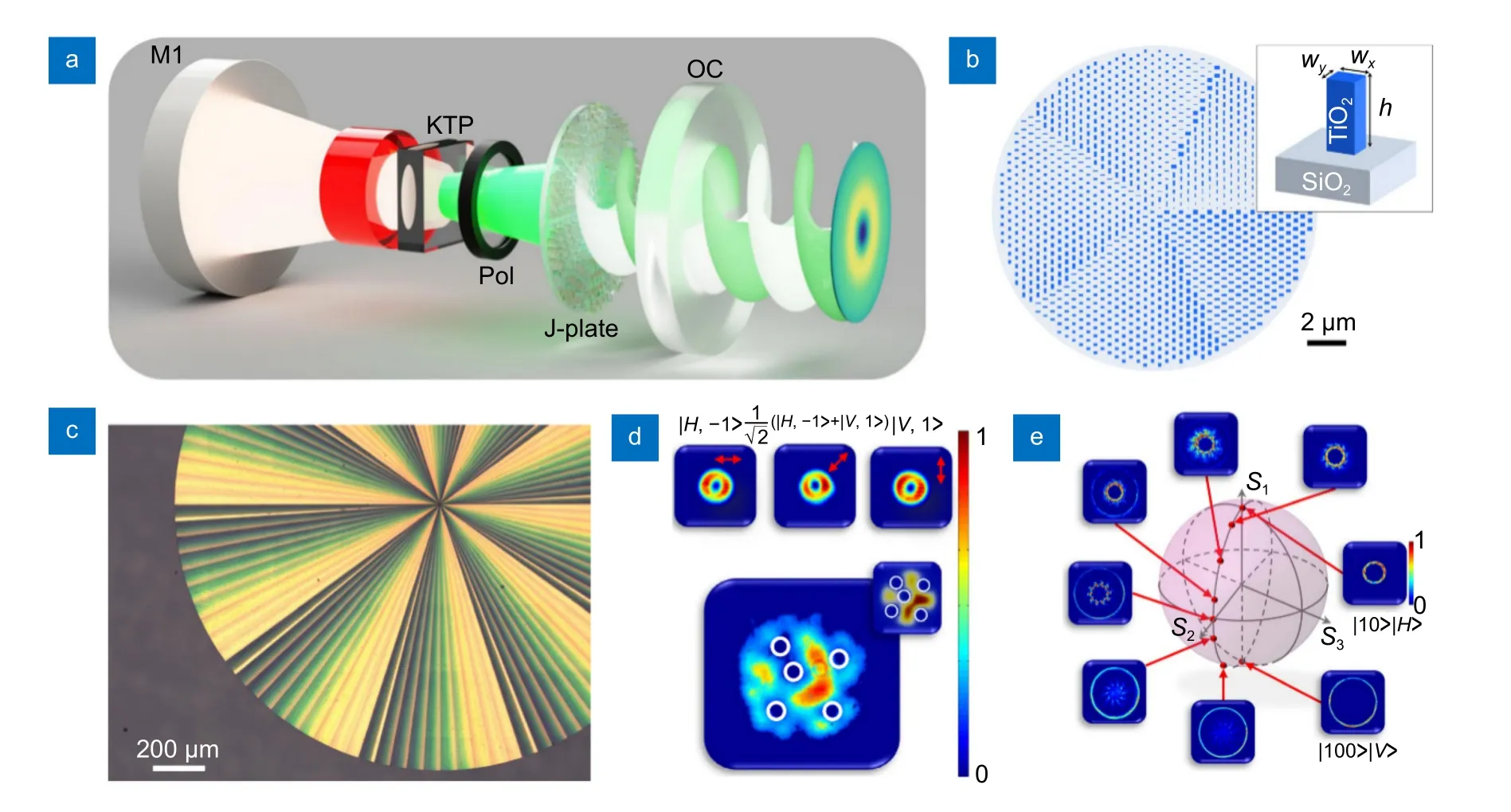
图1 一种基于TiO2 纳米柱的全介质超表面生成超手性高拓扑荷涡旋光束[65]。(a) 基于超表面转化的激光泵浦源及各部件示意图；(b) 超表面中心部位示意图与单元结构参数；(c)生成拓扑荷l1=10 与l2=100 涡旋光束超表面的光学显微镜照片；(d)旋转超表面实现不同拓扑荷光束生成与叠加电场强度示意图；(e)显示不同激光测量状态的广义OAM 球Fig.1 A dielectric metasurface based on TiO2 nanorods[65].(a) Schematic diagram of laser pumping source and components based on metasurface conversion;(b) Schematic diagram of the central part and unit structural parameters of the metasurface;(c) Optical microscope images of the generated metasurfaces with topological charge l1=10 and l2=100;(d) Schematic diagram of generating and superimposing electric field intensities of beams with different topological charges by rotating the metasurface;(e) Generalized OAM spheres displaying different laser measurement states

之前已经有许多研究提出使用几何相位(PB 相位)为圆偏振光赋予OAM，这种调制方式的实现原理不依赖于结构的尺寸变化，而是基于圆偏振光与具有各向异性的结构相互作用。利用单元本身的旋转为正交偏振赋予新的相位因子，大小为单元旋转角度的两倍，并且具有自旋相关特性[66-70]。近年来，人们发现高阶旋转对称单元中可以产生高阶的广义几何相位[71]。利用这种调制方式的超表面器件会转换入射圆偏振光的自旋角动量为OAM，反转极化手性特征，入射光的自旋角动量被转化为轨道角动量，其l总是保持一致，不能自由调控。Hend Sroor 等人将几何相位与传输相位相结合。传输相位通过调节结构尺寸进行调控，相位累积与自旋无关，并且在设计时调控的参数独立于PB 相位理论。因此，可以为入射光的任意两个正交偏振态赋予不同l值的轨道角动量，打破固有的手性限制，使得超表面生成涡旋光束的通用性与实用性大大增加。图1(c)所展示的超表面能够将水平和垂直偏振光分别转化为OAM 拓扑荷l1=10 与l2=100 的涡旋光束，不仅具有超手性，也能高效地实现高拓扑荷光束生成。超表面的手性特征在涡旋光方面的体现是在正交圆极化光束入射时的自旋耦合特性。即单纯基于PB 相位理论设计的超表面在左旋圆极化光入射时产生的涡旋光拓扑荷数，会和右旋圆极化入射产生的涡旋光拓扑荷数互为共轭。而超手性是指在正交圆极化光入射时，突破原有的手性限制，产生非共轭的一对拓扑荷，实现自旋解耦的特性。图1(d)为生成任意矢量叠加状态的相干混合涡旋光，生成传统共轭OAM 光束的超表面在旋转过程中的光强保持不变，始终为环形强度分布，拓扑荷数由正转负。而非对称OAM 模式的光束在超表面旋转时产生了矢量叠加，该超表面能够生成的拓扑荷值为l1=1 与l2=5，光强呈现5 个中心涡旋。在对拓扑荷差值不大的情况进行研究后，他们还对极端非对称情况进行了探究，在拓扑荷差值高达90 的情况下对超表面进行旋转，得到的结果如图1(e)所示。在这个广义庞加莱球中，北极为l1=10 的OAM，南极为l2=100 的OAM，其他情况为从北极至南极的变化，光强由小空心环逐渐变为双空心环，再到大空心环，这可以理解为每一种OAM 模式都在发光，但在超表面之后占据不同的空间。这种超表面的提出将OAM 激光器与片上器件研究相结合，为从光源处自由控制角动量提供了新的路线。

尽管涡旋光束的应用广泛，但是其环形光强分布与拓扑荷数密切相关。随着拓扑荷数的增加，光环半径产生变化，涡旋光束中心相位奇点处偏振态不稳定，强度分布崩溃，使得不同模式的涡旋光束分布不能保持一致，同时多模态复合传输与整体光束的半径受到约束[72-75]。多个OAM 耦合到单个光纤中进行多模态传输、高拓扑荷光束无法匹配光纤半径等，都是涡旋光束应用受到的限制。为解决这些问题，完美涡旋光束(PVBs)应运而生，其环半径恒定，不再受拓扑荷数变化的影响[76-78]。此外，进一步的研究提出了完美矢量涡旋光束(PVVBs)，为涡旋光束的应用开拓了更加广阔的前景。矢量涡旋光束(Vector vortex beam)是在涡旋光束的基础上进一步发展出来的新型光束类型，除了涡旋相位的存在，矢量涡旋光束还具有不同偏振分布，包含圆偏振、线偏振和椭圆偏振[79-82]。相比于单一的涡旋光束，矢量涡旋光束具有更加复杂的光场分布和波前结构，在光学显微成像、光学加工和量子信息等领域具有重要应用。此外，矢量涡旋光束还可以被视为光学中的自旋光束，与电子自旋和原子自旋有类似之处，因此在光学理论研究和量子光学等领域也有着广泛的研究兴趣。不同于简单的涡旋光束只能描述空间旋转对称性的光学现象，矢量涡旋光束更加复杂的波前结构不仅包含了空间旋转对称性，还包含了涡旋角动量所代表的自旋量子数，具有更加多样的光学性质和应用前景[7,83-85]。2020 年，Bao 等人设计了一种单层全介质超表面，用独特的单元设计对控制光束偏振与相位的灵活度进行了研究，能够在圆极化光法向入射时实现完美涡旋光束的生成，在线性偏振斜入射的情况生成完美矢量涡旋光束，为产生更加复杂的涡流场提供了更多的可能[61]。

Bao 等人指出，不同矢量涡旋光束(VVB)的产生可以看作是由两个正交圆偏振涡旋的线性组合，即:

Rm和Ln分别为具有m和n阶拓扑荷的涡旋光，ex和ey为 笛卡尔坐标系两轴正交单位向量，(θ,φ0)为庞加莱球上球面坐标，引入l0=(m-n)/2为偏振阶，lp=(m+n)/2为拓扑荷，用于描述如图2(a)所示庞加莱球上赤道处线偏振矢量涡旋光束的特性，并将其引申至任意极化状态。可以看到，传统涡旋光束在球面上的变化会带来光强环半径的改变，而完美矢量涡旋光束的光强环带在任意模态下都保持一致。

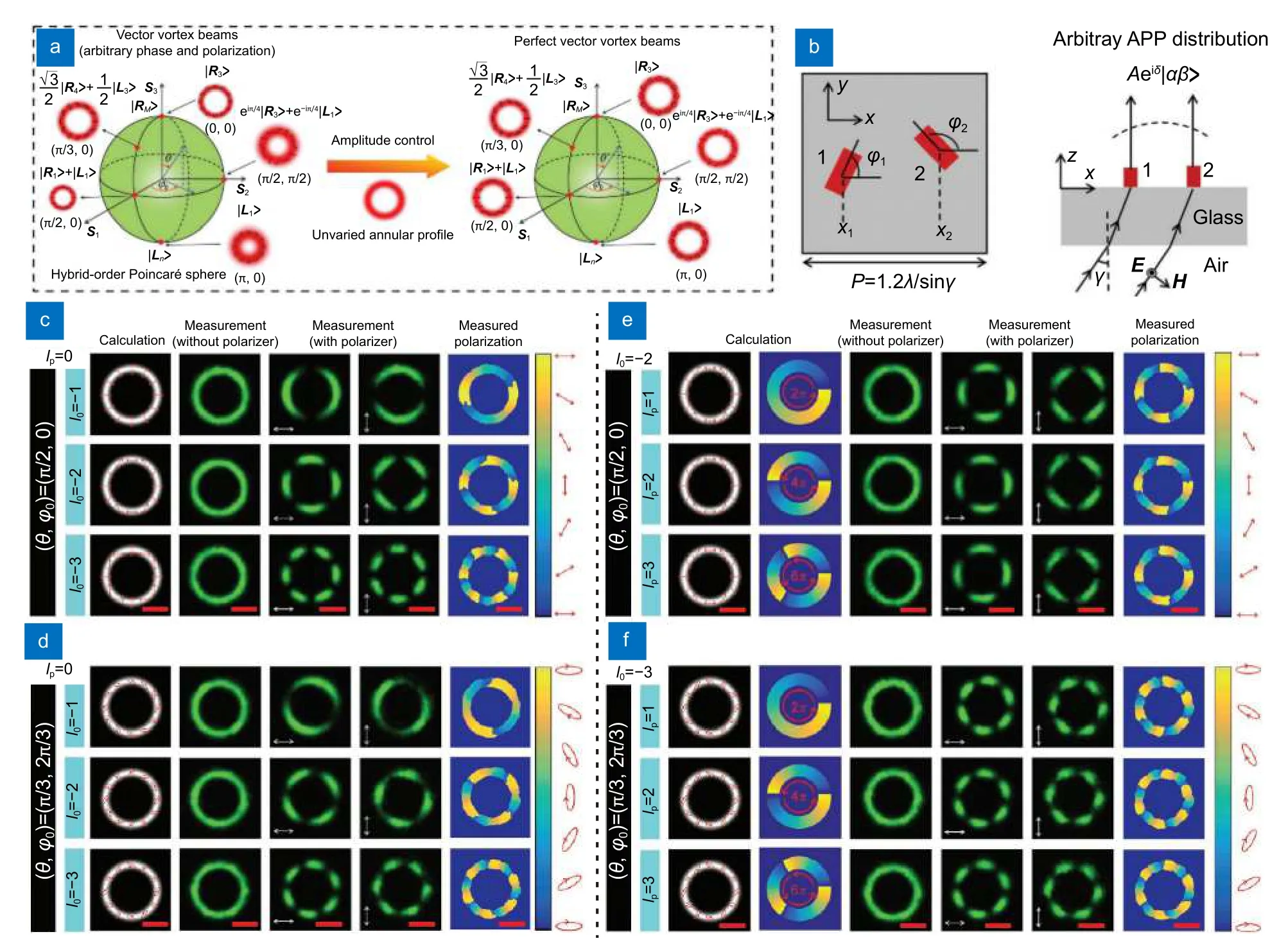
图2 基于双晶体柱单元的全介质超表面生成具有不同偏振矢量特性的涡旋光束[61]。(a)传统矢量涡旋光束与完美涡旋矢量光束的庞加莱球表示,包含不同球坐标理论强度分布与偏振态分布示意图。(b)双硅晶体柱单元结构示意图与斜入射实现入射波波前相位、振幅与偏振态调制示意图。(c) (θ,φ0)=(π/2,0),lp=0 时不同l0 的理论强度分布,偏振态分布以及实验测得的强度分布和偏振分布,包含经过正交偏振片后的强度。(d) (θ,φ0)=(π/3,2π/3),lp=0 时不同l0 的理论强度分布,偏振态分布以及实验测得强度分布和偏振分布,包含经过正交偏振片后的强度。(e) (θ,φ0)=(π/2,0),l0=-2 时不同lp 的理论强度分布,偏振态分布以及实验测得的强度分布和偏振分布,包含经过正交偏振片后的强度。(f) (θ,φ0)=(π/3,2π/3),l0=-3 时不同lp 的理论强度分布,偏振态分布以及实验测得强度分布和偏振分布,包含经过正交偏振片后的强度Fig.2 Metasurfaces based on dual crystal pillar unit cell [61].(a) Poincaré sphere representation of a conventional vector vortex beam and a perfect vortex vector beam,illustrating their different theoretical intensity and polarization distributions in spherical coordinates;(b) Schematic of the bilayer silicon pillar unit structure and the modulation of the incident wavefront phase,amplitude,and polarization state under oblique incidence;(c) Intensity and polarization distributions obtained from theory and experiment for different l0 values at (θ,φ0)=(π/2,0) with lp=0,including the intensity after passing through an orthogonal polarizer;(d) Intensity and polarization distributions obtained from theory and experiment for different l0 values at (θ,φ0)=(π/3,2π/3) with lp=0,including the intensity after passing through an orthogonal polarizer;(e) Intensity and polarization distributions obtained from theory and experiment for different lp values at (θ,φ0)=(π/2,0) with l0=-2,including the intensity after passing through an orthogonal polarizer;(f) Intensity and polarization distributions obtained from theory and experiment for different lp values at (θ,φ0)=(π/3,2π/3) with l0=-3,including the intensity after passing through an orthogonal polarizer

显然，想要使矢量涡旋光束具有恒定的环带光强分布需要对入射光的偏振、振幅、相位这三个量都进行调控，因此提出了一种具有双纳米柱单元的结构，每个单元由两个相同的硅晶体纳米块组成，两者独立旋转，分别为如图2(b)所示的 φ1和 φ2，长轴长度为105 nm，短轴为40 nm，高度为600 nm，衬底材质为二氧化硅，工作波长在532 nm。除了两个硅纳米块各自的旋转角度，还可以调控一个单元内两个柱各自的位置X1和X2，同时，从衬底斜向入射的光又引入了一个新的可调谐变量，即入射光波矢量与衬底表面法向轴的夹角 γ。对这五个变量进行选择实现对入射波振幅、相位和偏振的调控，γ的引入使得周期P的大小与其产生了如图所示的线性关系。图2(c)和2(d)是lp为零时具有不同l0和 (θ,φ0)的完美矢量涡旋光，图2(c)中的偏振态为线偏振，对应的l0已经标出，第一列为理论强度分布和偏振态分布，第二列为实验测量得到的强度分布，第三列和第四列则是通过一对正交偏振片后的光强分布，第五列为测量得到的偏振方向和分布。可以看到在相同的偏振态下，不同l0对应的光环半径几乎保持一致，经过偏振片后的强度也足以验证确实发生了l0的改变。图2(d-f)与图2(c)类似，图2(d)为椭圆偏振态情况下的对比。图2(e)和2(f)侧重于比较完美矢量涡旋光束与lp的相关性，第二列是计算得到的拓扑荷相位项lpφ。可以看到，无论l0与lp如何变化，光强总能保持恒定大小，为涡旋光束的实用性研究做出了贡献。

庞加莱光束是由法国数学家庞加莱提出的椭圆偏振光束，其椭圆偏振的方向具有时间周期性变化，也就是说沿着光束传播方向的椭圆偏振方向会发生旋转。庞加莱光束具有重要的应用价值，在光学成像等领域都有着广泛的应用。在此基础上进行衍生，2021 年，Liu 等人提出的全介质超表面可以在宽带范围生成更加复杂的完美高阶庞加莱光束(PPBs)[86]。

高阶庞加莱光束是一种特殊的光束模式，其相位结构在横截面上呈现出螺旋形状。它是庞加莱球面波的高阶模式，也被称为光学螺旋波前(optical vortex wavefront)。高阶庞加莱光束的相位结构具有较高的复杂度，通常由较高阶的光场模式组成。与普通的庞加莱光束相比，高阶庞加莱光束具有更复杂的相位结构和更高的光场模式数。这些光场模式可以通过在光束传播方向上引入不同的相位和幅度分布来实现。我们同样可以通过庞加莱球来描述各种混合阶PPB，即混合阶庞加莱球(HyOPs)，如图3(a)所示。HyOPs 的两极为具有相同椭圆度和不同相位拓扑荷的完美涡旋光束，分别是lm=5 和ln=5。随机选择了球体的六个坐标，这六种具有不同偏振椭圆度和拓扑荷的完美庞加莱光束依然保持恒定的光强环半径，图中还展示了使用垂直线性偏振片将这些光束转换后的图案。

图3 一种全介质自旋复用超表面实现多种完美庞加莱光束[86]。(a)各种完美庞加莱光束的混合阶庞加莱球表示；(b)由布置在熔融二氧化硅基板上的TiO2 矩形纳米柱构成的超表面示意图，包含单元的透视图与俯视图；(c)超表面相位叠加方法示意图；(d) 530 nm 工作波长下y-z 平面上光学涡旋强度分布于焦点处x-y 平面光学涡旋环形强度分布图，比例尺10 μm，右侧为MF1 与MF2 环形强度分布归一化截面图；(e) 480 nm (蓝色)、580 nm (黄色)、630 nm (红色)波长下y-z 平面光强归一化分布与焦点处光强归一化分布，比例尺10 μmFig.3 A kind of all-medium spin-multiplexing metasurfaces for various perfect Poincaré beams[86].(a) Hybrid-order Poincaré sphere representation of various perfect Poincaré beams;(b) Schematic view of the metasurface composed of rectangular TiO2 nanorods arranged on a melted silica substrate,including perspective and top views of a unit cell;(c) Schematic diagram of the phase superposition method of the metasurface;(d) Intensity distribution of optical vortex in the y-z plane at the working wavelength of 530 nm,and the ring-shaped intensity distribution of optical vortex in the x-y plane at the focal point,with a scale of 10 μm.The right side is the normalized cross-sectional distribution of the ring-shaped intensity of MF1 and MF2;(e) Normalized light intensity distribution in the y-z plane at 480 nm (blue),580 nm (yellow),and 630 nm (red) wavelengths,and the normalized light intensity distribution at the focal point,with a scale of 10 μm

全介质超表面可以实现更好的片上集成，整体结构更加小型化和轻量化，能够更好地集成到紧凑的纳米光子平台中，同时将传统生成方式复杂光路简化，使得现有光路能够更好地准直，减少相差。图3(b)展示了构成超表面的单元和超表面的示意图，是在二氧化硅衬底上构建的TiO2长方柱结构。每个单元以相同周期U分隔，U恒定为450 nm 以保证整体阵列等效为零阶光栅。为了实现完美庞加莱光束的生成，将传输相位与几何相位的调制原理相结合，形成相位层面的叠加，实现自旋复用功能。具体叠加方式如图3(c)所示，对长轴和短轴的调控为入射光束的x与y分量分别赋予相移 δx和 δy，将大小不一的纳米柱进行像素化阵列排布，完成第一层叠加相位的分布调制，能够为正交分量分别引入相位分布φ1和 φ2，以产生不同完美涡旋。旋转柱结构会为入射的圆极化光赋予与旋转角度θ成线性关系的附加相位，不同旋转角度的柱阵列赋予了入射波第二层相位调制。将二者叠加可以实现完美庞加莱光的相位需求，为了完成叠加，传输相位调控所寻求的所有柱都应等效于半波片，即δx和 δy的差值始终恒定为π，但不同柱之间仍然应该存在相位梯度。这两种调制均为相位调制，不涉及幅度调制。

文中共设计了两种超表面，尺寸为90 μm×90 μm，其中一号超表面(MF1)为右旋圆极化光转换的拓扑荷数lm=1 的涡旋光束与左旋圆极化光转化的拓扑荷数ln=5 的涡旋光束叠加，而二号超表面(MF2)则是lm=5 与ln=10 涡旋光束的叠加。具体的实现思路是利用正交圆极化光自旋复用特性在单一超表面生成具有不同拓扑荷数的完美涡旋光束并进行叠加，生成结果如图3(d)所示，对于两种超表面生成的所有模态完美庞加莱光束在焦点处光强环半径几乎都保持一致，其截面归一化强度分布曲线也印证了这一点。图3(e)则是两种超表面在不同波长情况下的工作状态，波长的改变会使得保证环半径一致的焦距发生变化，对应于480 nm (蓝色)、580 nm (黄色)、630 nm (红色)波长的传播距离z=230 μm、195 μm 和180 μm，尽管焦距发生了改变，但仍然能够在宽带范围实现混合阶完美庞加莱光束的生成。利用具有高空间分辨率的单层全介质超表面生成庞加莱光束，可有效地生成和控制结构化光束。这种方法可以进一步提高对入射波的波前相位的灵活调控，并促进其在实际应用中的推广，例如光学通信、光学加密、量子信息科学等方向。

之前已经利用全介质超表面实现了多种矢量光束的生成，但利用超表面的设计自由度与高集成特性还可以为矢量光束赋予更多有趣的功能，比如三维矢量光场的调控研究[87-88]。2022 年Zheng 等人提出的超表面可以在太赫兹波段产生纵向变化的矢量涡旋光束，在光束传播的方向上进行不同矢量涡旋光束的集成[89]。超表面转化的光束为具有涡旋相位的拉盖尔-高斯光(Laguerre-Gaussian beam)[90]。文中涉及的超表面充分利用了传播的两个自由度和几何相位，可以灵活的控制两个正交圆偏振态的场分布。为了在波矢传播方向(z方向)实现随距离变化的矢量光束集成，主要的设计理念是在纵向上叠加两个具有不同焦距的涡旋光束，这得益于对超表面进行相位设计可以实现平面透镜，即超透镜。将超表面分为两个部分，中心圆形部位叠加有近焦距f1会聚超透镜相位分布，圆形部位以外的环形区域同样叠加有会聚相位分布，能够在更远的焦距f2进行会聚，为这两个区域附加上不同的涡旋相位，可以在纵向上实现两个涡旋的叠加，随着空间相位的变化而变化。

首先是对左旋圆极化光的转化，具体来说，在近焦处(焦距f1=4000 μm)，超表面透镜可以汇聚拓扑荷为l=+2 的涡旋光束；而在远焦点(焦距f2=6000 μm)处，同样可以汇聚具有拓扑电荷l=-2 的涡旋光束，这个过程在图4(a)中有所展示。另一方面，图4(b)所示为光强度变化与相位变化图。在距离从z=4000 μm 到z=4500 μm 的范围内，涡流场主要由拓扑荷为l=+2 的涡旋组成。而在距离从z=4500 μm 到z=5500 μm 的范围内，涡流场的拓扑荷为l=+2 和l=-2 的涡旋都比较明显。随着距离的增加，拓扑荷为l=-2 的涡旋逐渐占主导地位。在最后的500 μm 的范围内，涡流场主要由拓扑荷为l=-2 的涡旋组成。针对右旋圆极化光入射，其所生成的涡旋光场分量显示出了相似的演化趋势，即从拓扑荷为l=+1 的主导涡流到拓扑荷为l=-1 的主导涡流。这种演变趋势是高度聚焦系统中自旋到轨道角动量转换的结果，即通过超表面透镜将光转化为纵向偏振涡旋束的同时，相应的拓扑荷的变化也呈现出了相同的趋势，如图4(c)和4(d)所示。

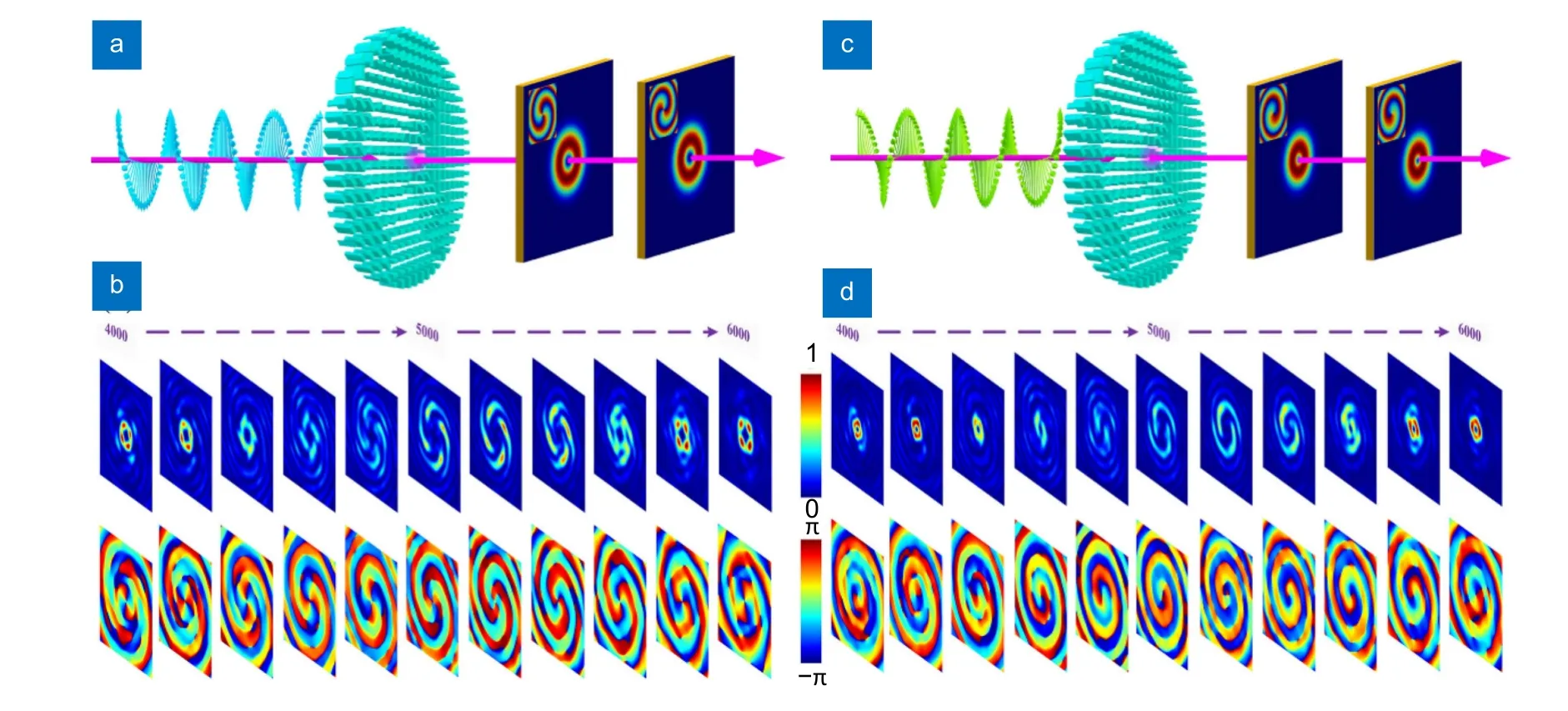
图4 圆极化入射全介质超表面生成拓扑荷数空间纵向变化的涡旋光[89]。(a)左旋圆极化光入射超表面时在纵向集成拓扑荷l=±2 的涡旋光束；(b)随着传播距离变化的空间场强分布截面与相位分布(x-y 平面，左旋圆极化入射情况)；(c)右旋圆极化光入射超表面时在纵向集成拓扑荷l=±1 的涡旋光束；(d) 随着传播距离变化的空间场强分布截面与相位分布(x-y 平面，右旋圆极化入射情况)Fig.4 Vortex beams with longitudinal variation in topological charges based on all-dielectric metasurfaces at the incidence of circular polarization[89].(a) Vortex beams of longitudinal topological charge l=±2 are generated when left-handed circularly polarized light is incident on the metasurface;(b) The spatial distribution of the field strength and phase changes with propagation distance in the x-y plane when lefthanded circularly polarized light is incident;(c) Vortex beams of longitudinal topological charge l=±1 are generated when right-handed circularly polarized light is incident on the metasurface;(d) The spatial distribution of the field strength and phase changes with the propagation distance in the x-y plane when right-handed circularly polarized light is incident

对于两个具有相反拓扑电荷的拉盖尔-高斯光的叠加，其表达式可以表示为

其中：cl为LG 光的系数，l为涡旋光束携带的拓扑荷数，φ为方位角。可以从式(3)中看出光束叠加产生了具有径向偏振特性的矢量光束。如果为这两束涡旋光之间引入数值为π 的相位差，则表达式转变为

在这种情况下则产生了角向偏振分布的矢量光束。通过涡旋光的叠加可以生成矢量涡旋光，线偏振光束也可以分解为一对正交圆极化光，因此在之前两种超表面的设计基础上，可以更进一步地研究线极化光束入射产生具有纵向变化的矢量涡旋光束，如图5(a)所示。

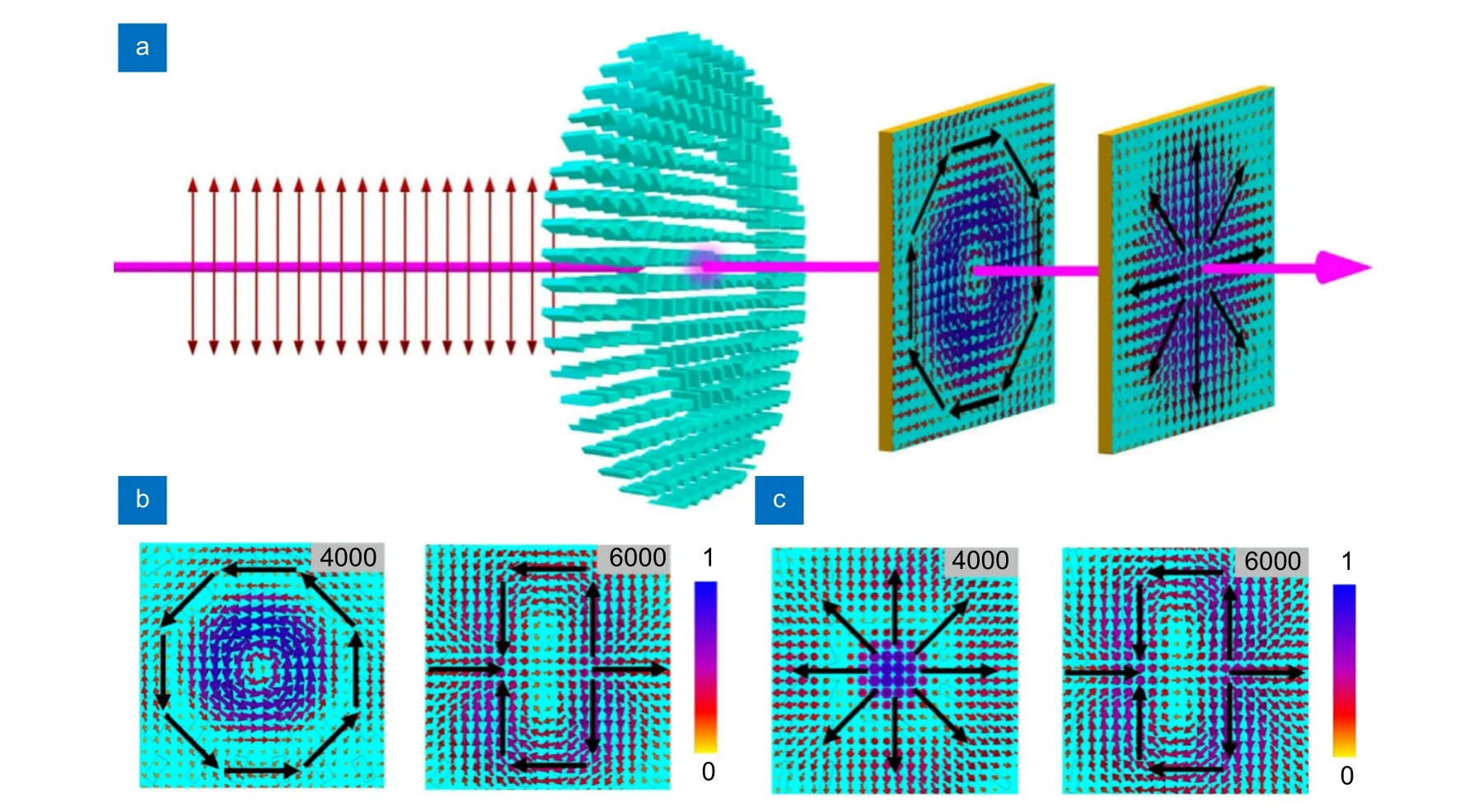
图5 线极化入射超表面生成矢量涡旋光[89]。(a)入射光在z 方向由角向偏振分布涡旋光束向径向偏振分布涡旋光束转化；(b)空间偏振分布，从角向分布到二阶径向分布；(c)空间偏振分布，从径向分布到二阶径向分布Fig.5 Vector vortex beam generation at the incidence of linear polarization[89].(a) The incident light polarized in the z-direction is converted from a vortex beam with angular polarization distribution to a vortex beam with radial polarization distribution;(b) Spatial polarization distribution changes from an angular distribution to a second-order radial distribution;(c) Spatial polarization distribution changes from a radial distribution to a second-order radial distribution

图5(b)展示的是叠加两束具有相位差π 的LG 光产生的角向矢量涡旋光束的偏振变化，在4000 μm 处表现为标准的角向矢量偏振，而传播到6000 μm 处时，偏振特性变为二阶径向偏振变化。图5(c)则是没有相位差的光束的叠加，因此在近焦处呈现径向矢量偏振分布，在传播至远焦处时同样变为二阶径向分布。通过这一系列超表面设计模拟与实验验证，产生了在纵向上灵活变化的矢量涡旋光束，充分利用了光偏振传播特性和超表面自身的设计自由度，为矢量光的产生提供了更多方向。

3 金属型超表面生成涡旋光束

金属超表面是由具有亚波长尺寸的二维金属单元构成的平面结构，具有可调制的光学特性[91-93]。它们被广泛应用于光学设备、传感器[94]、信息显示和通信等领域。通常，金属超表面的单元是由金属(例如银、铝、金等)制成，并沿着一个平面排列[95-99]。每个单元的大小通常小于光波长，因此可以被当作一个整体来处理，其表现形式与整个表面的光学反应相关。可以通过调整每个单元的几何形状、尺寸和分布方式，实现对光学性质的有效控制，如偏振[100-101]和相位等。金属超表面的光学性质可以通过控制光的透射、反射和吸收来实现[102-104]。可以调整金属超表面的结构，使其吸收或反射特定波长的光，实现类似于滤波的功能。此外，金属超表面还可以实现类似于透镜和棱镜的功能，通过对光的相位进行调整实现光的聚焦、分束和成像[105-106]。

由于金属超表面具有体积小、轻巧、灵活可控等特点，在光学应用领域中拥有广泛的应用前景。在介质超表面部分我们曾经提及利用双柱结构实现完美矢量涡旋光束的生成，双柱结构对于设计与加工还是具有一定的复杂性，早在2018 年，Zhang 等人提出的金纳米孔阵列只利用PB 相位原理进行调控生成不同波长完美涡旋光束，虽然没有为涡旋光束赋予矢量偏振特性，但其设计思路与加工难度都更具有普适性[107]。如图6(a)所示，结构为正方形金板上的矩形孔，以法向为轴进行旋转，金纳米孔简单的构造可以使超表面的空间分辨率得到提升，使相位调制精度更加的精细，加工精度的提升也使得该结构能够更好地匹配PB 相位的调控模式，超表面的整体尺寸为50 μm×50 μm。对于PB 相位，矩形孔的旋转角度 θ与相位息息相关，图6(b)展示了不同旋转角度下相位的曲线，在600～1000 nm 波长范围内相位曲线变化均匀且平滑，容差非常高。传统方式实现完美涡旋光的光路由轴锥、螺旋相位板以及透镜完成，将三者的相位分布按照如图6(d)所示进行叠加，得到需要的相位，再通过旋转矩形孔进行阵列排布，使整个阵列的相位分布与设计需求符合。从图6(c)我们可以看到，在相同的波长条件下，不同纵向距离处光圈大小不同，但不同拓扑荷光圈的大小能够保持一致，对纵向传播方式进一步进行探索，如图6(e)所示，整个光束的能量几乎全部集中在光强环带上，整个光环随着传播逐渐扩散，可以通过调节纵向距离得到不同大小的光圈。如果深化相位的叠加，可以将不同拓扑荷的光斑集成在同一表面进行观察，如图6(f)所示，针对不同焦距设计得到不同的相位排布，可以在同一焦平面同时观察到四个大小一致但具有不同拓扑荷的圆环。介质型超表面也可以实现类似的功能，但金属超表面的制备更加容易。

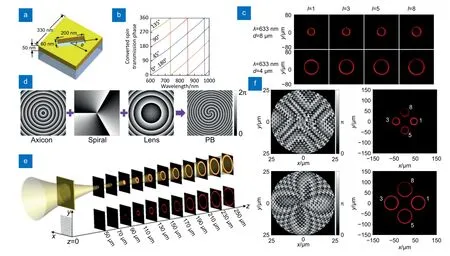
图6 金纳米孔阵列实现完美涡旋光[107]。(a)金纳米孔结构参数与示意图；(b)不同旋转角度对应的相位曲线分布；(c)相同波长下不同拓扑荷在不同纵向距离的光强对比；(d)实现完美涡旋光需要的相位叠加；(e)生成的完美涡旋光束光强纵向分布示意图；(f)同一焦平面实现四束完美涡旋光的相位分布于光强分布，上半部分焦距为4 μm，下半部分焦距为8 μmFig.6 Perfect vortex light generated by the gold nanopore array[107].(a) Structural parameters and schematic diagram of the gold nanopore;(b) Phase curve distribution corresponding to different rotation angles;(c) Comparison of light intensity of different topological charges at different longitudinal distances under the same wavelength;(d) Phase superposition required to achieve perfect vortex light;(e) Schematic diagram of the longitudinal distribution of the generated perfect vortex light beam intensity;(f) The phase distribution and light intensity distribution of four perfect vortex lights realized on the same focal plane,with a focal length of 4 μm in the upper half and 8 μm in the lower half

在矢量光束应用的研究中，高容量光通信始终是一个热门的课题，之前提及的研究更多集中在同轴传输光束复用，而离轴控制技术提及的并不很多。2021 年，Chen 等人提出了一种使用离轴偏振控制圆柱矢量波束的复用-解复用反射金属超表面，用以解决传统光纤光通信中波分复用的限制[108]。波分复用技术旨在同一光纤传输多路不同波长的光信号，实现多路信号的同时传输，从而提高了光纤带宽利用率，然而终究会受到带宽的限制，由于传输带宽可用性有限，使得传输速率最终会出现阈值。

有别于涡旋光束，圆柱矢量光束具有空间非均匀偏振，并不承载有光学角动量，其在大气湍流中具有强大的超长距离传输能力，这是由于矢量模是少模光纤的本征模，同时，其波长与偏振态无关[109-110]。但是，圆柱矢量光束可以由两个具有反向圆极化和共轭拓扑电荷的涡旋光束耦合而来，延伸至一般情况，具有第m偏振阶的圆柱矢量光束的Jones 矩阵可以表示为

其中：E0是简化振幅，m是偏振阶数，θ是方位角，φ0是初始相位。

为了方便地实现离轴操控，这里涡旋光束的生成不再是在平面上覆盖涡旋相位，而是利用Dammann涡旋光栅相位 (Dammann vortex grating phase)来实现[111]。Dammann 涡旋光栅是一种特殊的光学元件，通过在光栅表面设计特殊的相位结构，可以将入射的光束分成若干个光束，每个光束的相位结构都呈现出涡旋状的相位分布。相比传统的方法，使用Dammann 涡旋光栅可以更加高效地产生涡旋光束，而且可以产生多个涡旋光束并控制它们的位置和数量。具体来说，入射的波前通过光栅相位后会被分成多个相同的区域，并在每个区域中形成一个涡旋光束，如图7(a)所示，蓝色圆形箭头用于表示RHCP (righthanded circularly polarized)，红色箭头用于表示LHCP(left-handed circularly polarized)，当一束光入射时，会在四个区域生成不同的涡旋光束，单元结构的侧视图和俯视图在图7(a)右侧表示，超表面由多层结构组成，由上至下，厚度恒定为50 nm 的金矩形片结构沉积在二氧化硅上，下层是金膜与硅构成的金镜，增强反射效率。图7(b)是图7(a)中各个模式对应的光场分布图。要实现图中所示的功能，超表面x与y方向上的相位延迟符合图7(c)中所示的三个级别，且均为半波延迟，图7(d)则是LHCP 光束的三个不同取向角获得的相位延迟。

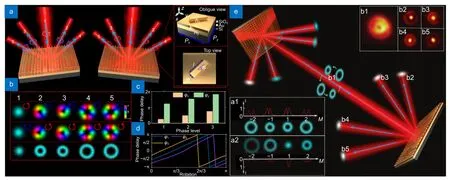
图7 金属超表面实现圆柱矢量光束的多路复用与解复用[108]。(a)不同光束入射金属超表面产生多衍射级不同拓扑荷涡旋光束；(b)入射光束与不同衍射阶光束的偏振态及光强分布示意图；(c)超表面在x 与y 方向满足三个级次的相位分布；(d)不同入射角度产生的相位延迟；(e)利用两个超表面实现多路复用与解复用示意图，包含入射光束、多路复用光束与阶复用光束的偏振与光强分布图Fig.7 Multiplexing and demultiplexing of cylindrical vector beams based on metal metasurfaces[108].(a) Metal metasurfaces generating multilevel diffracted topological vortex beams for different incident beams;(b) Schematic diagram of the polarization state and intensity distribution of the incident beam and different diffracted order beams;(c) The metasurface satisfies three order phase distributions in the x and y directions;(d) Phase delay generated by different incident angles;(e) Schematic diagram of multiplexing and demultiplexing using two metasurfaces,including the polarization and intensity distribution of the incident beam,multiplexed beam,and order multiplexed beam

为了实现圆柱矢量光束的多路复用，使用超表面对多路入射光束复用的同时，还需要另一个超表面对接受光束进行解复用，如图7(e)所示。将四束具有数字信号的高斯光束以不同的衍射级角度入射到复用器上，取决于不同的入射角度，所有高斯光束均被转化为具有不同偏振级数的圆柱矢量光束，与超表面的零级衍射进行同轴传输，完成发射信号的波前调制。一个能够生成m阶衍射级圆柱矢量光束的超表面可以用来进行信号的解调工作，设计方法与之前类似且更加简单。除了单纯的高斯光束入射，也可以使用不同m的圆柱矢量光束进行入射，例如入射m=-1的圆柱矢量光束，图7(e)中的a1 是高斯光束入射时4个衍射级中的偏振与强度分布，a2 则是以m=-1阶的圆柱矢量光束入射时的衍射级强度与偏振分布，是衍射级为+1 的高斯光。多路复用的同轴光束与多路分解，即b1～b5 的实验光强也在图7(e)的右上角标出。由于金属超表面平坦紧凑，因此在系统集成和小型化方面非常有前景，可以在高容量通信系统中得到应用。

和介质型超表面相比，金属超表面更加平面化，利用其平坦特性进行集成可以为超表面生成涡旋光束赋予更多的可能性，如2020 年Zhao 等人提出的利用金属超表面实现高效率二次谐波涡旋光束的产生，就是将非线性材料与金属超表面相结合，以产生谐波涡旋束[112]。所谓二次谐波，是指在非线性光学过程中产生的一种光波。当一束高功率的激光束通过一些非线性光学介质(如晶体、光纤等)或者表面，会发生非线性光学效应，导致在输出光波中产生频率是输入光波频率的两倍的波，即二次谐波。二次谐波的频率是输入光波频率的两倍，因此它的波长是输入光波波长的一半。二次谐波涡旋光束可以在谐波频率下具有螺旋相位面，同样可以提供额外的复用自由度和信息编码能力。

为了实现上述功能，该论文主要利用的是单层金属超表面的小宽深比，在金属板上打孔，使得制备出的超表面可以被视为基底进行二次加工。利用化学气相沉积法将一层WS2沉降在金纳米孔阵列表面，这一想法的实现充分利用了金超表面的稳定与平坦，以金纳米孔阵列激发具有涡旋相位分布的出射场，对覆盖于表面的WS2进行泵浦足以生成具有增强转换效率的非线性OAM 信号，如图8(a)所示。图8(a)左侧展示的矩形金纳米孔利用了PB 相位原理，在入射的LHCP 光束激励下产生带有拓扑荷l附加相位的右旋分量与不带涡旋相位的左旋分量，再经过单层WS2后变为了具有2l相位的LHCP 分量，RHCP 分量不再考虑，因此整体的变化如图8(a)右侧所示，根据谐波级次n的不同，最终的涡旋光束会带有2nl的拓扑荷。图8(b)的左侧为金纳米孔在时域有限元差分法模拟下的透射光谱，可以看出在810 nm 波长处有明显谐振峰值，右侧则是Au-WS2与单纯WS2光谱的对比，可以看到在405 nm 谐振处Au-WS2超表面的强度几乎达到WS2的4 倍，有明显的增强效果，且波长为基本波长的一半，确实为二次谐波响应。

图8 一种金属超表面实现二次谐波涡旋光束[112]。(a)金纳米孔阵列沉降WS2 层对光束的转化原理示意图；(b)金纳米孔阵列，Au-WS2 超表面以及单WS2 的透射谱分析；(c)超表面相位与空间传输示意图；(d)不同拓扑荷光强与相位分布图Fig.8 A metal metasurface achieving second harmonic vortex beams[112].(a) Schematic illustration of the transformation principle of the gold nanohole array settling WS2 layer on the beam;(b) Transmittance spectra analysis of the gold nanohole array,Au-WS2 metasurface,and single WS2;(c) Metasurface phase and spatial transmission schematic;(d) Distribution of different topological charges,light intensity,and phase

如图8(c)所示，金纳米孔阵列不仅有l=1/2的涡旋相位，同时叠加了聚焦相位，这是由于聚焦功能的引入可以使二次谐波焦点处的强度增加。同时，由于PB 相位原理，出射光束携带有与基本光束正交极化的信号，这一部分不带有相位信息，聚焦的引入增大这一部分在传播中的扩散，进一步提高了信号与背景噪声的比率。可以看到生成的信号在z轴传播的采样，由发散，到聚焦，再到扩散，成功的在焦点处形成明亮的圆环。在低拓扑荷成功实现的基础上，继续增大金纳米孔阵列的基础拓扑荷，从而实现了高达l=28的二次涡旋谐波，如图8(d)所示。每一种拓扑荷都包含了焦点处光强分布，对焦点的偏振检验以及焦点处相位的分布，在提高拓扑荷的同时保有高转化效率，证明了金属超表面转化的角动量可以投影在非线性材料的谐波信号上，为产生用于光通信的谐波光学涡旋提供了一条新的途径。

在光通信中除了利用矢量光束进行复用，矢量光束本身复杂分布的偏振态也为加密提供了可能。偏振是电磁波的一个基本特征，由于调制的矢量光可以同时包含多种偏振状态，能够传递大量的光学信息。2023 年，Zhao 等人提出了一种太赫兹波段的三层金属超表面，能够高效地进行矢量场的调控，利用单个超薄超表面为多通道光通信进行光学信息的携带与加密[113]。如图9(a)所示，超表面单元共有五层，单元表面和底部为一对正交的金属光栅结构，中间则是C形开口环，正交光栅用于实现偏振的转化，开口环调节相位变化。为了实现不同角度偏振态，光栅结构与x轴以 θ 和 θ+π/2 的角度进行旋转，控制金属光栅的缝宽和光栅条宽度进行调谐，对C 形开口环则是调谐其开口角度、内外圈环半径和旋转角度以实现相位的覆盖，相对于光栅，开口环的旋转为 +π/4。通过这三层结构的配合可以输出具有相位调制的不同角度偏振态光束。以多层金属单元为基础构建超表面，为了实现多通道输出，将超表面按照图9(b)所示划分为八个超级单元，每个大单元单独进行相位和偏振调制，在保证区块偏振态一致的情况下，利用基于瑞利-索末菲衍射理论的模拟退火算法进行迭代计算，得到每个区块的全息相位分布。

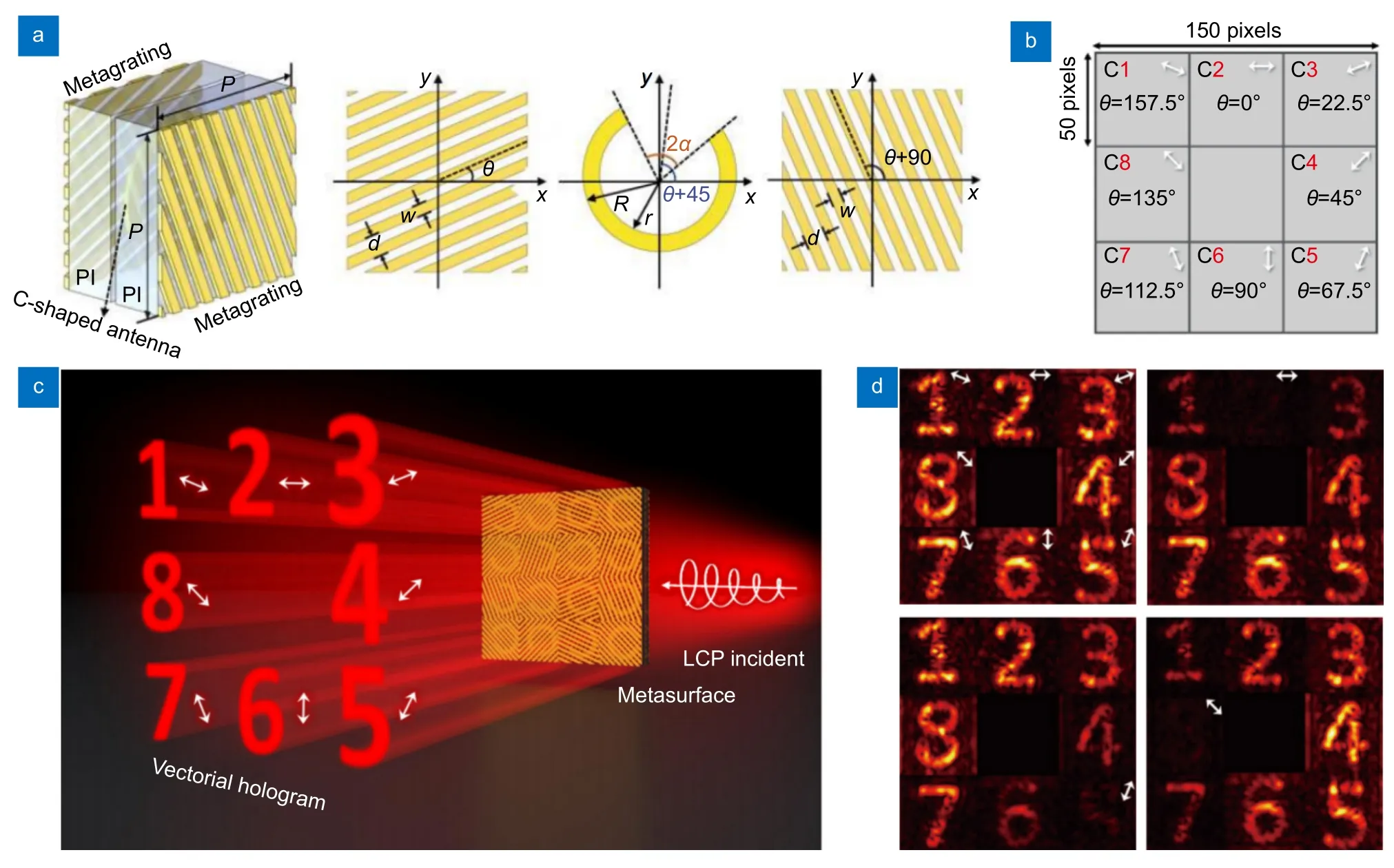
图9 一种三层金属超表面实现多通道矢量全息[113]。(a)三层金属超表面单元结构示意图，每层金属结构之间以PI (聚酰亚胺)介质隔开；(b)超表面阵列区块偏振旋转角度分布示意图；(c)超表面实现多通道矢量全息效果示意图；(d)实验结果示意图，包含没有选择偏振态进行检测的全息图振幅分布与不同通道隐藏偏振态实验振幅分布Fig.9 A three-layer metal metasurface realizing multi-channel vector holography [113].(a) Schematic diagram of the three-layer metal metasurface unit structure,with PI (polyimide) medium separating each layer of metal structure;(b) Schematic diagram of the polarization rotation angle distribution of the metasurface array blocks;(c) Schematic diagram of the multi-channel vector holography effect achieved by the metasurface;(d) Schematic diagram of the experimental results,including the amplitude distribution of the hologram without selecting the polarization state for detection,and the amplitude distribution of the experiment with different channels hiding polarization states

超表面的效果示意图如图9(c)所示，当一束圆偏振光入射时，每个区块分别生成了从一到八的全息图，且每个数字携带的偏振信息均不相同，整个波平面的偏振呈现非均匀分布。如果对某种偏振态进行滤波则可以实现矢量全息图的隐藏，如图9(d)所示。不进行偏振隐藏时，所有数字的全息影像都清晰可见，选择性地对某种偏振态进行滤波，对应的数字就会得到隐藏。

以上功能的实现都是依赖于金属超表面的超平坦特性，与介质超表面相比，这种方式无疑使单一超表面上不同结构的集成更加灵活，尽管金属超表面的损耗往往会大于全介质型超表面，但是在可接受的范围内也能为超表面实现多样化矢量光场的生成与应用提供全新的思路与方向。

4 智能超表面生成涡旋光束

目前对超表面的研究中，如何实现电磁波动态调控一直是研究的热点。目前，研究人员已经提出了多种可调谐超表面的设计方案和制备方法，例如，通过调节超表面中的电子、光子或声子耦合效应，可以实现对电磁波频率的调谐。此外，利用外加电场、热控、光控或化学反应等方法，也可以实现对超表面的调控[114-116]。在这里，我们着重介绍智能超表面。智能超表面是一种基于微结构和可编程元件的超表面，它可以根据需要对电磁波进行复杂的、高精度的调控，根据调控方式的不同，智能超表面也可以被称为可重构超表面、可调谐超表面或可编程超表面[117-121]。与传统的超表面相比，可编程超表面可以更加灵活地实现多功能调控，同时能够处理更具挑战性的光子学任务。除了在表面上对微小结构的三维形貌、大小、密度、分布等多种因素的参数化设计，可编程超表面的核心是可重构元件技术，它是可编程超表面的实现基础，亚波长电磁结构材料的电磁特性主要由结构的电磁响应决定，在单元结构中加载可调的电子元器件或者介电材料，包括MEMS 器件、液晶器件、电磁器件、光学器件等多种可编程元件，可以实现分别控制可编程超表面单元中微结构的不同状态[122-124]。这些状态包括振幅、相位、极化等，也可以是几个维度加和而成的多自由度状态，从而提高了超表面的可编程性和调控能力。能够看出，可编程超表面具有非常高的自由度，可以实现复杂、多功能的电磁波调控。同时，它还可以在新型传感器、智能表面、3D 成像、通信系统等许多领域中发挥巨大作用，它为光电子学领域的应用提供了全新的机会和解决方案，有着非常广阔的应用前景[125-127]。

目前实现可编程超表面的典型方法是使用PIN 二极管或变容二极管，如2020 年Li 等人提出的一种可编程散射超表面[128]，在单元中引入PIN 二极管，可以使得单元获得两种状态表征，主要是在相位上实现π的差值以形成“0”、“1”编码，再通过现场可编程逻辑门阵列(FPGA)进行数字控制，使超表面阵列能够在不同的编码模式下切换，从而实现功能的切换，如图10(a)所示。向超表面的PIN 二极管施加控制电压来动态控制相位、振幅和偏振态的反射系数，PIN二极管由FPGA 进行切换，FPGA 根据时空编码矩阵控制电路，从而控制PIN 二极管的关断。基于FPGA和PIN 二极管的控制电路，超表面实现了交叉线偏振(CLP)、右旋圆偏振(RHCP)和左旋圆偏振(LHCP)转换、散射操纵、扩散、双频带辐射、低交叉偏振发射和OAM 生成等多种功能。

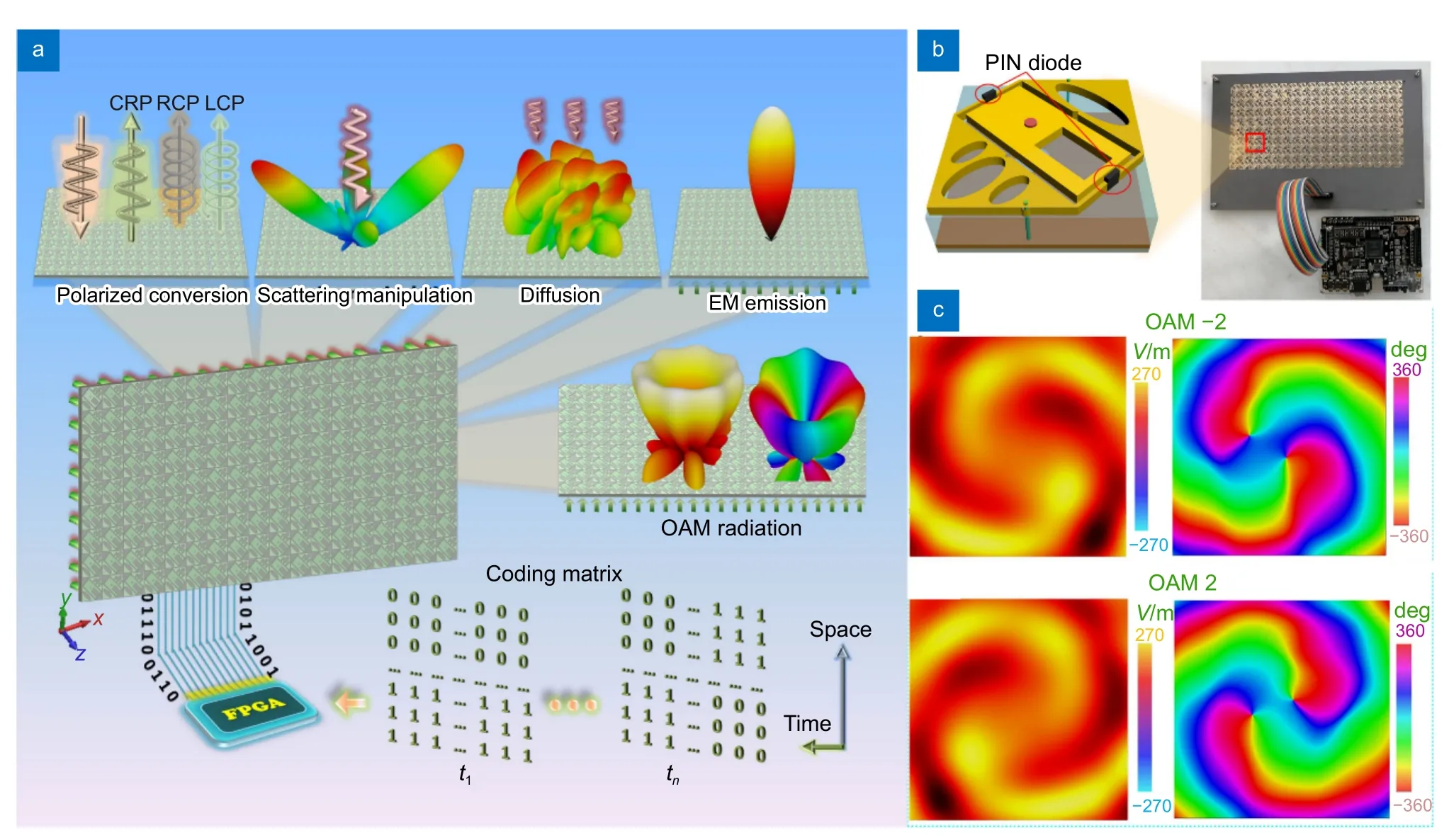
图10 一种可编程控制散射超表面[128]。(a) FPGA 控制超表面编码实现多功能转换；(b)超表面单元结构示意图与超表面实物图；(c)可编程超表面实现不同拓扑荷OAM 光束切换，光强及相位分布示意图Fig.10 A programmable controlled scattering metasurface[128].(a) FPGA controls the meta-surface coding to achieve multi-functional transformations;(b) Schematic diagram and physical picture of the metasurface unit structure;(c) Programmable metasurface achieves different topological charges of OAM beam switching,and the schematic diagram of the intensity and phase distribution

超表面单元的设计与无源金属超表面相比，主要是整合了PIN 二极管的控制电路。在单元顶层进行金属各向异性结构和发射贴片巧妙合理的布置，中心有槽的矩形旋转贴片可以反射电磁波。反射贴片周围的分裂环谐振器被设计为各向异性结构，用于控制反射EM 波的偏振。PIN 二极管连接图10(b)中的开口环谐振器，中间层上的铜是一个金属接地，端口连接发射贴片和金属接地，底部铜和下部基板构成控制电路。单元被预设为等效四分之一波片功能，通过二极管开关形成相位差以在y偏振光入射情况下生成拓扑荷分别为+2 和-2 模式的OAM 光束，如图10(c)所示，在近场中的模拟结果证明生成效果理想，可以清楚地观察到空间相位分布。类似地，还有2020 年Liu 等人提出的频域与空域可重构超表面[129]，以及2022 年Liu 等人提出的宽带可重构超表面[130]等，都是利用类似的设计原理，以“0”、“1”编码实现涡旋光束的生成。

对于光束状态复杂的矢量光束，仅仅通过两位编码还是略有不足，2020 年Shuang 等人在此基础上通过增加二极管的数量和电路排布方式[127]，增加每个单元的相位响应，使得单元数能够找到对应于00、01、10 和11 的四个编码状态，增加相位覆盖的密集度，当用相应的控制编码序列写入时，2 位可编程超表面可以用于生成具有高达6 个电子控制拓扑电荷和可控任意涡流中心的OAM 光束。同时，通过使用超表面卷积加法定理来为可编程超表面在OAM 无线通信中调制更加有趣的应用，如偏转和多模OAM 波束动态生成并独立控制。

构成超表面的单元结构如图11(a)所示，单个单元集成三个串联PIN 二极管，所有二极管具有由偏置电压(3.3 V 或0 V)控制的ON 和OFF 两种操作状态。当PIN 二极管工作在ON 状态时，它可以等效为寄生电感和电阻的串联电路；如果PIN 二极管处于OFF状态，则使用寄生电感、电容和电阻的串联电路来描述单元的物理等效模型。当通过FPGA 用不同的编码模式对超表面进行编程时，可以生成以原点为中心的单模OAM 光束，携带具有l=2、4、6 的不同拓扑电荷的光束，如图11(b)所示。无论是相位、光强还是OAM 谱的纯净度都要比1 bit 时得到了提升。当用相应的控制编码序列重新配置超表面时，可以操纵带有拓扑电荷l=1、2、3 的OAM 光束，并使其转向θ=±20°、0° 和 ±40°，如图11(c)所示，从以上结果中我们可以看出设计的超表面可以用于动态控制单模OAM 携带光束的拓扑电荷和涡旋中心。在此基础上，利用卷积加法原理进行编码也可以用于动态生成和控制多模OAM 携带波束，即生成的OAM 光束具有多个涡流中心或拓扑电荷，并且这些模式可以独立控制，如图11(d)所示，在同一平面上生成多个不同拓扑荷的OAM 光束，涡流数可以自由地控制。

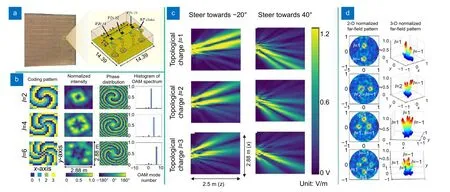
图11 一种2-bit 可编码超表面[127]。(a)超表面阵列实物与单元构成示意图；(b)利用超表面实现单模不同拓扑荷OAM 光束，包含超表面相位分布与仿真结果；(c)改变编码实现单模OAM 波束偏转不同角度光强示意图；(d)多模OAM 光束的生成与集成，包含近场与远场光强分布示意图Fig.11 A 2-bit encoded metasurface[127].(a) Schematic diagram of the metasurface array and unit composition;(b) Using the metasurface to realize a single-mode OAM beam with different topological charges,including the metasurface phase distribution and simulation results;(c) Changing the code to achieve different angles of deflection for a single-mode OAM beam,as shown by the schematic diagram of the light intensity;(d) The generation and integration of multi-mode OAM beams,including the near-field and far-field light intensity distributions

除了利用PIN 二极管偏压进行控制，超表面的可重构性也可以通过其他方式体现，如2020 年Zhang等人提出的利用光敏二极管替代传统PIN 二极管实现光驱动可重构超表面的方法，它可以通过光学编程来实现电磁功能[131]。该超表面有6 × 6 个子阵列，每个子阵列包含4 × 4 个基于变容二极管的超表面元件与基于光电二极管的光学电路集成。具体实现原理为将可见光照明模式转换为电压，并向超表面元件施加偏压，从而产生特定的微波反射相位分布。这种光学驱动的数字超表面可以实现隐身和动态涡流束生成。通过改变照明强度，每个超表面可以在较宽的频率范围(37.5%的相对带宽)内实现精确的180°相位差。在无线接收到不同的光模式后，超表面可以在其孔径上生成相位模式以实现不同的功能，如图12 所示。2022 年Chen 等人还提出了一种通过调节石墨烯费米能级来实现不同频段涡流束生成的可调谐超表面，在宽带可调谐范围内生成涡旋光，只是利用对石墨烯材料的调控进行调谐，不使用外加偏置电压的方式[132]。

图12 利用光敏二极管可调谐超表面实现不同功能[131]Fig.12 Using a tunable metasurface with a photodetector to achieve various functions[131]

智能超表面的出现使得超表面在矢量光束的生成方面更加灵活，额外地提供了时空调节的特性，尽管在相位上还不能达到无源超表面的精确覆盖，但是同样为这方面的研究提供了更多的可能，为下一代无线通信系统构建具有自主自适应可编程功能的智能超表面设备打下了坚实的基础。

5 总结与展望

矢量光场因其独特的特性一直是光学研究领域的热门，对矢量光束及其偏振态的研究无论是在经典光学还是量子光学中都非常重要，光子的自旋性为其研究赋予了更多可能。传统生成矢量光束的方式往往需要复杂的光路设计与繁多的装置，大大增加了研究成本。随着超表面的应用，利用微纳光学创造更加轻薄的器件，以集成光学系统替换传统光学系统生成矢量光，为这方面的研究提供了更多的可能性。例如设计可替代传统光学元件的超表面、利用高片上集成度实现复杂光场的单片生成、提高矢量光束生成效率等，结合时下热门的新材料，超表面能够不断焕发新的活力。

本文中提及的各种材料超表面均体现出了灵活性、高效性和紧凑性。超表面可以通过设计其微结构来实现对矢量光场的精确控制。可以通过调整超表面的结构参数来实现特定的光学功能，如相位调制、偏振控制等，从而灵活生成所需的矢量光场。同时，针对不同设计需求对材料进行选择，超表面可以实现高效的光场转换和调控。相比传统的光学元件，超表面具有更高的能量转换效率，减少了能量损耗，提高了光场生成的效率。最后，超表面可以实现光学功能的微型化和集成化。由于超表面的微结构可以制备在微米尺寸的平面上，因此可以将多个光学功能集成在一个超表面上，实现紧凑的矢量光场生成系统。

但是目前对于超表面生成矢量光的研究仍然存在一些挑战。首先是波长的限制，超表面的性能通常与入射光波的波长密切相关。超表面的设计和优化需要考虑光波的波长范围，因此在不同波长范围内的光场生成可能需要不同的超表面设计。其次是灵敏性，超表面对于入射光的角度和偏振状态较为敏感。微小的入射角度或偏振偏离设计值可能会导致超表面的性能下降，影响矢量光场生成的精确度和稳定性，以及制备的复杂性，超表面的制备和加工相对复杂，需要高精度的纳米加工技术和材料工艺。这可能导致超表面的制备成本较高，并对大规模生产造成一定的挑战。

现有的研究更多集中在功能的集成而非效率的提升上，在未来的研究中，可以考虑使用其他复合材料或新材料来提高传输效率，并且针对不同的使用场景对材料进行优化，可以提高超表面的普适性。以高传输效率的超表面进行级联可以赋予超表面更多的功能，这对于替换现有传统光路意义重大。同时利用新型的制造技术，如3D 打印技术也可以为超表面的制备注入新的力量，制造技术的进步会带动研究的发展。目前，可调谐超表面的研究也为动态调控超表面功能提供了新的思路，不同的调谐方式，如温控、电控等设计可以在空间变化的基础上引入时间的变化，时变相位可以使矢量光场的研究更进一步，如时空涡旋光的生成等。因此，利用超表面进行复杂矢量光束的研究仍然有深入探索的空间。