基于AK-SDMCS 的含缺陷核管道可靠性分析

薛国峰，汪大洋，张永山，苏迈佳

1. 佛山科学技术学院 交通与土木建筑学院，广东 佛山 528225

2. 广州大学 土木工程学院，广东 广州 510006

3. 特伦托大学 土木、环境与机械工程学院，意大利 特伦托 38100

管道系统是核电站冷却剂压力边界的重要组成部分，是核电站安全和正常运行的重要保障[1-3]。由于制造工艺及焊接等因素影响，管道系统不可避免地存在初始缺陷[4-5]。在运行荷载及温度、疲劳、腐蚀、老化等因素作用下，管道中可能萌生新的缺陷，已存在的初始缺陷则可能进一步扩展，直至发生泄漏、管道断裂等事故[6]。因此，非常有必要开展核电站含缺陷管道的安全评定[7]。

现行规范主要采用确定性方法进行管道安全评定。如英国R6 评定方法将含缺陷管道分为脆性断裂、塑性失稳和弹塑性断裂共3 种失效模式，根据管道及缺陷的几何尺寸、材料、荷载等因素判断失效模式，进而进行安全评定[8-9]。美国机械工程师学会（ American Society of Mechanical Engineers, ASME）管道与压力容器规范中的评定方法以R6 为基础，分别给出基于失效模式判定的含缺陷铁素体和奥氏体管道安全评定方法以及基于失效评定图的含缺陷管道安全评定方法[10]。但应注意到，管道系统的材料、几何形状、构造、工作环境及承受的荷载等均具有很强的随机性，缺陷形状、尺寸、位置和检测手段等也具有一定的随机性。在这些复杂因素综合作用下，核电站管道系统的工作状态及失效均表现出较强的随机性。因此，有必要采用概率统计方法合理考虑这些随机性，准确计算含缺陷管道的失效概率，从而准确评价管道的安全性和可靠性，为管道系统设计、优化、检测及维护提供理论基础[11-12]。

现有的含缺陷核管道可靠性分析方法主要包括一次可靠性方法(first order reliability method,FORM)、二次可靠性方法(second order reliability method, SORM)、 蒙特卡罗模拟(Monte Carlo simulation, MCS)及重要抽样法(importance sampling,IS)等[9,13-20]。FORM 和SORM 计算效率高，但对非线性功能函数计算误差较大[21]。数值模拟法(MCS、IS 等)计算精度高，但由于需要生成大量模拟样本并计算结构响应而计算量过大[22-23]。近年来，主动学习Kriging 代理模型可靠性分析方法由于同时结合了代理模型法效率高和数值模拟法精度高的优点而受到较多关注[24-27]。其基本思想是基于数值模拟法的样本池，采用主动学习方法以少量样本来训练代理模型，进而采用此代理模型代替真实结构功能函数来计算失效概率，从而实现了以少量结构功能函数调用（即少量结构分析次数）获得高精度失效概率的目的，提高了可靠性分析的计算效率和精度。经典的主动学习方法主要为基于主动学习 Kriging 代理模型的Monte Carlo 模拟方法(an active learning reliability method combining Kriging and Monte Carlo Simulation, AK-MCS)[25]，其主要基于MCS 样本池展开。但由于MCS 样本池容量通常很大，在其上进行主动学习时需要多次调用Kriging 模型计算响应。尤其是对于小失效概率问题，主动学习本身所需的计算量就非常大，阻碍了主动学习方法的应用。为了降低主动学习所需的计算量，人们提出基于方差缩减技术的主动学习可靠性分析方法如基于主动学习 Kriging 代理模型的重要抽样法 (a combined Importance sampling and active Kriging reliability method, AK-IS)和基于主动学习Kriging 代理模型的子集模拟方法(an active learning method combining Kriging and subset simulation, AK-SS)等[28-30]。但这些方法仍存在一些共性问题，主要包括：1)无法保持AK-MCS 的通用性；2)需要前处理获取失效域信息；3)抽样区域大于重要区域，使得在对失效概率无较大贡献的区域内浪费了部分功能函数调用。因此，本文提出了基于参数空间球分解蒙特卡罗模拟的主动学习代理模型可靠性分析方法（an active learning reliability method combining adaptive Kriging and spherical decomposition-MCS, AK-SDMCS）[31]，其通过将参数空间沿着径向由内向外划分为一系列超球环，从而将整个空间内进行的主动学习分解为一系列超球环内的主动学习，通过“化整为零、分而治之”，提高了主动学习的计算效率。AKSDMCS 既保持了AK-MCS 的通用性和鲁棒性，同时克服了在求解小失效概率问题时主动学习本身计算量过大的困难。

因此，本文围绕含缺陷核管道可靠性分析开展研究。首先，基于ASME 锅炉与压力容器规范建立含环向内表面缺陷核管道的可靠性分析模型，包括塑性失稳、弹塑性撕裂失稳和脆性断裂3 种主要失效模式及对应的极限状态方程，归纳凝练了含缺陷核管道可靠性分析应考虑的随机因素：运行压力、缺陷尺寸、材料断裂韧性和流变应力等；其次，基于参数空间径向球分解思想，将整个参数空间内生成的样本池上进行的主动学习（AK-MCS）分解为划分所得的一系列超球环内样本池上的主动学习，降低主动学习的计算量，克服AK-MCS 对小失效概率计算量过大的缺点，建立AK-SDMCS 方法；最后，采用AK-SDMCS 计算含缺陷核管道的失效概率，建立高效适用的含缺陷核管道可靠性分析方法。本文还给出3 个不同数量级（10-5~10-3）的算例，通过与MCS、AKMCS 对比，验证了所提AK-SDMCS 进行含缺陷核管道可靠性分析的计算精度和效率。

1 含缺陷核管道可靠性分析模型

1.1 含缺陷管道截面参数

本文主要研究含环向内表面缺陷核管道的可靠性分析，截面如图1 所示。

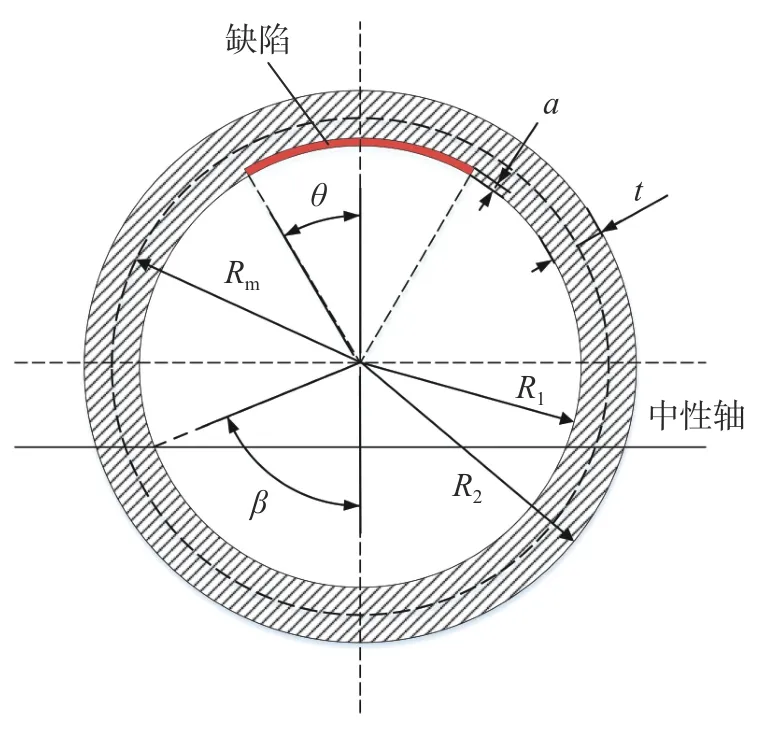
图1 含缺陷核管道截面示意

图1 中t为管道壁厚，mm；R1、R2、Rm分别为管道内半径、外半径和平均半径，mm；缺陷通常简化为弧形，a为 缺陷深度，mm； θ为缺陷半长度角(弧度制)；c=θ·R1为缺陷半长，mm；l=2c为缺陷长度，mm； β为中性角(弧度制)。

1.2 含缺陷核管道失效模式

含缺陷管道的失效模式通常分为塑性失稳、弹塑性撕裂失稳和脆性断裂3 类，主要通过综合考虑了荷载、缺陷尺寸、材料性质等因素的筛选参数SC进行判别[32]，如图2 所示。

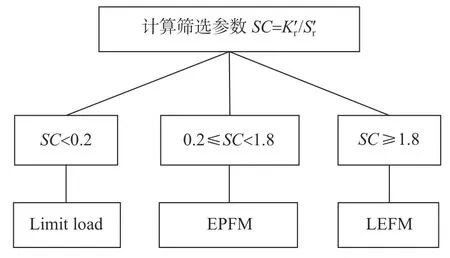
图2 判断含缺陷核管道的失效模式

1) 当SC< 0.2 时，判定为塑性失稳失效模式，需要进行极限塑性荷载分析(limit load (fully plastic) analysis)。

2) 当0.2≤SC<1.8 时，判定为弹塑性撕裂失稳失效模式，需要进行弹塑性断裂力学分析(elasticplastic fracture mechanics analysis, EPFM)。

3) 当SC≥1.8 时，判定为脆性断裂失效模式，应采用线弹性断裂力学方法分析(linear elastic fracture mechanics analysis, LEFM)，一般以应力强度因子为判据。

筛选参数SC按下式计算：

应力强度因子KI为

式中Fm和Fb为计算参数，可参考ASME 规范计算，二者均为管道内径和缺陷尺寸的函数；Q为缺陷形状无量纲参数。

式中： σy为材料屈服强度； σf为材料流变应力，一般定义为屈服强度和拉伸强度的平均值。中性角β计算为

其中

塑性失稳时的极限状态方程（对应SC< 0.2）为

式中SC1为塑性失稳条件下的许用弯曲应力。

式中：SFb和SFm为结构系数，一般根据管道所处的不同工况取不同值；为失效弯曲应力。

塑性失稳时的极限状态方程（对应0.2 ≤SC<1.8）为

式中SC2为塑性失稳条件下的许用弯曲应力。

式中Z是根据管道尺寸计算得到的乘子，可参考ASME 规范计算。

脆性断裂失效时的极限状态方程（对应SC≥1.8）为

式中Kc=(JIcE′/1 000)0.5为材料的临界断裂韧性。应注意的是，这里的应力强度因子计算公式不同于计算SC时采用的应力强度因子，主要区别在于取消了缺陷形状无量纲参数Q，并增加了结构系数SFb和SFm。应力强度因子具体计算公式为

其中

式中Fm和Fb的计算公式同前文，均可参考ASME 规范计算。

1.3 随机参数

含缺陷核管道可靠性分析考虑的随机因素主要为运行压力、缺陷尺寸、材料断裂韧性和流变应力等[13]。

1.3.1 运行压力的随机性

管道所受的流体内压p通常假定为正态分布随机变量。根据内压计算薄膜应力 σm和弯曲应力σb，通过对数据统计则可获得相应的概率分布。应注意到 σm和 σb均依赖于内压p，显然二者并非相互独立随机变量。实际处理中，可通过有限元分析等手段建立内压与薄膜应力和弯曲应力的确定性函数关系，如σm=f(p)和σb=h(p)，进而由内压的概率分布推导出薄膜应力和弯曲应力的概率分布。在随机模拟场合，只需生成内压的随机样本，再把这些随机样本代入确定性函数f(p)和h(p)，则可获得对应的薄膜应力和弯曲应力样本[15]。

1.3.2 缺陷尺寸的随机性

为了便于计算，环向内表面缺陷通常简化为弧形。由检测精度和表征误差引起的缺陷深度和长度的随机特征一般均可表示为正态分布，相关分布参数可通过对大量实测数据统计获得[33-34]。

1.3.3 流变应力和断裂韧性的随机性

由于制造工艺、检测手段等多种复杂因素影响，材料性质通常并非常数。即使是同一批次生产，材料性质仍表现出较大的随机性。对于含缺陷核管道可靠性分析，材料的流变应力和断裂韧性为主要影响参数，对应的概率分布可通过对实测数据统计分析获得，通常假定为对数正态分布[33]。

1.4 含缺陷管道的极限状态函数

综上，含环向内表面缺陷核管道的极限状态函数可表示为三分段函数，如下式所示：

式中x为基本随机变量，这里主要包括薄膜应力σm、弯曲应力 σb、缺陷深度a、缺陷长度c(或缺陷半长度角θ)、流变应力 σf和断裂韧性JIC等。基于上述极限状态函数，含缺陷管道的失效概率可表示为

式中fX(x)为基本随机变量的联合概率密度。

2 含缺陷核管道可靠性分析方法

2.1 Kriging 模型

Kriging 模型由Krige 和Matheron 等首先提出并应用于地质统计学[35]，后应用于计算机模拟试验[36]、全局优化[37]等领域。在结构可靠性分析领域，Kriging 模型主要用作一种代理模型[38-39]。此外，很多主动学习可靠性分析方法均基于Kriging 模型建立[24,40-41]。

Kriging 模型为基于统计理论的半参数插值模型，由参数化的线性回归模型和非参数化的随机过程2 部分组成[37]。线性回归模型表示原函数的整体趋势，随机过程则用于修正回归模型的偏差。Kriging 模型的应用主要包括2 步：首先基于给定的实验设计确定模型参数；其次通过最佳线性无偏预测计算结构在新输入样本下的响应。给定实验设计：

式中：fT(x)β和f(x)=[f1(x),f2(x),···,fm(x)]T分别为回归模型和基函数；β=[β1,β2,···,βm]T为对应的回归系数。本文采用常数回归模型，即取f(x)=1，β=β，从而将Kriging 模型简化为

式中z(x)为零均值平稳高斯过程，其协方差为

式中： σ2为随机过程的方差；R(x,w)为任意两点x和w的自相关函数，通常采用高斯自相关函数。

式中：xi和wi分别为点x和w的第i个分量， θi为第i维的相关参数。

令R为p×p维对称相关矩阵， 其中Rij=R(x(i),x(j)),i,j=1,2,···,p，F为p×1维单位向量，则回归系数 β和随机过程的方差 σ2可按以下式进行估计：

相关参数 θ可采用极大似然法按下式估计：

对于新输入样本x(0)，Kriging 模型可给出结构响应的最佳线性无偏预测和相应的Kriging方差，分别为

式中

容易验证，对实验设计中每一个样本x(i)，均有即Kriging 模型为精确插值模型。对于实验设计之外的输入样本，Kriging 方差一般不为0，可表示模型预测值的局部不确定性。因此，Kriging 方差常被用于改进实验设计和提高代理模型精度。本文采用MATLAB工具箱DACE 进行Kriging 模型的构造与预测[42]。

2.2 AK-SDMCS 简介

AK-SDMCS 的基本思想是首先将参数空间沿着径向由内向外划分为一系列超球环（即参数空间球分解）；其次，在这些超球环内分别采用主动学习方法构造Kriging 模型；最后，采用最终获得的Kriging 模型计算结构响应和失效概率。

2.2.1 SDMCS

首先，将参数空间D=沿径向划分为一系列互不重叠且完备的子区域Di,i=1,2,···,m，使得：

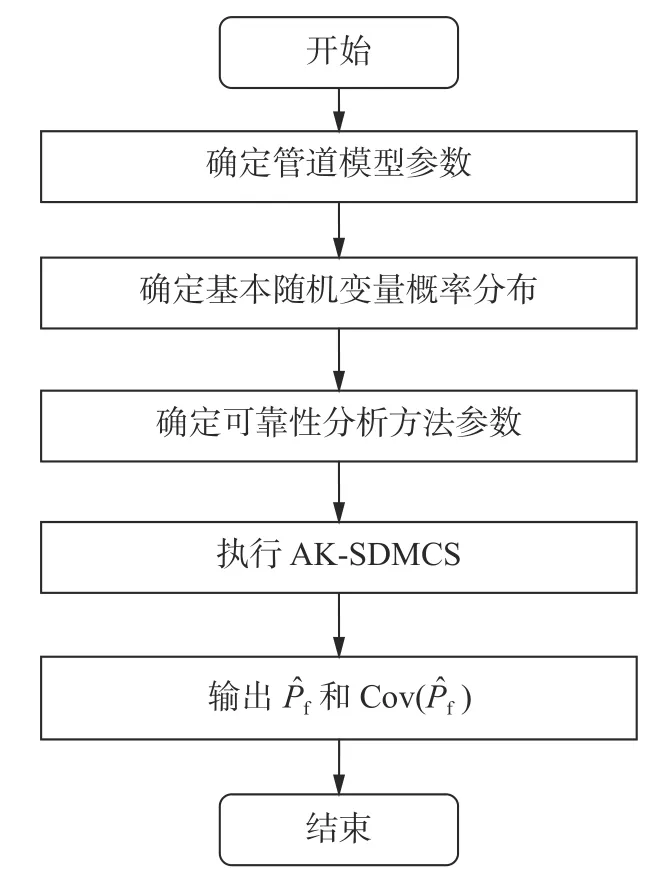
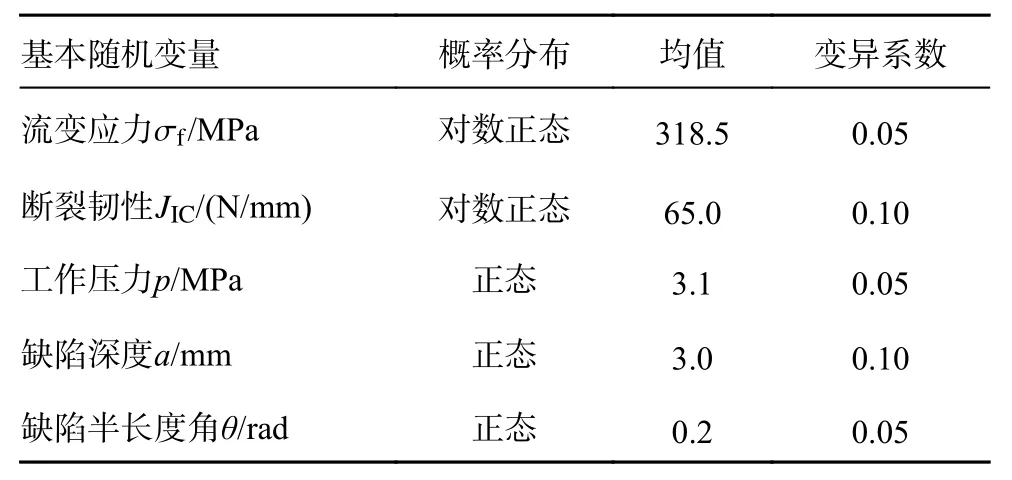
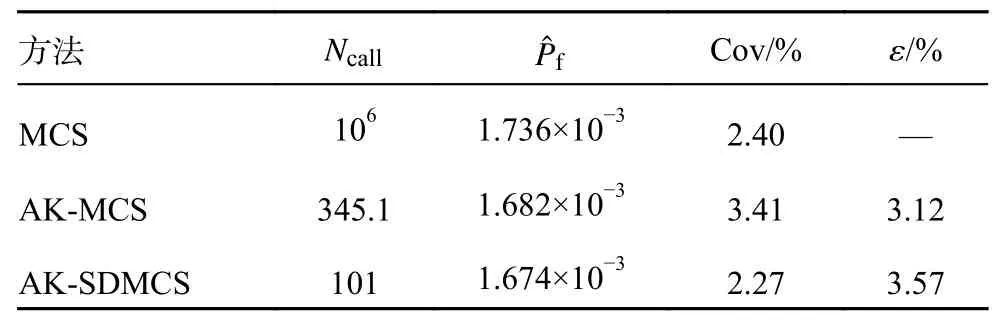
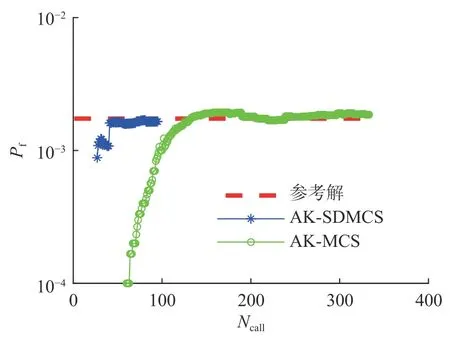
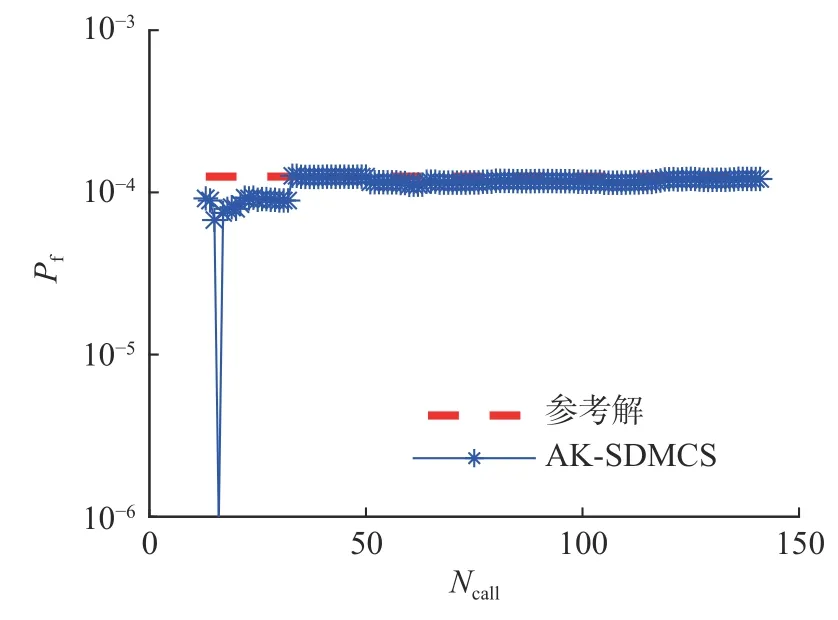
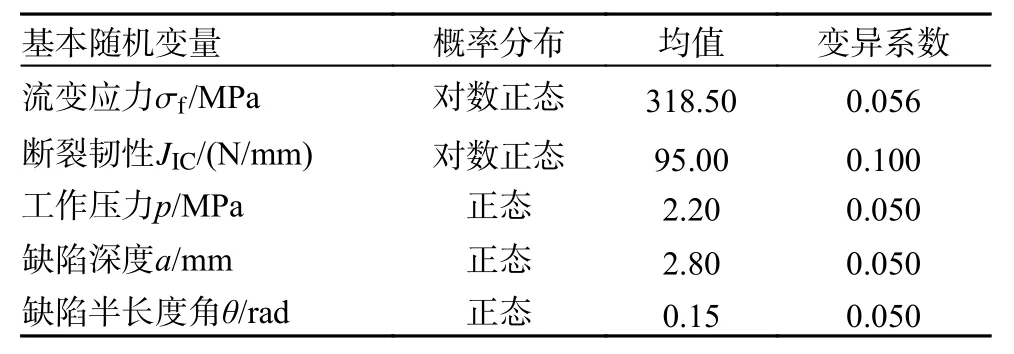
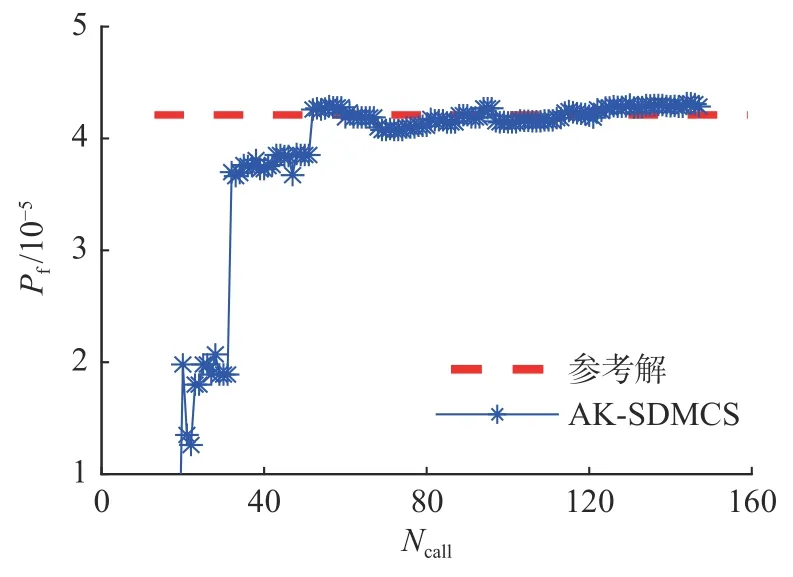
式中：Di={x|Ri-1≤∥x∥

定义子区域Di上的截断概率密度为

将式(5)代入式(4)可得失效概率估计：

对应的估计方差为

参数空间的球分解也采用自适应方式进行。首先将空间沿着径向划分为2 个超球环，然后将外侧超球环进一步划分为2 个超球环，如此重复迭代直到最外侧超球环中所需的样本量小于事先规定的样本量，即可自动确定半径序列R0

由于标准正态空间内样本到原点的距离服从自由度为N的卡方分布(|x|2)， 因此有=(1-10-j)。当最外侧超球环(子区域)内所需的样本量满足≤∆N0时，表明个样本即可充分探索该区域（注：=NMCSθi，NMCS可由事先设定的变异系数，结合MCS 计算公式获得。实际应用中，失效概率通常未知，可采用当前失效概率估计值替代）。此时，可停止空间分解，相应的超球环数量即为m。

2.2.2 AK-SDMCS

在SDMCS 基础上，在每个超球环内分别采用主动学习方法构造Kriging 代理模型，并采用最终获得的Kriging 模型计算失效概率，即可建立AK-SDMCS。

AK-SDMCS 的初始实验设计采用拉丁超立方抽样(latin hypercube sampling, LHS)生成。模拟区域选为[u±VMσ]，其中u和 σ分别为基本随机变量的均值和标准差，VM为标准差缩放系数。初始实验设计的样本容量为max{15,N+2}。由于LHS 具有更好的空间填充特性，因此，训练所得的初始Kriging 模型将较好地刻画真实功能函数的全局特征。

其次，考虑到经典的AK-MCS 采用的停止条件过于保守[43]，本文提出由AK-MCS 的停止条件和文献[44]中的停止条件组成的复合停止条件。

其中第1 个停止条件表示失效域的稳定性。

式中为第j轮主动学习迭代中的失效样本数量。第2 个停止条件表示相邻2 次主动学习中候选样本响应符号发生变化的比例。

式中：NS为候选样本总量；为第j轮迭代训练所得的代理模型； ×表示异或运算；ε1,ε2为2 个阈值，均取0.001[44]。

2.3 基于AK-SDMCS 的含缺陷核管道可靠性分析方法

基于前文建立的含缺陷核管道可靠性分析模型，根据基本随机变量概率分布生成样本，采用AK-SDMCS 计算失效概率，即可建立基于AKSDMCS 的含缺陷核管道可靠性分析方法，基本流程如图3 所示。

图3 含缺陷核管道可靠性分析基本流程

方法基本步骤如下：

1) 初始化：主要包括确定管道参数和基本随机变量的概率分布以及AK-SDMCS 基本参数：Kriging 模型的超参数、初始实验设计抽样区域和容量N0、失效概率估计的目标变异系数 δ0、子区域内的初始样本池容量∆N0、主动学习停止条件的2 个阈值ε1和ε2，参数空间球分解的半径序列为

2) 空间球分解和子区域Dm-1内抽样：将外层超球环划分为2 个子区域。令m=m+1，在次外层超球环Dm-1内生成∆N0个样本。

4) 空间球分解的停止条件：计算最外侧超球环所需的样本量=NMCSθi。若>∆N0，则返回步骤2)；反之，若≤∆N0，则继续执行步骤5)。

5) 生成最外侧超球环Dm内的个样本。

3 算例分析

本节通过3 个算例验证所提方法的有效性、计算精度和效率。3 个算例具有不同数量级的失效概率，用于考察可靠性分析方法对失效概率量级的鲁棒性。AK-SDMCS 的计算参数取值如下：目标变异系数取为δ0=5%；Kriging 模型超参数初值取100，搜索范围取[10-3, 103]；子区域内初始样本量和后续样本增量均为∆N0=104；初始LHS 抽样区域为[µ±6σ]；初始实验设计容量取N0=12；主动学习停止条件的2 个阈值取ε1=ε2=0.001。作为对比，分别采用MCS 和AK-MCS 对这3 个算例进行可靠性分析。失效概率估计的目标变异系数均取 5%。AK-MCS 的计算参数为：初始实验设计容量取50，采用随机抽样方式在区域[µ±6σ]内生成；Kriging 模型超参数初值取10，搜索范围取[0.1, 20]。

对所有算例均采用MCS 计算结果作为参考解。AK-MCS 和AK-SDMCS 均独立运行10 次，以获取平均结果和经验变异系数。通过比较所需的功能函数调用次数Ncall、失效概率变异系数和相对误差来验证所提方法的精度和效率。

3.1 算例1 (10-3 量级)

管道模型参数如表1 所示。假定管道处于正常工况，结构系数分别取SFb=2.3和SFm=2.7。材料的流变应力 σf和断裂韧性JIC、工作压力p、管道内壁环向表面缺陷的深度a和半长度角θ均假定为随机变量，对应的概率分布参数如表2 所示。为便于验证，这里参考文献[14]将含缺陷截面处的薄膜应力和弯曲应力分别取为σm=9.625p+3.2，σb=18.38p+10.83。

表1 算例1 管道模型参数

表2 算例1 基本随机变量分布参数

分别采用MCS、AK-MCS 和AK-SDMCS 计算该管道的失效概率，结果如表3 所示。可以发现，AK-MCS 和AK-SDMCS 均具有较低的变异系数（最大约3.41%）和相对误差（最大约3.57%），所得的失效概率估计具有较高的精度。而在结构功能函数调用次数方面，二者均比MCS 减少了4 个数量级，验证了主动学习可靠性分析方法较高的计算效率。和AK-MCS 相比，AK-SDMCS 仅需29.3%（不到1/3）的结构功能函数调用次数，即可获得相近精度的失效概率估计，计算效率更高。

表3 算例1 可靠性分析结果

图4 为本文方法在一次典型计算中的失效概率收敛曲线，其中红色虚线为MCS 所得的失效概率参考值。AK-MCS 在迭代约130 次后接近参考值，共调用结构功能函数333 次；而AK-SDMCS则在迭代约40 次后就接近失效概率参考值，所需的结构功能函数调用次数仅为95，收敛速度更快，计算效率更高。

图4 算例1 失效概率收敛曲线

此外，10 次独立运行中，AK-MCS 和AKSDMCS 的样本池容量均值分别为2.43×105和70 440。可以看出，AK-SDMCS 显著减少了样本池容量（为AK-MCS 的29.0%）。由于主动学习过程需要基于样本池中的样本重复进行Kriging 模型训练和预测，故AK-SDMCS 也降低了代理模型主动学习的计算量。通过减少样本池容量、参数空间划分以及降低结构功能函数调用次数，AKSDMCS 进一步提高了可靠性分析的计算效率。

3.2 算例2 (10-4 量级)[14]

管道模型参数如表4 所示。结构系数同算例1，分别取SFb=2.3和SFm=2.7。基本随机变量的概率分布参数如表5 所示。假定含缺陷截面处的薄膜应力和弯曲应力分别为σm=10.66p+5.3，σb=18.25p+7.64。

本算例中，AK-SDMCS 方法10 次独立运行生成的样本池容量均值为1.97×105。而AK-MCS 则需要生成容量为3.2×106的样本池（按5%变异系数估算）。这时，Kriging 代理模型本身的训练和预测就需要大量的计算资源，个人电脑（CPU：Intel Core i7-10510U；内存：32 GB；硬盘：250 GB固态）已无法进行计算。其根本原因在于，主动学习的每一轮迭代都需要基于当前实验设计点更新Kriging 模型，并采用更新后的Kriging 计算样本池内所有样本的响应值和方差。这导致主动学习本身就需要大量计算资源，使得AK-MCS 无法进行，故表6 仅列出MCS 和AK-SDMCS 的计算结果。可以看出，AK-SDMCS 所得的失效概率估计变异系数与MCS 接近，相对误差为3.96%，具有较高的计算精度。在计算量方面，AK-SDMCS所需的功能函数调用次数比MCS 减少了5 个数量级，显著提高了可靠性分析的计算效率。图5为AK-SDMCS 在一次典型计算中的失效概率收敛曲线。

表6 算例2 可靠性分析结果

图5 算例2 失效概率收敛曲线

3.3 算例3 (10-5 量级)[15-16]

本算例管道模型的外径377 mm、壁厚10 mm，其余确定性参数均与算例1 相同。基本随机变量的概率分布参数如表7 所示。假定含缺陷截面处的薄膜应力和弯曲应力分别为σm=9.625p+5.4 , σb=25.24p+4.7。

表7 算例3 基本随机变量分布参数

表8 列出了可靠性分析结果。10 次独立运行中， AK-SDMCS 的样本池容量均值为3.62×105。类似于算例2，AK-MCS 由于样本池容量太大而无法进行，再次验证了AK-MCS 不适用于小失效概率问题。本文所提AK-SDMCS 给出的失效概率估计变异系数与MCS 接近，相对误差仅为0.62%，所需的结构功能函数调用次数仅为158.3，比MCS 减少了5 个数量级，计算效率有了明显提高。图6 为AK-SDMCS 在一次典型计算中的失效概率收敛曲线。

表8 算例3 可靠性分析结果

图6 算例3 失效概率收敛曲线

比较3 个算例可以发现， AK-SDMCS 对10-5~10-3数量级范围的失效概率均具有较高的计算效率，所需的结构功能函数调用次数为101.0~158.3，并没有随失效概率量级的增加而大幅增加。表明AK-SDMCS 方法对失效概率量级不敏感，具有较好的鲁棒性。

4 结论

本文基于ASME 锅炉与压力容器规范建立了含缺陷核管道的可靠性分析模型，包括失效模式、主要随机参数以及极限状态方程。进而，基于Kriging 代理模型及参数空间球分解思想，建立了适用于含缺陷管道可靠性分析的主动学习代理模型方法（AK-SDMCS），并通过3 个不同数量级的算例验证了所提方法的适用性、精度和效率。结果表明：

1) 所提方法只需少量功能函数调用次数即可给出高精度的失效概率估计（对10-5~10-3数量级范围的失效概率，所需功能函数调用次数在102量级），具有较高的精度和效率。

2) 与主动学习方法AK-MCS 相比，所提方法既保留了AK-MCS 通用性和鲁棒性的优点，同时通过空间球分解思想显著降低了主动学习的计算量（特别是对小失效概率问题），克服了AK-MCS求解小失效概率时计算量过大的缺点。

3) 所提方法对失效概率数量级具有一定的鲁棒性，所需的结构功能函数调用次数并未随着失效概率数量级的增加而显著提高。

4) 克服了现有方法面临的计算量大、精度低等缺点，可为含缺陷核管道可靠性分析提供高效适用的途径。