低气压条件下弓网滑动电接触粗糙表面特性研究*

2023-11-13王图南寇佳宝郭凤仪

机电工程技术 2023年10期

王图南，寇佳宝，郭凤仪

（温州大学电气与电子工程学院，浙江温州 325035）

0 引言

受电弓—接触网系统是电气化铁路的关键部件之一。高速列车运行过程中所需电能通过弓网稳定接触进行取流，真实接触斑点的数量决定了系统运行的可靠性。弓网系统在高速运行时受到滑动摩擦和接触电流的双重作用，从而引起滑板与接触线的接触区域温度大幅度升高。这种温升会改变滑板表面的真实接触状态，使真实接触面积发生变化，因此摩擦副表面加剧磨损[1]。引起接触区域温度升高的原因有很多，如弓网振动压力、滑动摩擦、接触电流、接触线暴露于低温潮湿环境[2]下、寒冻环境下覆冰[3]等。近年来，恶劣环境带来的列车安全运行问题层出不穷。由于弓网系统需要维持在一定温度范围内才能更好地保持电气性能，所以对特殊环境下弓网系统载流摩擦副表面温升特性进行研究具有重要意义[4]。

M Szulborski 等[5]通过建立高压断路器三维有限元耦合仿真模型，研究了接触系统在接触对上的电动力特性，得出电动力的值在2 kN 时接触点的严重变形会造成接触系统损坏的结论。F Guo 等[6]建立考虑粗糙面的滑动电接触温度场仿真模型，分析表面粗糙度和分形参数对接触面温度的影响，得出了随着分形维数增加或分形粗糙度减小，接触区域温度不断降低的结论。H Zhao 等[7]采用Fluent 流体仿真软件建立电弧侵蚀模型，分析直流28 V电源下发生电弧时电弧能量对飞机铝板结构的损伤机理，可用于预测电弧对物体的损伤程度。A Maharaj 等[8]建立氦等离子体的流体动力学模型，研究等离子体在高压和小电流条件下的放电演化过程，得出了鞘层模型和热力学性质对电势有显著影响的结论。Z Han 等[9]建立弓网电弧磁流体仿真模型，研究不同车速条件以及正面气流影响下弓网电弧的运动特性。J Deng[10]建立考虑流-固-电多物理场耦合的换流变压器内部的电弧放电仿真模型，计算故障能量为230 kJ 时内部压力和强度的变化特征，为减少换向器故障火灾提供了有效的数值模拟方法。Z Yang 等[11]建立受电弓电弧的磁流体动力学模型，通过考虑横向侧风和输入电流对电弧动力学行为进行了数值模拟计算，详细研究其对电弧温度和电弧电压的影响。周昱涵等[12]建立了二维磁流体动力学模型探究高海拔地区的弓网电弧运动特性，得出了采用更大半径的接触线或者减小接触线底部的曲率可以有效加快电弧运动，从而减轻电弧烧蚀的结论。

近年对弓网系统温升特性的研究主要集中在波动载荷、电弧侵蚀、受流质量以及摩擦磨损[13]等方面，对于恶劣气候环境如降雨、覆冰、峡谷风等的研究[14]较少。川藏铁路所在地区的环境气压比起国内其他地区显著降低。国内外关于低气压环境的主要研究聚焦于电弧的运动特性[15]，而对于整体弓网系统接触区域温度的研究很少。本文建立滑动电接触粗糙表面微观接触模型，结合运行速度和接触电流对接触面稳态温升的规律，计算并分析流-固多场耦合下不同气压与流速对弓网系统流场和压力的影响特性。为低气压条件下弓网滑动摩擦副建模优化以及降低极端环境对弓网系统的冲击提供了理论支持。

1 仿真模型与边界条件

1.1 三维粗糙表面形貌模拟

粗糙表面之间的接触是以接触斑点的形式存在的，实际的接触表面是粗糙且不连续的。本文将弓网接触问题等效为粗糙表面与光滑表面之间的接触问题，其中滑板表面为粗糙表面，接触线为刚性光滑表面。

本文采用了W-M函数来建立滑动电接触的粗糙表面接触模型[16]，分形方程如式（1）和式（2）所示。首先对实体滑板表面粗糙度数据进行采集，其次采用结构函数法[17]计算分形维数D和分形粗糙度G，最后根据式（1）所建立的粗糙表面三维模拟图如图1 所示。其中分形维数D代表粗糙表面轮廓的起伏程度，D越大则表明粗糙表面的轮廓越复杂。特征尺度参数G模拟粗糙表面形貌的高度，G越大表明表面粗糙峰值越高。

图1 三维分形粗糙表面帷幕

式中：L为取样长度，即视在接触面的边长，m；D为二维几何的分形维数，2＜D＜3；G为分形粗糙度，m；γ为尺度参数，γ＞1，通常取γ=1.5；M为用于构造随机形貌的不同方向的叠加脊数量，通常取M＞10；φmn为[0，2π]区间均匀分布的随机相位；nmax为最高频率分量阶数；int[·]为最高频率的最大整数；LS为截止频率。

1.2 几何模型构建

根据实验室自制的高性能滑动电接触实验机的实际尺寸对固体模型进行建模，建模流程如图2所示。图3所示为所建立的流-固耦合三维弓网系统模型图，图中圆环部分为铜接触线，其圆环半径为491 mm，截面半径为8 mm，磨损量为1 mm，运动方式设定为绕圆环圆心旋转。圆环左侧为浸金属碳材料的受电弓滑板，其形状为平行六面体，尺寸为250 mm×25 mm×10 mm，受电弓滑板沿长度方向进行往复运动。圆环右侧为铜材质的电刷，尺寸为200 mm×30 mm×10 mm。浸金属碳滑板的杨氏模量为1 260 MPa，泊松比为0.425，电导率为7 800 S∕m，导热系数为260 W∕（m·K），密度为2 400 kg∕m3，恒压热容为700 J∕（kg·K）。铜接触线的杨氏模量为110 000 MPa，泊松比为0.35，电导率为5.56×107S∕m，导热系数为380 W∕（m·K），密度为8 700 kg∕m3，恒压热容为380 J∕（kg·K）。接触部分的摩擦因数均为0.2，流体计算域尺寸为1 500 mm×1 200 mm×100 mm，材料为空气。

图2 固体模型建立流程

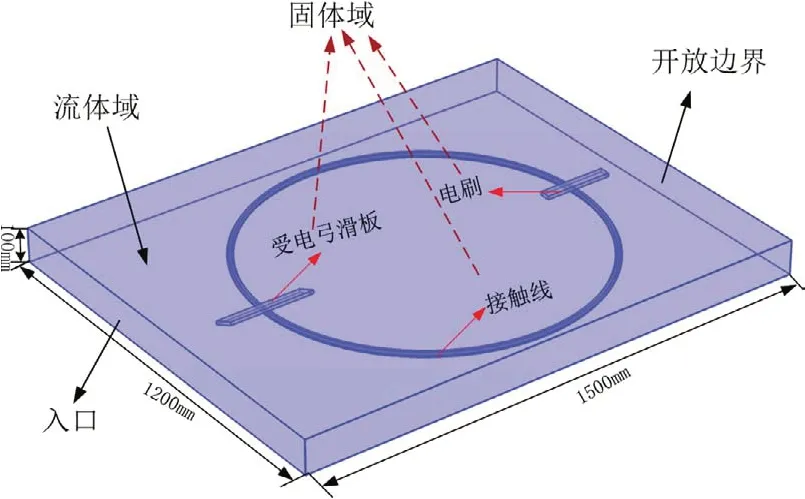
图3 三维流-固耦合弓网系统接触模型

1.3 网格剖分与基础假设

为了提高模型精度和收敛性，采用用户控制网格进行网格剖分，网格剖分图如图4 所示。普通物理学部分定义粗化网格，流体动力学部分定义为常规网格。根据空气流动属性，在流体与固体模型交界处采用边界层自动收缩狭窄区域。最后完整网格包含596 820 个域单元、39 312个边界单元和6 047个边单元。四面体网格单元有53 072 个，三角形单元有38 856 个，最小单元质量为0.02，平均单元质量为0.66，能够满足网格耦合计算要求。该模型的建立需满足如下假设：（1）假设材料表面各项同性；（2）考虑到接触区域温升的温度范围，忽略电弧热；（3）忽略表面对表面的辐射传热。

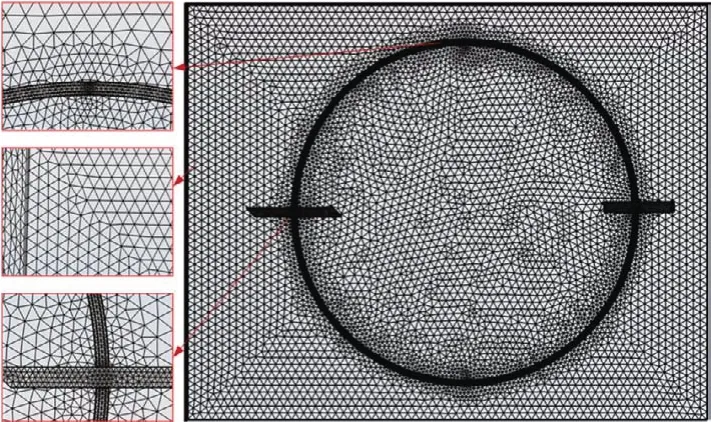
图4 网格剖分

1.4 流-固耦合控制方程

基于纳维-斯托克斯理论，守恒定律根据以下几个方程进行描述，其中质量守恒方程为：

动量守恒方程为：

能量守恒方程为：

式中：ρ为密度，kg∕m3，Cp为恒压热容，J∕（kg·K），T为绝对温度，K；u为速度矢量，m∕s；q为传导热通量，W∕m2；qr为辐射热通量，W∕m2；αp为热膨胀系数；τ为黏性应力张量，Pa；Q为除黏性耗散外的热源，W∕m3。

1.5 边界条件与参数设定

本文参考青藏高原所处空气热力学参数划分出6 个气压等级，分别为50、60、70、80、90 和101 kPa。流体域的外表面为热绝缘边界，图3 的流体计算域左侧定义为流体入口，设定充分发展的流动，给定初始平均速度为5 m∕s，右侧设定为开放边界，正应力为0。

2 低气压条件下弓网模型实验验证及粗糙表面特性仿真研究

2.1 标准大气压下弓网模型可行性验证

设置以下两种工况条件：（1）滑动速度为50 km∕h，接触电流为60 A，接触压力为60 N；（2）滑动速度为80 km∕h，接触电流为80 A，接触压力为60 N。初始环境温度为293.15 K，运行时间为100 s。在标准大气压条件下对弓网系统滑动电接触粗糙表面接触区域温度分别进行实验与仿真研究。图5 所示为自行研制的高性能滑动电接触实验机，实验结束后采用红外热像仪拍摄并捕捉接触区域最高温度，如图6（a）和图7（a）所示。在同样的工况条件下进行仿真，计算出接触区域最高温度结果如图6（b）和图7（b）所示。由图6 可知，第一种工况下实验与仿真得到的滑板表面温度的最大值分别为39.4、36.4 ℃，误差为3 ℃。由图7 可知，第二种工况下实验与仿真得到的滑板表面温度的最大值分别为46.1、45.2 ℃，误差为0.9 ℃。仿真模型与实验系统的接触区域温度高度吻合，可知仿真模型具有较高的精度和系统可行性。

图5 高性能滑动电接触实验系统

图6 I=60 A，F=60 N，v=50 km∕h工况下滑板表面瞬态温度

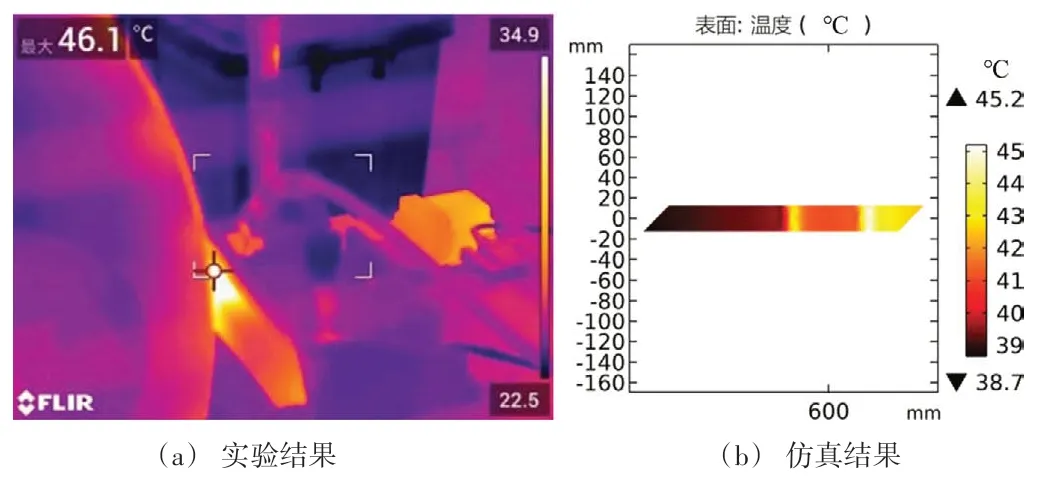
图7 I=80 A，F=60 N，v=80 km∕h工况下滑板表面瞬态温度

2.2 低气压条件对弓网接触区域稳态温升的影响

对不同气压下的滑动电接触粗糙表面接触区域的稳态温度进行仿真计算。设定如下仿真条件：滑动速度为400 km∕h，接触电流为500 A，接触压力为60 N，气压等级分别为50、60、70、80、90、101 kPa，仿真时间设定为600 s。根据仿真结果获得了不同气压对接触面稳态温度的影响规律，如图8 所示，气压越低，粗糙表面接触区域的稳态温度越高。随着气压降低，接触区域的温度时间常数增加。起初45 s 温度上升阶段，气压越低，温度增长速率越大。这是由于气压越低，空气密度越小，滑板表面散热越慢，进而导致滑板表面的温升越高。

为了研究低气压环境下滑动速度与接触电流对粗糙表面接触区域温度的影响，在滑动速度分别为200、400 km∕h，接触电流分别为400、700、1 000 A 的条件下进行仿真，仿真时间仍设定为600 s。如图9 所示，当接触电流一定时，随着气压从50 kPa增大到101 kPa，接触区域的稳态温度逐渐降低，并且气压越高，温度降低的速率越慢。低速条件下的稳态温度比高速下要高，这是由于高速运行时接触面的散热加快，其温度也更易达到稳态。此外，滑动速度对不同气压等级下的接触区域温度会存在不同程度的影响。在气压过低或更接近标准大气压时，速度对接触面温度的影响较小。而气压分在60、70、80 kPa 时，速度对接触面温度的影响更大。图10 所示为不同气压等级下接触电流对接触面稳态温度的影响。当滑动速度一定时，随着气压的升高，接触面温度不断下降，且低气压范围内温度下降更快。而气压一定时，不同的接触电流对接触面稳态温度的影响不大。

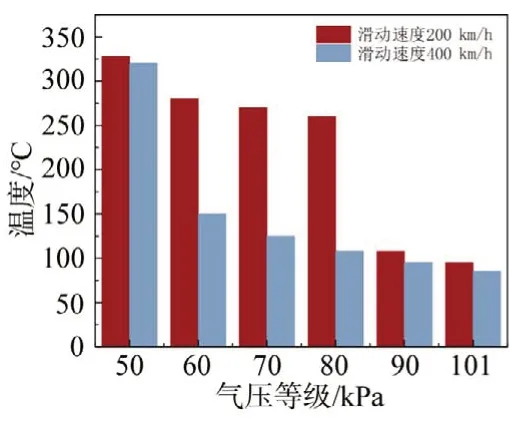
图9 不同速度下气压等级与接触区域稳态温升的关系

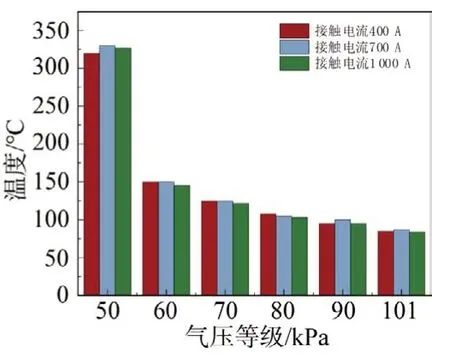
图10 不同电流下气压等级与接触区域稳态温升的关系

2.3 低气压条件下气体流速对弓网接触区域温度场及速度场的影响

为了研究不同气压条件下稳态温度对接触线周围流场分布的影响，基于表1 所示的参数对流体域进行仿真计算[18]。取接触压力为60 N，接触电流为400 A，滑动速度为400 km∕h，空气流速为5 m∕s，气压等级分别为50、70、90、101 kPa，仿真时间为1 000 ms，单步时间为10 ms，采用MUMPS 求解器，仿真计算出4 种气压等级下接触剖面温度场与速度场云图分布。

表1 不同气压条件下平均环境温度与滑板接触区域稳态平均温度对应表

图11 所示为不同气压等级与速度场之间的关系，可以看出当流速一定时，随着气压从50 kPa 增大到101 kPa，速度场最大值从4.5 m∕s 减小到4.24 m∕s。这是由于气压升高导致空气动力黏度增加，其流动性有所减弱，因此速度也会下降。图12 所示为50 kPa 气压下温度场与速度场分布特性。弓网接触部分作为稳态热源，其温度分布非常集中，而流体域所处温度较低且分布比较分散。接触区域稳态温度与环境温度差异较大，因此高温仍然集中于受电弓滑板表面。流体从左侧入口进入，因而滑板左侧的流体速度场等值线分布较集中。弓网接触部分对气流的阻断效应使滑板上表面与接触线左侧产生黏性流动，空气流动性下降，流体在接触区域左侧聚集停滞，因此速度变小。而在接触线上方气流具有较强的爬坡效应，因此在水平方向形成流场拖尾，随后又下沉在弓网接触右侧集中形成涡流。受电弓滑板下方无障碍物阻隔，因此速度等值线分布密集。

图11 不同气压等级与速度场的关系

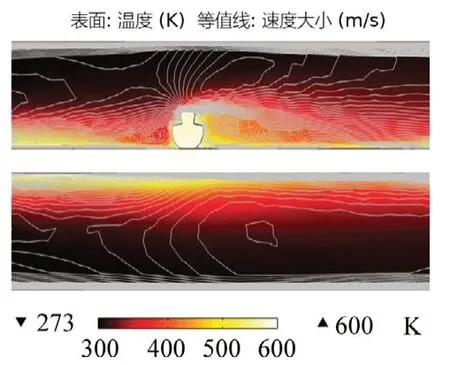
图12 50 kPa气压下温度场与速度场分布

为了研究不同气压和流速作用下弓网接触模型气体速度场的分布，设定如下仿真条件：接触压力为60 N，接触电流为400 A，滑动速度为400 km∕h，取气压等级分别为70、90、101 kPa，气体流速分别为1、3、5 m∕s，仿真时间为1 000 ms，单步时间为10 ms。

当气压分别为70、90、101 kPa时气体速度场的云图分别如图13～15 所示。当气压相同时，随着流速从1 m∕s增大到5 m∕s，接触线内部气流沿水平方向移动形成的拖尾现象更明显，体现在云图中为蓝色加深。而当流速一定时，随着气压等级从70 kPa增大到101 kPa时，接触线内部形成的蓝色拖尾在水平方向的范围逐渐拓宽。此外，当气体流速为5 m∕s时，随着气压升高，接触线背风面的低速场，即蓝色部分聚集程度降低，气体流速小时对背风面速度场的影响较小。流体入口侧在上下两端分别形成高速漩涡，旋涡中心红色加深即速度很大。受电弓滑板左端，即迎风面速度场较小，接触线迎风面速度场呈现弧形分布，与导线形状契合，背风面低速场分布集中。

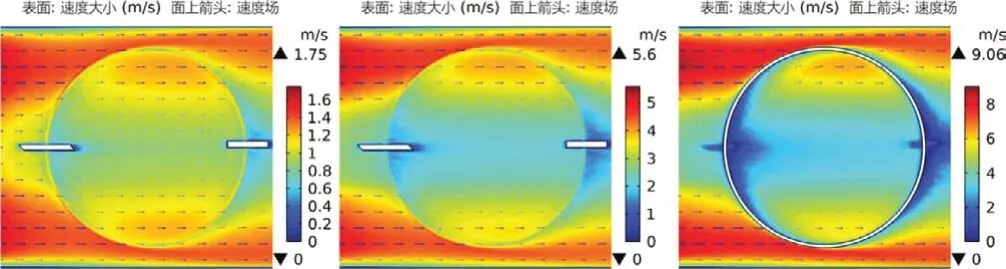
图13 70 kPa条件下流速分别为1、3、5 m∕s时速度场云图分布

图14 90 kPa条件下流速分别为1、3、5 m∕s时弓网速度场云图分布

图15 101 kPa条件下流速分别为1、3、5 m∕s时速度场云图分布

2.4 低气压条件下瞬态流场压力分布特征分析

为了研究不同气压等级对弓网接触模型的风压分布特征的影响，设定如下仿真条件：接触压力为60 N，接触电流为400 A，滑动速度为400 km∕h，空气流速为5 m∕s，气压等级分别为50、70、90、101 kPa，仿真时间为1 000 ms，单步时间为10 ms。

以气压50 kPa 为例，图16 所示为弓网系统接触模型二维切面瞬态压力的等值线云图。当t=0 ms 时滑板和接触线受到的压力主要分布在接触线左侧外部以及右侧外内部。当t=10 ms时，滑板左端受到气流冲击形成中高压区，最大压力达到6.64 Pa，接触线左外侧作为迎风面，表面压力处于高正压区，滑板另一端和接触线左内侧作为背风面处于低负压区。气流沿水平方向流动，所以接触线右内侧表面压力处于次高正压区，右外侧作为背风面处于低负压区。随着时间推移，在t=40 ms 和t=1 000 ms可以看出，表面压力等值线会更加集中并且形成明显的正压力斑，这是由于气流受到滑板和接触线的阻断产生了回流，而原本处于气流右侧的等值线继续向远离接触线侧偏移。

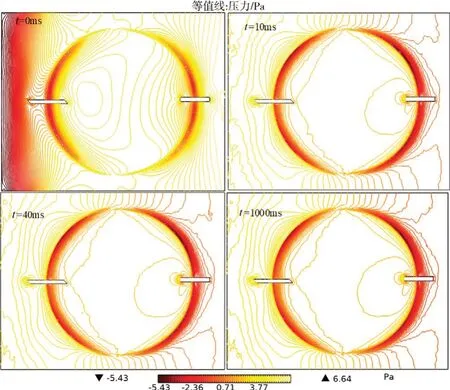
图16 50 kPa气压下切面瞬态压力等值线分布

在z轴方向上截取不同水平切面（xoy面）作为压力检测面，z轴方向上的高度取值分别为-20、-10、0、5、10、20、30 mm，如图17 所示，仿真计算了不同气压条件下z轴距离变化与对应切面所受到压力值之间的关系，如图18 所示。结果表明，随着z轴距离的增大，不同高度切面所受压力先增大后减小，环境气压与对应切面所受压力成正比。根据三维弓网滑动电接触粗糙表面接触固体域模型尺寸可知，在z轴方向距离分别为-20、-10、20、30 mm 时，对应的切面未能穿过固体模型，气流发展平稳且难以产生黏滞行为，因此受到压力较小。而z轴方向距离分别为0、5、10 mm时，对应切面以不同程度的方式横穿接触线和受电弓滑板，由于接触线刚性杆件的阻挡作用，迎风面气流冲击效应较大，所以受到压力也会增大，而在远离接触线和受电弓滑板的高度上压力再次减小。