基于车速影响的比利时路强化系数研究*
2023-11-13刘东俭朱淮烽
刘东俭,朱淮烽,施 磊,朱 遥
(中汽研汽车试验场股份有限公司,江苏盐城 224100)
0 引言
汽车试验场是进行汽车道路动态试验的场所,其中的各试验道路是将实际社会道路中的各类道路场景进行浓缩、集中、强化而形成的标准化道路[1]。研究确定各道路的技术指标,不仅是有效开展道路试验的基础,也有助于合理制定道路维护保养计划。
耐久路通过路面不平引起车辆载荷变化,从而使整车各部件发生疲劳损伤,是试验场道路场景的重要组成部分[2]。整车耐久性道路试验的一项重要工作是通过试验场各路况循环次数的合理匹配,复现用户使用条件下各部件的损伤[3]。由于悬架系统弹簧、减震器及橡胶衬套等非线性部件的存在,导致载荷传递特性的变化[4]。因此,在整车疲劳耐久试验中,损伤大小与频域分布是考核效果评估的重点关注内容[5]。在众多试验场路况中,比利时路面具备高强度连续激励的载荷特征,在整车道路耐久试验中贡献了50%以上的损伤,是道路试验中的重点关注对象。车速作为道路试验的一个重要控制因素,对于损伤大小及频域分布有决定性的影响,明晰比利时路面下车速对载荷损伤及频域分布的影响规律,对于合理有效开展整车道路试验具有重要指导意义。已有研究多以仿真模拟的方式进行强化系数计算,受轮胎模拟及整车模型精度的影响,计算结果与实车实际测得的结果相差较大。
本文以车轮六分力信号为主要通道,悬架、车身等部分关键部件的应变信号为辅助通道,研究比利时路的强化系数与车速之间的关系,以指导整车疲劳耐久试验规范的编制工作,减少因人为主观判断造成的偏差[6]。
1 疲劳寿命计算及强化系数数学模型
1.1 Basquin公式
远小于强度极限的应力循环会导致材料的疲劳失效,且应力幅值是造成金属零部件发生疲劳破坏的主要原因,应力均值对于疲劳破坏有一定的影响[7]。用Basquin 公式可定量表达出应力幅值与疲劳寿命之间的关系式。
式中:σa为应力幅值;m为疲劳指数;C为常数。
1.2 线性损伤累积准则
Miner准则认为当金属部件受到交变载荷作用后,会吸收因形变造成能量[8]。当部件受载荷σ作用N次,部件吸收的能量累积达到可使该部件发生疲劳损坏的能量上限W时,该部件即出现疲劳失效。同时部件收的能量wi与交变载荷次数ni成正比。
式中:W为使部件发生疲劳损坏的总能量;N为在载荷σ作用下使部件发生疲劳损坏的总循环次数;wi为实际吸收的能量;ni为实际的载荷循环次数。
当wi=W时,部件发生疲劳损坏。因此,当部件依次受σ1,σ2,σ3,…,σn载荷水平作用时,各载荷水平作用下的疲劳寿命依次为N1,N2,N3,…,Nn。在汽车耐久性工程应用实践中,可根据式(3)计算汽车部件受不同载荷水平的循环加载后的累积疲劳损伤D:
损伤与载荷循环次数成线性关系,且在各级载荷作用下的损伤之和为1,即D=1 时发生疲劳损坏。在计算过程中若根据材料实测S-N曲线进行计算,得出的损伤值为真实损伤。在工程实践中,一般通过标准S-N曲线进行计算,将应力、应变等作为广义应力进行计算,得出的损伤值为名义损伤,或称为伪损伤[9]。
1.3 强化系数数学模型
广义的强化系数指当车辆发生同等失效时,车辆在普通社会道路行驶里程与试验场强化道路行驶里程的比[10],道路载荷下强化系数可通过不同载荷损伤线性累积量进行研究[11]。
当已知部件的S-N曲线的Basquin公式,即已知车辆部件的疲劳极限为σ-1,等幅加载下的疲劳寿命为N0和疲劳指数为m。则可知部件在任意的载荷σi加载下的疲劳寿命Ni为:
因此当得到车辆在长为L1的社会道路行驶的载荷时域信号时,根据Miner 准则可知车辆在该社会道路行驶的累计损伤D为:
车辆在该社会道路内行驶的单位里程的损伤D0为:
根据Miner 准则可外推出,当D=1 即车辆发生疲劳损坏时。车辆在该社会道路持续行驶至车辆发生疲劳损坏的总里程L为:
因此,可进一步外推。强化系数即当车辆发生同等失效时,车辆在普通社会道路行驶的总里程L与试验场强化道路行驶的总里程L′的比K为:
式中:L1′为车辆在试验场强化道路行驶的里程;D′为车辆在该试验场道路行驶的损伤。
以上公式给出了任意两段道路的强化系数计算方式,同时可推导出强化系数也为车辆在两段道路行驶时单位行驶里程造成的损伤之比。
2 载荷谱采集与处理
2.1 试验车辆及传感器的安装布置
由疲劳损伤的产生机理可知,强化系数与试验道路、车辆配载、驾驶方式等外因密切相关。本文以某中型SUV 为测试车辆,配载状态设定为半载,其中前轴质量为1 132 kg,后轴质量为1 020 kg。通过采集轮心六分力、车身风险点位置应变、悬架杆件载荷,开展车速对比利时路面强化系数影响研究。传感器局部安装位置图如图1所示。受力载荷名称及传感器参数如表1所示。

图1 传感器局部位置安装示意图
2.2 试验道路及工况的确定
对试验场的道路进行组合使用,用于模拟用户社会道路,以得到社会道路的单位里程损伤作为标准损伤。用于模拟社会道路单位里程损伤的试验场行驶工况及里程比例如表2所示[12]。
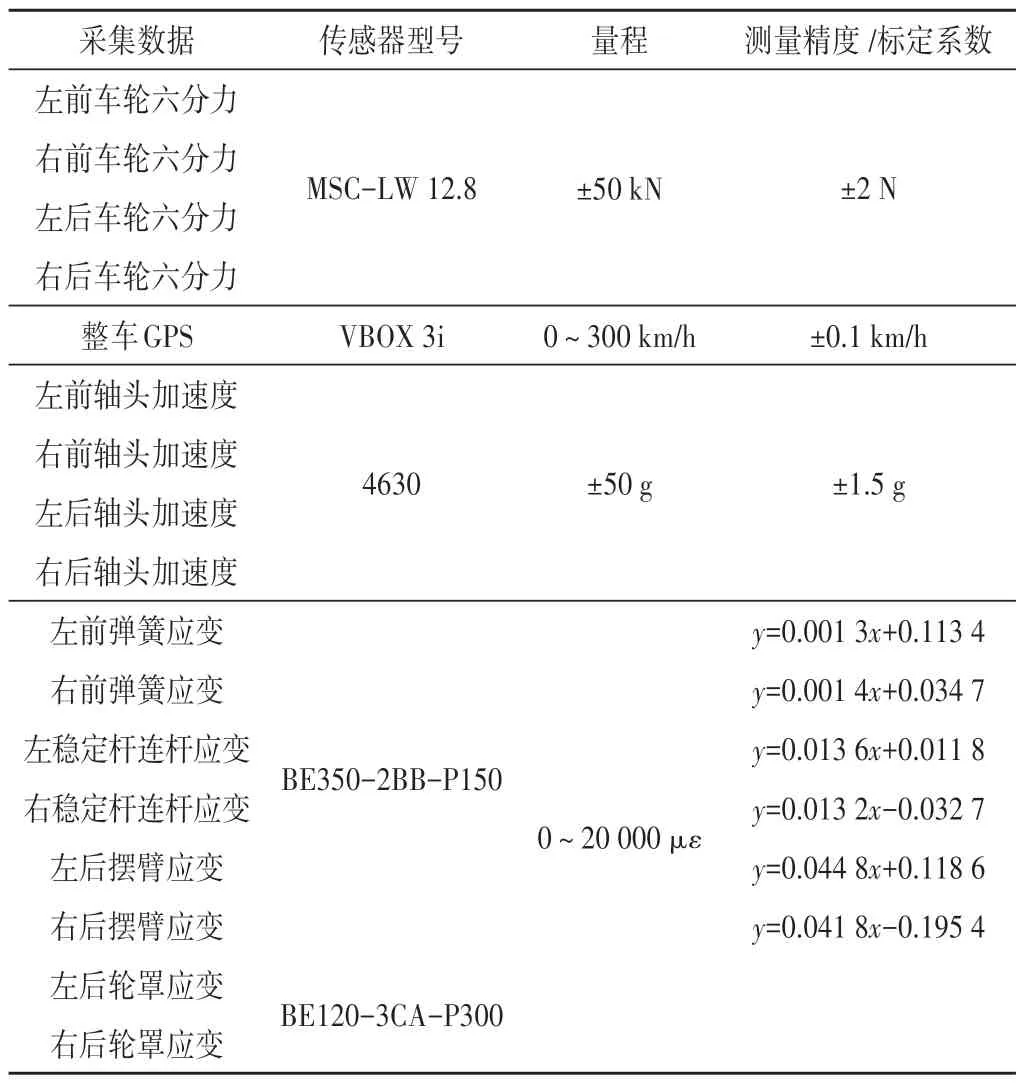
表1 受力载荷名称及传感器参数

表2 用于模拟社会道路行驶的试验场行驶工况
试验场中比利时路的道路参数及车辆行驶速度如表3所示。

表3 比利时路参数及行驶工况表
2.3 数据的采集与处理
为保证后续数据处理结果的准确性,并覆盖同一路面多次驶过后的分散性,在各试验道路进行不少于3 次的行驶并采集时域信号。所采集的载荷谱信号在经过去除毛刺、纠正漂移、工况截取、低通滤波等操作后,可再对信号的有效性进行分布特性检验,以提高后续进行频域损伤关联计算工作的可靠性[13]。
2.3.1 频域分析
对采集的数据进行功率谱分析,以判断引起车辆发生疲劳损伤的主要载荷频段,并对复杂的道路载荷数据选择合适的滤波方式。对采集的用户道路及比利时路的轴头加速度、弹簧应变进行功率谱分析如图2~5所示。
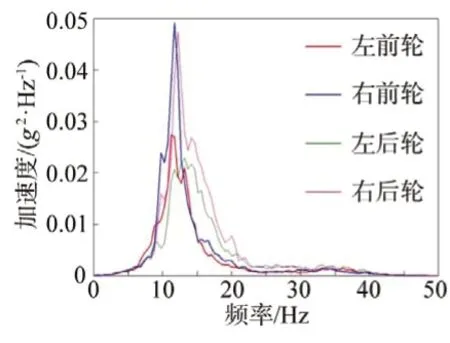
图2 用户道路车轮轴头加速度功率谱
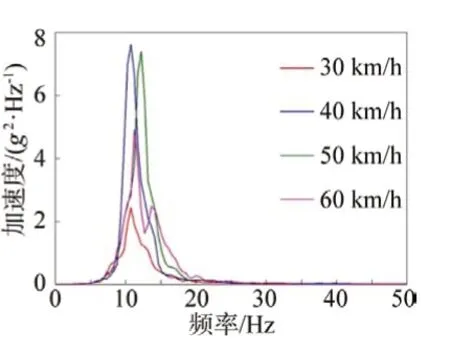
图3 比利时路左前轮轴头加速度功率谱

图4 用户道路弹簧应变功率谱
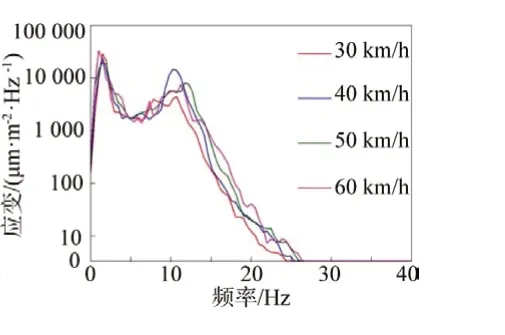
图5 比利时路左前弹簧应变功率谱
通过功率谱的分析显示,所有通道载荷频段主要在30 Hz 以下,其余频段载荷功率较小,说明30 Hz 以下载荷在整体损伤中贡献量最大。通过多个载荷通道功率谱综合分析,可以确定50 Hz 以上频段功率谱密度非常小,可以直接忽略。另外,不同部位载荷具有很明显的频带分布特征,并路面激励(轮心加速度)主要集中在5~20 Hz,簧上质量载荷响应频段主要集中在0~5 Hz,簧下质量载荷响应频段集中在5~20 Hz,而弹簧作为簧上质量、簧下质量连接件,在0~5 Hz 和8~15 Hz 内具有明显的双峰特征。由此可见车辆的损伤主要来自于因路面不平度而造成的车辆损伤,其载荷频率多处于中低频段。
2.3.2 数据分布特性检验
车辆耐久性载荷具备连续分布的特征,目前有诸多统计分析方法可有效地对数据进行连续性检验,本文以卡方拟合优度检验方法对采集的载荷进行连续性分布检验[14],鉴于论文篇幅原因,以左前车轮垂向力为例进行说明。
将采集的n个数据xi(i= 1,2,3,…,n)根据大小排序分为m个等距区间 [Xj,Xj+1)(j= 1,2,3,…,m)。
左前轮垂向力频次分布直方图如图6所示。
统计采集数据xi(i= 1,2,3,…,n)落在每个区间的个数kj(j= 1,2,3,…,m),则数据落在各区间的频率为kj∕n。根据采集数据的频次特征(图6),初步判定数据服从正态分布,则有:

图6 左前轮垂向力频次分布直方图
正态分布函数F(X) 为:
F(X)在区间[Xj,Xj+1)内的概率Pj为:
则频率kj∕n与正态分布F(X)的概率Pj之间的总偏差统计量D为:
正态性检测计算的统计结果如表4所示。
在进行正态性检测时,取其显著水平α=0.05,自由度m=30,根据卡方分布临界值表可知,得到的临界值为43.77[15]。因此,左前车轮垂向力数据的总偏差D=0.009 857 126远小于临界值43.77,检验的载荷数据符合正态分布特性,与图6载荷频次分布直方图一致。
3 比利时路强度系数计算
3.1 用户道路行驶单位里程伪损伤计算
将单位里程设定为10 km,根据里程分配比例对采集的数据进行筛选并进行截取以获得用户道路行驶的单位里程载荷谱。图7以左前车轮垂向力为例展示了单位里程载荷谱的获取过程,其余通道的单位里程载荷谱可按此方法获取。
路面强化系数表征了车辆在两段道路行驶时单位行驶里程造成的损伤之比,因此在计算过程中的相对损伤对比是强化系数确定的最直接判断依据。将六分力作为主要通道进行损伤计算。根据截取的用户道路行驶单位里程载荷谱使用前文公式对各主要通道进行损伤计算,结果如表5所示。
3.2 比利时路单位里程伪损伤计算
比利时路长度为500 m,将在比利时路采集的六分力信号进行雨流计数后再按里程比例外推至10 km 以获得比利时路单位里程的雨流计数直方图。图8 以左前轮垂向力为例展示了车辆以60 km∕h的速度行驶时比利时路单位里程载荷谱的雨流计数直方图。

表4 左前车轮垂向力数据正态性检测计算结果
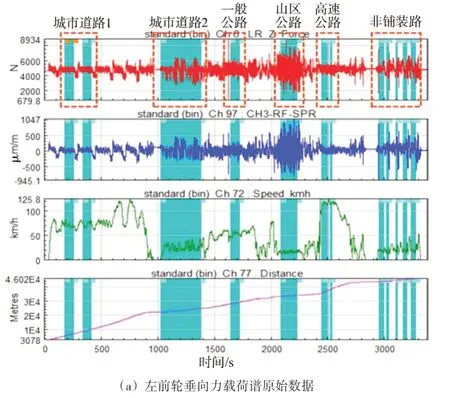
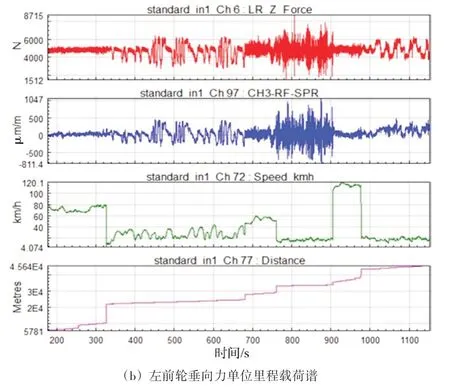
图7 左前轮垂向力单位里程载荷谱截取
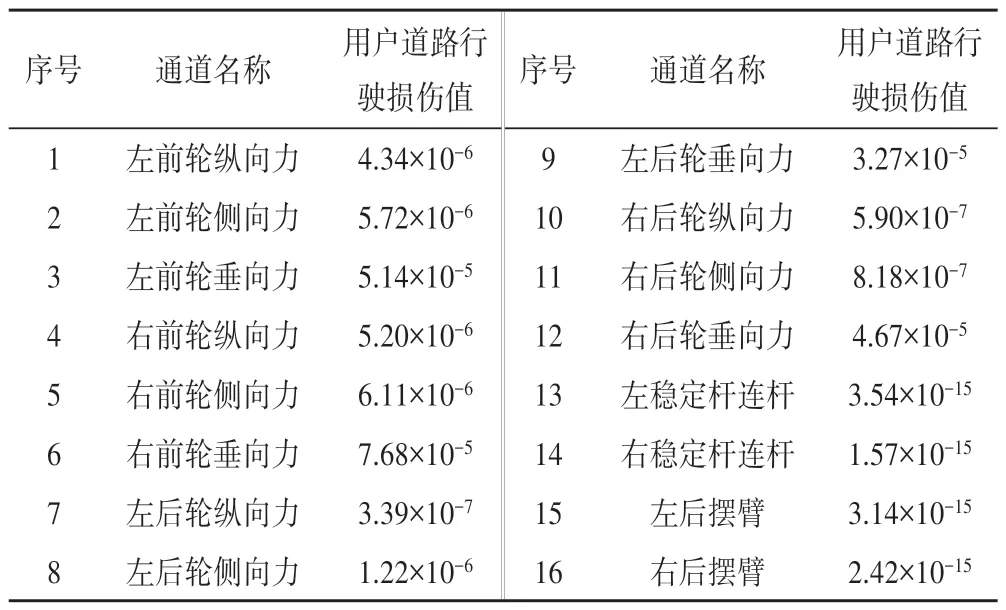
表5 用户道路行驶的各通道损伤值

图8 左前轮垂向力单位里程载荷谱雨流计数直方图
将车辆以各车速在比利时路行驶时采集的各通道载荷谱外推至单位里程,对各通的损伤进行计算,结果如表6所示。
3.3 比利时路强化系数
将用户道路行驶单位里程的六分力损伤作为标准损伤,即强化系数为1。将车辆的六分力信号作为主要通道,得出车辆在比利时路行驶时的强化系数与车速的关系如图9所示。
比利时路对整车的强化效果较为显著。特别是垂直方向的强化系数较为明显,范围为43.3~379.6,对车辆的纵向方向强化系数范围为6.1~66.2,对车辆的侧向方向强化系数范围为0.3~42.1。
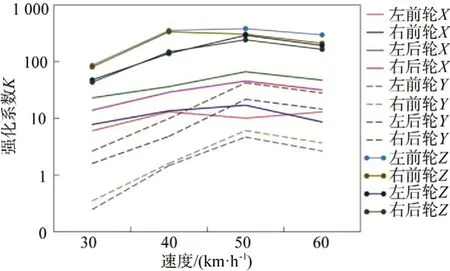
图9 比利时路强化系数与车速关系
比利时路强化系数与车速有关,总体表现为强化系数随着车速的变大而变大,并在车速为50 km∕h时达到峰值,随后逐步下降。
比利时路对整车在纵向及侧向的强化效果一般,这是由于在模拟用户道路行驶时,需根据试验场道路布置及驾驶要求进行行驶,因此在城市广场及盘山坡道行驶时有较多的转向与制动操作。而比利时路虽设置了纵坡及弯道,但行驶过程中缺少足够数量的转向与制动工况,导致其对车辆在侧向及纵向的考核较垂向考核的强度弱。
选取左稳定杆连杆、右稳定杆连杆、左后摆臂、右后摆臂作为辅助通道,比利时路对各辅助通道的强化系数与速度之间的关系如图10所示。
各辅助通道的强化系数范围为2.5~151.1,其变化趋势与主通道强化系数变化趋势一致。

图10 各辅助通道的强化系数与速度关系
4 结束语
频段在30 Hz 以下的载荷对整车的损伤贡献最大,频段在50 Hz 以上的载荷对整车的损伤较小,在工程运用中可忽略。
比利时路的强化效果较为明显,其强化系数的范围约为43.3~379.6,且随着车速由30 km∕h 增加至60 km∕h的过程中,强化系数先增大后减小,且在车速为50 km∕h时达到峰值。
车速在40 km∕h以下时,强化系数上升缓慢;车速从40 km∕h 增加至50 km∕h 时,强化系数上升明显加快;车速从50 km∕h 增加至60 km∕h 时,强化系数下降明显加快。
强化系数与轮荷有关,在同样的试验工况下,轮荷越大强化系数越大。强化系数是一个变量并非固定值,其与车辆配载、车速、对比通道等均相关,整车或零部件企业应选取适合的试验工况对其产品进行验证。
