基于电流丝法的多级线圈发射装置滑差与线圈匝数匹配特性研究

王启鉴,赵文龙,牛小波,胡元潮,黎 鹏

(1.三峡大学 电气与新能源学院, 湖北 宜昌 443000;2.中国人民解放军空军研究院, 北京 100000;3.山东理工大学 电气与电子工程学院, 山东 淄博 255000)

0 引言

电磁发射装置(EML)技术以其超高初速、易控性和能量安全等优点引起了学者们的广泛关注[1]。近年来,世界范围内的电磁发射技术实现了跨越式发展:在军事领域,电磁发射装置被广泛认为在航空母舰弹射、舰载武器超远程压制和精确打击、中短程防空和反导等方面具有较好的效果[2],在一定程度上,电磁发射技术代表了未来舰艇装备的发展方向[3];在民用领域,采用电磁发射技术的超高速磁浮列车具有较好的应用前景,2022年10月,世界首个电磁推进地面超高速试验设施,在中国济南建成的“电磁橇”可以把超过1 t的物体在短时间内从0加速到1 030 km/h,电磁发射技术在社会灾害救援,非爆破定点抛投,火灾消防等领域具有长足的发展空间[4-5]。

多级同步感应线圈炮(multistage synchronous induction coil-gun,MSSICG)作为电磁发射装置的重要部分,利用磁悬浮效应可以实现较高的能量转换效率,避免负载与筒体之间的烧蚀和磨损[6]。此外,从其推进原理来看,通过适当增加驱动线圈,调节驱动电流的幅值和脉冲宽度,可以获得高初速和长射程[7]。然而,目前研究主要集中在多级同步感应线圈发射器在大质量负荷低速推进中的能力,而对其中高速应用场景的研究却很少。造成这种现象的原因有很多,其中,最重要的是现有的仿真模型在中高速MSSICG的快速有效方案设计方面存在不足[8],其结构与关键影响因素仍然有待进一步探究,尤其是影响中高速MSSICG发射效率的滑差与线圈匝数的匹配问题,相关文献尚未给出规律性的结论[9-10],该问题有待进一步探讨。

本文中针对中高速MSSICG的数值模拟建模和设计策略进行了探讨,分析了不同结构参数对电枢加速度的影响规律,阐明了高速发射器滑差与匝数匹配关系,并在7级和25级同步感应线圈发射器仿真算例中进行验证。

1 MSSICG的数学模型

1.1 MSSICG的机电结构

同步感应线圈炮(synchronous induction coil-gun,SICG)产生强磁场是对铁磁弹丸或铁磁电枢组件进行加速的首要前提,单级SICG尚未达到军事应用的标准,目前仅用于民用低速和轻量化特定设备的助推器。为了使其具有攻击能力,通常采用多级驱动线圈将电枢弹丸连续推向高速[11]。MSSICG的结构如图1所示。若干个集成的分节式驱动线圈同轴堆叠在绝缘筒体上作为电枢,每个线圈通过同轴电缆与单独的电容器相连。串联可控晶闸管可实现供电顺序的精确调节。负载侧的高压硅堆不仅防止了电感负载引起的电压反转而损坏电容,而且阻断了前一级线圈产生的感应电流[12],电枢在多级线圈的连续电磁力推进下实现连续加速,最终获得可观的发射速率。

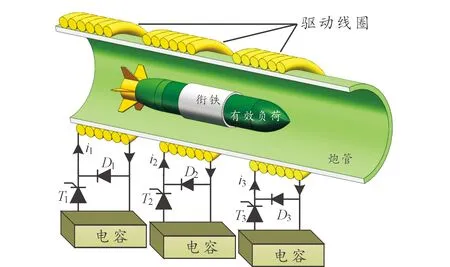
图1 MSSICG三维原理图

1.2 等效模型

早在20世纪90年代,国内外研究者就初步构建了MSSICG理论体系,其机械结构和发射特性已在多个国家的研究样机中得以证实,三维有限元计算方法及商业化软件的涌现,使得MSSICG的三维精细化建模成为可能。由于MSSICG运行是一个集电磁、传热、运动、变形为一体的多物理动态耦合过程,为了衡量建模的准确性和便捷性,有必要对建模过程做出以下理想化的假设:① 只考虑温升对电阻率的影响,忽略了温升对导电体电感和密度的影响;② 不考虑电枢和驱动线圈继续承受径向力时的形变,忽略炮管内电枢的横向偏移和自转;③ 忽略由瞬变磁场产生的高频磁场的作用。

由于励磁电流会导致感应涡流在电枢轴向截面上分布不均匀。为此,引入了该领域常用的电流丝法(current filament method,CFM)来简化变系数非线性常微分方程初值问题的模型求解[13],上述假设为引入CFM构建集总参数电路等效模型提供了简化条件。

1.3 建立模型

用基尔霍夫定律来描述各电流丝的电压平衡关系为[14]

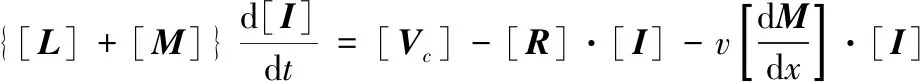
(1)

式(1)中:x和v分别为弹丸的位置和速度;[L]为由自感组成的对角矩阵;[M]为由互感组成的对角矩阵,是相对于机械动能和焦耳热电磁能转换的桥梁;[R]为由线圈电阻和电流丝电阻形成的对角矩阵,其中,每个元素是由式(2)描述的绝热状态下的焦耳热确定的瞬态值,即

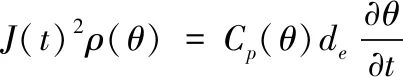
(2)

式(2)中:J(t)和de分别为电流密度和导体密度;ρ(θ)和Cp(θ)为随温度变化的电阻率和比热容,两者与温升的关系可表示为

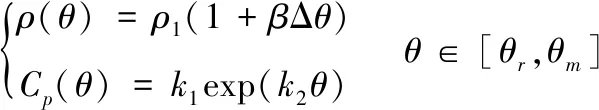
(3)

式(3)中:θr和θm分别是导体的室温和熔化温度。β为电枢用6063型铝合金的电阻温度系数。系数k1和k2分别为0.819和3.07×10-4。

用虚功原理和达朗贝尔原理来描述弹丸的运动特性,可得

(4)

式(4)中:ma为弹丸质量;x0为电枢的初始位置。线性电容器的伏安关系为

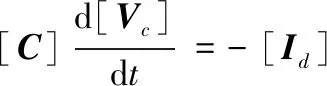
(5)

式(1)—式(5)所构建的数学模型的有效性已在许多文献中得到证实。但工程实际中的基于该模型的模拟试验或者样机设计,仍然多采用人工逐步调试或者基于仿生智能算法的迭代优化。由于多物理场耦合作用下的边界条件过于复杂,当线圈级数较多时,同步感应线圈发射器的迭代计算仍有一些不能收敛的问题。

2 MSSICG的滑差与匝数计算

2.1 MSSICG的滑差计算

旋转电机根据转子与合成旋转磁场是否同向同速旋转可分为同步电机和异步电机。MSSICG的同步特性意味着驱动线圈的馈电时间必须与直线运动电枢的位置精确匹配。虽然物理意义和运行方式有很大不同,但作用在其动子上的电磁力是由复合磁场与导磁负载的相对运动产生的。从广义角度来看,MSSICG本质上属于异步直线电机的范畴,因此,旋转电机中的滑差概念可以为MSSICG的发射特性优化提供参照。

通常,旋转电机的合成旋转磁场用其峰值的运动来量化,峰值出现在峰值相电流流过的绕组的轴上[15]。与此类似,MSSICG的第k个驱动线圈对应的直线磁行波(linear magnetic traveling wave,LMTW)的速度可以表示为

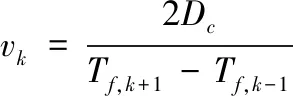
(6)

式(6)中:Dc为相邻2个驱动线圈的中心距;Tf,k为k级线圈的峰值时间。假设k级线圈峰值时刻的电枢速度为va,k,则滑差速度应表示为

vslip=vk-va,k

(7)

式(7)中:vslip为峰值时刻LMTW与电枢之间的速度差,LMTW的峰值出现在线圈轴上。因此,线圈轴与电枢尾部之间的距离可以定义为滑差距离:

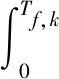
(8)

式(8)中:Zc,k为k级驱动线圈的中心位置;Zp,k为电枢尾部在峰值时刻的位置。假设在瞬态脉冲电流上升期间电枢的速度大致恒定,可推导出上升距离为

δk=Zp,k-Za,k=

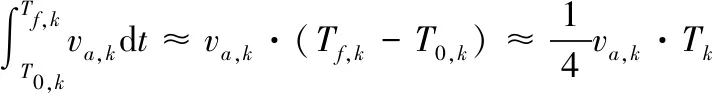
(9)

式(9)中:Za,k为放电时电枢尾部的位置;T0为k级放电电路的电流周期。在确定匝数之前,无法提前估计Tk,从而导致Zp,k未知。因此,结合式(8)和式(9)消除Zp,k,得到预测电枢加速时间的等式:

Za,k=Zc,k-Zslip-δk=

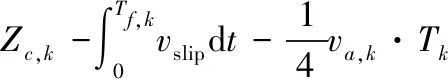
(10)

2.2 线圈匝数计算

式(10)体现了触发时刻与放电周期的相关性,因此,可以采用放电周期与匝数的关系来构造触发时刻与匝数的相关性,进而确定它们的匹配特性。

RLC串联谐振电路的放电周期可表示为

(11)

式(11)中:Lk和Lk,d分别为k级线圈的自感和等效单匝电感,Ck为k级线圈对应的电容值。

为了计算方便,假设所有级线圈的电枢上升距离相等。此外,同时驱动电枢的几个线圈是保持相当平稳加速的可行方式。因此,线圈的上升距离与中心距应满足关系式:

δk=εDcε∈(0,1]

(12)

最后,结合式(9)、式(11)和式(12)可以计算出k级线圈的匝数:

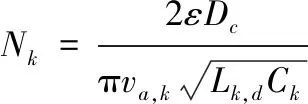
(13)

3 滑差和匝数的匹配特性

由于MSSICG的多物理场强耦合特性,不同级数和结构的发射器体现出较大的运行性能差异。其能量转换关系的推导表明:电磁推力取决于互感梯度、驱动电流和感应涡流。在恒功率供电的情况下,触发时机和匝数对上述3个因素的调节起关键作用。因此,放电间隔和匝数的匹配在MSSICG的设计与运行控制中具有重要意义。

3.1 不考虑匹配特性的情景分析

当不考虑放电间隔和匝数的匹配特性时,在这种情况下,所有线圈的几何参数是一致的。仿真采用的7级发射装置的结构和电气参数[16-17]如表1所示。同时,按照图2所示的流程调试了其相对最优的触发定时,此外,根据上述计算过程得出的放电间隔是否最优取决于调试步长及调试次数。

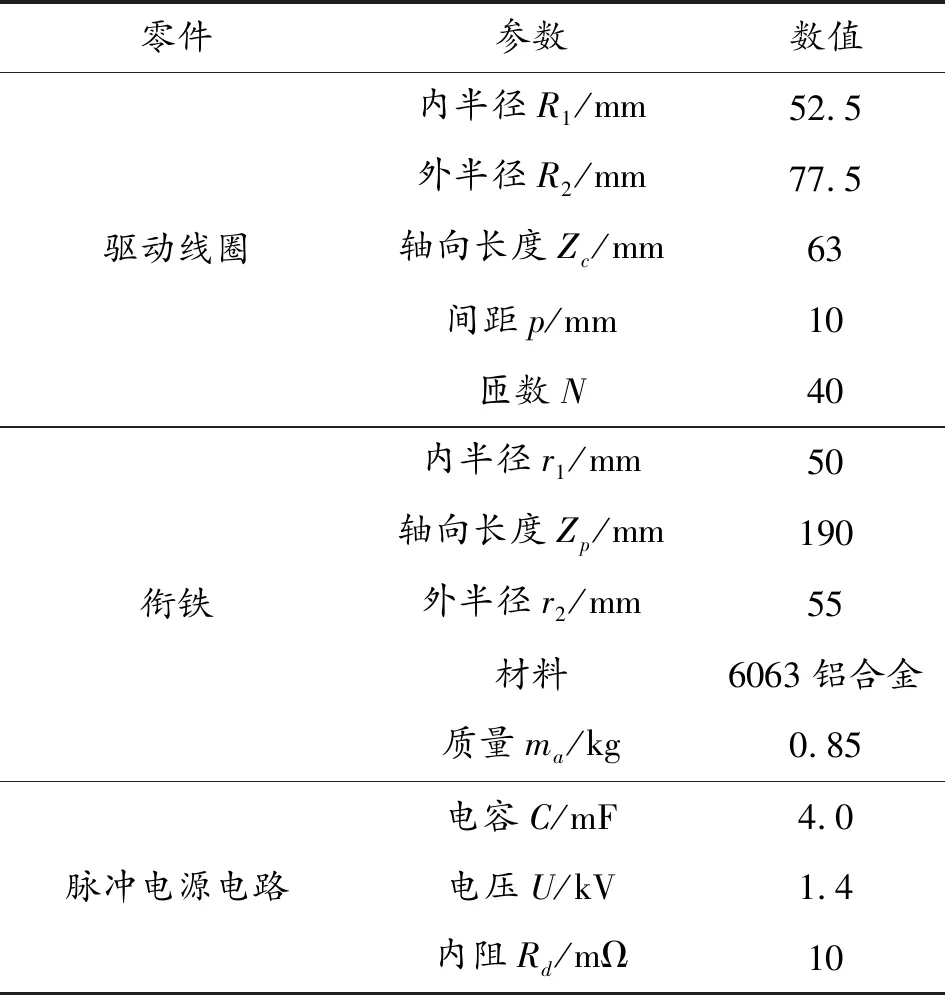
表1 仿真模型的结构和电气参数

图2 不考虑匹配特性的MSSICL计算过程

根据表3所示的仿真计算条件,经过迭代计算得到线圈产生的电流和电枢速度如图3所示。

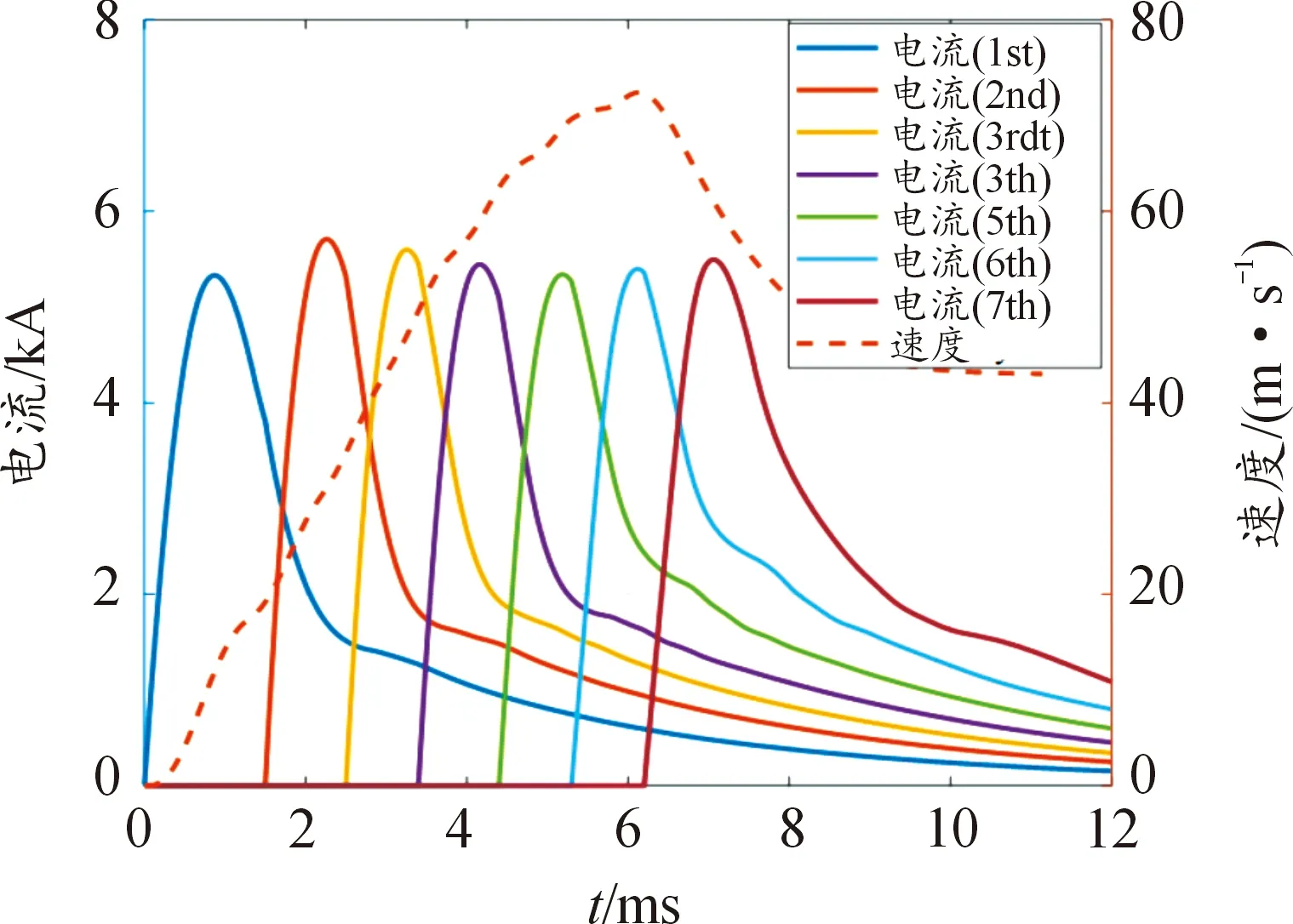
图3 考虑耦合效应的放电电流波形

从相应波形中采集放电时间T0、峰值时间Tf、峰值时刻电枢速度va,计算结果如表2和图4所示。

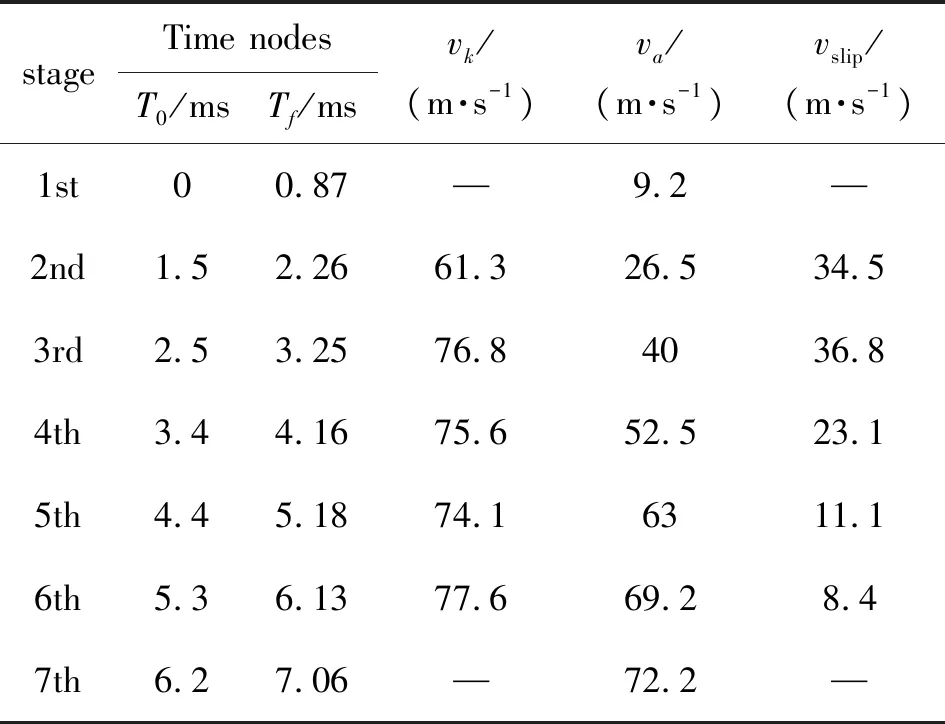
表2 峰值时间的放电时间和电枢速度

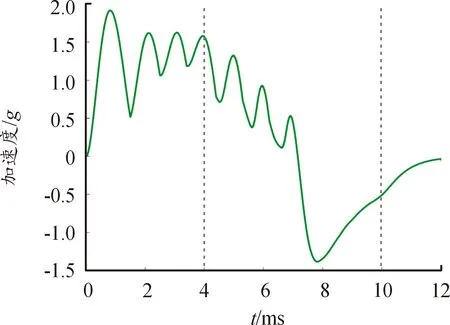
图4 电枢的加速度波形

由表2和图4可以看出,电枢的加速度趋于下降,而滑差量逐渐减小。产生这种现象的原因不仅是由于在突然加速阶段LMTW没有得到稳定,更重要的原因是电流的脉宽和幅值没有得到有效匹配,该结论为后续匝数调整提供了依据。

3.2 考虑匹配特性的情景分析

当考虑放电间隔和匝数的匹配特性时,每个线圈的几何参数和匝数都不同,仿真采用的25级SICG的结构和电气参数如表3所示。

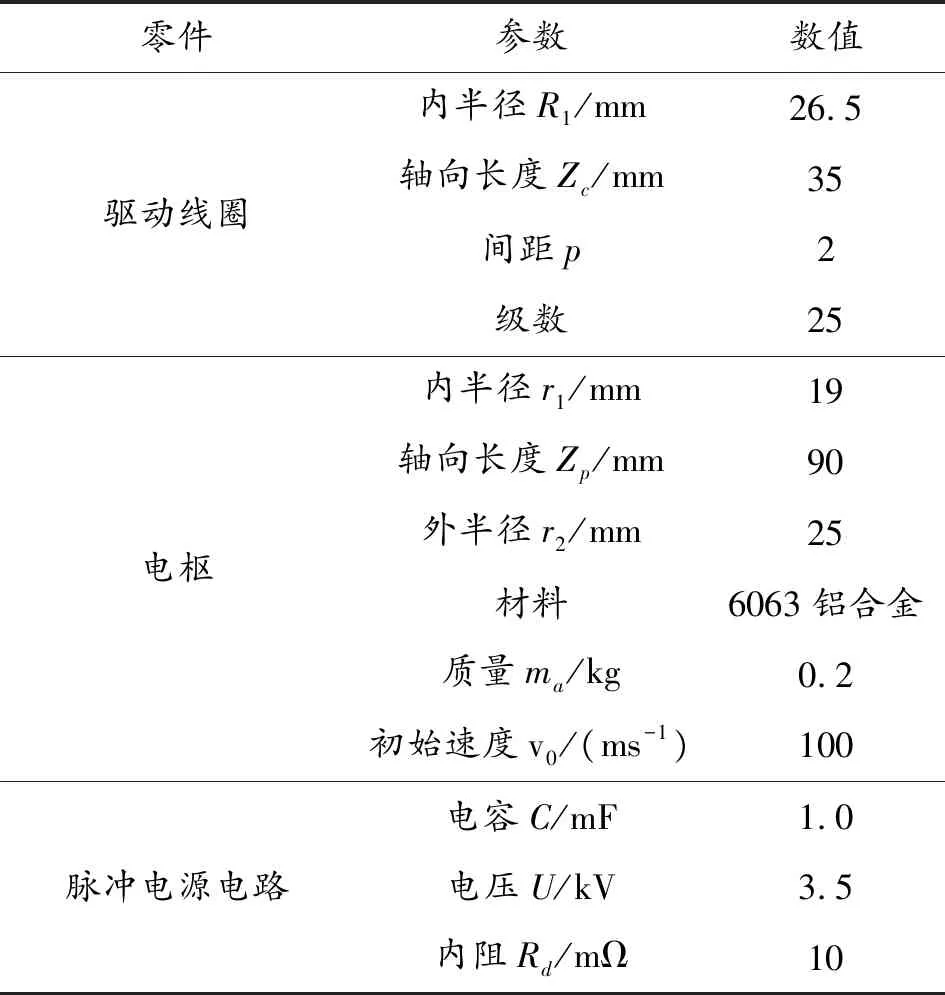
表3 25级SICL的结构和电气参数

为了避免繁琐的逐步参数调试,除指定计算等效单匝电感的第一级线圈匝数和尺寸外,其余线圈的匝数和触发时序均按图5所示程序自适应计算。

图5 考虑MSSICG匹配特性的计算流程

图5所示的计算步骤实现了“电磁-机械-热动力”耦合下匝数和触发时序的快速自适应计算。同样,通过更新线圈尺寸来修正等效单匝电感,进而可构建逐级线圈发射速率计算模型。此外,从表2的计算结果可知:滑差速度的不断下降引起电枢加速度的明显下降,将对推进效果不利。因此,假设了如图6所示的3种有上升趋势的滑差速度方案,有利于减缓电枢加速度的下降速率。

根据3种滑差速度方案,分别计算3种匹配关系下的电枢速度,得到3种滑差速度对应的电枢运动特性曲线如图7所示。此外,通过仿真计算,25级SICG采用相同的自适应计算的匝数变化趋势如图8所示。

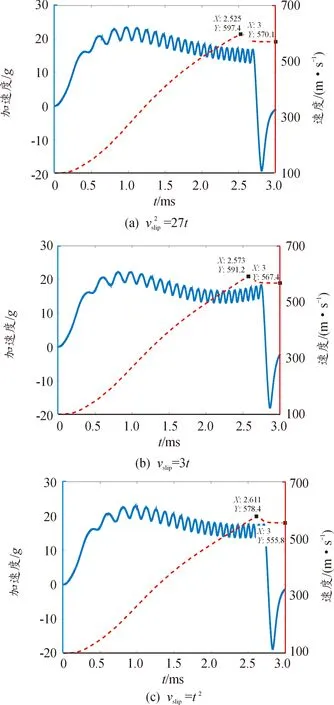
图7 不同滑差速度下的电枢速度和加速度曲线

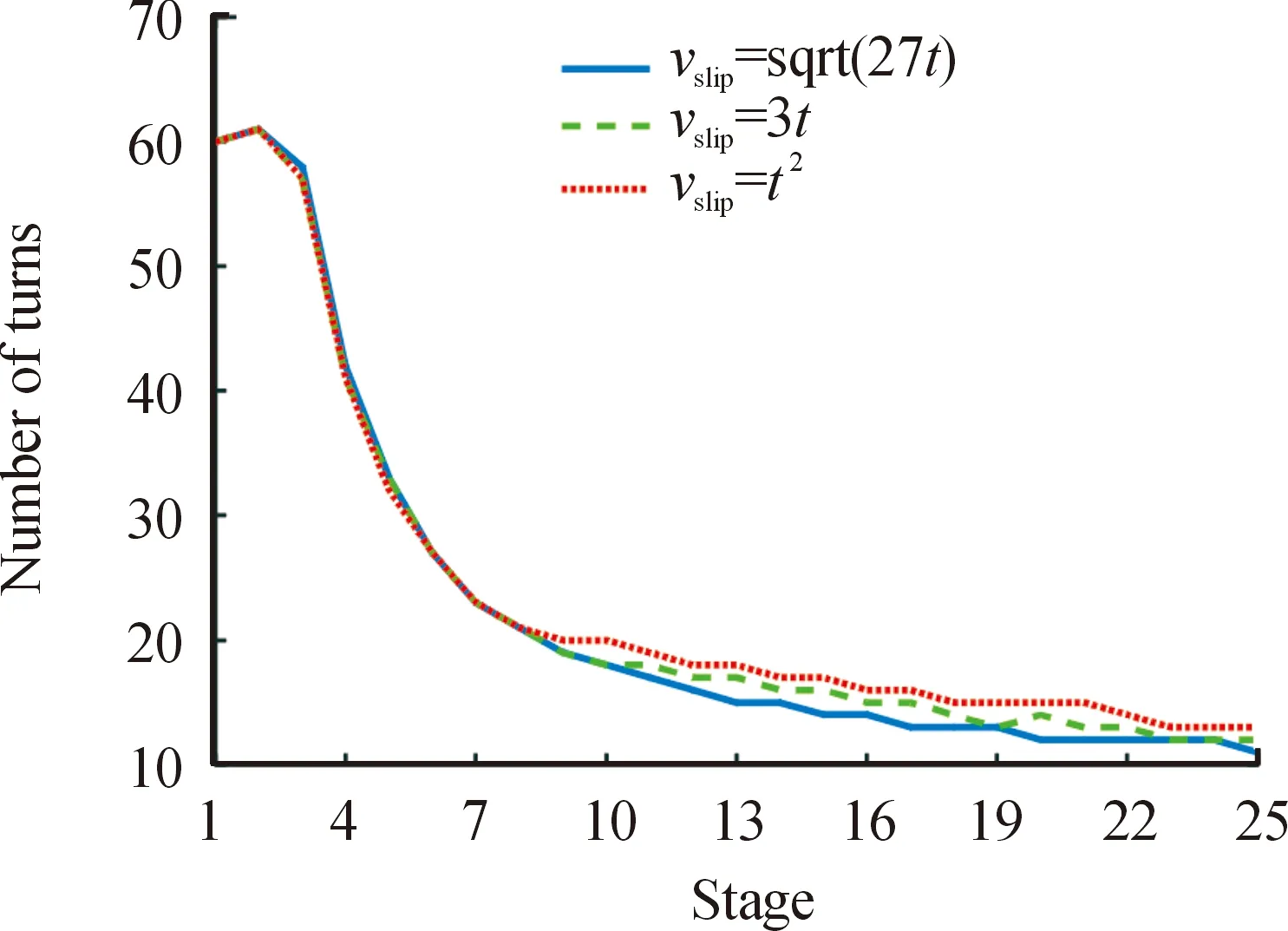
图8 各驱动线圈匝数

根据25级SICG不同滑差速度下的电枢速度和加速度变化规律可知:

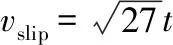
2) 当vslip=3t时,发射后期的加速度逐渐稳定,甚至出现上升趋势。但是,峰值速度和初速都略低于前一种情况。这是因为较低的滑差不利于电枢的快速加速,导致从式(13)得到的线圈匝数更多,因此,大部分时间加速度较低,随后的瞬时抬升只会减弱电枢退出后的阻力效应,使得发射过程更加平稳。

3) 当vslip=t2时,电枢的峰值速度和出口速度是3种情况中最低的。出现这种现象的原因与第2种情况类似,只是加速度尚未呈现上升趋势。

4 结论

基于电流丝法对7级和25级同步感应线圈发射器进行仿真,研究中高速发射器设计中滑差与匝数的匹配特性,得到规律性的结论如下:

1) 利用滑差确定触发时机可以作为中高速SICG参数设计和结构优化的切入点。

2) 如果不考虑滑差和线圈匝数的匹配关系,则电枢的加速度波动较大,并伴有急剧下降和明显的阻力效应。

3) 不同的滑差速度有不同的匹配效果,设置适当的线性分布滑差可以在一定程度上将加速度反向,从而平滑整个加速过程。因此,线性分布相比抛物线分布的峰值速度及出口速度更高。