基于随机权重的粒子群算法的串补配置优化

2023-11-11严俊张函尹冬晖

云南电力技术 2023年5期

严俊，张函，尹冬晖

（1. 南方电网供应链（云南）有限公司，云南昆明 650000；2. 中国南方电网有限责任公司超高压输电公司昆明局，云南昆明 650000）

0 前言

输电线路串补技术能改善长距离输电线路的电抗特性，缩短输电走廊的电气距离，提高输电系统的输电容量，提高输电系统的稳定性[1-3]。当线路的串补度过高时，会在线路末端并联大量的无功补偿[4]，导致系统电压过高，电压质量降低；当线路的串补度过低时，会导致串补电容器投入的效果不佳，降低线路输送容量。针对串补的定容选址的研究，文献[5] 对SVC和TCSC 选址定容的问题进行了研究，但是没有考虑电力系统的经济性。文献[6]以灵敏度的排序作为串补的安装地点，没有进一步考虑多目标的优化问题。文献[7]以费用为目标函数，对串补配置的地点和容量进行分析研究，但是差分进化算法的成熟度不够高。为了提高线路的输电能力，提高系统电压质量，降低网损，本文提出采用随机权重的粒子群算法，对系统的串补位置、串补度选择进行综合优化选择，达到对电力系统的潮流优化，提高系统电压稳定性。

1 加入串补的电力系统潮流计算

1.1 传统电力系统潮流计算

复杂电力系统的潮流求解是一个求解多元非线性方程的问题。牛顿拉夫逊算法是一种重要的潮流计算方法，但是潮流的收敛性非常依赖潮流初值的选择，坏的初值会造成潮流的收敛性变差甚至不收敛。为了解决潮流收敛性的问题，本文结合BPA 软件潮流求解思路，采用综合潮流计算方法，首先将网络用PQ 分解法进行迭代计算，将计算的结果作为初值转入到牛顿拉夫逊算法中进行网络潮流计算。这样既能保持PQ 分解法计算快的特点又能保证牛顿拉夫逊算法潮流收敛快的特点。

1.2 加入串补的潮流修正计算

电力系统加入串补后，改变了线路的电抗，忽略电磁暂态过程，采用阻抗模型，即在输电线路中加入电抗可调的TCSC 设备，实现输电线路电抗可调，该模型能够保持原有网络特性[8]。线路采用阻抗模型的TCSC 如图1。

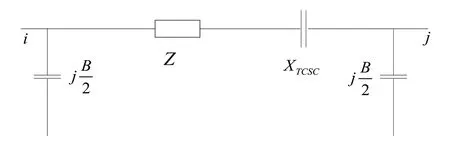
图1 线路加入TCSC稳态等效模型

TCSC 向系统节点i(j)注入的有功功率和无功功率分别为：

从上式可以看出加入串补可以调节线路有功功率和无功功率，在潮流计算中，对潮流求解公式进行修正。含有串补的支路节点功率平衡式如模型（3）所示。

2 基于随机权重的粒子群算法优化模型

2.1 多目标优化函数模型建立

系统中加入了串补主要是改善了系统电压质量和减小系统网损，当优化串补配置时选取电压质量最优和网损最小为机网协调优化串补配置的目标。

2.1.1 建立目标函数

为了解决多目标寻优函数的困难，本文建立基于权重的多目标优化目标函数，将多目标函数转换为单目标函数。

首先，根据电压的偏差建立电压质量最优的目标函数。

式中：ΔU为系统电压偏差；Ui为节点i电压；UN系统电压额定值。

其次，根据线路的损耗建立网损最小的目标函数。

式中：P为系统损耗；ΔPi为线路i的电压损耗。

最后，采取标幺值计算，统一两者单位，建立基于权重的多目标优化目标函数。

式中：λ1，λ2为电压偏差和损耗权重系数。

在电力系统中，电压质量和系统网损都是电力系统优化运行的重要指标，因此本文在权重的选取时，λ1=λ2=0.5。

2.1.2 串补配置的约束条件

机网协调优化串补配置是基于系统潮流稳定进行的，对于系统优化等式约束需要满足网络潮流方程，有功潮流和无功潮流如下式：

本文仅考虑串补装置稳态阻抗模型，串补装置投入后，串补的阻抗如下式：

串补加入的控制变量模型如下所示：

式中：Xi为第i条线路上的串补标记，只能整数且只能为0 或者1，0 代表为第i条线路上没有串补，1 代表为第i条线路上有串补；ki为第i条线路上的串补度，Xi为第i条线路上的电抗，kimin，kimax为其变化范围的上下限。

同时，还要满足系统串补的数量，其等式约束为：

式中：N为系统中加入的串补数量。

为了协调发电机和网络的关系，需要将发电机的出力控制在合理的范围内，以发电机的有功出力作为约束条件，如下式所示：

式中：Pi为发电机i的有功出力；Pimin为发电机i的有功出力的最小值，Pimax为发电机i的有功出力的最大值。

把发电机的发电量作为约束条件后，为了协调网络的变化，需要把发电机的节点电压、变压器变比以及系统补偿作为约束条件，约束条件如下所示：

上式中：UGi为发电机i的电压值；Ti为变压器i的变比；QCi为无功补偿i的补偿容量；UGimin，UGimax，Timin，Timax，QCimin，QCimax为其变化范围的上下限。

为了满足系统运行的稳定运行，把发电机的无功出力和节点电压作为约束条件，约束条件如下所示：

式中：QGj为系统中发电机j的无功；Ui为系统中节点i的电压；QGjmin，QGjmax，Uimin，Uimax为其变化范围的上下限。

2.1.3 优化模型的建立

通过对以上的建模分析，可以得到优化串补配置的优化模型，模型如下所示：

2.2 基于随机权重粒子群算法优化模型

粒子群算法的开发是受到了鸟群搜捕食物的启发，当鸟类搜捕食物时，在食物周围区域的鸟群总是能吸引到其他搜寻食物的鸟类，然后在进一步搜捕食物的具体位置[9]。粒子的更新速度和更新位置如下所示。

上式中：为粒子的第k+1 次速度；为粒子第k次速度；c1，c2为学习因子；r1，r2为相互独立的伪随机数；Pid为个体最为优值；Pgd为群体最优值；为第k次粒子；为第k+1 次粒子。

为了使粒子群算法能够摆脱选取权重因子困难的局面，改善粒子的飞行速度，消除固定速度对寻优的限制，本文选取随机权重因子来克服这种不足，让权重随机但又能适应粒子群算法的速度更新。随机权重因子的公式如下：

式中：μmin为随机权重平均值的最小值；μmax为随机权重平均值的最大值；rand(0,1) 为0 到1 的随机数；σ为随机权重平均值的方差；N(0,1)为标准正态分布的随机数。

与遗传算法相比，粒子群算法有着记忆功能，能根据个体最优以及全局最优的轨迹进行搜寻调整自己的速度和位置，全局收敛能力要比遗传算法高。

基于随机权重粒子群算法优化串补配置首先对潮流计算的初始确定量进行初始粒子化。然后利用基于随机权重的粒子群算法进行寻优，如果潮流解不符合要求，则抛弃这组粒子。其优化模型流程如图2 所示。

图2 网络优化模型流程

3 算例仿真验证

本文以IEEE30 节点的输电系统进行仿真分析，模型如图3 所示。将网络串补位置、串补度、10 号与24 号节点的无功补偿和机端电压作为网络优化的参数，将变压器支路设为1。采用随机权重的粒子群算法进行优化求解，将网络模型控制参数设置为41 条线路支路都可以加入串补，串补数量设为6，串补度控制在0.1～0.8，9 号节点无功补偿容量范围为0～0.5，机端电压控制在0.95～1.05，发电机出力控制在0～0.8。粒子群算法种群规模200，进化次数200，速度更新中的参数为，c1=c2=1.49445，μmax=0.8，μmin=0.5，σ=0.2。

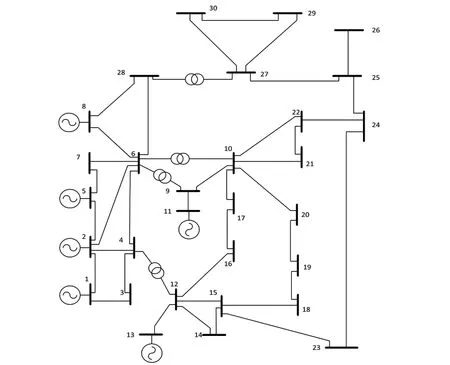
图3 IEEE30节点输电系统网络接线图

随机权重粒子群算法对模型进行优化，优化串补位置及配置，如表1 所示。

表1 IEEE30节点输电系统串补配置

潮流优化结果如下表2 所示。

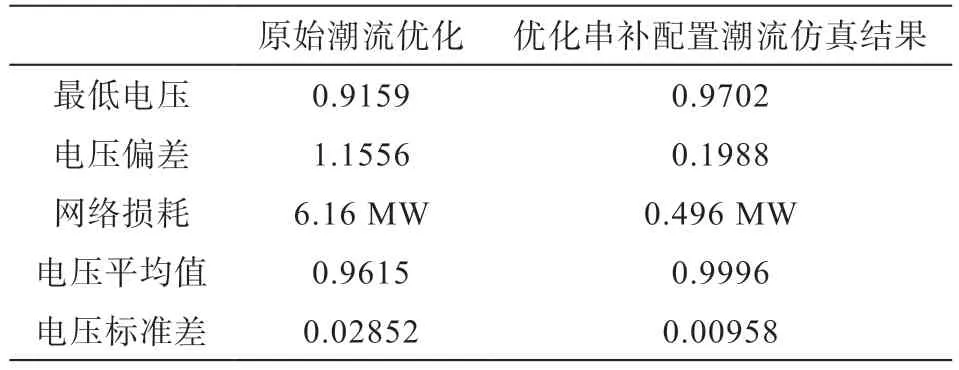
表2 IEEE30节点输电系统潮流结果对比

从表中可以看出，IEEE30 电力系统模型经过网络参数优化后，节点最低电压变高，网络电压偏差变小，网损升高；经过优化后，节点最低电压变高，网络电压偏差较原始网络减小，网损大大降低，电压平均值较网络优化值不变，电压标准差下降。由上述结果可以得出，考虑串补配置的机网协调优化对IEEE30 节点输电系统优化效果综合结果最好，验证了本文算法的有效性和合理性。