基于数据驱动的光伏电站理论功率计算方法

2023-11-11宋小龙刘友宽伍阳阳郭磊

云南电力技术 2023年5期

宋小龙，刘友宽，伍阳阳，郭磊

（云南电力试验研究院（集团）有限公司，云南昆明 650217）

0 前言

通常情况下光伏电站处于最大功率点跟踪运行模式（Maximum Power Point Tracking，MPPT），即通常说的自由发电模式[1]。当光伏电站投入AGC 闭环功能后，就必须根据AGC指令参与调节全站的有功出力，此时AGC 可控出力上限即为当前时刻的所有逆变器的理论功率之和[2]。而光伏逆变器的理论功率是实时变化的，与当前时刻的太阳辐照度、温度及总电阻等具有复杂的关系，在工程实践中难以应用[3,4]。本文考虑通过相关性的特征选择算法计算出特征相关性高的逆变器作为样板逆变器，然后分别使用线性回归和随机森林建立预测模型，最后以样板逆变器作为输入通过预测模型计算后的输出与实际自然发电的功率作比较，选出误差最小的计算方法。具体算法如图1 所示。

1 基于相关性的特征算法选择样本逆变器

Hall 于1999 年提出基于相关性的特征选择(Correlation-based feature selection，CFS)方法。CFS 方法是一种典型的filter 式特征选择方法，它启发式地将单一特征对应于每个分类的作用来进行评价，从而得出最终的特征子集[5]。

1.1 特征估计

CFS 估计特征子集，并对特征子集而不是单个特征进行排序，其核心是采用启发式的方式来评估特征子集的价值。CFS 通过计算特征之间的相关性以及特征与类标之间的相关性来实现特征的选择，其目的是使被选中的特征之间彼此尽可能不相关，而与类标之间高度相关。CFS 的启发式方程为：

式（1）中：merits表示包含k个特征的特征子集S 的merit（类别区分能力）；rcf 表示类别c 与特征f（f∈S）的平均相关系数；rff是特征f之间的平均相关系数；r为Pearson 相关系数，所有的变量需要标准化。分子部分表示特征子集S的类预测能力；分母部分表示特征子集S中特征的冗余程度。因此，分子越大表示特征子集S的类预测能力越强，分母越小表示该特征子集的冗余越小。

特征选择就是选择一组特征构成特征子集，该子集与类别高度相关，但是子集中的特征之间高度不相关。由此可见merits的值越大，当前特征子集S对于分类的贡献就越大，是优良的特征子集。

但在CFS 中，特征必须是离散的随机变量，而且是通过条件熵和互信息的计算方式来对特征之间和特征与类标之间进行评价，因此针对数据是连续性的随机变量时就难以处理。基于此，针对数据是连续性随机变量时可通过Pearson 相关系数来计算特征之间的相关性以及特征与类标之间的相关性。相关系数的绝对值越大，则相关性越强；相关系数越接近于0，则相关度越弱。

1.2 搜索特征子集空间

CFS（如图2 所示）首先从训练集中计算特征与类和特征与特征相关矩阵，然后用前向选择搜索策略（forward selection search strategy，FS）搜索特征子集空间，也可使用其他的搜索方法，包括最佳优先搜索（best first search，BFS）、后向消除（backward elimination，BE）。前向选择刚开始没有特征，然后贪心地增加一个特征，直到没有合适的特征加入。后向消除开始有全部特征，然后每一次贪心地去除一个特征，直到估计值不再降低。最佳优先搜索与其他两种搜索方法差不多，可以开始于空集或全集。以空集M为例，开始时没有特征选择，并产生了所有可能的单个特征；计算特征的估计值( 由merits值表示)，并选择merits值最大的一个特征进入M，然后选择第二个拥有最大的merits值的特征进入M。如果这两个特征的merits值小于原来的merits值，则去除这第二个最大的merits值的特征，然后在进行下一个。依次递归，找出使merits最大的特征组合。

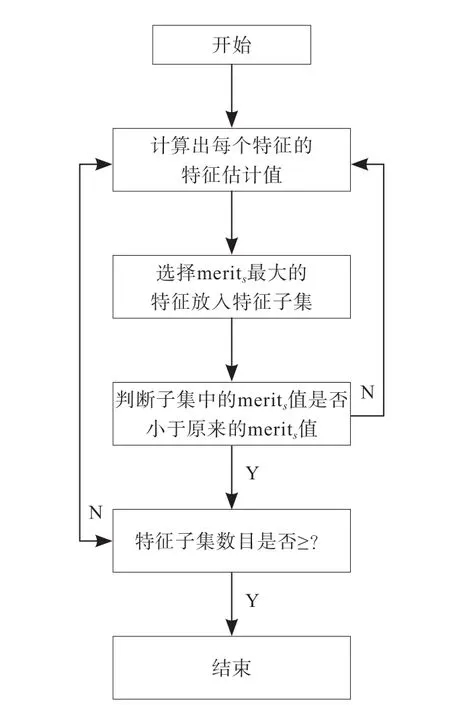
图2 CFS计算方法

图3 理论功率计算效果对比

2 AGC理论功率计算模型

在确定了样本逆变器的基础上，通过样本逆变器与训练集之间建立预测模型。由于训练集中的理论功率为自由发电状态下所有逆变器有功之和，其中也包含了样本逆变器，所以样本逆变器与理论功率呈强相关。在这种强相关性的关系下，本文选择了线性回归（LinearRegression，LR）和随机森林（RandomForest，RF）进行模型建立。

2.1 线性回归

线性回归主要涵盖两种不同的线性回归模型，即一元线性以及多元线性回归模型。通常来说，当仅仅只需要一个自变量x去进行预测工作时，一元线性回归模型由于较少的自变量x的数量，其模型复杂度将更为简单，同时也会由于忽略了关联度较高的自变量的使用而导致数据与模型拟合不足的问题[6]。因此，如何选择被使用自变量x的数量，以及如何选取关联度较高的自变量x去进行线性模型的搭建以及回归问题的解决是线性回归算法中的核心所在[7]。一元线性回归模型函数表达式如下所示：

式（2）中，为模型输出的预估值，而β0，β1为预测系数，可采用最小二乘法计算。

多元线性回归则使用多个关联自变量进行回归问题的解决方法，其模型函数表达式为：

与一元线性回归模型函数类似，m为所使用自变量x的总数，β0…βm则为各个自变量相对应的预测系数。

2.2 随机森林

随机森林（Random Forest，RF）是一种集成学习算法，是将多个弱分类器进行组合然后经过投票或求均值确定最后的结果。该算法由BREIMAN 提出，综合了其提出的Bagging算法和HO 提出的随机子空间方法，这可整体提高模型的精度和泛化能力。随机森林算法中的基本分类器是CART 决策树，又被称为分类回归树（Classification and Regression Tree，CART）[8]。

CART 算法是BREIMAN 和STONE 共同提出，该算法在信息熵的基础上并依据特定的准则构造得到的决策树。该算法与ID3 决策树算法和C4.5 决策树算法不同的是在节点分裂选择特征属性的时候采用了基尼指数（Gini Index）最小准则来进行选择，通过基尼指数可以选择特征属性并且通过基尼值可以反映样本的纯度。数据集D的纯度定义为：

式（4）中：pk为样本点属于第k类的概率；y表示数据集D的类别。

基尼指数定义为：

式（5）中：α为特征条件；υ表示数据集D中满足特征条件α的类别。

算法过程：

在原始样本数据集中进行k次Bootstrap 重采样，每次采集固定个数的样本且每采集一个样本都将样本放回，采样结束后即可得到k个子样本集。

利用CART 算法构建针对于每个子样本集的决策树。假设从第i个子样本集中选取出的特征fi中包含了C个类别，则其Gini值为：

式（6）中：pj为类别Cj出现的概率。

Gini值越小样本纯度越高。因此，决策树节点的分裂特征即为该决策树中所有特征Gini最小的特征。

每个子样本集按照步骤产生一颗决策树，所有样本子集的决策树共同构成随机森林。每棵决策树在生长时，随机从含有M个特征的特征集合T中抽取个特征作为一个特征子集，将抽取出的特征子集作为决策树的划分属性，按照Gini值最小准则生长决策树。

利用多数投票算法对所有决策树的结果进行分析和投票，最终的投票结果即为随机森林的结果。

3 实例分析

本文选择某总装机30 MW 光伏电站作为实例。该光伏电站共有60 台同规格型号的单台容量为0.5 MW 的逆变器，编号为#1～#60。采集的数据为自由发电运行中的2022 年6 月1 日至11 月24 日每台逆变器开始上网到下网的实发有功值及总的有功值，其中若某台逆变器发生故障、通讯中断等情况，这也是一种特征，在这里将其实发有功值置为0 处理。另外将每月1至5 日五天的数据作为测试集，其余数据作为训练集。