航天试验数据时间序列相似度分析
2023-11-11夏心蕾刘俊阳彭汉章韩翔宇
夏心蕾,刘俊阳,彭汉章,韩翔宇
北京航天自动控制研究所,北京 100854
0 引言
在航天、电信、医疗等多个领域中,曲线类型数据都有着广泛应用。如何挖掘曲线类型数据是一项重要研究内容。在航天领域,飞行器的各种数据是判断飞行器状态是否正常的一项重要依据。曲线数据的正确性判断通常需要专业人员快速给出结论,因而不仅对专业水平要求较高,也存在一定的人为误判、漏判风险,所以自动判读曲线数据正确性对提高航天试验的判读效率具有重要意义。
时间序列判读方法主要分为基于统计特征的判读方法[1-2]、基于相似度度量的判读方法[3-4]和人工智能判读方法[5-6]。基于统计特征的判读方法通过构建数据的统计分布模型,检测时间序列异常。该方法难点在于数据分布特性的识别与描述[1]。基于相似度的判读方法通过计算序列间的距离检测异常。常用的相似度度量方法有欧氏距离、弗雷歇距离、DTW(Dynamic Time Warping)距离等。欧式距离是最常用的计算距离的方法,计算方法简单、时间成本较低,但无法处理长度不同的时间序列。弗雷歇距离和DTW距离均可对长度不同的时间序列进行处理,弗雷歇距离求解的是两个时间序列的最大距离而DTW距离求解的是累积距离。文献[3]对马氏距离、DTW距离、夹角距离等多种相似性度量方法在卫星遥测数据异常检测中的效果展开研究,验证了基于DTW距离的异常检测方法效果较好,能够识别差异较小的异常序列。文献[4]提出先使用SAX降低序列长度,再使用Fast-DTW进行卫星异常检测。但这些研究中没有将周期数据和非周期数据进行区分处理,当检测周期数据时,无法识别出周期信号的幅度这个重要特征的正确性,尚不能完全满足周期信号的判读要求。人工智能判读方法的典型算法包括最近邻、支持向量机、神经网络等。这类算法需要对每种类型曲线进行训练,对于繁多的曲线类型,工作量巨大,并且无法完全保证被测数据集分析结果的准确性,因此在安全关键领域应用难度较大[5],应用广度受到限制。
由于某航天试验数据中周期和非周期曲线的判读方法不同,仅采用同一种相似度度量方法,会带来较大判读偏差,因此需要首先对周期曲线和非周期曲线进行分类。文献[4]采用基于极值的分段方法对伪周期时间序列进行分割。文献[7-8]提出基于趋势的符号化表示(TSX)分割方法,从而支持相似搜索。但上述这些研究是针对伪周期时间序列的周期估计,并不能很好地识别非周期曲线。
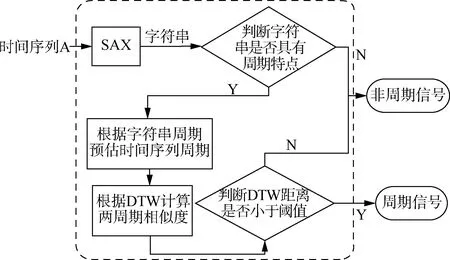
本文首先说明曲线数据的周期性检测方法,再针对周期和非周期两类曲线分别构建相似度分析方法,通过分析与模板序列的相似度,预估曲线的正确性,其流程如图1所示。本文使用符号近似方法SAX和DTW距离计算相融合的方法用于周期性检测,对周期和非周期数据进行分类;使用带有双维度约束的DTW距离计算方法计算非周期信号相似度,使用与无约束DTW距离对比的方法判别曲线是否相似;最后提出了曲线模板更新方法,自动生成标准曲线。

图1 曲线数据的相似度分析流程
1 符号化表示与DTW距离
1.1 符号化表示
符号集合近似(SAX)是一种将时间序列离散化为字符串的方法。该方法首先假设时间序列服从正态分布,通过等分正态分布(用字母表示)划分时间序列值空间,将落在对应分布空间的均值映射为对应的字母。算法思路分为2步:1)标准化转换并利用分段聚合近似(PAA)进行数据降维;2)将PAA的结果用字符串表示。
标准化曲线数据使其均值变为0、标准差变为1。假设时间序列A=[a1,a2,…,an],标准化后为A′,需要将其转换为长度为w的字符串S=[s1,s2,…,sw]。PAA算法首先将A′切分为w个片段,每个片段采用取均值的方法求解,即将A′转换为B=[b1,b2,…,bw]。
(1)
根据正态分布生成α个字符组成的字符集,每个字符对应一个一维区间,每个区间对应的正态分布概率相等。将PAA降维后的序列B中的每一个片段映射到字符区间上,从而转换成字符串表示。
符号空间距离度量方法认为相同字符的距离为0,不同字符的距离等于所对应区间较大的字符对应的区间下界减去所对应区间较小的字符对应的区间上界。
1.2 DTW距离
DTW计算距离的主要思路为弯曲时间轴,通过寻找两条时间序列的最佳对应关系,获得最小累积距离。
时间序列A=[a1,a2,…,an],时间序列B=[b1,b2,…,bm],令矩阵Mb记录基距离,即Mb(i,j)表示ai和bj的基距离,度量方式可采用曼哈顿距离。若Mb中路径W=[w1,w2,…,wK]满足:1)max(m,n)≤K≤m+n-1;2)W起始于w1=(0,0),终止于wK=(n,m);3)对于wi,1≤i≤K-1,令wi=(xi,yi),wi+1=(xi+1,yi+1),若0≤xi+1-xi≤1,0≤yi+1-yi≤1,则称路径W为弯曲路径。DTW算法的任务是在所有弯曲路径中找一条累积距离最小的路径,DTW距离是这条最小路径的累积距离,计算方法如下:
(2)
实现中使用动态规划对DTW距离进行求解。定义矩阵Md来表示时间序列A和B的最小累积距离,假设Md的i行j列元素的值为γi,j:
(3)
γi,j=Mb(i,j)+min{γi-1,j,γi,j-1,γi-1,j-1}
(4)
dDTW(A,B)=γn,m
(5)
其中:i和j的取值范围分别为0 DTW算法主要存在两个问题:算法时间复杂度较高,处理大规模时间序列的相似度计算速度较慢;算法存在奇异值点,即时间序列A中多个点与时间序列B中的同一个点对齐,这将导致虽然两条时间序列差异较大,但计算出的DTW距离却很小。在DTW算法中加入全局约束的方法可以避免奇异值点问题,降低算法时间复杂度。 周期性检测可以通过SAX方法,将时间序列转换为字符串,通过字符串的周期性间接判断时间序列的周期性,但由于SAX中采用了PAA方法对数据降维,损失了时间序列的精度,因此这种判断方法精度较低,存在误将非周期时间序列判断为周期时间序列的可能。周期性检测还可以通过DTW方法判断时间序列各段周期是否相似,从而判断曲线周期性。但由于时间序列的周期未知,需要逐个值代入测试,而周期可能的取值范围大,导致该方法时间复杂度高。综合考虑上述情况,本文提出双重周期性检测方法,结构图如图2所示。第1步周期性检测采用SAX方法,对字符串的周期性进行检测,从而初步排除非周期曲线并预估出周期; 第2步检测实际上是在第1步检测结果的基础上再进一步进行周期性确认,即使用第1步检测预估的周期,采用DTW方法测量每两个相邻周期时间序列的相似性。只有两步检测结果都为有周期性的时间序列才被确认为周期信号。 图2 双重周期性检测结构图 字符串周期预测计算的主要思路为先将原字符串进行不同长度lshift的循环移位,分别计算移位后的字符串与原字符串的距离dstr(无量纲);然后根据所记录的不同移位长度对应的距离,判断是否存在T,使得距离在移位长度为c×T,(c=1,2,…)时循环达到极小值,曲线周期性震荡。若存在,则预测T为字符串周期。周期曲线满足上述规律,如图3(a);非周期曲线无此规律,如图3(b)。极小值判断设定阈值θxtrm,当该点小于其前后点的值,并且差值大于θxtrm时,认为该点为极小值点。 图3 字符串不同移位长度对应的距离 通过DTW距离测量某一时间序列每两个相邻周期的相似度,通过周期间的相似度进一步确认该时间序列是否具有周期性。将字符串周期预测得到的字符串周期与每个字符代表的时间序列长度相乘,得到时间序列预测周期。设时间序列预测周期为Tts,则 (6) 将时间序列向前移动一个预测周期的长度,则向前移动后的时间序列长度为lts-Tts。将向前移动后的时间序列和原序列前lts-Tts长度的序列进行比较,使用DTW距离度量两者的相似度。只有当该距离小于设定阈值,认为该时间序列为周期序列。 在上述周期性分析中对序列进行了降维,因此得出的预测周期,往往不是原时间序列的真实周期,可能为真实周期倍数。周期曲线的真实周期值需要通过离散傅立叶变换(DFT)对其频域特征值进行分析获得。此外,根据某航天试验数据要求,周期曲线判读标准为待测数据曲线的幅度与理论幅度相差不大于Δ。本文通过对判读结果为正确的数据序列集的幅度取均值,动态生成幅度模板,将待测曲线幅频特征与模板幅频特征进行比较,通过两者的一致性来初步判断周期曲线的正确性。在对曲线相频特性有分析要求时,则需要进一步分析判断。 除了通过频域特征分析周期曲线外,还可以增加对曲线形状的分析,通过记录曲线单个周期数据,生成单周期模板,比较模板与待测曲线的形状相似性,进一步精确判断周期信号的正确性。 对于非周期的航天试验数据曲线,允许同一工况下不同的试验过程之间的测试值在时间序列上伸缩对齐,也就是允许一定程度上时间序列回卷后相似,这种特性的数据适合使用DTW距离进行分析。但由于某航天试验数据判读对测试值在时间以及幅值上的偏移距离均有限制,因此需要在DTW距离算法的基础上分别加入时间和幅值偏移约束,形成带双维度约束的DTW距离计算方法,来满足本领域曲线的相似性评价标准。 时间约束使用S-C全局约束方法。设置时间约束值rt,rt为1的S-C全局约束方法如图4。阴影部分表示弯曲窗口,限制得到的最小累积距离弯曲路径在这个弯曲窗口内。 图4 S-C全局约束方法 在S-C约束下,加入对幅值的约束。假设A为模板序列,B为待测序列。设置数据点bi的上下界,根据S-C全局约束方法,序列A中只有数据点集{ai-rt,ai-rt+1,…,ai+rt}可与序列B的第i个数据点bi对齐,以数据点集的最大值作为上界,最小值作为下界。同时,加入幅值约束松紧度θtyt,动态调整幅值约束的松紧度。若满足式(7),则认为bi满足幅值约束。 在用动态规划算法计算双维度约束的DTW距离时,定义矩阵Mdual表示双维度约束下的最小累积距离矩阵,如式(8)。 通过全局约束限制最小累积距离弯曲路径的偏移量,可以避免奇异值问题,时间复杂度可以降为O(n)。 (7) (8) 由于非周期时间序列分析需要模板曲线,本文根据计算DTW距离时得出的最小弯曲路径,动态更新标准曲线。当该待测曲线相似度分析结果为相似时更新模板。假设旧模板中第i个点为oi,在最小弯曲路径中检测曲线A与oi对齐的所有点的均值为aavg,则新模板中第i个点ui的表达式为: (9) 式中:n为更新模板的次数。 为验证本文所提方法的正确性,使用某运载项目航天试验数据进行了实验分析,待测曲线示例如图5所示。下面对3种典型曲线进行分析。 图5 某航天试验曲线数据示例 对于周期曲线,以曲线1为例,前51个数据点的SAX转换过程如图6。虚线表示通过等分正态分布划分值空间,由下往上,每个值区间分别对应字母a至h,前51个数据点转换生成字符串“adgccffbehadgccff”。 图6 SAX转换示意图(曲线1) 对转换后的字符串进行周期检测,极小值点判断阈值设置为0.5。图7为不同循环移位长度对应的字符串距离,圆圈标注出了距离极小值点,其中实心圆表示周期最小的周期性出现的极小值点,两个相邻实心圆的距离即为预估周期。字符串周期检测结果为10,则预估时间序列的周期为30。 图7 字符串周期预测示意图(曲线1) 周期时间序列DTW相似度计算设定阈值为0.1,曲线1的DTW距离为0.0408,小于设定阈值,周期性检测结果为周期曲线。通过离散傅里叶变化计算得出时间序列周期为10,与预期相符。 对于非周期曲线,以曲线2为例,截取前51个数据点的SAX转换过程如图8。转换生成的字符串为“dddddhhhhhhhhhfdd”。对转换后的字符串进行周期检测,不同移位长度对应的字符串距离如图9,由于没有满足周期性出现特征条件的极小值点,检测结果为非周期序列,符合预期。 图8 SAX转换示意图(曲线2) 图9 字符串周期预测示意图(曲线2) 以曲线2为例,如图5(b),将曲线2的第400点加入幅值为1的脉冲扰动,构造得到加扰曲线,不同约束DTW度量方法测量出的被测曲线和模板曲线的距离如表1,其中S-C约束与双维度约束的时间约束值均为1,双维度约束的幅值约束松紧度设置为0.2(θtyt=0.2)。加扰曲线的无约束DTW距离和带有S-C约束的DTW距离都可能小于正常曲线累积距离阈值,即存在部分曲线相似度分析结果与实际不符的可能。而双维度约束DTW距离算法的计算结果因为有幅值约束,因此结果为无穷大,从而识别出曲线异常。 表1 曲线2不同约束DTW度量方法结果 以曲线3为例,如图5(c),将曲线左移3个单位构造得到异常曲线数据。采用不同约束DTW度量方法测量出的上述两条曲线与模板曲线的距离如表2。本试验原曲线的双维度约束和无约束DTW距离的比值为5.19,小于θcmlt(本实验中设定为10);异常曲线的双维度约束和无约束DTW距离的比值为13.02,大于θcmlt,偏差显著。因此,采用本文双维度约束和无约束DTW距离比较的距离分析方法,可以在一定条件下较为有效地识别由于时间弯曲过大带来累积距离的异常。 表2 曲线3不同约束DTW度量方法结果 下面对3种约束DTW度量方法进行耗时统计,如表3,双维度约束方法计算时长明显小于无约束方法。对于正常曲线,由于双维度约束中加入了幅值约束的判断,因此其计算时长略大于S-C约束方法的计算时长。对于异常曲线,双维度约束计算时长小于S-C约束方法的计算时长。显然,双维度约束算法与S-C约束相当,比无约束快约一百倍。 表3 不同约束DTW度量方法耗时 本文针对某航天数据的时间序列判读的难点问题,提出了SAX和DTW融合的双重周期性检测方法和带有双维度约束的DTW非周期相似度计算方法。在某航天试验数据集上进行分析实验验证,结果表明本文提出的分析方法正确有效。2 周期性曲线综合检测和分析
2.1 方法概述
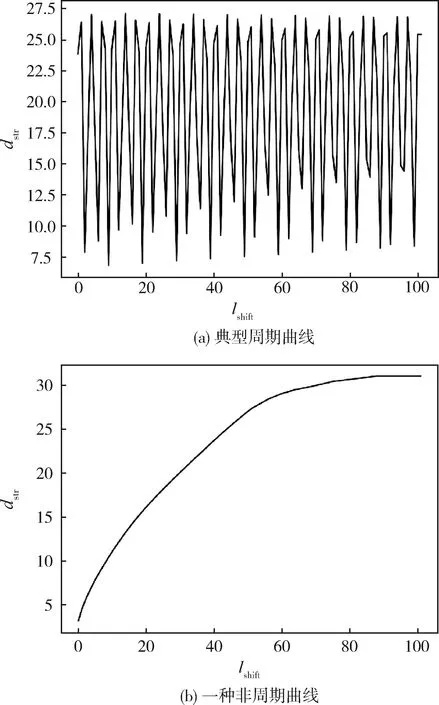
2.2 字符串周期性预测方法
2.3 时间序列的周期相似度分析
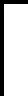
2.4 周期曲线的频域特征值计算
3 非周期曲线分析方法
3.1 双维度约束的DTW距离

3.2 距离分析方法
3.3 非周期时间序列模板生成
4 实验验证
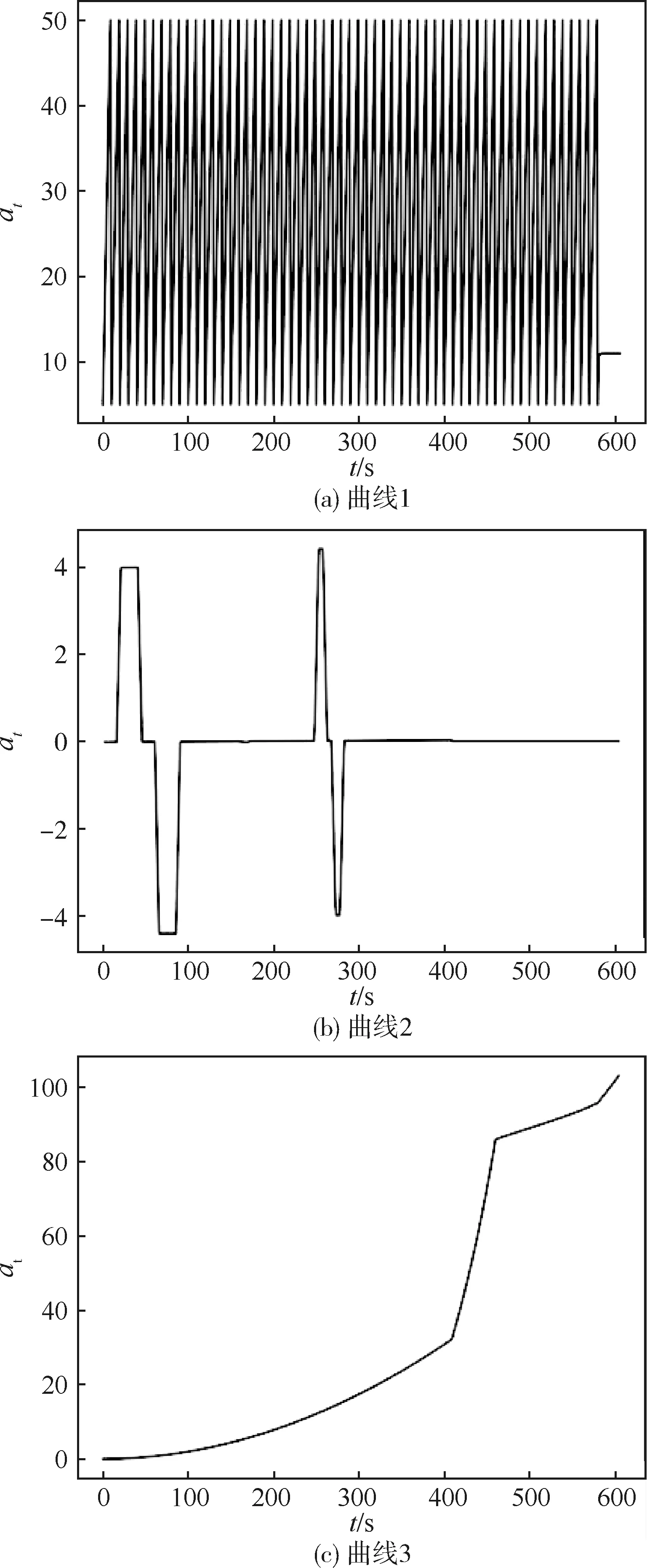
4.1 周期性的检测和分析


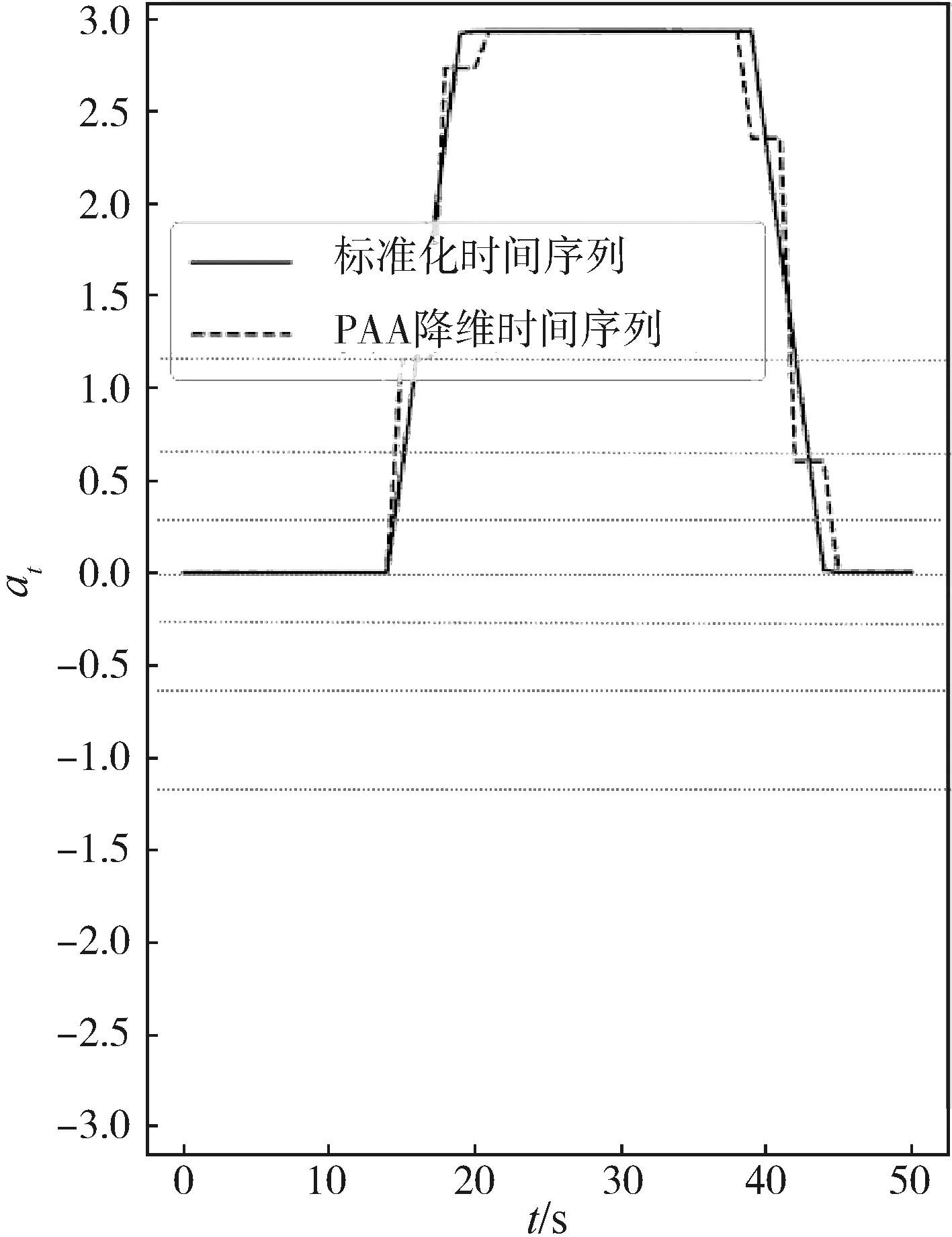
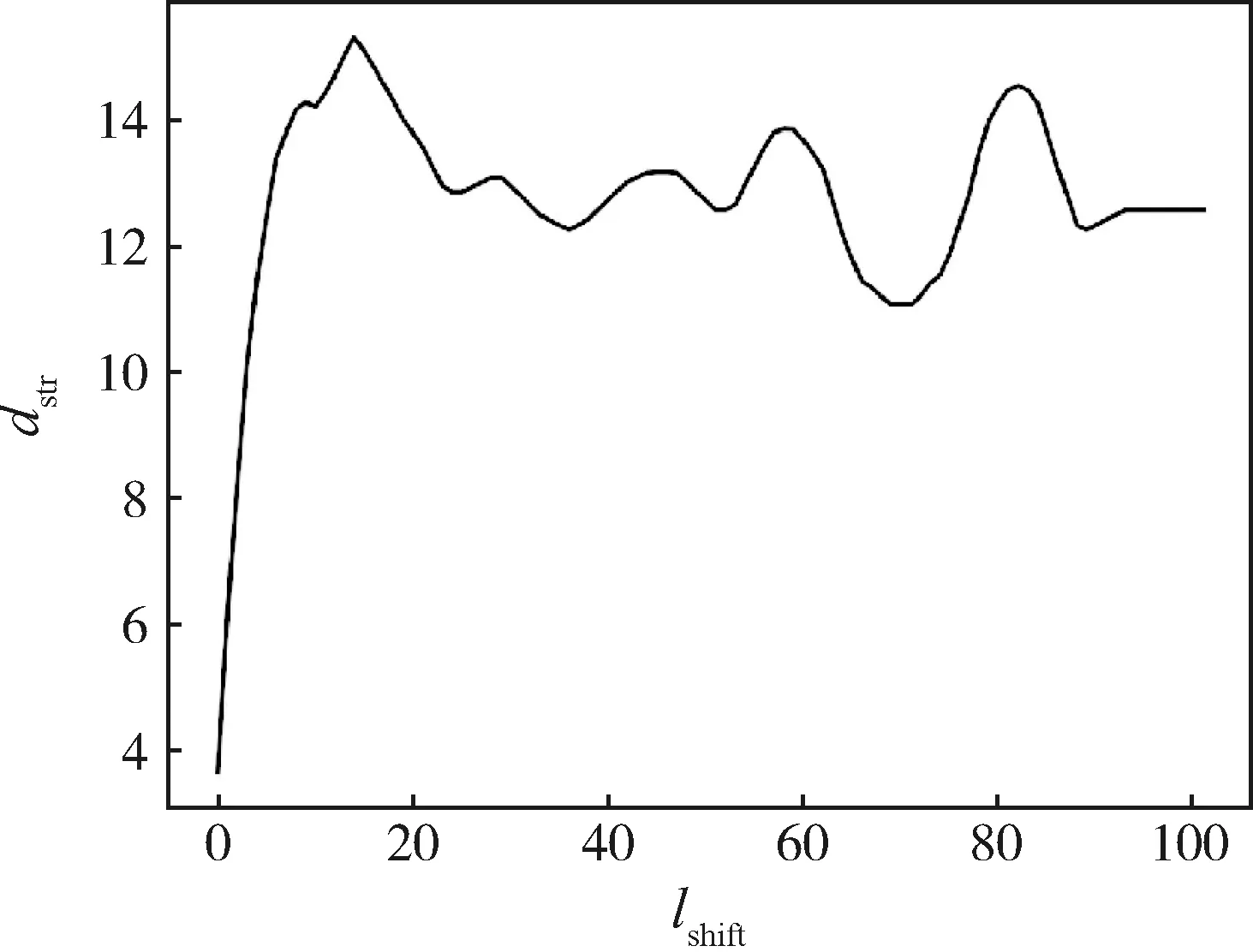
4.2 非周期曲线相似度分析



5 结论
