一种磁悬浮飞轮特定参数摄动鲁棒控制方法*

张 立, 向彦霖

国防科技大学空天科学学院,长沙 410073

0 引言

磁悬浮飞轮控制器算法的精度、复杂度和实时性通常会相互掣肘,转子转速较高时控制器必须提高刷新频率以避免过大的相移,控制周期缩短导致无法完成过于复杂的控制策略,故PID控制器(Proportional-Integral-Derivative Controller,PID Controller)成为工程实践中主要采用的控制策略。

PID控制器的参数整定没有从顶层设计上考虑鲁棒性,模型参数摄动情况下控制性能的变化难以预测,工程上通常用试错法回避此类问题。鲁棒控制理论设计控制器时,如果假设的摄动参数比较多,所得到的鲁棒控制器就比较保守,只能以降低时域性能为代价来提高鲁棒性。

实践中发现磁悬浮飞轮控制对象模型各参数中,位移刚度参数摄动的概率和幅度都最大,且该参数摄动对闭环控制系统的性能影响也最大,为了充分利用这一已知信息,可以采用参数化特征值配置技术(Eigenvalve Assignment, EA)[1],用闭环系统特征值对位移参数的灵敏度作为性能指标,通过求解指标函数的极值来计算特征值并推算全状态反馈控制参数。

在磁悬浮飞轮上实现全状态反馈控制通常需要状态观测器,这会导致控制器计算量的大幅增加,不利于高速状态下的实时控制。对于这一问题,可以通过设计由控制对象输入输出信息直接推算出的状态变量,构造非最少状态空间控制(Non-Minimal State Space control, NMSS control)模型[2]来实现无状态观测器的全状态反馈控制。

NMSS控制结合了PID控制简单易实现和状态空间控制全息、参数整定理论完备的优点,也被称为比例积分加控制[3](proportional-Integral-Plus control,PIP control)。NMSS状态向量中含有输入输出信号的微分平坦项和积分项,闭环控制系统抗干扰性能优于未增广状态的最少状态空间控制系统[3]。

对于控制时滞、功放非线性等其他非理想因素导致的控制性能下降,可以采用等价干扰信号补偿控制方法(Equivalent Disturbance Compensation, EDC)[4]将这些因素等价为控制器输出误差分量,通过构造逼近该分量的补偿信号来抵消未建模误差对控制系统的影响,由于补偿信号及其滤波器所引入的系统特征值远离原系统主导特征值[5],该方法可以在不影响其他控制器实现、也不影响系统主导特征值下获得较好的干扰抑制效果,且算法运算量比较低,易于航天应用[6]。

本文将非最少状态空间控制与参数化特征值配置、信号补偿技术结合起来应用于磁悬浮飞轮控制(下面称其为NMSS-EA-EDC方法),其中前两种技术的组合已在倒立摆实验平台上验证了可行性和有效性[7]。

1 磁悬浮飞轮模型及能控性

1.1 物理模型及最少状态空间模型

磁悬浮飞轮转子运动方程(在平衡点附近线性化之后)如下:

(1)

其中:kx和ki为等效位移刚度和电流刚度,f为转子受到的电磁力之外的其他扰动力,m为等效单通道转子质量,x和i分别为转子位移和磁轴承电流。以电流为输入、转子位移为输出的传递函数模型为:

(2)

(3)

(4)

(5)

将最少状态空间模型状态矩阵和输入矩阵中含摄动参数的元素定义为a21=kx/m,b2=ki/m。

1.2 非最少状态空间控制模型

选择状态向量xnm如下:

(6)

其中:s代表拉普拉斯算子,z=-x/s代表转子位移偏差的积分,T(s)=s2+t1s+t2为滤波多项式,t2≠0。则非最少状态空间模型为:

(7)

其中,状态矩阵、输入矩阵和输出矩阵分别为:

(8)

h=[a21+t2t1b20 0]

(9)

1.3 模型能控性

定理1.非最少状态空间模型(7)能控的充分必要条件是1.1节中物理模型所对应的最少状态空间模型(3)能控。

证.根据PBH(Popov, Belevitch and Hautus)判据,模型(7)能控等价于对任意复数λ,P(λ)=[λI-F,g]的秩为5。

必要性:若模型(3)不可控,则P(λ)前2行的秩小于2,模型(7)不可控。

充分性:若模型(3)可控,则P(λ)前2行的秩为2,且b2≠0。由后者可得P(λ)后3行的秩为3,则模型(7)能控。

2 优化对特定参数摄动的适应性

非最少状态空间闭环控制系统模型框图为:

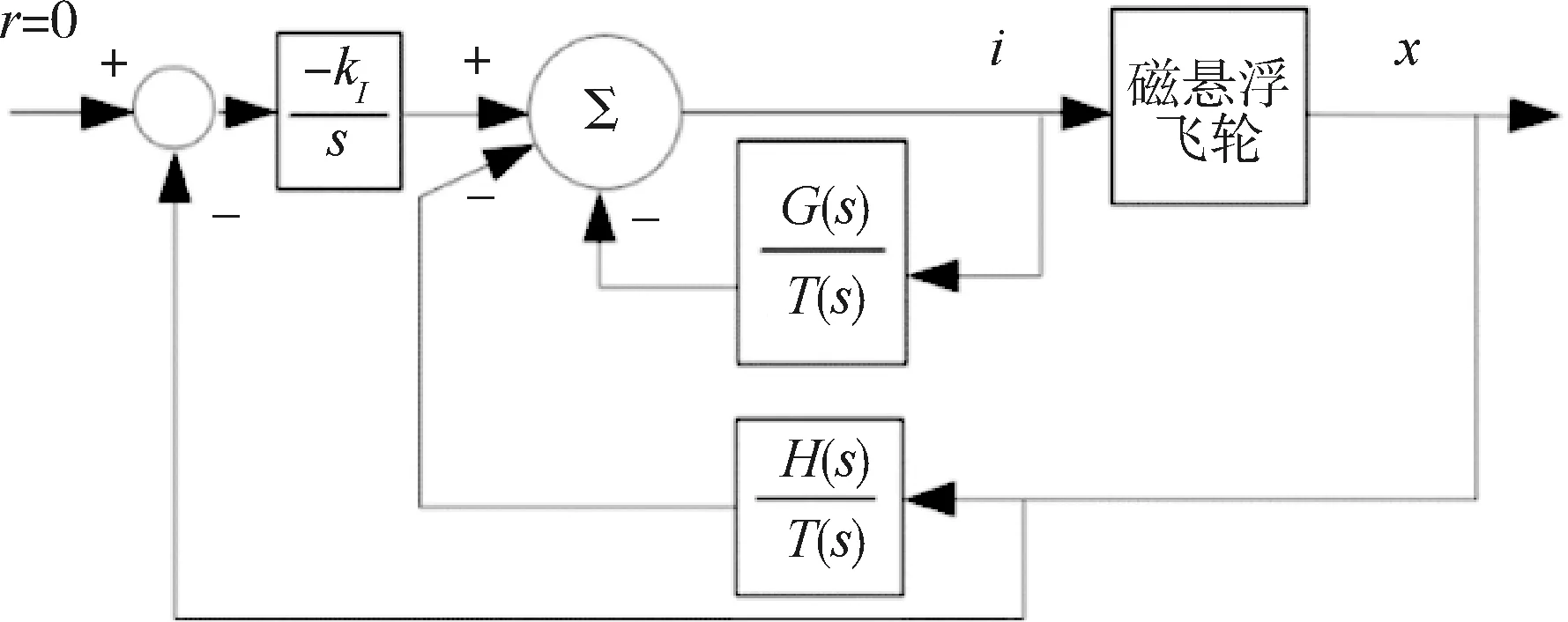
图1 非最少状态空间闭环控制系统模型框图

其中:多项式G(s)和H(s)定义为:

G(s)=k3+k4s

(10)

H(s)=k1+k2s

(11)

其中:k1～k4为状态反馈控制器k中的参数。

k=[k1k2k3k4kI]

(12)

闭环控制模型的状态矩阵为Anc=F-gk,为了提高鲁棒性,设定约束Anc为正规矩阵(无重复特征值)。用闭环状态矩阵Anc的特征值对特定摄动参数kx的灵敏度值来构造优化指标函数。根据Hellman-Feynman定理,对于正规矩阵,其特征根灵敏度函数求法为:

(13)

其中:ti和vi分别为第i个特征根对应的左、右特征向量。可根据工程实际需求决定是否在指标函数中加入扰动敏感度项和控制能量代价项[1]。根据系统时域性能指标约束,在s平面上画出等超调量线、等调节时间线等性能边界,在边界内求指标函数最优解得到闭环系统最佳特征根,在无重根约束下可以通过极点配置法唯一求解控制器中的5个参数。

3 参数摄动等价干扰信号补偿

控制对象传递函数模型式(2)可以写成:

y(s)(s2-kx/m)=(ki/m)u(s)

(14)

引入等价干扰控制量v(s),把上节控制器计算输出的理论控制量u(s)写成两部分的和:

(15)

(16)

为了使上式等号右边传递函数可以物理实现,引入二阶低通滤波器φ(s):

(17)

用φ(s)v(s)逼近等价干扰控制量v(s),得到信号补偿后系统真实控制量:

(18)

上式即为磁悬浮飞轮等价干扰信号补偿控制算法。

4 数值仿真

将NMSS-EA-EDC控制策略应用于文献[1]中磁悬浮飞轮的一个垂直通道,系统参数见表1。将闭环系统特征根中的4个设定为-50, -60, -70, -80,主导特征根通过多目标优化策略求解。设定标称时域性能指标为调节时间小于1 s,超调量不超过5%,则主导特征根寻优范围选为s平面负实轴上实部小于-4的部分。图2给出主导特征值为-8时转子位移阶跃响应参数摄动蒙特卡洛仿真结果。其中,位移刚度kx的最大摄动幅度为标称值的万分之五。

表1 磁悬浮飞轮参数

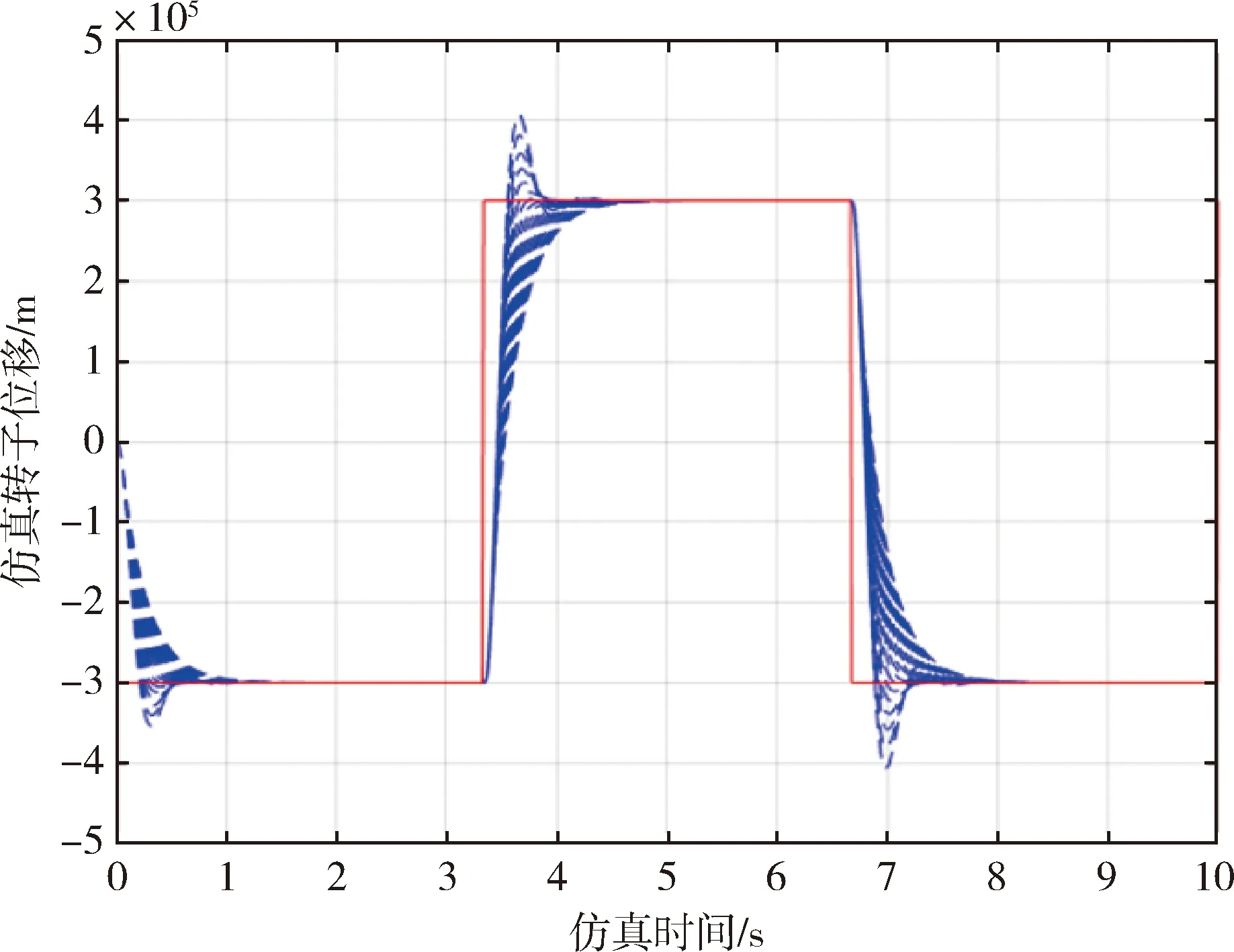
图2 仿真结果(NMSS-EA方法,参数摄动0.05%)

采用文献[6]信号补偿方法后再次进行相同设定的蒙特卡洛仿真,结果如图3所示。对比图2和3可以看出,信号补偿方法在相同的闭环特征值下显著降低系统对位移刚度参数摄动的敏感度。

图3 仿真结果(NMSS-EA-EDC方法,参数摄动0.05%)

进一步研究NMSS-EA-EDC闭环控制系统的特征值对参数摄动鲁棒性能的影响,将闭环系统特征根设定为-363.6, -374.5, -680, -790, -1905。主导特征值为-363.6时NMSS-EA-EDC方法阶跃响应参数摄动蒙特卡洛仿真结果如图4所示,当闭环系统的特征值离虚轴很远时,NMSS-EA-EDC方法在参数摄动70%的情况下仍然能够正常工作,但此时系统超调量较大,这表明过于保守的特征值配置虽然鲁棒性强,但牺牲了一定的时域性能。

图4 仿真结果(参数摄动70%)

5 结论

将NMSS、EA、EDC三种方法结合起来应用于磁悬浮飞轮的转子悬浮位移控制,通过数值仿真进行了控制算法验证研究,可得出:位移刚度等系统关键参数的摄动对磁悬浮飞轮控制系统时域性能影响很大;可以用主导特征值对摄动参数的灵敏度函数来有效表征系统对参数不确定性的容忍度;闭环系统最靠近虚轴的主导特征值离虚轴越远控制器对参数摄动的适应性越好,但控制所需能量代价越大;可以通过设计包含主导特征值对摄动参数的灵敏度、系统控制能量代价函数、系统对外界干扰的灵敏度的指标函数来实现磁悬浮飞轮多目标优化控制。

为了实现无需状态观测器的全状态反馈控制策略,可以将控制模型增广为非最少状态空间模型,状态变量中各元素可由控制对象的输入、输出量计算得到,能够在充分利用系统有用信息的前提下有效降低多目标优化控制器设计问题的复杂度。此外,增广状态带来更多可调特征值,在相同的主导特征值条件下,在调节时间等时域性能上有更大的回旋余地。

信号补偿方法可以在不改变主导特征值的前提下显著提高控制器对参数摄动的适应性。当位移刚度参数摄动达到标称值的70%时,NMSS-EA-EDC方法仍然能够镇定系统。