不平衡电网下变流器多机系统的稳定性分析
2023-11-11邹志翔杨佳俊GiampaoloButicchi
张 益,邹志翔,杨佳俊,陈 武,王 政,Giampaolo Buticchi,程 明
(1.东南大学 电气工程学院,江苏 南京 210096;2.宁波诺丁汉大学 理工学院,浙江 宁波 315100)
0 引言
在可再生能源的并网技术和灵活输电系统中,电压源型变流器(voltage source converter,VSC)已经被广泛应用且数量日益增加,如各类风电场、分布式光伏等[1]。电网阻抗受输电线路、变压器漏感等因素的影响表现出时变特性。同时,不对称故障的发生和大量不平衡负载的接入造成公共耦合点(point of common coupling,PCC)的电压和阻抗出现不同程度的不平衡现象[2-3]。随着可再生能源发电渗透率迅速地增加,电网在运行过程中频繁出现由变换器控制与电网阻抗相互作用导致的低频谐波稳定性问题[4-5]。因此,分析评估VSC 在不平衡电网条件下的稳定性问题具有重要的现实意义。
阻抗建模是开展系统稳定性分析的有效工具之一[6-7]。基于三相平衡电网的dq阻抗模型[8-11]、序阻抗模型[12-15]以及复频域模型[16-18]已经被广泛应用于新型电力系统的稳定性分析与设计。三相平衡电网系统在dq坐标系下呈现线性时不变(linear timeinvariant,LTI)特性,然而当系统是线性时间周期(linear time-periodic,LTP)变化时(如一些三相不对称系统),上述文献中的建模方法将不再适用。
三相不平衡电网下的阻抗建模近年来引起了广泛关注[19-22]。文献[19]使用谐波传递函数(harmonic transfer function,HTF)建立了基于不平衡电网的VSC 序阻抗模型,将序阻抗建模方法拓展至三相不平衡范畴,并解释了三相不平衡电网下频率之间的耦合关系。文献[19]建立的VSC阻抗模型仅考虑了同步参考系锁相环(synchronous reference framephase locked loop,SRF-PLL)。不过在不平衡电网中SRF-PLL 对100 Hz 电压分量的削弱能力是有限的。文献[20]考虑了不平衡电网下锁相环(phase locked loop,PLL)的耦合作用,利用复频域模型建立了VSC的广义多频导纳模型。文献[20]还分析对比了采用陷波滤波锁相环(notch filter-PLL, NF-PLL)与SRF-PLL 的动态响应,进一步完善了不平衡电网下VSC的频率耦合现象。文献[21]建立了不平衡电网下双解耦同步参考系锁相环(decoupled double SRF-PLL,DDSRF-PLL)的模型,详细分析了PLL 中频率耦合现象的产生过程,以及负序电压大小对频率耦合现象的影响。文献[22]提出采用二阶复数滤波器结构PLL 的控制策略,用于抑制直流偏置产生的频率耦合影响。不平衡电网下广泛使用的双二阶广义积分器锁相环(double second-order generalized integrator-PLL,DSOGI-PLL)模型及其VSC 系统的相关稳定性分析并未见有研究报道。
考虑不同类型PLL配置的多VSC 系统稳定性分析对新能源电厂有着更强的工程参考价值。目前,三相平衡电网下多机系统的稳定性问题已经得到了较好的研究[9]。在文献[19-22]中,研究人员主要研究了三相不平衡电网下单VSC 的建模和稳定性评估,然而对多VSC 与电网阻抗之间的相互作用没有给予重视。
因此,本文选取不平衡电网下带不同PLL 的多VSC 系统开展稳定性研究。首先建立了三相不平衡电网条件下VSC 的输出导纳模型。在此基础上,研究并分析了带不同类型PLL的VSC的频率耦合特性以及负序电压对VSC 输出导纳特性的影响。进一步,针对多VSC系统的稳定性问题、关键环节之间的作用机理以及多VSC系统中PCC处负序电压大小对系统稳定性的影响进行了研究。最后,通过仿真和实验验证了理论分析的准确性。
1 多VSC系统介绍
图1 为多个VSC 并联的典型拓扑结构。每一个VSC 都有一个LCL 型滤波器和一个控制系统单元。图中:Lf1x和Lf2x(x=1,2,…,n)为对应变流器的滤波电感;Cfx为滤波电容;Rx为滤波电阻;Vdcx为直流输入电压;icyx(y=a,b,c)为VSCx注入电网的三相电流;Zgy为三相电网等效阻抗,可以取不同值;Vg为电网电压。在电网运行过程中,三相电网阻抗和三相电网电压均可能存在不同程度的不平衡,造成并网交互系统稳态工作点的改变,进而带来并网交互系统的稳定问题。本文通过改变Zga、Zgb和Zgc的大小,并注入基频负序电压来构造三相电网电压的不平衡状态。
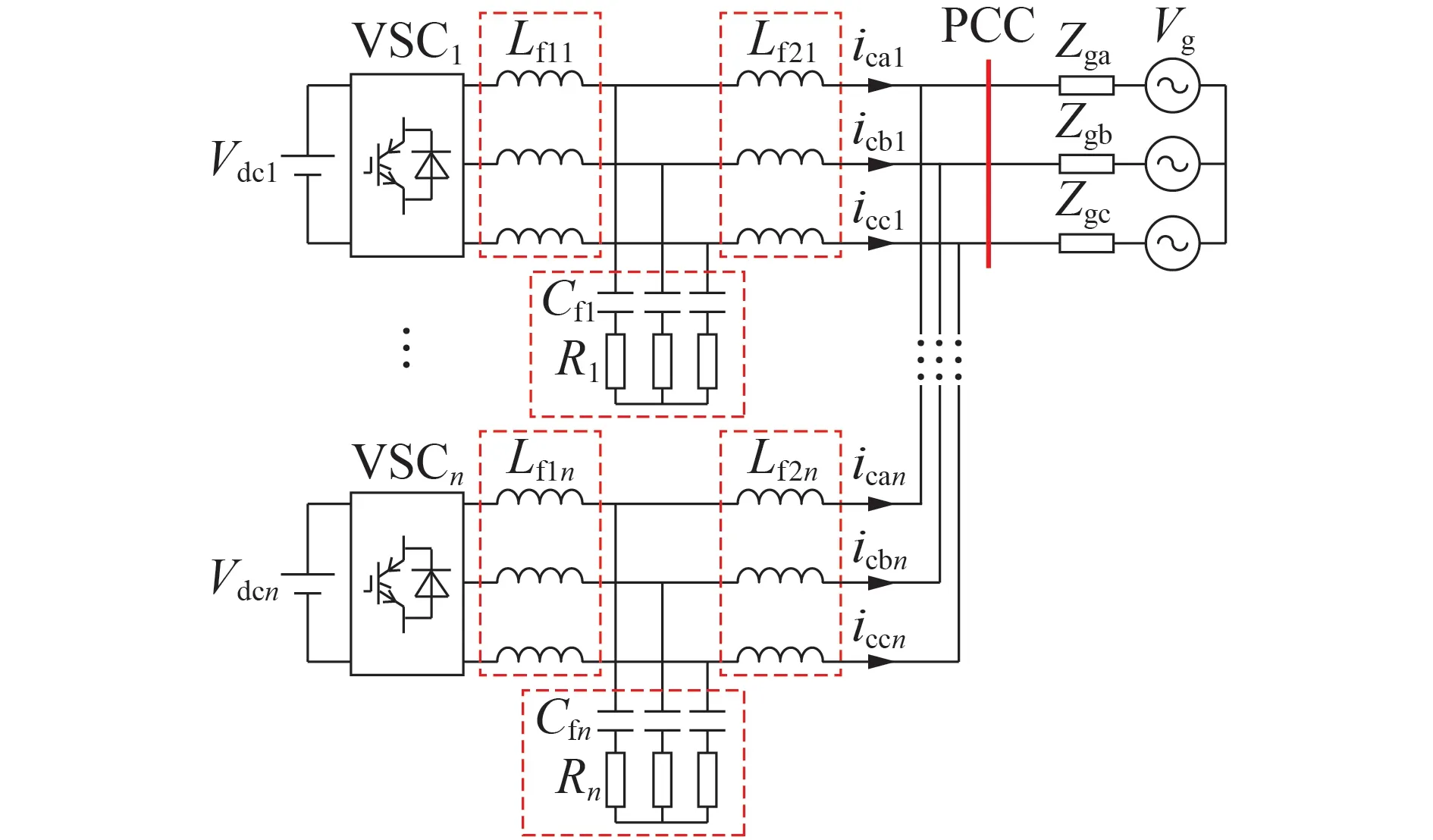
图1 多机并联示意图Fig.1 Schematic diagram of multi-VSC in parallel
为研究不对称电网下变流器多机并联系统的稳定性问题,采用附录A 图A1所示的双变流器并联简化模型,图中描述了不同变流器的控制策略。VSC采用PLL 实现电网同步,在α β控制框架下采用比例谐振(proportional resonant,PR)电流控制器实现电流控制。由于在不平衡电网中工作时传统的SRFPLL 不能实现准确的相位检测,本文选择NF-PLL 和DSOGI-PLL为研究对象[20,23-24]。
2 不平衡电网多机并联模型
下面首先推导PLL在复α β框架下的HTF模型,进一步推导出变流器在复空间α β框架下的小信号导纳模型,最后得到多机并联系统的复频域模型。
2.1 PLL建模
NF-PLL 的控制框图和小信号动态传播示意图见附录A 图A2。图中:Va、Vb、Vc为三相电网的相电压;ω1为电网基频角速度;e-jθ+=cosθ+-jsinθ+表示复空间中角度为θ+的Park变换;FNPLL(s)由100 Hz的陷波滤波器(notch filter,NF)的传递函数HNF(s)与PLL控制支路传递函数HPLL(s)级联组成,其对应的表达式分别见附录A式(A1)、(A2)。
三相不平衡电压经过Park 变换后,伴随直流分量存在的还有100 Hz 分量。由图A2 可知,NF-PLL的工作原理是在Park 变换后通过陷波滤波器模块滤除100 Hz 分量,导致引入了100 Hz 电压分量,即NF-PLL 中电压d轴分量Vcnotchd为LTP 变 量。Vcnotchd的Toeplitz矩阵Vcnotchd为:
式中:Vd为d轴直流分量的幅值;Vd-1和Vd+1分别为d轴-100 Hz 和100 Hz 分量的幅值。因此,NF-PLL 中存在3 种谐波分量相互作用,系统存在LTP 动态效应。定义“后滤波”类型的PLL为其100 Hz分量滤波模块是在Park 变换之后(如NF-PLL、DDSRF-PLL等)。所以,带“后滤波”类型PLL的VSC系统在不平衡电网工况下均表现出LTP特性。
DSOGI-PLL 的工作机理与NF-PLL 具有显著的不同,DSOGI-PLL 的控制框图见附录A 图A3(a)。由图可知,三相不平衡电压进入DSOGI-PLL 后,先经过DSOGI 模块进行“预滤波”,提取出了正序电压分量,从而消除dq轴电压中的100 Hz 分量,之后进行Park 变换得到的dq轴分量仅含直流分量。所以DSOGI-PLL中的d轴电压Vcsogid表现出LTI特性。
不平衡电网下DSOGI-PLL 的小信号动态传播示意图如附录A 图A3(b)所示。Vcsogid的Toeplitz 矩阵Vcsogid为:
DSOGI-PLL 的工作机理决定了DSOGI-PLL 在dq坐标系下的稳态运行工作点呈现LTI 特性。同样,定义“预滤波”类型的PLL 为其100 Hz 分量滤波模块是在Park 变换之前(如DSOGI-PLL、双降阶广义积分器锁相环(double reduced order generalized integrator-PLL,DROGI-PLL)等)。带“预滤波”类型PLL 的VSC 系统在不平衡电网工况下均表现出LTI特性。
同时相较于“后滤波”类型的PLL,“预滤波”类型的PLL 内不存在多个谐波的交互,显著削弱了多频率耦合效应。DSOGI 的传递函数矩阵Tsogi1(s)和Tsogi2(s)的推导见附录A式(A3)—(A8)。
结合图A3 可以推导出复空间下DSOGI-PLL 的输入电压到扰动相角ΔθDSOGI(s)之间的关系为:
式中:I0为单位矩阵;Δ(s)为正序q轴电压的扰动量矩阵;GSOGI(s)为+(s)到ΔθDSOGI(s)的传递函数。
NF-PLL 小信号模型的详细推导过程已在文献[20]中给出,本文不再赘述。
由式(3)可知,扰动相角Δθ在控制系统下受控制系统电压的d轴分量(如和)影响,Δθ进一步影响VSC 输出导纳的特性。包含±100 Hz 电压分量,即Vncotchd受控制系统中电压负序分量的影响。这也是PLL 中多频耦合现象的原因。由式(2)可以看出,由于DSOGI 模块的滤波作用,只包含直流电压分量。所以,在控制系统中,的值仅受电压正序分量的影响,即式(2)可以写为=Vd。
Vd-1和Vd+1的产生来源有如下2 个:不平衡电网阻抗导致的PCC 处不平衡电压Ugu;不平衡电网电压导致的PCC 处不平衡电压Uun。两者叠加在PCC 处的不对称电压记为Upu。对于VSC 的输出导纳建模不需要考虑电网阻抗,仅需考虑Upu对VSC 工作点的影响。在并网系统稳定分析时,需分别考虑Upu对VSC输出阻抗的影响以及电网阻抗自身的影响。
由上述分析可知,Upu改变了带NF-PLL 的VSC输出导纳矩阵的阶数,从而影响了系统的稳定性。带DSOGI-PLL的VSC的输出导纳不受Upu的影响,系统稳定性不受Upu的影响。这一结论可以进行推广。不平衡电网工况下,“预滤波”类型PLL 的谐波抑制能力较“后滤波”类型PLL 具有显著提升。带“后滤波”类型PLL 的VSC 输出导纳特性受Upu的影响较大,即系统稳定性也受影响。而带“预滤波”类型PLL 的VSC 输出导纳不受Upu的影响。并网交互系统中,若电网等效阻抗没发生改变,仅PCC处的负序电压大小发生改变,带“预滤波”类型PLL 的VSC 并网系统稳定性则不受影响。
故下文选取含“预滤波”和“后滤波”2 类PLL 的多VSC 并网系统进行不平衡电网工况下的稳定性分析。
采用DSOGI-PLL 的控制策略的参考电流复频域模型如式(4)所示,其小信号流程图如附录A 图A4所示。
式中:YPLL( )s表示PLL 对电流环的影响;I为Idqref的共轭。
此多输入多输出模型不仅表现了系统的相角依赖特性,还清晰地描述了频率之间的耦合关系。
2.2 变流器建模
图2 为复频域多频框架下的VSC 小信号模型。图中:Gd(s)为并网逆变器采用数字控制时的总延时传递函数矩阵,由计算延时、脉宽调制延时和采样开关三部分组成;Gr(s)为PR 控制器的传递函数矩阵;Y1(s)和Y2(s)为物理滤波器的传递函数矩阵[20];ΔIαβ为 电 流 扰 动 量;ΔIα*β为ΔIαβ的 共 轭。矩 阵Gd(s)、Gr(s)、Y1(s)和Y2(s)均是由传递函数通过频移组成的主对角矩阵。
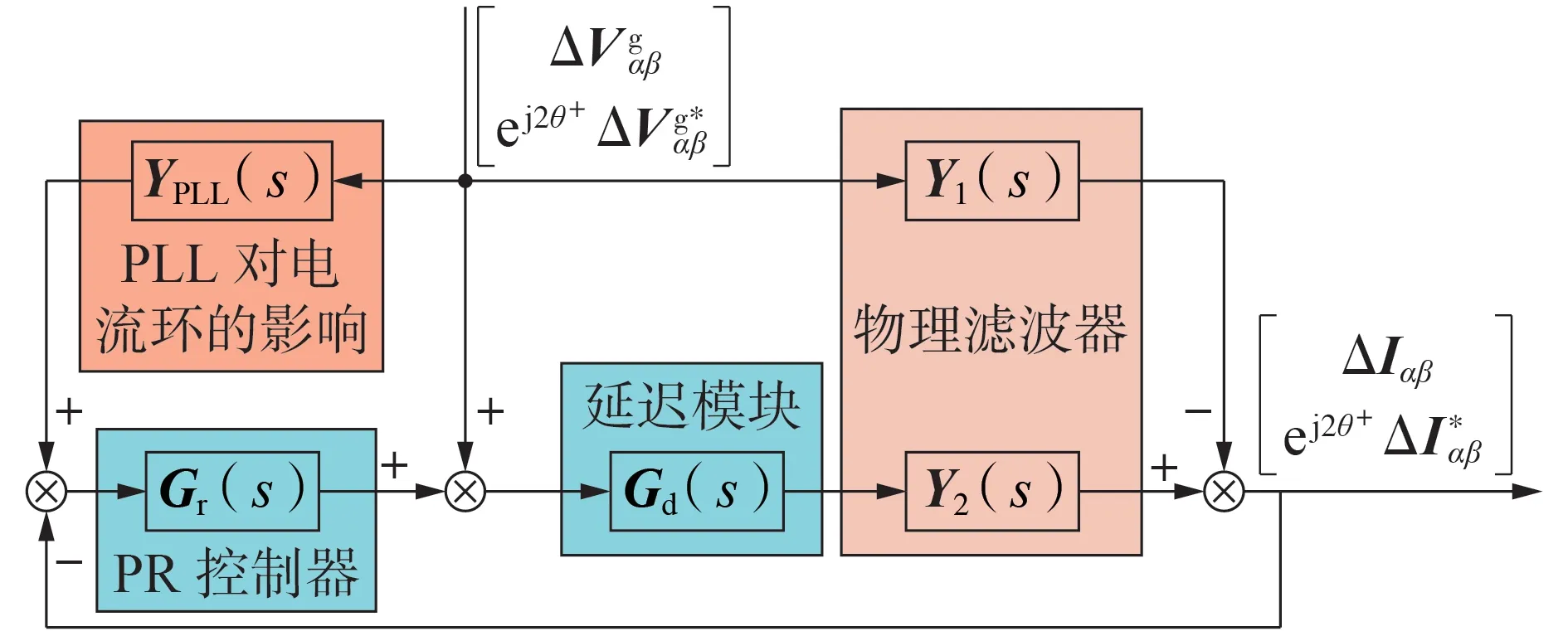
图2 复空间下VSC的信号框图Fig.2 Signal block diagram of VSC under complex space
根据图2 建立的系统闭环模型,推导出VSC 的导纳矩阵Y(s)表达式为:
式 中:YNF-PLL(s)和YDSOGI-PLL(s)分 别 为 带NF-PLL 和DSOGI-PLL 的VSC 的导纳矩阵。代入不同的YPLL(s)便可得到带不同PLL的VSC的导纳矩阵。
由式(7)可知,若VSC 带的是NF-PLL,向PCC 处注入频率为f的电压谐波,则VSC 的输出电流中将会出现频率为f、f-100 Hz、f+100 Hz、-(f-200 Hz)、-(f-100 Hz)和-f的谐波,其中频率为-(f- 200 Hz)的谐波分量较小。含这些频率的电流皆与频率为f的电压之间存在导纳关系。由式(8)可知,若VSC带的是DSOGI-PLL,则仅在频率为f和-(f-100 Hz)处存在谐波电流,电压、电流的耦合关系明显被削弱。值得强调的是,电网平衡与否对带DSOGI-PLL 的VSC 输出导纳表达式没有影响,即不会改变其频率耦合关系。本文考虑多VSC 并联模型的一致性,统一使用6×6阶矩阵表示。
2.3 扫频分析
双VSC 并联的导纳矩阵YM( )s是由4 个3×3 阶矩阵组成的,由于主对角线对稳定性的判定起主要作用,且矩阵内元素较多,这里仅展示4 个3×3 阶矩阵的主对角元素验证结果。频率耦合在基频附近最显著[20],本文展示0~100 Hz 对数坐标系下的扫频验证结果。VSC 的控制参数见附录A 表A1。同时注入25 % 的基频负序电压构造三相不平衡电网电压。线性化理论模型与仿真测量结果对比如附录A 图A5 所示。扫频结果验证了所建立模型的准确性,可以用于并网交互系统的稳定性分析。
3 不平衡电网多机并联系统稳定性分析
下面基于所建立的小信号导纳模型对电网不平衡条件下多机并联系统进行稳定性分析。
3.1 系统等效电路
基于阻抗的稳定性判据为评估电流源并网系统的稳定性提供了理论依据。并网变流器被等效为电流源与输出导纳的并联,如附录A图A6所示。
电网侧基于戴维南电路模型等效为理想电压源和电网等效阻抗的串联。利用对称分量法推导出电网不平衡下电网等效阻抗的表达式如下[19]:
式中:Zg11(s) =Zg22(s) =s(Zga+Zgb+Zgc);Zg12(s)=sZga+V*(s)]T和[I(s),I*(s)]T分别为αβ轴电压和电流映a2sZgb+asZgc,a=ej2π/3;Zg21(s) =sZga+asZgb+a2sZgc;[V(s),射到复频域的基向量。Zg为电网等效阻抗矩阵[20],ZgYM(s)为系统的小环路增益,故可以通过对M(s)=ZgYM(s)分析来确定多台变流器在电网三相阻抗不平衡时并网处的输出稳定性。
3.2 PLL的影响
为了研究带不同PLL 的双机并网交互系统在弱电网下的稳定性,需计及并联变流器的输出阻抗及电网参数进行整体分析。所研究并网系统的电气参数以及电流控制器的参数见附录A 表A1。2 个电流控制器设置相同的参数,通过参考电流表述不同机群的功率大小。
本文中电网三相等效阻抗值均仅计及电感值Lgy,当电网三相阻抗不平衡(Lga=6 mH、Lgb=3 mH、Lgc=2 mH)时,矩阵M( )s的奈奎斯特图见附录A 图A7,同时电网侧注入的负序电压幅值为正序电压的25 %。由图可知,系统的稳定性由特征根λ1反映。图3 为矩阵M( )s特征根λ1的伯德图。图中:配置1表示并网交互系统中2 台变流器均带NF-PLL;配置2 表示并网交互系统中变流器1 带NF-PLL、变流器2 带DSOGI-PLL。由图3 可以看出,失稳频率为99.97 Hz。这意味100 Hz 附近是系统稳定与否的关键频段。
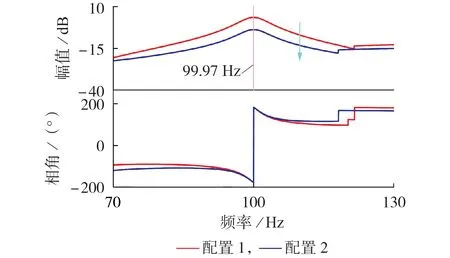
图3 带不同PLL系统的特征根λ1的伯德图Fig.3 Bode diagram of characteristic root λ1 of system with different types of PLL
为了寻找并网交互系统矩阵M(s)中主导特征根λ1幅相特性的元素,本文引入特征根的灵敏度这一概念。特征根灵敏度反映了矩阵中某元素的变化对特征根影响的大小,在系统稳定性分析中被广泛采用[25]。具体表达式为:
由式(10)可知,特征根λi对矩阵中元素akj的灵敏度等于左特征向量元素φik和右特征向量元素φji的乘积。矩阵中元素为复数,通过对计算结果取绝对值来表征元素对特征根大小的影响程度。
将频率f=99.97 Hz 代入M求解各元素对特征根λ1的灵敏度。M(s)k×j中各元素对特征根λ1的灵敏度见附录A 图A8。根据图A8 的计算结果选出灵敏度较大的元素(如图A8(a)中数值大于0.1 的元素),认为λ1在99.97 Hz处幅相特性的变化由这些元素主导。进一步提取主导元素进行分析。将矩阵M剩余元素近似为0,求取新矩阵M′的特征根。通过计算发现,存在2 个不为0 的特征根,而其中一个近似为0,另一个特征根与M(s)2×2几乎完全一致。这一现象说明在99.97 Hz 处M(s)2×2对矩阵M′ 的特征根起绝对主导作用。附录A 图A9 对比了矩阵M的特征根λ1的幅相特性(蓝色曲线)与M(s)2×2的幅相特性(绿色曲线)。综上,在99.97 Hz 处M(s)2×2对矩阵M的特征根λ1起主导作用。
以0.01 Hz 为步长,将f代入矩阵M中可得,在100 Hz附近M(s)2×2与T=Zg(2,2)×YM(2,2)的大小几乎完全一致,其幅相特性的对比如附录A 图A10所示。由图可知,M(s)2×2在100 Hz 附近可以用Zg(2,2)/(1/YM(2,2))近似表示。
通过上述计算与分析得出,并网交互系统在99.97 Hz 处的稳定性主要由变流器导纳YM(2,2)和电网阻抗Zg(2,2)决定。
不同PLL 配置的双机并联系统输出导纳在对数坐标系下的伯德图如附录A 图A11 所示。由图可知,当采用配置1 时,双机并联系统输出导纳的幅值在关键频率处大于配置2,而PLL的改变几乎没有影响关键频率处的相位。
综上,通过替换PLL类型,减小了并网变流器导纳YM(2,2)的幅值,进一步使系统的特征根λ1幅值从正值降至负值,改善了稳定性薄弱频率处的稳定裕度,增强了并网交互系统的稳定性。
3.3 并联多机的影响
通常通过并联新的变流器增加发电容量,但一般情况下系统中增加1 台变流器可能导致谐波不稳定。这一结论主要针对传统PLL 情况,本节针对并联新变流器后系统的稳定性提升进行分析。
下面同样基于电网三相阻抗不平衡的情况进行分析,即Lga=10 mH、Lgb=7 mH、Lgc=7 mH(电网4),同时电网侧注入的负序电压幅值为20 % 正序电压幅值。采用与3.2 节相同的方法寻找主导并网交互系统稳定性的元素。图4 为单VSC 和双VSC 的并网交互系统特征根λ1的伯德图。由图可知,单VSC 系统失稳频率为99.98 Hz。经计算发现,在失稳频率处,单VSC 和双VSC 的并网交互系统稳定性分别由单VSC 的输出导纳YNF-PLL(2,2)、双VSC 的输出导纳YM(2,2)和电网阻抗Zg(2,2)主导。
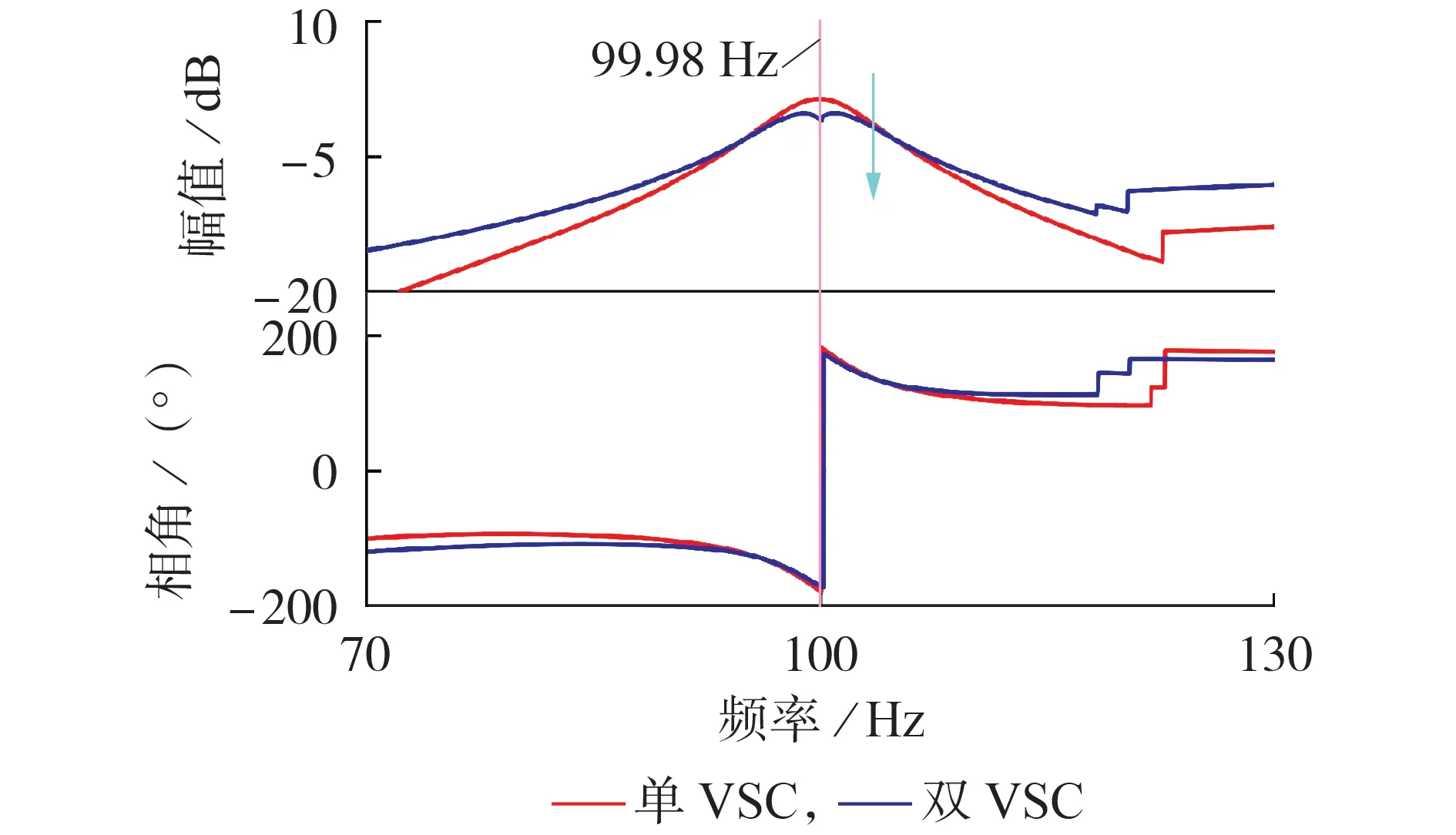
图4 系统特征根λ1的伯德图Fig.4 Bode diagram of characteristic root λ1 of system
对数坐标系下变流器输出导纳的伯德图见附录A 图A12。可以看出,单台带NF-PLL 的并网变流器在100 Hz附近导纳YNF-PLL(2,2)的幅值存在明显的上升现象,提高了系统的不稳定风险。并联1 台带DSOGI-PLL的变流器后,变流器的输出导纳YM(2,2)相比并联前的YNF-PLL(2,2)在100 Hz 附近存在20°左右的相角滞后。由图4 可知,当带DSOGI-PLL 的变流器并联至系统后,λ1的幅值和相角均发生了变化,在关键频率处的幅值减小为负值,系统处于稳定状态。
3.4 不平衡电压的影响
基于建立的VSC模型可知,不平衡电网工况下,Upu的改变将对含“后滤波”类型PLL 的多VSC 系统的导纳特性产生影响,进而产生稳定性问题。本节将详细分析Upu对并网交互系统稳定性的影响机理及趋势。下面选取带配置2的双机系统分析不同Upu下的稳定性问题。
电网等效阻抗选取三相不平衡工况:Lga=6 mH、Lgb=3 mH、Lgc=2 mH。通过调节注入基频负序电压来控制Upu大小。
图5 为注入不同基频负序电压大小时系统特征根λ1的伯德图。图中,25 % 表示注入的基频负序电压幅值为正序电压的25 %,其他以此类推。可以发现:系统特征根λ1在100 Hz 附近均出现了-180° 的相角穿越;随着电网不平衡度的增加,系统特征根λ1的幅值逐渐由负转正,系统状态由稳定转变为不稳定。
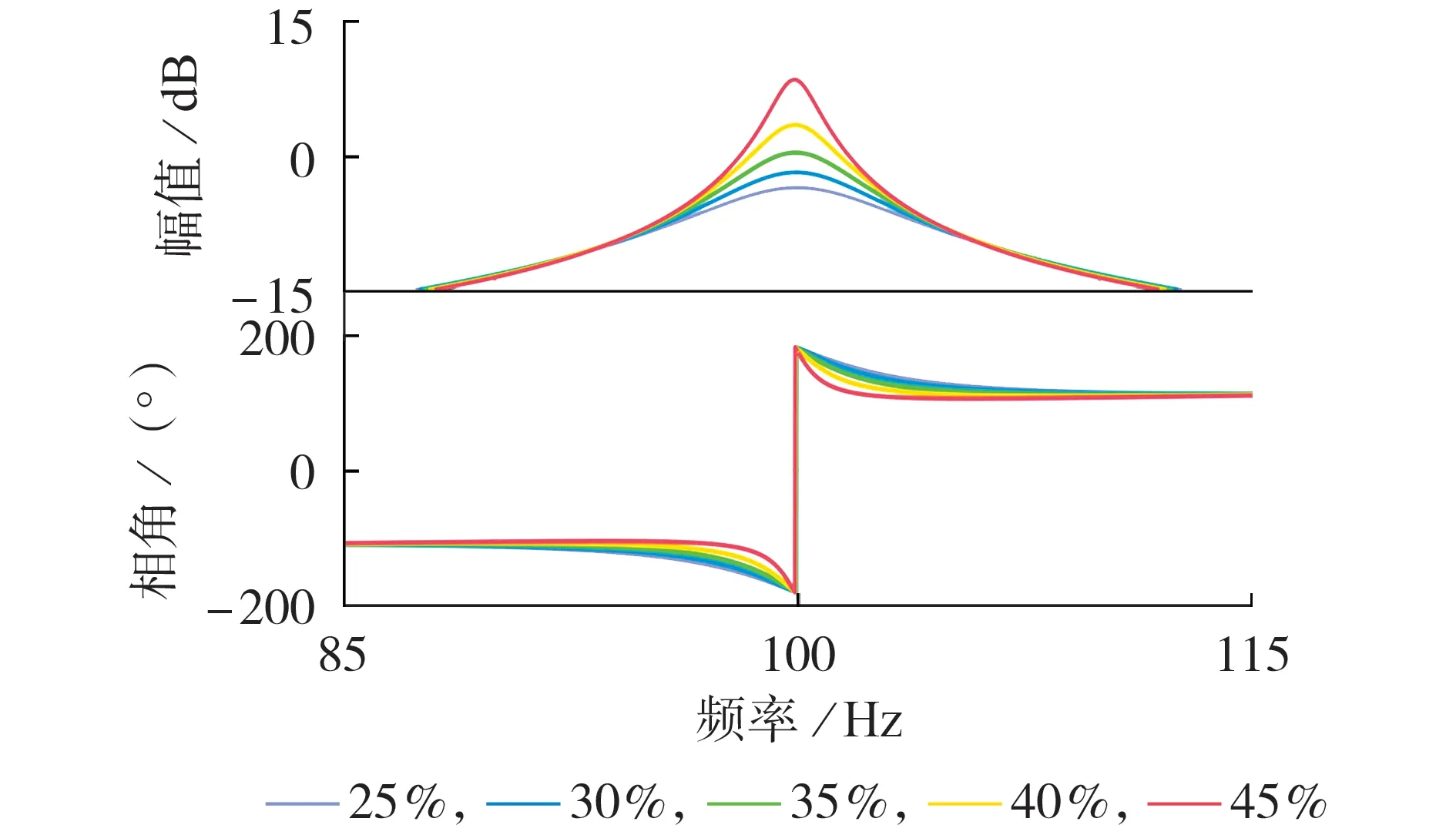
图5 并网交互系统特征根λ1的伯德图Fig.5 Bode diagram of characteristic root λ1 of grid-connected interactive system
基于上述分析,不同负序电压大小下变流器导纳YM(2,2)的频率响应见附录A 图A13。由图可知,负序电压大小的改变,仅改变100 Hz 附近的幅相特性。图中进一步展示了不同电网不平衡度下变流器输出导纳在100 Hz 附近的幅相特性。可以清晰地看出,随着电网不平衡度的增大,变流器输出导纳YM(2,2)的幅值随之增大,但它们在关键频率处的相角几乎是相等的。
由分析可知,PCC 处负序电压的增大,改变了带NF-PLL的VSC输出导纳,造成YM(2,2)幅值的增大,同时几乎没改变其关键频率处的相角,进而导致系统特征根λ1的幅值由负值向正值增长,最终致使并网交互系统的稳定裕度下降。
综上,增加PCC处的负序基频电压幅值,仅会使带“后滤波”类型PLL 的VSC 导纳特性改变,进而使得系统失稳。若2台均为带“预滤波”类型的PLL,且电网阻抗不变,则PCC 处基频负序电压幅值的增加将不影响系统的稳定状态。
4 仿真及实验验证
4.1 仿真验证
由于电网发生不对称故障后,电网等效阻抗表现出三相阻抗不对称的特点,故选取了4 组典型数据用于表征不对称电网下电网的强弱,如附录B 表B1 所示。表中:从电网1 到电网4,电网强度依次变弱,多VSC并网交互系统的稳定性也随之发生变化。
为了验证“后滤波”类型的PLL具有更好的频率耦合抑制作用,分别对带NF-PLL 和DSOGI-PLL 的VSC 进行仿真,并对VSC 的输出电流特性进行分析比较。在电网2 条件下,电网侧注入的基频负序电压幅值为正序电压的25 %。注入10 Hz 谐波分量,10 Hz谐波分量幅值为正序电压的10 %。
当不对称三相电网中存在低频小扰动时,带NF-PLL 和DSOGI-PLL 的VSC 输出电压和电流的时域波形分别如附录B 图B1(a)、(b)所示。由图可知:带NF-PLL 的VSC 输出电流存在多频耦合现象,总谐波畸变率(total harmonic distortion,THD)达到12.46 %;而带DSOGI-PLL 的VSC 输出电流更平滑,THD仅为2.63 %。
注入的基频负序电压幅值为正序电压的25 %时,PCC 处电压和电流的时域波形见附录B 图B2。由图B2(a)可知:配置1 在电网2 条件下,并网电流开始振荡发散,波形质量逐渐变差,同时PCC处电压也开始逐渐出现严重的不对称畸变,因此连接到电网的电流是不稳定的;而在电网1 条件下,并网电流波形轮廓平坦且质量一直很好,因此并网电流输出是稳定的。由图B2(b)可知:配置2 在电网2 条件下并网电流波形三相对称,并网交互系统处于稳定状态;当改变为电网3 条件时,并网电流波形质量开始逐渐变差,同时并网电压开始出现明显的不对称畸变,并网交互系统进入不稳定状态。对比图B2(a)、(b)可以看出,在弱电网条件下,配置2比配置1具有更好的稳定性,这与前文分析得出的结论一致。
图6 为单VSC 和双VSC 系统的PCC 处电压和电流时域波形对比,电网条件及控制参数与前文分析一致。由图可知,如果只连接带NF-PLL的并网变流器到电网,则并网处电压和电流均存在一定程度的振荡,此时系统是不稳定的。1 s 时,在并网处并联带DSOGI-PLL 的并网变流器。可以看出,当带DSOGI-PLL 的变流器与电网相互作用时,并网处电压和电流的时域波形就停止振荡,此时系统进入稳定状态。
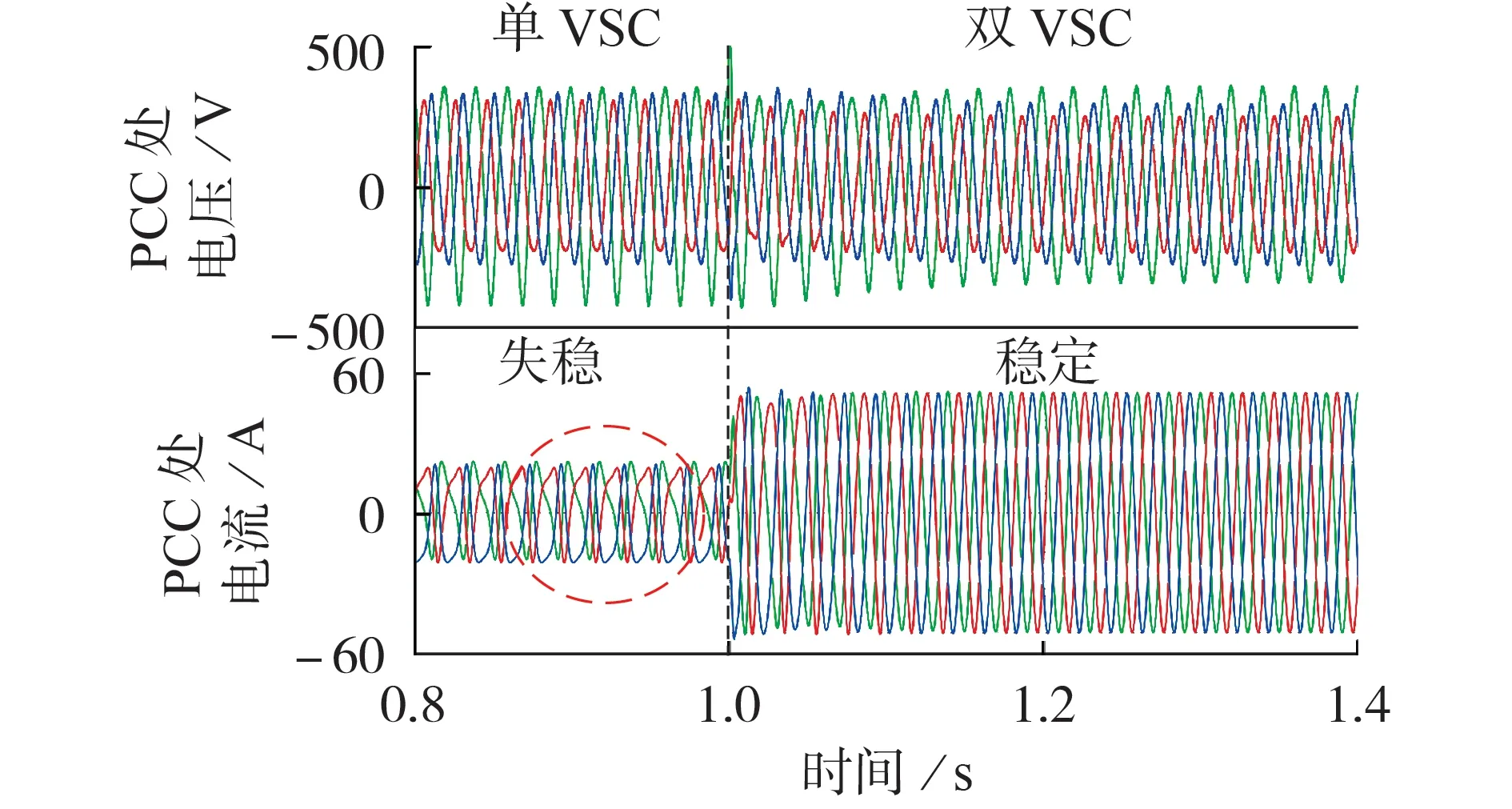
图6 单VSC和双VSC系统的电压、电流时域波形Fig.6 Time domain waveforms of voltage and current of single-VSC and dual-VSC systems
仿真结果表明,整个系统的稳定性得到了提高,与理论分析的结论一致。所以,DSOGI-PLL 在电网不平衡条件下,不仅表现出良好的控制性能,并且在系统稳定性方面也有着较好的表现。
双VSC系统在不同电网不平衡度下并网处的电压和电流时域波形见附录B 图B3。各案例的不平衡参数见附录B 表B2。Case 1 — 4 的并网逆变器参数见附录A 表A1。在1 s 时,基频负序电压分量从5 % 增大至25 %。可以看出,负序电压的增大带来了并网电压和电流的振荡,且波形也开始发生畸变,并网交互系统从稳定状态转入不稳定状态。由图B3(b)可知,将其中一台变流器的PLL 从NF-PLL 替换为DSOGI-PLL,系统在25 % 负序电压的条件下是稳定的。然而,继续增大负序电压至45 % 时,并网处电压、电流的畸变又开始出现,系统再次进入不稳定状态。这一结果与理论分析一致。
4.2 实验验证
为了进一步验证理论分析的正确性,利用基于PLEXIM的RT Box3开展硬件在环实验验证。
实验1 和实验2 均在电网2 条件下进行,实验3在电网4 条件下进行,实验4 和实验5 在电网2 的基础上分别注入5 % 和45 % 的负序电压。5 组实验中VSC均采用表A1所示的控制器参数及电流参考值。
双VSC系统采用配置1和配置2时并网电压、电流的实验结果分别见附录B 图B4(a)、(b)。可以看出,VSC 采用配置1 时,并网电压和电流中出现了明显的低频谐波。而采用配置2 时,电压、电流波形轮廓平坦,稳定性有了较好的改善。
图7 为单VSC 和双VSC 系统并网电压、电流的实验结果。可以看到,当带NF-PLL的VSC单独运行时,并网电流出现严重的不对称畸变,系统处于失稳状态。在0.2 s 并联1 台带DSOGI-PLL 的VSC 后,并网电流停止了振荡,系统进入稳定状态。
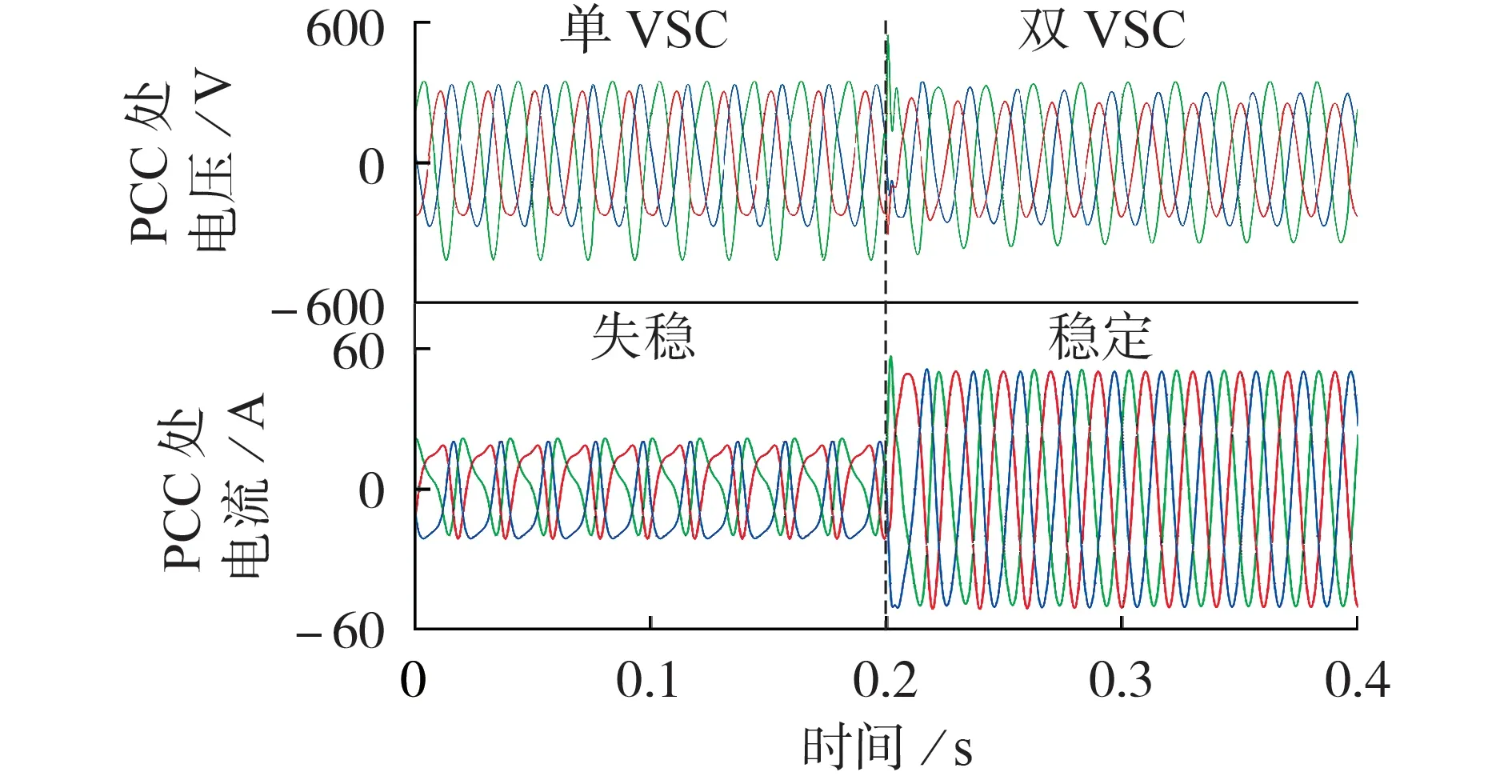
图7 实验3的电压、电流时域波形Fig.7 Time domain waveforms of voltage and current(Experiment 3)
不同电压不平衡度下并网电压、电流的实验结果分别见附录B 图B5(a)、(b)。实验4 中VSC 采用配置1,实验5 中VSC 采用配置2。结合实验1、2 的结果,可以得到电网不平衡度的增加对并网交互系统稳定性存在着负面影响的结论。
5 结论
本文针对三相不平衡电网,研究了不同工况下多VSC并联系统的稳定性问题。本文首先建立了三相不平衡电网下多VSC 并联导纳模型。基于此模型,研究了不平衡电网下多VSC 系统在不同工况下的稳定性及其关键环节之间的相互作用、耦合机理,并提出了提升稳定性的优化设计方法。理论分析、仿真以及实验表明:
1)相较于“后滤波”类型的PLL,“预滤波”类型的PLL能够更加有效地削弱系统的频率耦合;
2)用DSOGI-PLL 替换NF-PLL 可以提高三相不平衡电网下多VSC并联系统的稳定性裕度;
3)在带NF-PLL 的VSC 上并联一台带DSOGIPLL 的VSC 可以在提高系统输出功率的同时改善VSC并网交互系统的稳定性;
4)三相不平衡电网下,PCC 处基频负序电压幅值的增加,通过影响带“后滤波”类型的PLL 的VSC输出导纳,进而改变多VSC系统的导纳特性,最终导致系统失稳。
附录见本刊网络版(http://www.epae.cn)。
