系列决策任务中的策略转换：来自爱荷华赌博任务的证据*

胡馨允 沈 悦 戴俊毅

系列决策任务中的策略转换：来自爱荷华赌博任务的证据*

胡馨允 沈 悦 戴俊毅

(浙江大学心理与行为科学系, 杭州 310058)

已有大量研究使用系列决策任务探讨了各类决策的决策策略。通过假定个体采用单一策略完成所有任务试次, 并比较对应的计算认知模型拟合实证数据的能力, 这些研究发现各种决策任务都涉及多种可能的决策策略。但是, 此类研究的一个共同缺陷在于忽视了个体在任务过程中转换决策策略的可能性。通过开发允许在强化学习策略和启发式策略间转换的针对爱荷华赌博任务的计算认知模型, 并将此类模型同单一策略模型进行对比, 研究1提供了个体在该系列决策任务中会改变决策策略的明确证据。研究2则发现, 随着试次数的增加, 发生策略转换的可能性也会上升。这些结果表明, 为了正确认识各种决策任务的决策策略, 需要充分考虑在系列决策任务过程中发生策略转换的可能性, 尤其是试次较多的系列任务。未来研究可以探讨策略转换的多种可能形式, 以及导致策略转换的任务和个体因素, 以便进一步深化对于系列决策任务的心理机制的认识。

系列决策任务, 爱荷华赌博任务, 策略转换, 计算认知建模, 强化学习和启发式策略

1 引言

古人云“明者因时而变, 知者随事而制”, 当重复面对任务结构相同的决策(即完成系列决策任务)时, 人们所使用的决策策略不是一成不变的。1本文探讨的系列决策任务有别于序列决策任务, 后者一般是指后续决策的方案集合取决于之前的决策及其结果, 即时间上相邻的决策存在明显的动态依存性的决策任务。大量研究表明, 各种决策任务都存在多种不同的决策策略。例如, 针对多属性决策任务, 存在一系列不同的补偿式(选项在不同属性上的优势和劣势可以相互抵消)和非补偿式策略(选项在不同属性上的优势和劣势不可相互抵消, 例如, Payne et al., 1988; Rieskamp & Otto, 2006; Walsh & Gluck, 2016), 而面对风险决策任务时, 个体则可能采取基于期望效用或类似评估的策略(例如, Kahneman & Tversky, 1979; Von Neumann & Morgenstern, 1944)或者更为简单的启发式策略(例如, Brandstätter et al., 2006)。此外, 研究者还对信息环境、任务要求以及个体差异等因素如何影响个体的策略选择进行了探索(例如, Bergert & Nosofsky, 2007; Pachur & Galesic, 2013), 并且发现, 任务环境或者要求的变化可能会带来相应的决策策略的转换(例如, Bröder & Schiffer, 2006; Lee et al., 2014)。

除了由任务环境和要求的变化所导致的策略转换以外, 人们是否还可能在相对稳定的任务环境和要求下, 由于自我调整、适应或者内在的探索动机而发生策略转换？在绝大多数有关决策策略的实证研究中, 被试都需要在相同的任务结构下完成一系列决策试次, 以便研究者能够依托足够多的信息, 来推断被试的决策策略。虽然过往研究已经探讨了面对特定决策任务时个体所使用的策略的多样性, 以及影响策略选择的可能因素, 却鲜有研究考察, 在面对一个相对稳定的系列决策任务时, 个体的决策策略发生转换的可能性。如果这种可能性的确存在, 那么以往有关决策策略的研究, 就会因为忽视这一可能性而导致错误的结论。为了更好地探明个体在面对各种决策任务时的决策策略, 首先需要回答的问题是, 在任务环境和要求相对稳定的系列决策中, 是否的确会发生策略转换。本文将以爱荷华赌博任务这一典型的系列决策任务为例, 探讨这一重要的理论和实践问题。

爱荷华赌博任务(Iowa Gambling Task, IGT)是一项基于经验的模拟决策任务, 它最初是为了考察腹内侧前额叶损伤患者在应对不确定的现实情境时的决策缺陷而提出的(Bechara et al., 1994)。该任务包含4个牌堆(分别标记为A, B, C, D), 被试需要多次在这些牌堆间做出选择。每次选择某一牌堆之后, 都会抽取并翻转其最上方的一张牌, 并根据牌面信息给予被试一定的奖励。但是, 有时选择某一牌堆也会同时给被试带来损失。在任务开始之前, 被试并不知道每个牌堆的盈亏规律以及总试次数, 而他们的目标则是通过他们的选择获得尽可能高的总回报。因此, 被试需要通过不断选择各个牌堆来学习每个牌堆的盈亏规律, 并采取特定策略来完成这一任务。目前IGT已被广泛用于识别各种临床人群的决策缺陷, 包括脑损伤人群(Hochman et al., 2010)、药物滥用人群(Ahn et al., 2014; Bechara & Damasio, 2002; Bechara et al., 2001)、神经疾病人群(Stout et al., 2001)以及精神障碍人群(李蕾等, 2019; 徐四华, 2012)等。

除了被用于考察临床人群的决策缺陷, IGT还被用来探究正常和临床人群在面对不确定情境时的决策策略。为此, 研究者们提出了对应不同策略的一系列计算认知模型, 这些模型大致可分为强化学习模型和启发式模型两类。强化学习模型假设IGT包含三个过程：涉及动机的对每次选择结果的评估过程, 涉及认知的对牌堆期望效价的更新过程, 以及涉及反应的概率化选择过程。Busemeyer和Stout (2002)提出了第一个针对IGT的强化学习模型——期望效价学习(Expectancy-Valence Learning, EVL)模型。该模型假定个体使用期望效用(Expectancy Utility, EU)函数来评估每次选择结果的效用(Ahn et al., 2008), 使用差异学习(Delta-Learning, DEL)规则来更新每个牌堆的期望效价(Rescorla & Wagner, 1972), 并使用依赖于试次的选择(Trial-Dependent Choice, TDC)规则来指导下一试次的选择(Luce, 1959)。在EVL模型的基础上, Ahn等人(2008)进一步探索了强化学习模型涉及的三个过程中每个过程的不同数学形式, 并提出了预期效价学习(Prospect- Valence Learning, PVL)模型。该模型假定个体会使用预期效用(Prospect Utility, PU)函数(Kahneman & Tversky, 1979)对选择的净收益(即奖励以及可能同时出现的损失之和)进行评估, 使用Erev和Roth (1998)提出的衰减强化学习(Decay-Reinforcement Learning, DRL)规则更新预期效价, 并且使用不随试次变化的选择(Trial-Independent Choice, TIC)规则(Yechiam & Ert, 2007)做出反应。更为近期的采用系统化模型比较方法的研究表明(Dai et al., 2015), 个体在对结果进行评估时, 更有可能会对同时出现的奖励和损失首先分别按照预期效用函数进行评估, 然后再将评估结果加以整合。对应的模型被称为第2类预期效价学习(Prospect-Valence Learning 2, PVL2)模型。

在有关IGT的启发式模型中, 最有代表性且拟合实证数据表现最好的是赢留输走(Win-Stay-Lose- Shift, WSLS)模型(Worthy et al., 2012)。该模型假设, 人们的每次选择仅取决于上一次选择的牌堆以及所得的结果, 而与更早之前的选择及其结果无关。因此, 相比于考虑之前所有试次的选择及对应结果的强化学习模型, WSLS模型假设的心理机制更为简单。具体而言, 该模型假定个体继续选择相同牌堆的概率, 受当前选择该牌堆的结果而定。如果当前选择的净收益非负(即赢), 则有较大可能继续选择相同牌堆, 反之(即输), 则有较大可能下一试次转而选择不同的牌堆。

尽管关于IGT的决策策略已经有了丰富的研究成果, 但很少有研究考虑个体在完成IGT过程中发生策略转换这一可能。Busemeyer和Stout (2002)曾提出过一个策略转换启发式选择(Strategy-Switching Heuristic Choice)模型。但是, 该模型所谓的“策略转换”, 并非是指决策策略的本质变化, 而是指随着个体由于选择不利牌堆(即A或B牌堆)遭受越来越多的损失, 其选择概率在不利牌堆和有利牌堆(即C或D牌堆)之间重新分配的过程。此外, 也有研究者提出了将强化学习和启发式策略结合在一起的计算认知模型。例如, Worthy等人(2013)提出了效价附加坚持(Valence-Plus-Perseverance, VPP)模型。该模型认为, 在IGT的每一个试次中, 人们都会综合考虑各个牌堆的期望效价以及前一试次的选择及其结果, 再决定当前试次的选择。虽然该模型同时包含强化学习和启发式策略成分, 且相比于EVL、PVL以及WSLS模型, 该模型在拟合实证数据时有较好的表现, 但它仍然假定个体会使用单一的, 虽然更为复杂的混合策略来完成IGT中每个试次的选择。

综上所述, 有关IGT的决策策略研究, 尚未考察在任务过程中发生策略转换这一可能。如果个体的确会在任务过程中因为各种原因转变决策策略, 那么以往仅仅比较单一策略模型的研究, 就可能得出关于个体策略选择的错误认识。此外, 那些根据单一策略模型的参数估计, 来推断不同人群决策差异背后的心理机制的研究(例如, Ahn et al., 2014; Yechiam et al., 2005), 也可能会产生有偏的估计, 进而导致对人群差异的错误解读。本研究将通过开发允许策略转换的模型并将其与传统的单一策略模型进行比较, 来回答在IGT中是否存在策略转换这一问题, 以期为得出有关IGT中的决策策略以及不同人群差异的更为可信的结论提供依据, 也为在更大范围内探讨决策策略转换这一重要的理论和实践问题提供借鉴。

2 研究1：IGT策略转换模型的提出和检验

2.1 方法

2.1.1 IGT简介

如上所述, IGT包含4个牌堆(分别标记为A、B、C、D), 在每个试次中被试需要选择一个牌堆, 并根据其最上方的牌呈现的信息获得一定的奖励, 并有可能同时遭受一些损失。被试的目标是在总试次数未知的情况下, 使总回报最大化。例如, 在Bechara等人(1994)最早的IGT研究中包含了(被试未知的)100个试次, 并且采用了如表1所示的支付方案。具体而言, 被试每次选择A或B牌堆, 都会获得100美元的收益。但是, 每选择10次A牌堆, 被试都会遭受5次损失, 金额从小到大分别为150美元、200美元、250美元、300美元和350美元, 且这5次损失在每10次选择中出现的具体位置都会有所变化。类似的, 被试每选择10次B牌堆, 都会遭受1次金额为1250美元的损失, 且每10次选择中出现损失的位置也各不相同。对于C或者D牌堆, 每次选择都会带来50美元的收益。然而, 每选择10次C牌堆, 都会遭受5次总额为250美元的损失, 每选择10次D牌堆, 则会遭受1次250美元的损失, 且每10次选择C或D牌堆遭受损失试次的位置也会有所不同。后续研究使用了相同或者类似的任务设置, 主要的调整发生在试次数, 以及是否使用真实回报两方面。当使用真实回报(即按照被试最后的总回报支付酬金)时, 出于控制实验经费的目的, 一般会将Bechara等人最初的支付方案中的各种结果金额都缩减100倍(例如, Dai et al., 2015)。无论采取何种支付方案, 所有类型的IGT研究都满足以下三点：1) A和B牌堆每次选择都有较高的收益, 但总损失也较大, 因此长期而言是不利的, 即总回报为负; 2) C和D牌堆每次选择的收益较低, 但总损失较小, 因此长期而言是有利的, 即总回报为正; 3) A和C牌堆相比于B和D牌堆会出现更多次的损失。

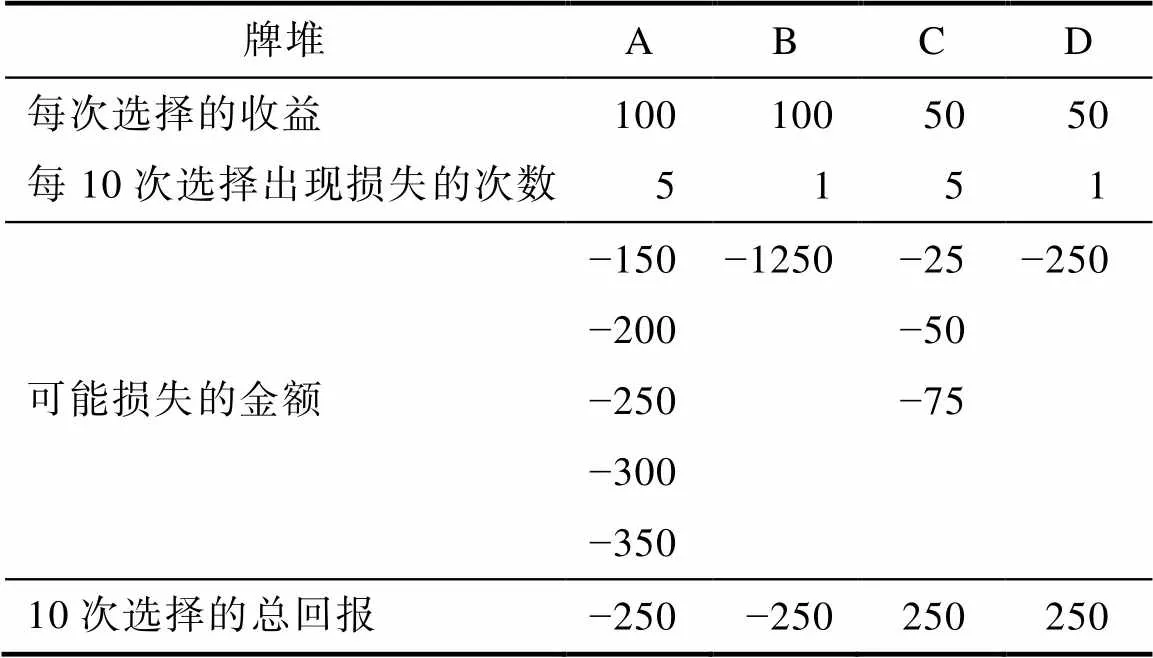
表1 Bechara等人(1994)使用的IGT支付方案

2.1.2 单一策略模型

为了给探究IGT中的策略转换提供合适的对照模型, 本研究考虑了已有文献中的三大类单一策略模型, 即强化学习模型, 启发式模型以及混合模型, 并以PVL2模型, WSLS模型和VPP模型作为各类模型的代表。这些模型在以往的研究中都有较好的表现, 因此如果新的允许策略转换的模型能够比它们有更好的表现, 则能为IGT中存在策略转换提供支持。以下将介绍这三个计算认知模型的具体数学形式。

针对IGT的强化学习模型假定人们通过结果评估、期望(或预期)效价更新和概率化选择三个过程来完成该任务。根据PVL2模型(Dai et al., 2015), 人们在选择某一牌堆之后, 会针对当前选择获得的收益和可能的损失, 使用预期理论的价值函数分别进行评估, 然后再做汇总。其对应的效用函数被称为第2类预期效用(Prospect Utility 2, PU2)函数, 效用评估的具体形式如下：

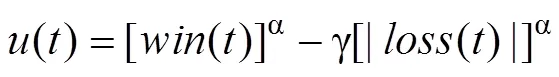
其中,()和()分别代表在试次获得的收益及可能同时出现的损失金额,()代表试次的汇总效用评估。α是形状参数, 用于衡量被试感受到的效用对于客观价值的敏感性, 取值范围在0到1之间, γ则代表预期理论中的损失厌恶参数, 取值范围在0到5之间。

在完成了结果评估之后, 根据PVL2模型, 个体会使用衰减强化学习规则对各牌堆的预期效价进行更新, 具体形式如下：

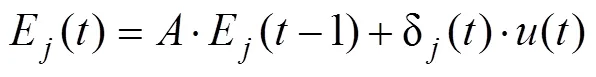
最后, PVL2模型假定, 个体会依据各牌堆的预期效价, 使用以下函数确定下一次选择各牌堆的概率并相应地做出随机选择(Sutton & Barto, 1998)：

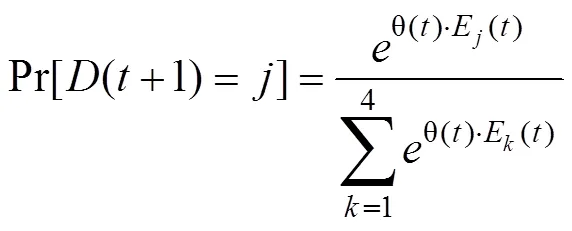
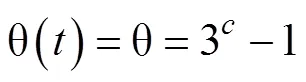
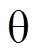
作为启发式模型的代表, WSLS模型假定的决策策略比PVL2模型假定的策略明显更为简单。根据该模型, 个体只会根据上一次选择的牌堆及其净收益(即收益和损失的总和), 来概率性地决定下一次的选择。该模型有两个参数, 第一个参数代表上一次选择的牌堆得到的净收益大于等于0时, 个体继续选择该牌堆的概率, 即

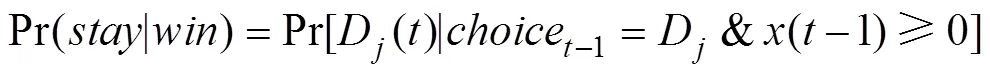
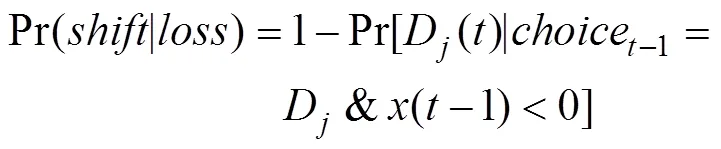
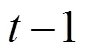
除了强化学习模型和启发式模型, Worthy等人(2013)提出的混合策略VPP模型也有很好的表现。Worthy等人认为, 使用衰减强化规则的强化学习模型混淆了坚持选择同一牌堆的倾向和选择预期效价最高的牌堆的倾向。因此, 他们分离了这两种倾向, 并提出了VPP模型。根据该模型, 个体一方面会使用PU函数来对某次选择结果进行效用评估, 并使用差异学习规则更新牌堆的预期效价, 其具体形式如下：

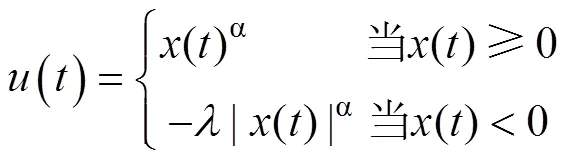
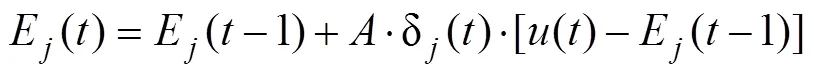
其中,()表示当前试次选择结果的净收益, 其他符号的含义同上文。

另一方面, 个体还会根据之前试次是否选择了牌堆以及选择牌堆所得净收益是否非负来确定当前试次坚持选择牌堆的倾向, 具体形式如下：

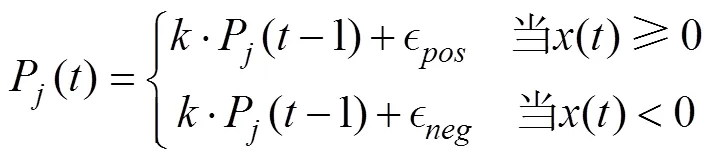
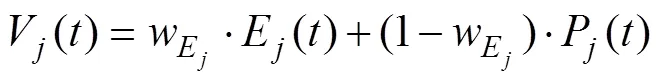
最后, 和PVL2模型类似, VPP模型假设被试会根据牌堆的价值确定下一次选择各牌堆的概率并相应地做出随机选择, 具体规则如下：

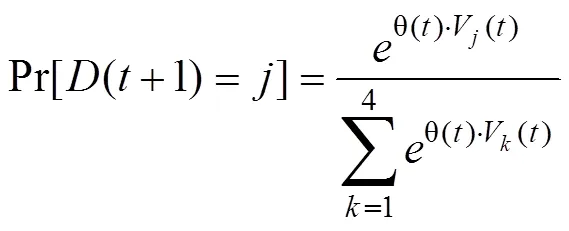
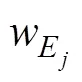
2.1.3 策略转换模型

由于IGT一般包含多达100个甚至更多的试次, 在整个任务过程中, 个体可能由于各种原因发生策略转换。在本研究中, 我们假定可能存在两种转换, 一种是在任务开始阶段由于缺乏信息而使用对信息依赖度较低的启发式策略, 并在对各牌堆有了更多了解之后, 转而使用更为复杂更为精细的强化学习策略。另一种则是在初始阶段就使用强化学习策略, 并随着任务的进行, 因为疲劳、倦怠或者降低认知负荷的需求, 转而采用启发式策略。从建模角度, 鉴于PVL2模型在强化学习模型, 以及WSLS模型在启发式模型中的优势地位, 本研究将分别以这两个模型来表达可能的强化学习策略和启发式策略, 并由此探讨个体在IGT中发生策略转换的可能性。

具体而言, 我们开发了一个允许发生一次策略转换(Switching-Strategy-Once, SSO)的模型。该模型假设个体在完成IGT的过程中, 会在启发式策略和强化学习策略之间进行一次转换, 且个体在使用启发式或者强化学习策略完成IGT时所使用的具体计算认知机制, 和对应的WSLS或者PVL2模型所假定的机制相同。除了WSLS模型和PVL2模型涉及的参数以外, 该模型还包含两个新的参数, 分别代表发生策略转换的节点试次, 记作(即Switching Point), 以及策略转换的类型, 记作(即Switching Type)。= 1代表个体在完成IGT的过程中先使用了强化学习策略, 之后转而使用启发式策略, 而= 2则代表相反的策略转换过程。因此, 该模型共有8个参数, 即涉及强化学习策略的α, γ,和, 涉及启发式策略的Pr(|)和Pr(|), 转换节点参数, 以及转换类型参数。由于当策略转换节点位于整个任务的开始或结尾阶段时, 相应的策略转换模型和对应的单一策略模型可能过于类似, 难以分辨。因此, 在本研究中, 我们将的范围限定在第21个试次到倒数第21个试次之间。

2.1.4 数据

为了系统比较策略转换模型和单一策略模型拟合实证数据的能力, 我们选取了以往采用IGT的研究中具有代表性的一系列数据集作为模型拟合对象(Steingroever et al., 2015)。具体而言, 这些数据出自10项研究, 涵盖了不同年龄范围的共617名健康被试, 且IGT的试次数包含95, 100和150三种情况。所有研究中的IGT都在计算机上完成, 且支付方案与表1所示的Bechara等人(1994)所用的方案相同或类似。所涉及的各项研究的基本信息参见Steingroever等人的表1。

2.1.5 模型拟合和比较方法

本研究所考察的每个计算认知模型(即WSLS, PVL2, VPP和SSO), 都可以根据被试之前的选择以及所得结果, 预测下一试次每个牌堆被选择的概率(即一步向前预测, Ahn et al., 2008)。因此, 我们首先使用极大似然估计法(Maximum-Likelihood Estimation, MLE), 用每个模型去拟合个体被试的选择数据, 即找到每个模型下, 可以使得实际选择数据出现可能性最大化的参数取值组合, 并以相应的观测数据的预测出现概率, 作为模型拟合表现的初步指标。具体而言, 在特定模型参数取值下的似然值被定义为该取值下, 模型预测的个体被试的选择序列的发生概率, 而对数似然值(Log-Likelihood, LL)则被定义为

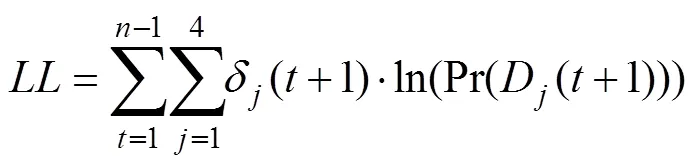
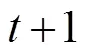
一般而言, 更为复杂的模型会有更好的拟合表现。由于上述模型的参数个数不尽相同, 它们的复杂程度也不尽相同。因此, 我们使用包含二阶偏差修正的赤池信息准则(Akaike Information Criterion with second-order bias correction, AICC; Akaike, 1974; Sugiura, 1978)和贝叶斯信息准则(Bayesian Information Criterion, BIC; Schwarz, 1978)这两种常用的适用于极大似然估计的指标, 来综合考量模型的拟合情况和复杂程度, 并以相应的准则分数来评价每个模型的表现并进行模型选择, 具体计算方式如下：

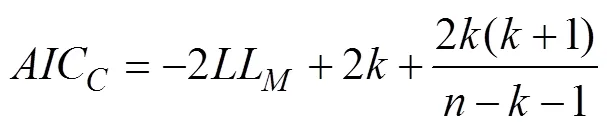
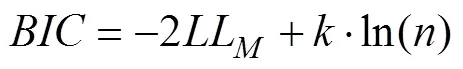
其中,代表模型的自由参数个数,为需要拟合的数据点个数(即总试次数− 1), 而LL则是指模型的极大对数似然值。AICC(或BIC)的值越小, 表示模型表现越好(Broomell et al., 2011)。2当样本量与模型参数个数的比值较小(即样本量/参数个数< 40)时, 使用包含二阶偏差修正的赤池信息准则(AICC)能够弥补使用AIC可能导致的过拟合缺陷(Burnham & Anderson, 2004)。因此, 在本文中我们使用AICC而非AIC作为模型评估的一个指标。

2.1.6 模型复原测试

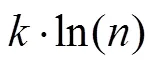
在本研究中, 我们对数据集中的617名被试的观测数据进行了模型拟合, 从而得到了每个被试在每个模型下的最优拟合参数取值。然后, 对于每个模型, 我们用对应于每名被试的最优拟合参数取值产生3组模拟数据, 共产生1821 (= 617 × 3)组模拟的被试数据。之后, 我们分别使用WSLS模型、PVL2模型、VPP模型和SSO模型, 用拟合观测数据一样的方法拟合这些模拟数据。最后, 通过分析使用不同指标(即AICC和BIC)时模型的区分度, 我们可以选取出更为合理的针对观测数据的模型选择指标。

2.2 结果

2.2.1 模型拟合和比较

表2展示了各个模型拟合全部617名被试的观测数据的结果。当以AICC为模型选择指标时, 无论是就群体均值还是个体结果而言, SSO模型都表现最佳, 而VPP、PVL2和WSLS模型的表现则依次变差。当以BIC为模型选择指标时, 就群体均值而言, PVL2模型的表现最佳, SSO模型次之。从个体结果上看, WSLS模型和PVL2模型表现较好, 分别在30.79%和33.87%的被试数据上有最好的表现, 而VPP和SSO模型的表现则基本相当。无论采用AICC还是BIC作为指标, SSO模型都在一部分被试的数据(AICC：43.27%, BIC：18.96%)上有最好的表现。

2.2.2 模型复原测试

由于AICC和BIC对于模型复杂度的惩罚程度存在差异, 相比于BIC, AICC倾向于选择参数更多的模型。因此, 出现使用AICC指标时, 较为复杂的VPP和SSO模型有更好的表现并不奇怪。为了选择更合适的模型选择指标, 我们进行了模型复原测试。表3和表4展示了模型复原测试的结果。当以AICC为模型选择指标时, 各模型有较好的区分度。对于每个模型产生的模拟被试数据, 该模型本身都能在最大比例的个体模拟数据上有最好的表现。而当以BIC为模型选择指标时, 对于每个模型产生的模拟数据, 最为简单的WSLS模型都能在最大比例的个体模拟数据上有最好的表现, 即BIC不能很好地对WSLS和其他模型进行区分。因此, 在本研究中, 相比于BIC, 将AICC作为模型选择指标更为合适。

注：表中的每一行代表不同模型在某个模型产生的模拟被试数据上的表现情况。例如, 第一行代表各个模型拟合WSLS模型产生的模拟被试数据时的表现。在由WSLS模型产生的模拟被试数据中, WSLS模型在88.60%的个体数据上表现最佳, 而PVL2模型、VPP模型和SSO模型则分别在3.67%、0.92%和6.81%的个体数据上表现最佳。

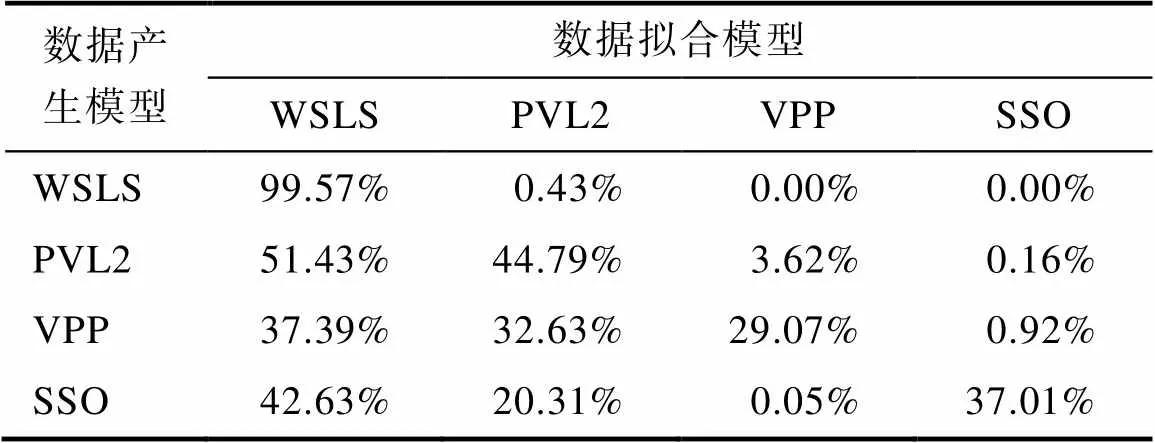
表4 研究1基于BIC的模型复原测试结果

注：表中内容的含义同表3。

2.3 讨论

本研究提出了有关IGT的一次策略转换模型, 并针对以往617名健康被试的数据, 比较了此模型和假定单一策略的具有代表性的PVL2模型(强化学习策略), WSLS模型(启发式策略)以及VPP模型(混合策略)的数据拟合表现。当分别以AICC和BIC作为模型选择指标时, 模型表现的相对优劣有所差异, 但策略转换模型都能在一定比例的个体数据上有最好的表现。模型复原测试的结果表明, AICC比BIC更适合在当前研究中被用于进行模型选择, 因为相比于使用BIC, 在使用AICC时更可能还原出正确的数据产生模型。当以AICC作为模型选择指标时, SSO模型无论从群体还是个体水平都要优于另外三个模型, 而且策略转换模型在近一半(43.27%)的被试观测数据上表现最佳。这些结果表明, 个体在完成IGT的过程中, 的确有较大可能会发生决策策略的转换。

如前所述, 经验累积或者疲倦等因素可能是造成在像IGT这样的系列决策任务中发生策略转换的原因。当任务的试次数变得越来越多时, 我们可以合理地认为, 经验累积或者疲倦这样的因素更有可能发生作用, 因而个体也就更有可能在任务过程中, 变换决策策略。因此, 作为本研究主体部分的补充, 我们还比较了包含不同试次数的IGT研究中的模型表现, 以便进一步考察策略转换的可能性。在本研究考察的617名被试中, 有15人完成的是95试次的IGT, 504人完成的是100试次的IGT, 还有98人完成的是150试次的IGT。表5展示了包含不同试次数的IGT数据以AICC为模型选择指标的相应结果。可以看出, 随着试次数的上升, 无论是从AICC均值, 还是从模型表现最好的被试比例来看, 策略转换模型相比于其他模型的优势都在增强, 这一点在模型表现最好的个体被试比例上表现得尤为明显, 即从13.33%上升到了53.06%。

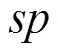
表5 研究1中根据试次数分组的模型拟合和比较结果

需要指出的是, 虽然上述分析支持IGT中可能存在策略转换, 但这些分析所考察的数据出自不同的研究, 在任务设置的细节上不尽相同, 而且试次数的范围和间距不尽合理, 完成不同试次数IGT的人数也很不均衡。因此, 以上分析结果只能被认为是为支持IGT中的策略转换提供了有限的证据。在以下报告的研究2中, 我们在对试次数进行更为合理的操纵的前提下, 采用相同的任务设置在每种试次数下收集了人数几乎相同的被试数据, 以便更好地检验试次数增加会提升策略转换的可能性这一关键假设。

3 研究2：试次数对IGT中策略转换可能性的影响

3.1 方法

3.1.1 被试

本研究采用实验范式操纵IGT的试次数, 并设置了100试次和200试次两个实验条件。共招募321名成年大学生被试(男性134人, 女性187人), 平均年龄20.54岁(= 2.41)。其中160人完成了100试次的IGT, 另161人则完成了200试次的IGT。招募被试时要求非心理学专业且未参加过IGT研究。所有被试均在实验前填写知情同意书, 并自愿参与实验。实验结束后, 被试会得到基础报酬和额外奖励, 额外奖励的数量和IGT的绩效有关, 绩效越高, 额外奖励越多。

3.1.2 实验设计与流程

本实验采用单因素被试间设计, 考察并比较不同试次数下个体在IGT中发生策略转换的可能性。本实验共设置100试次和200试次两种实验条件, 前者是大多数IGT研究的标准设置, 而后者则可以在控制实验总时长的前提下, 有效地拉开与前者的距离, 以实现一定程度的效应量。

任务开始前, 被试会阅读有关IGT的标准化介绍, 并被告知拥有2000元研究货币(即初始总财富)。任务开始后, 被试会看到分别位于屏幕上、下、左、右侧的4个牌堆, 并可以通过键盘的“上”、“下”、“左”、“右”键, 选择对应的牌堆。被试在完成任务之前, 并不知晓所需完成的试次数。每次选择完成后, 屏幕中央将呈现当前试次的奖励和损失, 以及更新之后的总财富额(如图1)。设置以上下左右方式呈现牌堆, 是为了减少传统的从左到右的排布方式对牌堆选择产生的非随机的影响, 例如在开始阶段依次选择A、B、C、D四个牌堆, 以及在后续试次中, 相继选择空间上明显相邻的牌堆。此外, 本研究采用和表1所示相同的支付方案, 且每10次选择某一牌堆时损失出现的试次位置也是随机的。实验程序使用Python3及PsychoPy软件编写, 被试需要在电脑的PsychoPy软件上完成实验。

图1 研究2实验界面截图

3.1.3 数据分析

本研究采用和研究1相同的模型拟合和比较技术, 分析和比较了3个单一策略模型和一次策略转换模型在拟合个体IGT数据时的表现, 并且进行了模型复原测试。此外, 使用独立样本比例差异检验, 分析试次数对于IGT中发生策略转换的可能性的影响。

表6 研究2模型比较结果

表7 研究2基于AICC的模型复原测试结果

注：每个单元格中的前一个数值代表100试次组的结果, 后一个数值代表200试次组的结果。

3.2 结果

3.2.1 模型拟合和比较

因模型复原测试表明, 在本研究中使用AICC仍然比使用BIC更有可能做出正确的模型选择(见下文), 此处仅报告基于AICC的结果。表6呈现了以AICC为标准, 100和200试次组各自的模型比较结果。无论是从群体均值, 还是从个体结果来看, SSO模型在两种试次数条件下都表现最佳。而且, 无论是针对100试次IGT还是200试次IGT, SSO模型都在至少一半被试的个体数据上有最好的表现。此外, 和研究1一样, VPP、PVL2和WSLS模型的表现依次变差。独立样本比例差异Z检验的结果表明, 200试次下发生策略转换的可能性(即SSO模型在拟合个体观测数据时表现最佳的比例, 65.22%), 高于100试次下发生策略转换的可能性(50.00%,= 2.76, 单侧= 0.003, 比例差异的95% CI = [0.045, 0.259], Cohen’s= 0.31, 对应较小的效应量)。

和在研究1中一样, 我们还分析了两种试次数条件下, SSO模型拟合最优的那些被试的参数的估计结果。当IGT包含100试次时,估计值的均值为47.03, 标准差为20.39; 当IGT包含200试次时,估计值的均值为95.38, 标准差为54.21。4在本研究以及研究1中, SSO模型拟合最优的被试的sp平均估计值都接近于允许范围的中间值。造成这一结果的可能原因是, 发生策略转换的个体的策略转换节点位于模型允许范围内的各个位置的可能性大致相当, 且整体分布呈单峰形态。单侧Mann-Whitney检验结果表明, 无论在哪种转换类型下, 200试次下的平均转换节点均显著晚于100试次下的平均转换节点(值均小于0.001)。

3.2.2 模型复原测试

本研究使用每个模型模拟了3×321 = 963组个体被试数据, 并使用4个模型对每组模拟数据进行了拟合。表7展示了100试次组和200试次组基于AICC的模型复原测试结果。不论是在100试次还是200试次下, 所考察的每个模型都能在最大比例的各自模型产生的模拟数据上有最好的表现。总体而言, 试次数为200时数据生成模型被正确复原的比例(71.74%), 要高于试次数为100时的比例(64.69%,= 4.70, 单侧< 0.001, 比例差异的95% CI = [0.041, 0.100], Cohen’s= 0.15, 对应小的效应量)。

表8展示了基于BIC的模型复原测试结果。可以看出, 和研究1一样, 当使用BIC进行模型选择时, 几乎在所有情况下, 无论针对哪个模型产生的个体模拟数据, WSLS模型都能有最好的表现, 即BIC不能很好地对WSLS和其他模型进行区分。只有当试次数为200时, PVL2模型和SSO模型才能在各自产生的模拟数据上有最好的表现。总体而言, 试次数为200时数据生成模型被正确复原的比例(59.06%), 要高于试次数为100时的比例(49.17%,= 6.16, 单侧< 0.001, 比例差异的95% CI = [0.068, 0.130], Cohen’s= 0.20, 对应小的效应量)。

3.3 讨论

本研究的目的在于考察试次数的增加是否会导致被试在IGT中更有可能发生策略转换。结果表明, 无论IGT包含标准的100个试次还是更多的200个试次, 和研究1类似, 策略转换模型都在至少一半被试的个体数据上有最好的表现。更为重要的是, 同包含100个试次的IGT相比, 当IGT包含200个试次时, 策略转换模型在更高比例的个体数据上表现最佳。这意味着, 当试次数为200时, 人们更有可能在IGT中发生策略转换。这一结果排除了策略转换模型能够在部分被试的数据上有最好的表现, 仅仅是由模型比较结果的随机性所致这一解释, 从而为个体在像IGT这样的系列决策任务中可能发生策略转换提供了进一步的支持。此外, 模型复原测试的结果表明, 与BIC相比, AICC仍然是更有可能做出正确的模型选择的指标。因此, 本研究继续使用AICC作为模型选择和策略推断的依据。最后, 无论是采用AICC还是BIC作为模型选择指标, 200试次下的模型复原表现, 都要优于100试次下的表现。这与更大的数据量将有助于更好地区分不同模型的传统看法是一致的。

表8 研究2基于BIC的模型复原测试结果

注：表中内容的含义同表7。

4 总讨论

系列决策任务既广泛存在于我们的日常生活中, 也大量出现在有关决策策略和影响因素的实证研究之中。例如, 为了招聘各种岗位的职员, 人力资源部门的员工需要频繁地在求职者间做出选择, 而像IGT这样的需要被试在相同的任务结构下重复完成多次决策的实验室任务也比比皆是。以往有关系列决策任务下的决策策略的研究, 一般假设个体在所有试次中都使用相同的策略。之所以要求进行多次重复决策, 仅仅是为了给推断决策策略提供更多的信息。但是, 在这样的决策任务中, 人们不仅会了解和学习任务刺激的具体特征, 而且可能在更高的水平上, 学习和相应地调整他们的决策策略。对于后一种学习的充分了解, 将有助于我们得出有关策略选择的更为准确的推断, 并且考察影响策略选择及其转换的因素, 从而更好地为改善决策服务。

本研究以IGT为对象, 较为系统地探讨了人们在系列决策任务中发生策略转换的可能性。结果表明, 人们不仅会在IGT中发生策略转换, 而且这一转换的可能性, 还会随着任务试次数的上升而有所提升。这表明, 在通过各种系列决策任务探讨个体的决策策略时, 需要充分考虑策略转换的可能性, 尤其是在任务试次数较多的情况下。具体而言, 可以参照本文所报告的方式, 开发允许策略转换的计算认知模型, 并将它们和假定单一策略的模型进行比较, 从而推断个体是否发生了策略转换, 以及在何时发生了策略转换。由此, 研究者有望对个体在任务不同阶段的策略使用情况有更加准确的认识, 后续基于不同阶段的模型参数估计的分析, 也更有可能产生相对准确的推断。

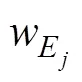
在确认了系列决策任务存在策略转换的可能性后, 一个需要进一步探讨的关键问题是, 产生策略转换的条件是什么, 或者说怎样的任务因素、个体因素或者两者的交互可能引发策略转换。例如, 当任务难度或者自身的抱负水平较高时, 个体可能因为现有策略无法实现目标, 而选择尝试不同的策略。由此可以推断, 通过增大任务难度(比如要求在IGT中必须使得财富水平有所增长)或者提升个体的抱负水平的方式, 也许能够引发更多的策略转换。此外, 是否存在优势策略也是影响策略转换的一个可能因素。当个体在尝试了不同策略并且发现了优势策略之后, 其策略转换的倾向可能会有所减弱。反之, 如果多种策略下的任务表现大致相当, 那么发生策略转换的可能性则将取决于个体希望尽可能有更好的表现的意愿, 以及探索不同策略的动机程度。对于策略转换诱发因素的考察, 将进一步提升我们对于决策策略及其转换的认识。

Ahn, W. Y., Busemeyer, J. R., Wagenmakers, E. J., & Stout, J. C. (2008). Comparison of decision learning models using the generalization criterion method.(8), 1376−1402. https://doi.org/10.1080/03640210802352992

Ahn, W. Y., Vasilev, G., Lee, S. H., Busemeyer, J. R., Kruschke, J. K., Bechara, A., & Vassileva, J. (2014). Decision-making in stimulant and opiate addicts in protracted abstinence: Evidence from computational modeling with pure users.849. https://doi.org/10.3389/ fpsyg.2014.00849

Akaike, H. (1974). A new look at the statistical model identification.(6), 716−723.

Bechara, A., Damasio, A. R., Damasio, H., & Anderson, S. W. (1994). Insensitivity to future consequences following damage to human prefrontal cortex.(1−3), 7−15. https://doi.org/10.1016/0010-0277(94)90018-3

Bechara, A., & Damasio, H. (2002). Decision-making and addiction (part I): Impaired activation of somatic states in substance dependent individuals when pondering decisions with negative future consequences.(10),1675−1689. https://doi.org/10.1016/s0028-3932(02)00015-5

Bechara, A., Dolan, S., Denburg, N., Hindes, A., Anderson, S. W., & Nathan, P. E. (2001). Decision-making deficits, linked to a dysfunctional ventromedial prefrontal cortex, revealed in alcohol and stimulant abusers.(4), 376−389. https://doi.org/10.1016/s0028-3932(00)00136-6

Bergert, F. B., & Nosofsky, R. M. (2007). A response-time approach to comparing generalized rational and take-the- best models of decision making.107−129.

Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs.409−432.

Bröder, A., & Schiffer, S. (2006). Adaptive flexibility and maladaptive routines in selecting fast and frugal decision strategies.904−918. https://doi.org/10.1037/ 0278-7393.32.4.904

Broomell, S. B., Budescu, D. V., & Por, H. H. (2011). Pair-wise comparisons of multiple models.(8), 821−831.

Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: Understanding AIC and BIC in model selection.(2), 261−304. https://doi.org/10.1177/0049124104268644

Busemeyer, J. R., & Stout, J. C. (2002). A contribution of cognitive decision models to clinical assessment: Decomposing performance on the Bechara gambling task.(3), 253. https://doi.org/10.1037/1040-3590. 14.3.253

Clerc, M. (2010).(Vol. 93). John Wiley & Sons.

Dai, J., Kerestes, R., Upton, D. J., Busemeyer, J. R., & Stout, J. C. (2015). An improved cognitive model of the Iowa and Soochow Gambling Tasks with regard to model fitting performance and tests of parameter consistency.299. https://doi.org/10.3389/fpsyg.2015.00229

Erev, I., & Roth, A. E. (1998). Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria.(4), 848−881. https://jstor.org/stable/117009

Fang, J., Schooler, L., & Shenghua, L. (2023). Machine learning strategy identification: A paradigm to uncover decision strategies with high fidelity.(1), 263−284.

Hochman, G., Yechiam, E., & Bechara, A. (2010). Recency gets larger as lesions move from anterior to posterior locations within the ventromedial prefrontal cortex.(1), 27−34. https:// doi.org/10.1016/j.bbr.2010.04.023

Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk.(2), 263−292. https://jstor.org/stable/1914185

Lee, M. D., & Gluck, K. A. (2021). Modeling strategy switches in multi-attribute decision making.148−163. https://doi.org/10.1007/ s42113-020-00092-w

Lee, M. D., Gluck, K. A., & Walsh, M. M. (2019). Understanding the complexity of simple decisions: Modeling multiple behaviors and switching strategies.(4), 335−368. https://doi.org/10.1037/dec0000105

Lee, M. D., Newell, B. R., & Vandekerckhove, J. (2014). Modeling the adaptation of search termination in human decision making.(4), 223−251. https://doi.org/ 10.1037/dec0000019

Li, L., Zhang, J. Q., Hou, J. W., Li, Y. L., Lu, Y. J., & Guo, Z. J. (2019). Decision-making characteristics assessed by the IOWA Gambling Task in schizophrenia: A meta-analysis.(6),688−691, 695.

[李蕾, 张俊青, 侯继文, 李亚铃, 鲁玉洁, 郭宗君. (2019). 爱荷华赌博任务评估精神分裂症决策特点Meta分析.(6), 688−691, 695.]

Luce, R. D. (1959).New York: Wiley.

Pachur, T., & Galesic, M. (2013). Strategy selection in risky choice: The impact of numeracy, affect, and cross-cultural differences.260−271.

Payne, J. W., Bettman, J. R., & Johnson. E. J. (1988). Adaptive strategy selection in decision making.534−552.

Rescorla, R. A., & Wagner, A. R. (1972). A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In A. H. Black, & W. F. Prokasy (Eds.),(pp. 64−99). Appleton-Century-Crofts.

Rieskamp, J., & Otto, P. E. (2006). SSL: A theory of how people learn to select strategies.(2), 207−236. https://doi.org/ 10.1037/0096-3445.135.2.207

Schwarz, G. (1978). Estimating the dimension of a model.,(2), 461−464.

Steingroever, H., Fridberg, D. J., Horstmann, A., Kjome, K. L., Kumari, V., Lane, S. D., … Wagenmakers, E. J. (2015). Data from 617 healthy participants performing the Iowa Gambling Task: A “Many Labs” Collaboration.(1), e5. http://doi.org/10.5334/ jopd.ak

Stout, J. C., Rodawalt, W. C., & Siemers, E. R. (2001). Risky decision making in Huntington's disease.(1), 92−101. https://doi.org/10.1017/s1355617701711095

Sugiura, N. (1978). Further analysis of the data by Akaike’s information criterion and the finite corrections.13−26. http://doi.org/10.1080/03610927808827599

Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction.(5), 1054−1054. https://doi.org/10.1109/tnn.1998.712192

Von Neumann, J., & Morgenstern, O. (1944).Princeton University Press.

Wagenmakers, E. J., Ratcliff, R., Gomez, P., & Iverson, G. J. (2004). Assessing model mimicry using the parametric bootstrap.28−50. https://doi.org/10.1016/j.jmp.2003.11.004

Walsh, M. M., & Gluck, K. A. (2016). Verbalization of decision strategies in multiple-cue probabilistic inference.(1), 78−91. https://doi.org/10.1002/bdm.1878

Worthy, D. A., Hawthorne, M. J., & Otto, A. R. (2012). Heterogeneity of strategy use in the Iowa gambling task: A comparison of win-stay/lose-shift and reinforcement learning models.(2), 364−371. https://doi.org/10.3758/s13423-012-0324-9

Worthy, D. A., Pang, B., & Byrne, K. A. (2013). Decomposing the roles of perseveration and expected value representation in models of the Iowa gambling task.640. https://doi.org/10.3389/fpsyg.2013.00640

Xu, S. H. (2012). Internet addicts’ behavior impulsivity: Evidence from the Iowa Gambling Task.(11), 1523−1534.

[徐四华. (2012). 网络成瘾者的行为冲动性——来自爱荷华赌博任务的证据.(11), 1523−1534.]

Yechiam, E., Busemeyer, J. R., Stout, J. C., & Bechara, A. (2005). Using cognitive models to map relations between neuropsychological disorders and human decision-making deficits.973−978.

Yechiam, E., & Ert, E. (2007). Evaluating the reliance on past choices in adaptive learning models.(2), 75−84. https://doi.org/10.1016/j.jmp. 2006.11.002

Strategy switching in a sequence of decisions: Evidence from the Iowa Gambling Task

HU Xinyun, SHEN Yue, DAI Junyi

(Department of Psychology and Behavioral Sciences, Zhejiang University, Hangzhou 310058, China)

Much research has been devoted to studying decision strategies in various tasks. Such research usually involved a sequence of decision trials under the same task structure to provide sufficient information for inferring the underlying decision strategies. By assuming each individual adopted a single decision strategy across all decision trials and comparing corresponding computational cognitive models in terms of their performances in fitting empirical data, such studies have revealed multiple possible decision strategies for many major decision tasks. One common drawback of such research, however, was overlooking the possibility that individuals switched their strategies along the sequence of decisions. This might lead to inappropriate conclusions regarding the decision strategies underlying specific decision tasks or misleading inferences of potential cognitive and affective differences between normal and different clinical populations based on parameter estimates from models assuming single strategies.

To address this critical issue, two studies were conducted to examine the possibility of strategy switching in the Iowa Gambling Task (IGT), an experience-based decision task with a sequence of trials aimed at mimicking real-world decisions under uncertainty. By developing a computational cognitive model that allowed for switches between reinforcement learning strategies and heuristic strategies and comparing its performance with those of single-strategy models, Study 1 showed that data from about half of the 617 healthy participants in 10 previous studies were better fitted by the strategy-switching model than three single-strategy models that performed well in previous research, that is, the WSLS, PVL2, and VPP models as exemplar models assuming heuristic, reinforcement learning, and mixed strategies, respectively. This result provided clear support for the possibility of strategy switching in the IGT.

Since strategy switching might occur with accumulating experience or fatigue and an increasing number of trials is likely to facilitate such changes, 321 participants were recruited in Study 2 to further examine whether a larger number of trials would contribute to more strategy switching in the IGT. Specifically, 160 participants performed a 100-trial IGT, whereas the other 161 participants performed a 200-trial IGT under otherwise the same task structure. It was found that data from a larger proportion of individual participants were best fitted by the strategy-switching model when the IGT involved 200 trials rather than standard 100 trials. This result provided further evidence for strategy switching in the task.

Overall, the current results suggest that strategy switching is likely to occur in a sequence of decisions under the same task structure. Consequently, in order to obtain proper understanding of the decision strategies for various decision tasks, it is necessary to consider seriously the possibility of strategy switching, especially for a long sequence of decisions. For a more refined understanding of psychological mechanisms underlying sequences of decisions, future research might further investigate various forms of strategy switching such as gradual instead of abrupt switches and task and individual factors that trigger such switches.

decision task with a sequence of trials, The Iowa Gambling Task, strategy switching, computational cognitive modeling, reinforcement learning and heuristic strategies

2023-02-02

* 中央高校基本科研业务费专项资金(2018QNA3014)资助。

戴俊毅, E-mail: junyidai@zju.edu.cn

B842.1