基于生成对抗网络的scRNA-seq批次效应校正方法
2023-11-10陈立鑫
陈立鑫,林 劼
(1.福建师范大学数学与统计学院,福建 福州 350117;2.福建师范大学计算机与网络空间安全学院,福建 福州 350117)
单细胞转录组测序(scRNA-seq)是从单个细胞的层次上对基因组、转录组、表观组进行高通量测序分析以及分析异质性免疫细胞亚群和细胞间变异对生物过程影响的一项强有力的技术,能够在单个细胞水平上研究细胞的基因表达,可以更有针对性地研究和分析生物数据,因此scRNA-seq数据挖掘研究逐步成为生物信息学的重要研究方向[1].单细胞转录组测序数据通常是从多个实验中汇编而来的,捕获时间、处理人员、试剂批次、设备甚至技术平台都不同,这些差异导致数据产生巨大差异或批次效应,并可能在数据集成期间混淆感兴趣的生物差异[2].因此,降低批次效应是必不可少的.通过对批次效应进行校正,可以将不同批次的样本“标准化”,消除批次效应对于数据的影响,从而提高数据的准确性和可靠性,并且更好地揭示生物学差异,帮助科学家更好地理解生物学现象.
单细胞测序数据的批次效应校正问题面临着3大挑战:一是单细胞测序数据通常包含大量的细胞及基因,因此需要考虑如何处理高维数据,以避免过拟合和维度灾难等问题;二是单细胞测序数据可能由多个批次组成,每个批次的细胞数也不同,因此需要对不同批次下样本数量和质量进行平衡,以确保校正的有效性;三是由于技术限制和生物因素,单细胞转录组测序中存在“dropout”事件,即某些基因表达值非常低或接近于零,出现“假零”[3].
本文针对单细胞测序数据的批次效应问题,提出了一种基于生成对抗网络的批次效应校正算法scBCMGAN,通过构建一个编码器作为生成器(generator),构建一个判别器(discriminator),组成一个生成对抗网络(generative adversarial networks,GAN).假设scRNA-seq数据服从ZINB分布,通过该分布捕获scRNA-seq 数据分布的高稀疏性和过度分散性[4],使用其似然损失作为重构损失,将编码器的潜在层输出作为判别器的输入,通过损失优化使得判别器无法区分源(source)批次样本和目标(target)批次样本,然后应用解码器进行数据重构,以训练整个模型使其达到纳什均衡状态,最后修改目标批次样本的批次信息为目标批次实现批次效应校正.本方法校正结果不会改变数据维度,能够用于下游分析.本文共分为4个部分:第一部分对已有的批次效应校正算法进行介绍;第二部分将介绍本文所提出的方法,包括模型架构和算法;第三部分对实验进行详细阐述,包括数据预处理、实验结果展示以及结果分析;第四部分进行总结与展望.
1 相关工作
目前针对单细胞测序数据的批次效应校正方法主要可以分为3大类:基于对齐的方法、基于神经网络的方法和基于统计分析的方法.
基于对齐的方法如由Haghverdi等[5]开创的mutual nearest neighbors(MNN)方法,该算法首先识别跨批次的相互最近邻(MNN)以在两个数据集之间建立连接,所得到的成对细胞列表用于计算平移向量以将数据集对齐到共享空间.由于需要计算高维基因表达空间中的邻居列表,因此该方法会受计算时间和内存方面的影响.考虑到MNN中计算最近邻需要计算不同批次细胞之间的成对距离,在基因数目较多的情况下,计算量较大,因此,fastMNN[6]先通过PCA对原始基因表达矩阵降维,而后在降维后的空间中计算最近邻和校正批次效应,虽然计算速度提升,但也失去了在基因水平上的可解释性.Scanorama[7]通过SVD计算每个细胞的基因表达值的压缩低维嵌入,然后利用局部敏感哈希算法和随机投影树来计算批次内细胞在其他批次的k个最近邻以获得相互最近邻.但Scanorama在混合批次的同时,也混合了细胞类型[8],并且该方法较适用于10x Genomics数据[9].Harmony[10]使用迭代聚类方法来对齐来自不同批次的细胞,将不同批次的数据集组合并使用PCA将数据投影到维度较小的空间中,然后使用迭代过程来消除多数据集特定的影响.Seurat multiCCA(Seurat 2)[11]通过使用典型相关分析(CCA)将2个数据集降维,映射到一个低维空间中,采用动态时间扭曲算法将2个数据集对齐到一个共同的基准尺度,产生对齐的低维嵌入.Seurat Integration (Seurat 3)[12]使用CCA进行降维,在子空间中识别跨批次的MNN,使用共享最近邻图评估细胞类型相似性,选出置信度较高的“锚点”,最终在原始数据集中完成校正.scMerge[13]首先使用高度可变基因(HVG)在数据中通过搜索相互最近的集群以构建一个连接批次之间细胞簇的图,将稳定表达的基因(SEG)用作负例对照估计不需要的因素,然后使用移除不需要的变化(RUV)模型来捕获数据集之间不需要的变化并进行删除,实现校正.
基于神经网络的方法如MMD-ResNet[14],该方法基于2个数据集的分布之间的差异适中的假设,训练一个残差网络来学习从一个分布到另一个分布的映射,最小化在不同批次中测量的2个多元分布之间的最大平均差异来进行校正批次效应.scGen[15]结合变分自编码器构建模型来学习参考数据集中细胞的分布,通过训练好的网络预测查询数据集的分布,结合特定的网络结构来进行批次效应校正.
基于统计的方法如ComBat[16],使用贝叶斯方法将数据拟合到标准分布,以估计存在的批次效应,然后使用计算出的批次效应估计器来校正原始基因表达矩阵.limma[17]将输入数据拟合到具有阻塞项的线性模型以捕获批次效应,然后从原始数据中减去捕获的批次效应,以获得批次效应校正后的表达矩阵.ZINB-WaVE[18]是RUV模型的扩展,使用零膨胀负二项分布 (ZINB)回归对具有技术和生物学效应的数据进行建模,ZINB-WaVE 将ZINB模型拟合到数据,从而产生类似于PCA的因子模型,然后从原始数据中去除存在的批次效应,以产生校正后的基因表达矩阵.LIGE[19]采用迭代学习方法来表征批次数据以进行校正,首先使用综合非负矩阵分解 (iNMF)学习一个低维空间,使用共享因子空间并构建共享因子邻域图来连接具有相似因子加载模式的细胞以识别数据集中的相似细胞类型,然后使用 Louvain 社区检测识别联合集群,最后使用最大的数据批次作为参考对因子加载分位数进行归一化,以实现批次校正.
2 方法
本文构建了一个用来校正批次效应的框架,如图1所示,该框架分为3个部分:数据重构模型、生成对抗模型及批次效应分离模型.由于scRNA-seq数据呈现非负的特点,并且其方差大于均值[4],因此考虑使用负二项分布来近似其分布,结合“dropout”事件的影响,出现较多的“假零”,因此考虑使用零膨胀负二项分布(ZINB)来进行数据重构.为了校正批次效应,考虑生成对抗网络的特点,即通过生成器和判别器的对抗使得生成器的输出逼近真实样本.通过将编码器作为生成器,将其潜在层输出作为判别器的输入,分离源批次样本和目标批次样本,通过生成器损失和判别器损失双重优化生成器和判别器,使其达到平衡,即判别器无法区分源批次样本和目标批次样本.将数据传入训练完成的模型,更换批次信息参数,使得目标批次样本向源批次样本空间对齐,完成批次效应校正工作.
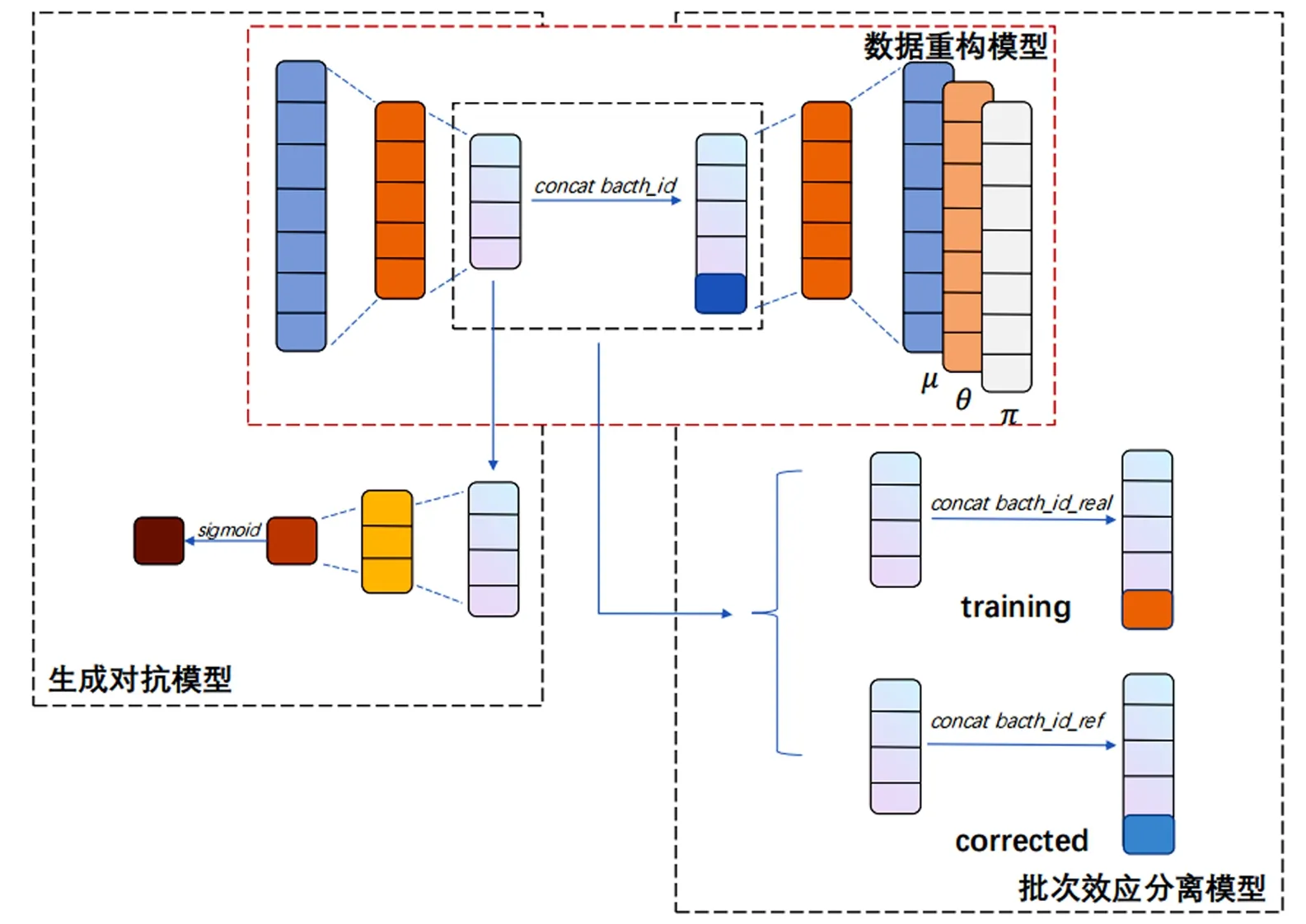
图1 模型框架Fig.1 Framework of scBCMGAN model
2.1 数据重构模型
假设基因表达矩阵为X,其中Xij表示第i个细胞的第j个基因的计数值,结合单细胞测序数据方差大于均值的特点,因此可先假设数据服从负二项分布,则其概率密度函数如式(1)所示:
(1)
其中,μij表示负二项分布的均值,θij表示负二项分布的离散度.考虑到“dropout”事件,用π表示“假零”率来将负二项分布和零膨胀分布结合在一起,可得到零膨胀负二项分布模型[18],如式(2)所示:
(2)
其中,πij为基因j在细胞i中的零膨胀概率,μij为平均表达量参数,θij为离散度参数.公式中的第一行表示第i个样本在第j个基因处的计数为零的概率,该概率可以分解为2个部分:第一部分表示该计数为“假零”的概率;第二部分表示基因表达为真零的概率.公式(2)中的第2行表示x>0的情况,即第i个样本在第j个基因处的计数大于零的概率.
为了估计πij、μij、θij这3个参数,本文采用自编码器进行求解,通过对解码层输出D上添加3个神经元个数相同的非线性层,分别用于估计πij、μij和θij.其中,用sigmoid函数作为激活函数的非线性层用于估计πij,用relu函数作为激活函数的非线性层用于估计μij和θij.具体地,假设第k个非线性层的输出为hk(D),则πij、μij和θij可以分别表示为:
πij=σ(h1(D)),μij=exp(h2(D)),θij=exp(h3(D)),
其中,σ(·)为sigmoid函数,将“dropout”率映射到(0,1)区间内.由于均值和离散度非负,故采用指数函数exp(·)作为激活函数.
最后,本文通过最小化重构误差和ZINB模型的负对数似然函数的加权和来训练自编码器,最大化ZINB模型产生真实观测数据的概率,重构损失如式(3)所示:
(3)
2.2 生成对抗模型
生成对抗网络[20]是一种深度学习模型,由生成器和判别器2个部分组成.生成器的目标是生成逼真的样本,判别器的目标是区分真实样本和生成样本.GAN 的原理是通过2个模型的对抗来训练生成器,使其生成的样本越来越逼真,同时训练判别器,使其能够更好地区分真实样本和生成样本.本文即通过生成对抗的方式使来自不同批次的数据无法被判别器识别来自哪一批次,借此实现校正的目标.
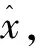
当f(z)越大时,D(z)越接近1,表示输入样本越有可能是源批次数据样本;当f(z)越小时,D(z)越接近0,表示输入样本越有可能是目标批次样本.
在训练过程中,生成器和判别器的目标是相互矛盾的,通过模型的生成对抗训练使得生成器和判别器达到纳什均衡.
判别器的目标是将源批次数据样本和目标批次数据样本识别区分,即最大化以下损失函数:
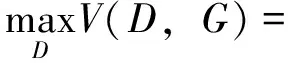
生成器的目标是通过生成重构使得判别器无法区分样本属于哪一批次,即最小化以下损失函数:
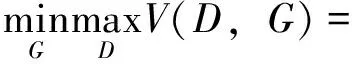
其中,psource(x)表示源批次数据的分布,ptarget(x)表示目标批次数据的分布,x表示一个源批次数据样本,z表示一个目标批次数据样本.V(D,G)表示判别器D和生成器G的价值函数,也被称为最小最大损失函数(minimax loss),即在当前的生成器G的条件下,判别器D的最大期望收益.GAN的训练过程是一个零和博弈的过程,生成器和判别器的优化目标相互矛盾,最终达到了一个纳什均衡状态.
为在网络中进行训练,对于判别器,期望将来自生成器编码得到的数据进行鉴别,将来自源批次的样本使其在判别器中向真实数据标签“1”进行学习,而将来自目标批次的样本使其在判别器中向生成数据标签“0”进行学习,让判别器能够进行判别.如式(4)所示对判别器网络进行损失优化,最大化源批次样本在判别器中的概率,即最小化源批次样本在判别器中的概率的负对数,同时还需最小化目标批次样本在判别器中的概率,通过添加辅助项,最终最小化源批次样本与标签“1”的差异,最小化目标批次样本与标签“0”的差异.对于生成器,将来自目标批次的样本在判别器中向真实数据标签“1”进行学习,让生成器“生成”期望能欺骗判别器的样本.如式(5)所示对生成器网络进行训练,最大化目标批次样本在判别器中的概率,即最小化该概率的负对数,通过添加辅助项,最终为最小化目标批次样本与标签“1”的分布差异.
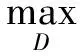
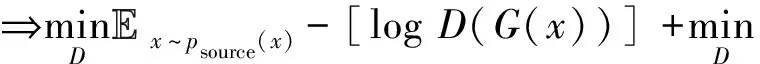
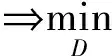
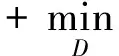
(4)
其中,BCE[21](binary cross entropy)为二元交叉熵,该损失函数将预测值和真实标签视为2个概率分布,并计算它们之间的交叉熵,衡量它们的相似度或差异性.交叉熵越小,表示2个分布越相近.
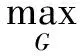
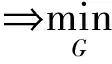
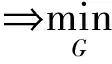
(5)
因此生成器损失LG和判别器损失LD如式(6)所示,在网络优化过程中将最小化该损失,使目标批次样本向源批次样本进行学习分布以及训练判别器学习各样本的来源批次.
LG=∑BCE(D(G(x′)),1),
LD=∑[BCE(D(G(x)),1)+BCE(D(G(x′)),0)].
(6)
整个网络的损失为重构损失与生成器损失及判别器损失之和,即:
L=LZINB+LG+LD.
2.3 批次效应分离模型
当模型训练完成时,此时判别器无法正确识别数据来自哪一批次,对任意样本的理想输出概率为0.5,即对应判别器的期望损失为:
LD=source—loss+target—loss=-log(0.5)+(-log(0.5))=0.693+0.693.
对于目标批次数据,通过生成器的重构使其改变原来明显的批次分布信息,使判别器无法进行正确区分,即对应生成器的期望损失为:
LG=target—loss=-log(0.5)=0.693.
此时整个模型已训练完成,通过ZINB分布约束重构数据与原始数据,为校正批次效应,在潜在层添加的批次信息由原来各个样本对应的批次信息转换成全部为源批次信息,将数据集通过训练完毕的模型进行重构,得到最终校正后的数据.
2.4 算法流程
基于生成对抗网络的scRNA-seq批次效应校正方法的校正过程如算法1所示,在训练之前采用3.2节的方式对数据进行预处理.

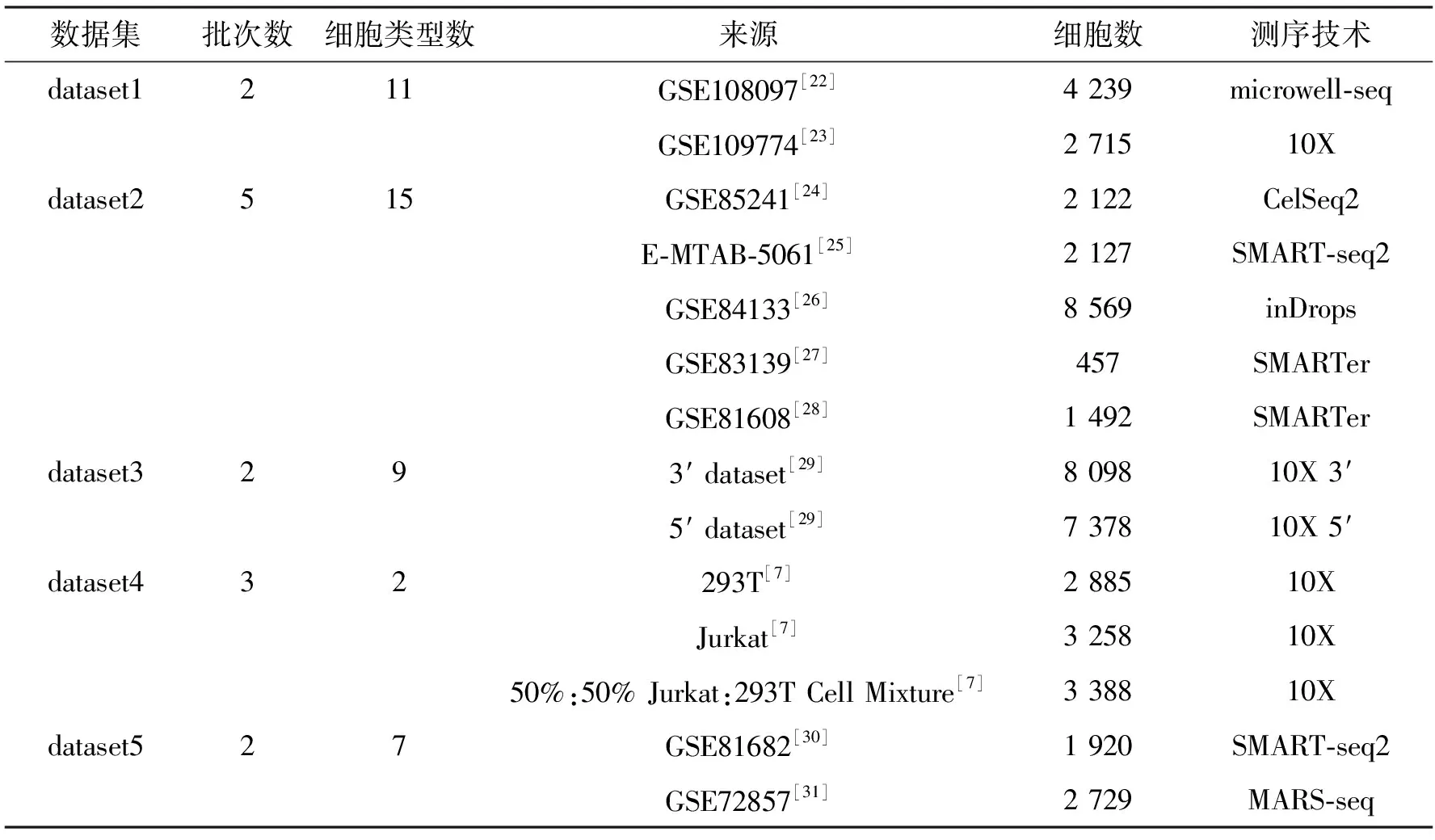
算法1 基于生成对抗网络的scRNA-seq批次效应校正过程输入:数据集X,批次标签信息batchid,训练轮次数epochnum,训练批次数batch,需要更新的所有参数w,生成器网络G(·),判别器网络D(·),获取梯度的函数grad(·),更新参数的函数update(·).输出:校正后的数据集X. 1:初始化网络参数w 2:While epoch 在5个数据集上进行批次效应校正实验,并与其他13种方法以及未经处理的原始数据进行了对比,同时将经由本方法校正后的数据进行可视化分析. 在Tran等[1]整理归纳的5个数据集上进行了实验,分别为Murine Atlas[22-23](dataset1)、Human Pancreas[24-28](dataset2)、Human Peripheral Blood Mononuclear Cell[29](dataset3)、Cell line[7](dataset4)及Mouse Haematopoietic Stem and Progenitor Cells[30-31](dataset5).数据集信息如表1所示. 表1 数据集信息Tab.1 The data information 对来自不同批次的数据进行合并,将少于在5个细胞中表达的基因及少于300个基因表达的细胞进行过滤,对计数矩阵进行归一化处理后再进行log(X+1)处理,然后选择H个高度可变基因.在多批次数据集中,按整个数据集进行归一化处理会混淆批次效应和生物差异,因此,对数据按批次再次进行标准化处理,还原数据在不同批次的潜在效应. 采用的评价指标为平均轮廓系数(average silhouette width)[32],这是一种用于评估聚类结果质量的指标,其定义为每个数据点的轮廓系数(silhouette coefficient)的均值.轮廓系数是一种衡量簇内的稠密程度和簇间的离散程度的指标,其取值范围在-1到1之间,值越大说明簇内差异小,簇间差异大,聚类结果越好,值越小则相反. 对于第i个数据点,其轮廓系数s(i)定义如下: 其中,a(i)表示第i个数据点与其所属簇内其他数据点的平均距离,b(i)表示第i个数据点与其他簇中所有数据点的平均距离的最小值. 对于一个含有n个数据点的聚类结果,ASW的计算公式为: 对于校正后的数据,在批次和细胞亚型2种水平上分别计算ASWbatch和ASWcell—type,ASWbatch越小,说明批次效应越小,ASWcell—type越大,说明同一细胞亚型聚集情况效果越好.为平衡ASWbatch和ASWcell—type,可通过公式(7)计算调和平均值F1score综合评价批次效应校正效果,F1score越大,说明综合批次效应校正效果越好. (7) 本文在5个数据集上进行实验,并与其他13种方法及未校正的原始数据(Raw)进行对比,评价指标为基于ASW的F1score,值越大表示校正效果越显著,结果如表2所示. 表2 实验结果比较Tab.2 Comparison of experiment results 实验结果显示,scBCMGAN在实验的各个数据集上均有一定的优势,尤其是在dataset1、dataset3、dataset4、dataset5这4个数据集上有显著优势,优于其他方法.为更加直观地说明各方法的表现差异,本文计算了各方法在5个数据集上的秩次和.实验结果表明本文方法的秩次和为10,次优方法为Harmony,且这2种方法的综合表现与其他方法相比有明显优势,并且与原始数据集的效果表现进行对比可以进一步说明批次效应校正的重要性以及本文方法的可行性和有效性.与此同时,在含5个批次的dataset2上,scBCMGAN表现为中上水平,说明面对多批次数据时,本文方法没能十分有效地一次性将其余目标批次向源批次进行参考校正. UMAP[33](uniform manifold approximation and projection)是一种非线性降维技术,用于将高维数据降到低维空间进行可视化和分析.UMAP利用流形假设,即在高维空间中的大多数数据点都分布在一个低维流形上,该算法首先通过一些距离度量(例如欧几里得距离、闵可夫斯基距离等)计算数据点之间的相似度,然后使用随机梯度下降等优化方法将数据点映射到低维空间.在映射过程中,UMAP使用一些技术(例如随机游走和最小生成树)来保留数据之间的局部结构和聚类,同时尽可能地减少全局误差.UMAP的可视化效果通常比其他降维技术更好,因为它能够更好地保留数据之间的局部结构和聚类,并且能够在保持数据点的全局一致性的同时提供更高的可解释性. 本文方法结合UMAP进行可视化分析,如图2所示,左图展示了各个细胞的批次聚集程度,右图展示了各个细胞的细胞亚型聚集程度.批次聚集程度表示不同批次的细胞在UMAP中的聚集情况,如果批次效应没有被校正,不同批次的细胞可能会在UMAP中聚集成不同的区域.细胞亚型聚集程度则表示细胞在UMAP中的聚类情况,可以用来评价聚类的效果.在批次效应校正UMAP效果图中,通过降低批次聚集程度、尽可能维持细胞亚型聚集的方式,可以展示批次效应校正的效果,即展示批次效应校正后细胞在UMAP中的分布情况和聚类结果.如果批次效应校正效果越好,说明不同批次的细胞在UMAP中的聚集越少,细胞亚型聚集效果越好.本文方法在各个数据集上均展现了优良的校正效果,将来自不同批次的样本数据根据其本身固有的生物学潜在特征对批次效应进行了校正,使得同一细胞亚型的数据尽可能跨批次聚集,将不同批次的细胞进行校正,使得细胞的表达模式更加一致,从而更好地反映细胞本身的特征.如图2(d)所示,293t和jurkat 2种细胞亚型在批次3中均有存在,实验结果显示本文方法较好地将这2种细胞按其类型进行了跨越批次的聚集,大大降低了批次效应的影响. 图2 UMAP可视化效果图Fig.2 The result of UMAP visualization 针对dataset5,所有方法校正后对应的1-ASWbatch和ASWcell—type如表3所示.该数据集由2个批次构成,共有7种细胞亚型,但其中有一批次仅含3种细胞亚型,实验结果表明,尽管生成对抗网络对无参考批次的数据难以进行学习,但本文方法也能在综合考虑批次效应和保留细胞亚型聚集的基础上将不同批次的数据分离出细胞亚型,而对比的其他方法有些是以牺牲细胞亚型聚集进而降低批次效应,但这会为下游分析如聚类等带来困难. 表3 dataset5实验结果比较Tab.3 Comparison of experiment results on dataset5 本文提出了一种基于生成对抗网络的批次效应校正算法,结合自编码器对潜在层表示进行批次效应校正,通过零膨胀负二项分布对数据重构进行约束,最后将训练完成的模型转换批次标签完成批次效应校正.实验结果表明,本文所提出的方法在各个真实数据集上均有较好的性能,尤其是在4个数据集上展现了显著的优势,并且校正过程是在基因水平上进行的,因此校正后的数据能够用于下游分析. 对于多批次数据和批次间细胞亚型不均衡数据,生成对抗网络较难学习数据表示,为此下一步将重点考虑针对此类数据进行校正,通过添加合适的约束进一步优化网络结构. 本文代码地址:https:∥gitee.com/cdclx/sc-bcmgan.3 实验
3.1 数据说明
3.2 数据预处理
3.3 评价指标
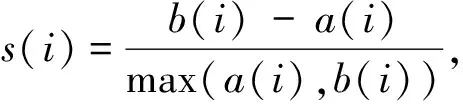
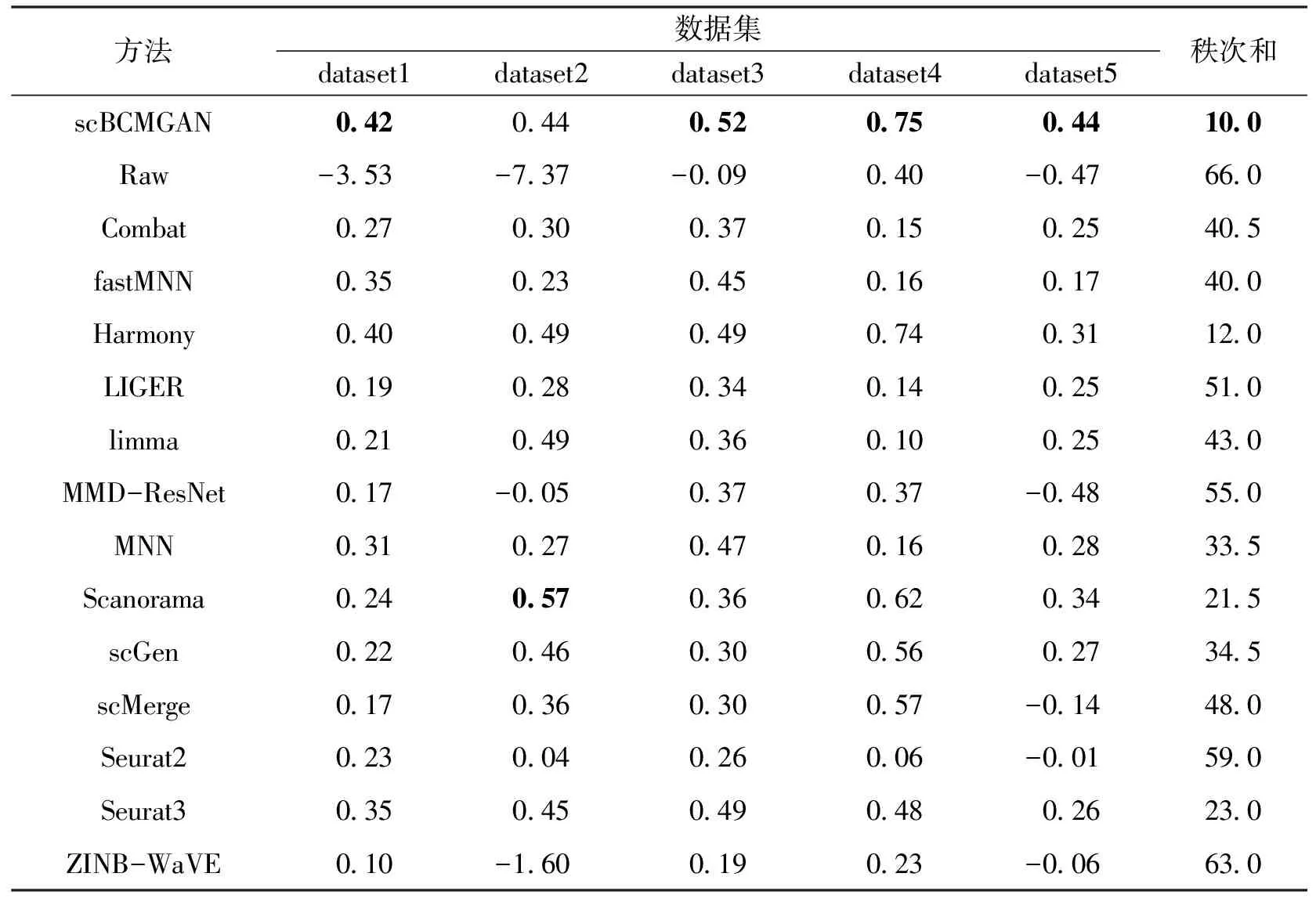
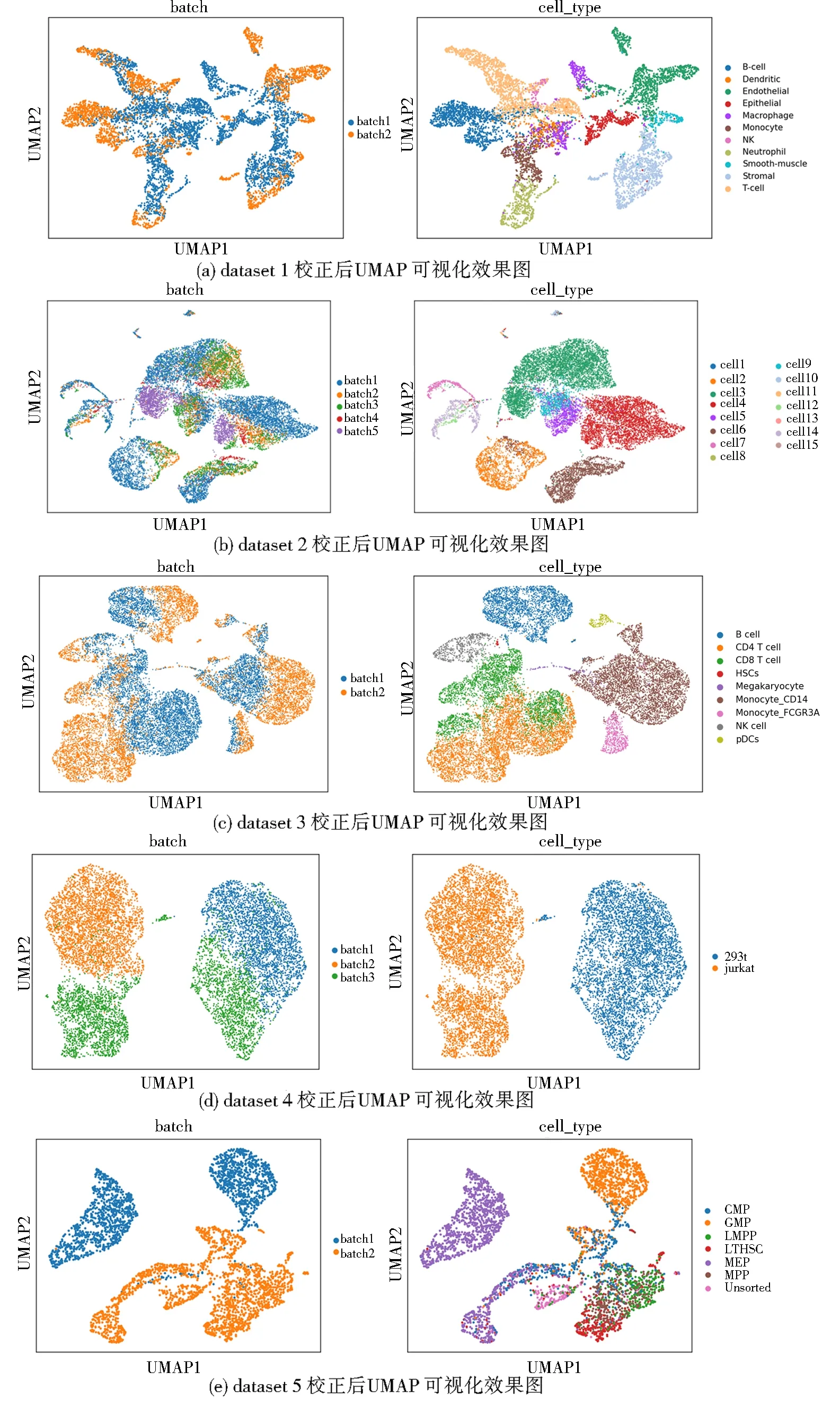
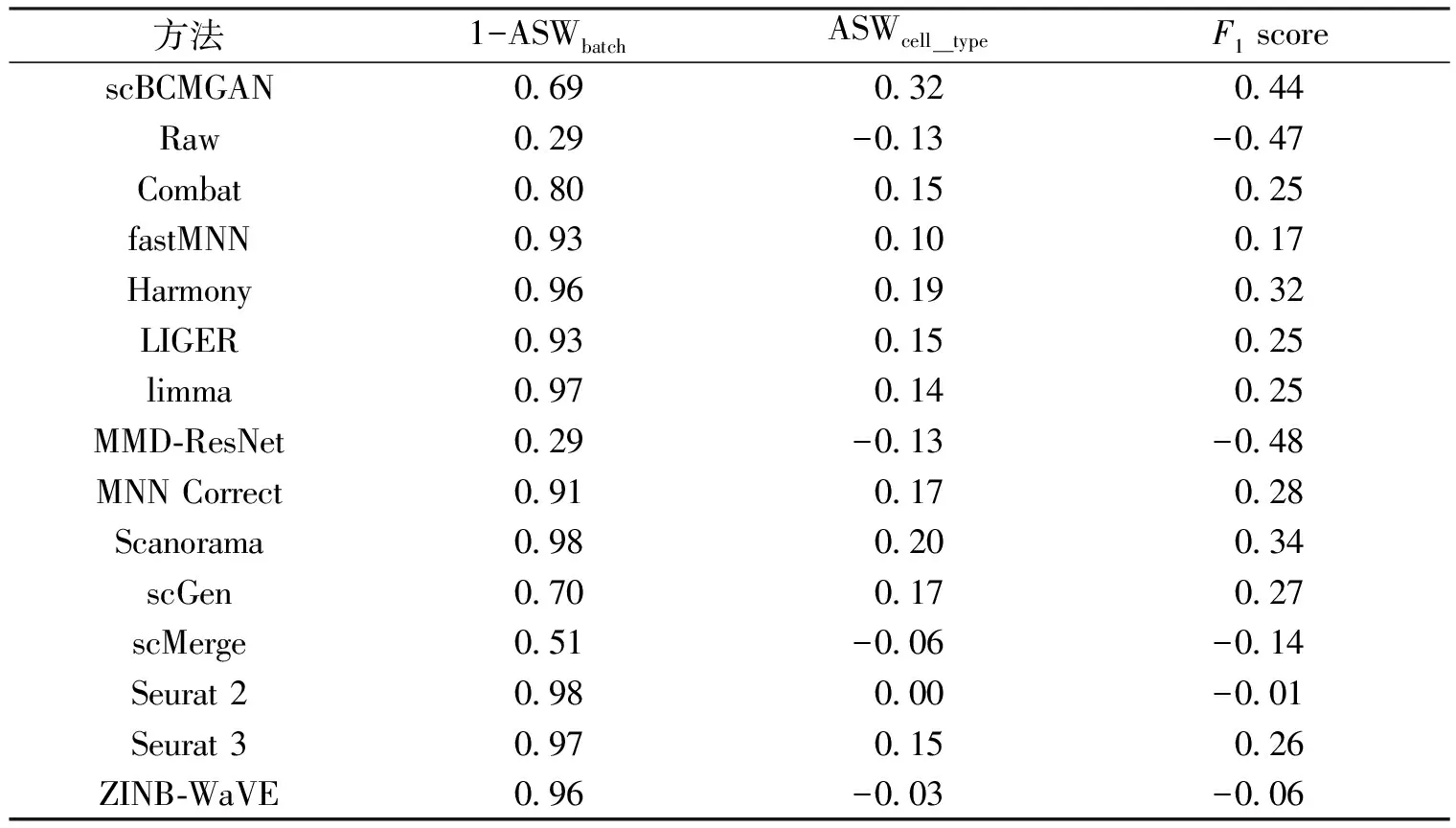
3.4 实验结果
4 总结与展望
