考虑材料厚度的空间充气舱柔性防护结构折叠方案设计
2023-11-10徐彦房冠辉贾贺
徐彦 房冠辉 贾贺
考虑材料厚度的空间充气舱柔性防护结构折叠方案设计
徐彦1房冠辉2,3贾贺2,3
(1浙江大学航空航天学院,杭州 310027)(2北京空间机电研究所,北京 100094)(3 中国航天科技集团有限公司航天进入、减速与着陆技术实验室,北京 100094)
充气式太空舱可应用于建设载人空间站,但是其柔性防护结构的折叠方案设计方法很少被研究。文章基于非线性有限元法分析了层合薄膜材料中各单层薄膜的折叠过程,得到折叠应力/应变和折叠角度之间的关系曲线;建立了柔性防护结构折叠性能分析模型,得到了柔性防护结构的最小折叠半径和折叠应力分布等。针对类似于毕格罗可充气活动模块(Bigelow Expandable Activity Module,BEAM)的空间充气舱柔性防护结构,采用波纹管折叠样式设计了折叠方案,并评估了体积折叠率。柔性防护结构的折叠方案设计可以为未来空间充气舱的研制和应用提供支撑。
空间充气舱 柔性防护结构 折叠性能 折叠方案设计
0 引言
为了建设载人空间站或者月球/火星基地,美国、欧空局、俄罗斯等都广泛开展了空间充气舱结构技术研究,如NASA的往返居住舱(Transit Habitation,TransHab)[1-2]、充气月球基地[3]、InFlex月球舱[4]、欧洲的月球村计划[5]、俄罗斯的月球综合探索与开发计划[6]和我国的国际月球科考站计划[7]等。2016年国际空间站上的毕格罗可充气活动模块(Bigelow Expandable Activity Module,BEAM)圆满完成充气展开试验,标志着空间充气舱已经成功应用于载人空间站。为了实现空间充气舱的防热和防空间碎片撞击设计,由层合薄膜材料构成的柔性防护结构技术受到广泛关注[8-9]。柔性热防护结构一般由层合薄膜材料构成,包括防热层、隔热层、空间碎片防护层、承压层和阻气层等多个功能层,而每个功能层又由多层薄膜组成,厚度一般在厘米级。空间充气舱搭载发射之前,柔性防护结构需要折叠包装,在轨充气展开形成预先设计的结构。柔性防护结构的折叠理论和折叠性能评估直接决定了空间充气舱能否顺利搭载、在轨展开进而影响整个航天任务的成败。如国际空间站上的BEAM空间充气舱,在第一次充气展开试验中就没有按预定计划展开。
空间充气舱的几何外形设计为圆柱状或圆锥状,三维圆柱状或圆锥状结构的折叠理论主要有:Z字形折叠、卷曲折叠、折纸折叠、变直径伸缩式折叠等[10-11]。折纸折叠理论又有:Yoshimura样式、波纹管样式、Miura样式、六折线样式、刚性折纸样式[12-14]。采用不同的折叠理论,折叠方向、折叠效率、折叠应力分布、展开稳定性、通气性等折叠性能各不相同。其中一些折叠理论被试验验证,并得到了广泛的工程应用,但目前三维筒状结构的折叠理论中还很少考虑薄膜材料有限厚度的影响。传统的折叠理论较少考虑有限厚度的影响,而柔性防护结构中层合材料的厚度不可忽略,有必要考虑其对折叠方案设计的影响。层合材料有限厚度的影响主要体现在:①折叠方案中折叠单元的重复性差;②由于不均匀的折叠方案导致折叠包装体积大;③折叠后柔性材料中存在拉/压应力[15]。近年来已经发展出一些考虑厚度的一维折叠理论[16-18],但是这些折叠理论或者需要层合材料的变厚度设计,或者设计有铰链或缝隙导致薄膜材料不连续,无法应用于空间充气舱的折叠方案设计。
柔性层合材料的折叠性能表征主要集中于单一折痕附近的折叠性能分析与试验验证[19-21]。对于柔性层合材料在折痕附近的折叠性能,可以建立纯弯悬臂梁模型,考虑几何非线性和材料非线性,得到弯矩和角度之间的曲线和折痕附近的应力分布,进而确定折痕附近的折叠弯曲刚度[22]。这些研究大多针对聚合物薄膜[23]或铝-聚合物层合薄膜,柔性防护结构中有限厚度的层合材料折叠性能研究还很少涉及。本文在分析单层薄膜折叠过程的基础上,研究了有限厚度的柔性防护结构的折叠性能,并考虑材料厚度的影响设计了一类典型空间充气舱的折叠方案。
1 折叠方案设计方法
1.1 材料组成及参数
大型载人空间充气舱的柔性防护结构为柔性层合材料,从空间充气舱的外表面向内一共由五层构成:隔热层、空间碎片及辐射防护层、约束层、承压层及内部防磨损层等[2]。每个功能层的材料名称、层数和厚度见表1。
表1 功能层的材料名称、层数和厚度
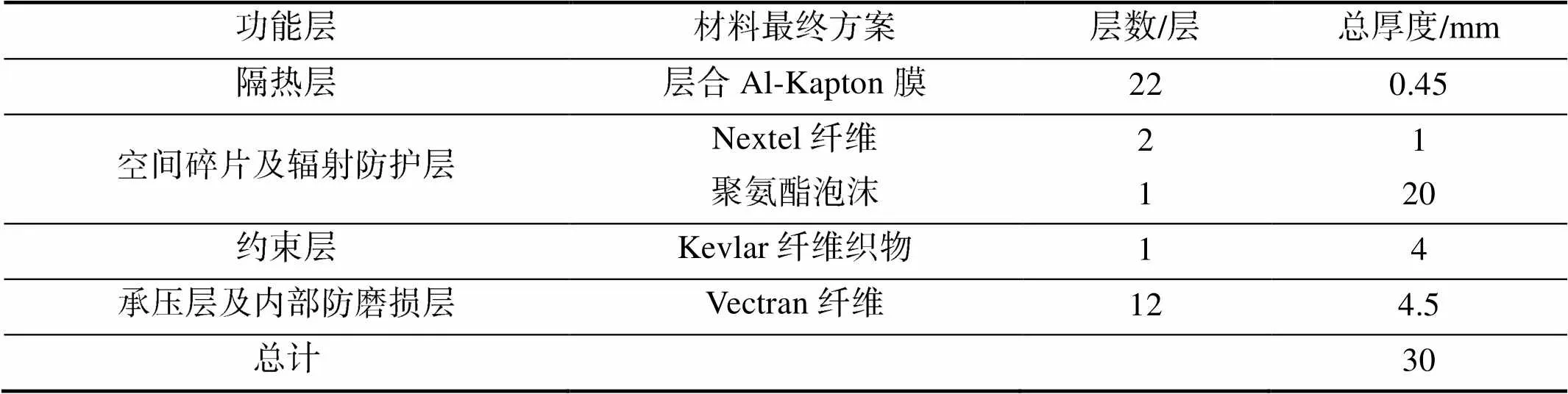
Tab.1 Material, number of layers and thickness of functional layers
确定各功能层材料的工程参数[22-23],如表2所示,包括密度、弹性模量、泊松比和安全强度。柔性防护结构折叠性能分析中,需要根据折叠应力/应变进行强度判别,选用的强度判别准则为:隔热层的层合Al-Kapton薄膜采用最大应变准则,安全强度为薄膜的最大伸长线应变除以安全系数1.5;其他功能层采用最大应力准则,安全强度为极限抗拉强度除以安全系数1.5,具体数值见表2。
表2 各功能层材料的工程参数

Tab.2 Engineering parameters of each functional layer material
1.2 折叠方案设计流程
在确定柔性防护结构材料方案的基础上,折叠方案的设计流程如图1所示。首先针对柔性层合材料中的各个单层薄膜,进行折叠过程的准静态建模和折叠性能分析,得到折叠应力和折痕处曲率半径的关系曲线。然后进行柔性防护结构的折叠状态初步设计,由各单层薄膜的折叠应力-曲率半径的关系曲线确定正向折叠和反向折叠的最小曲率半径。接着分别完成两向折叠过程的折叠过程建模及分析,得到折痕处最小曲率半径及折叠应力分布情况,进而确定折痕影响范围。最后根据空间充气舱的几何外形和尺寸,协同设计折叠数、两向折叠的最小曲率半径等参数,完成空间充气舱的折叠方案设计。迭代设计得到的最终折叠方案,需满足以下两个设计要求:1)折痕处材料的安全系数优于1.5;2)体积折叠率优于4。
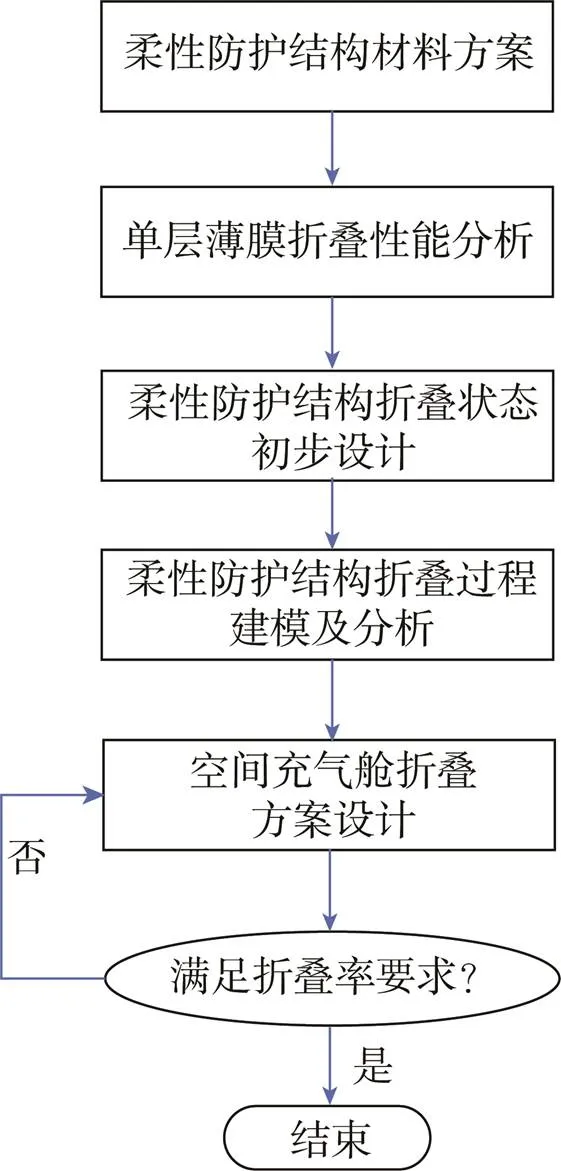
图1 折叠方案设计流程
2 单层薄膜折叠性能分析
2.1 准静态折叠过程建模
采用有限元软件,分别建立各单层薄膜的几何模型,为3 m×1 m的矩形,见图2(a),中间有一个预留折痕区域(图中分别由三条红色线确定区域的边界和中线),方便后续设置载荷和测量折痕处最小曲率半径。矩形薄膜采用S4R单元离散,中间预留折痕区域的网格适当加密,如图2(b)所示。
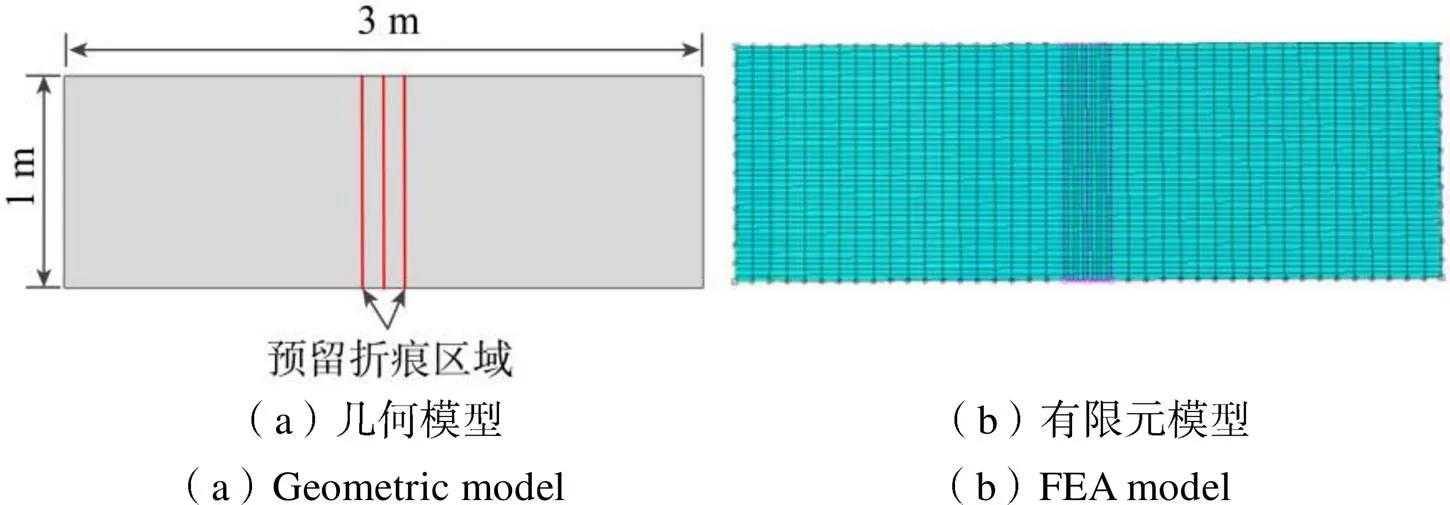
图2 单层薄膜的分析模型
根据表2的材料工程参数,分别设置单层薄膜的密度、弹性模量和泊松比。根据表1,分别设置单层薄膜的厚度。设置分析类型为静力通用分析步,打开大变形的设置。设置预留折痕区域的中线位置约束、、三个方向的位移,折痕两侧的面域施加绕折痕旋转90°的位移载荷,两侧的面域相向弯折,如图3所示。

图3 边界条件及载荷设置
2.2 折叠性能分析结果
通过对厚度为0.45 mm的层合Al-Kapton膜折叠过程进行准静态分析,得到隔热层折叠后的最大应变为0.007 1,远小于安全强度0.09,折痕影响区域仅限于预留折痕区域,其他区域的折叠应变很小,如图4所示。按照最大应变准则可判定折叠完成后,隔热层的层合Al-Kapton膜是安全的。

图4 隔热层的折叠应变分布
改变材料属性和厚度可重复分析其他单层薄膜的折叠过程,从而得到了各层的应力/应变随曲率半径的变化情况,如图5所示。由各单层薄膜的折叠应力/应变-曲率半径曲线可知,随着折痕处曲率半径的变小,折叠应力/应变迅速变大,Nextel纤维层在曲率半径较大时最大应力就超过安全强度,而其他四层薄膜能够弯折到很小曲率半径时折叠应力/应变才会超过安全强度。后续柔性防护结构折叠状态初步设计中,将由Nextel纤维层控制柔性防护结构能达到的最小折叠曲率半径。
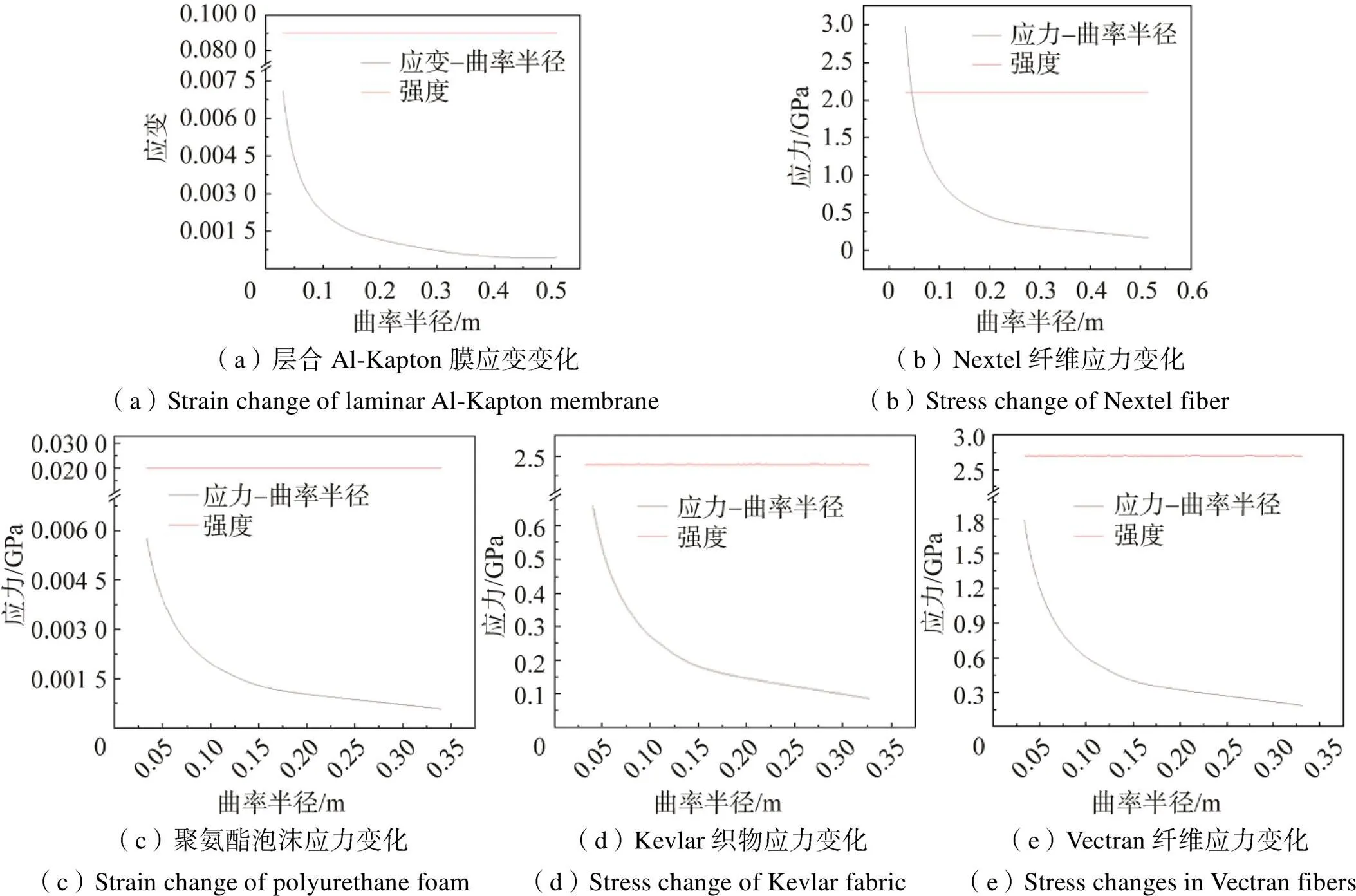
图5 折叠应力/应变-曲率半径曲线
3 柔性防护结构折叠性能分析
3.1 折叠状态初步设计
在折叠方案中折痕有峰线和谷线,所以柔性防护结构存在正向折叠和反向折叠两种情况,见图6。根据各单层薄膜的折叠应力/应变-曲率半径曲线及表1的铺层方案,进行柔性防护结构折叠状态的初步设计。首先根据图5中的Nextel纤维层的折叠应力/应变-曲率半径曲线确定其合适的曲率半径,然后按照各单层薄膜的厚度依次确定其他四层薄膜的曲率半径,得到的折叠状态初步结果如表3和表4所示。同时按图5的折叠应力/应变-曲率半径曲线进行插值,得到对应的各单层薄膜最大折叠应变或应力,按照强度判别准则可知各单层薄膜都满足强度要求:隔热层的层合Al-Kapton薄膜采用最大应变准则,最大折叠应变小于应变表示的安全强度;其他功能层采用最大应力准则,最大折叠应力小于应力表示的安全强度。柔性防护结构正向折叠后的折痕处厚度为119.8 mm,反向折叠后的折痕处厚度为155.1 mm,如图6。
表3 正向折叠设计

Tab.3 Forward folding design
表4 反向折叠设计

Tab.4 Reverse folding design
3.2 折叠过程建模及分析
柔性防护结构折叠过程建模和2.1节中的单层薄膜类似,柔性防护结构模型由多层矩形壳构成,如图7。将不同的层按照表1的顺序进行铺层,相邻层之间按照薄膜的厚度设置初始间隙。由于在折叠加载过程中,相邻层之间会发生接触,需要设置相互作用。模型中设置了相邻层之间无摩擦的硬接触对,以防止网格穿透。同样地,设置分析类型为静力通用分析步,打开大变形的设置。对于分析正向折叠过程,设置层合Al-Kapton膜这层平面壳的预留折痕区域的中线位置约束、、三个方向的位移,折痕两侧的面域施加绕折痕旋转90°的位移载荷,两侧的面域相向弯折。对于分析反向折叠过程,设置Vectran纤维这层平面壳的预留折痕区域的中线位置约束、、三个方向的位移,折痕两侧的面域施加绕折痕旋转90°的位移载荷,两侧的面域相向弯折。

图7 柔性防护结构折叠过程建模
分析正向折叠过程和反向折叠过程,得到柔性防护结构各单层薄膜中的折叠应力/应变分布及折痕影响范围,见图8和图9。由折叠应力/应变分布云图可知,各单层薄膜的最大折叠应力/应变数值分析结果与表3和表4中的结果非常接近,最大应力/应变出现在折痕附近,远离折痕的区域应力/应变很小,故折叠过程只对折痕附近有影响。

图8 正向折叠的折叠应力/应变
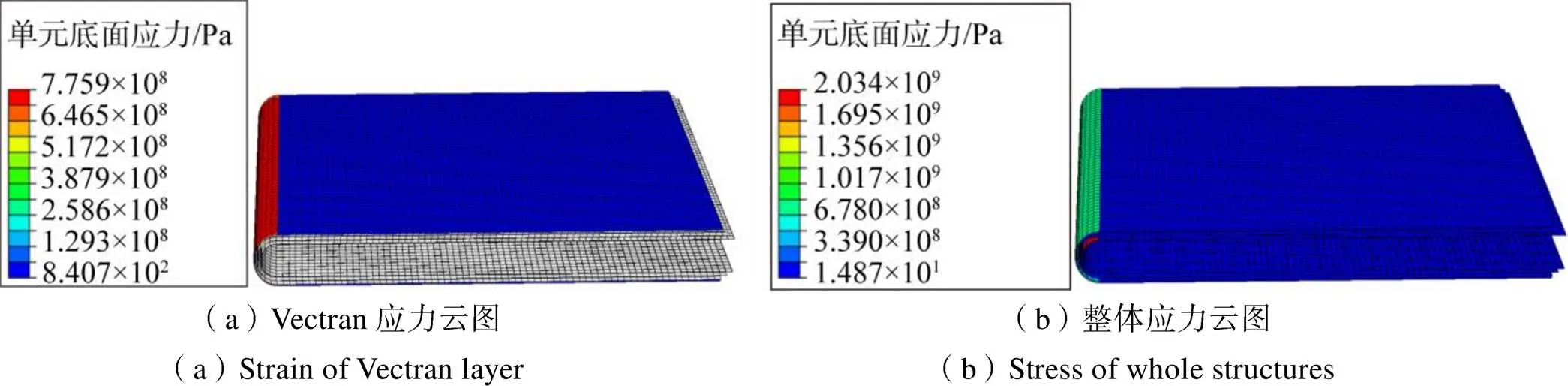
图9 反向折叠的折叠应力/应变
4 类BEAM空间充气舱折叠方案设计
4.1 几何尺寸
本文将针对类BEAM空间充气舱,按照表1的柔性防护结构设计其折叠方案。国际空间站上的BEAM空间充气舱,折叠状态舱体直径2.36 m,长度2.16 m,体积3.6 m3,展开后舱体近似为直径3.2 m,长度4.0 m,可提供16 m3的舱内容积。类BEAM空间充气舱完全展开状态的外形类似纺锤形,如图10(a)。剖面的几何尺寸如图10(b)所示,最大截面处直径为3.2 m,长度为4.0 m,和其他舱对接的舱门直径为1.44 m,侧壁由两段半径为3.39 m的圆弧构成。

图10 类BEAM空间充气舱几何尺寸
4.2 折叠方案设计及评估
采用波纹管折叠方案,根据前述柔性防护结构的折叠性能分析结果,确定正向折痕和反向折痕处的中性面折叠曲率半径均为0.065 m,见图11。此时各层薄膜折痕处的最大折叠应变或应力均小于安全强度。
确定了折痕处的折叠曲率半径后,按照类BEAM空间充气舱的完全展开状态几何尺寸和体积折叠率的设计要求,优化设计折痕布局和相关折叠参数,最终设计得到折叠方案,如图12所示。空间充气舱的侧壁为旋转曲面,如图12(a)虚线所示的母线分为不等长度的8段,故折叠方案中一共有8条环状的折痕。柔性防护结构可通过不同直径的刚性圆环向下压或向上提实现折叠过程,刚性圆环如图12(a)中的小圆圈,刚性圆环向下压或向上提按箭头所示。空间充气舱折叠状态的三维模型如图12(b)。折叠后充气舱可以包络在Φ3.2 m×0.95 m的圆柱体中,体积折叠率为4.2,接近于BEAM空间充气舱。但是由于柔性防护结构采用波纹管折叠方案,只能进行长度方向的折叠,而截面方向无法进行折叠。

图11 两类折痕的曲率半径

图12 空间充气舱的折叠方案
5 结束语
本文数值分析了柔性防护结构及其各单层薄膜的折叠过程,探究了考虑厚度的柔性防护结构的最小折叠半径和折叠应力分布,设计了类BEAM空间充气舱的折叠方案,得到以下结论:
1)各单层薄膜随着折痕处曲率半径的变小,折叠应力/应变迅速变大。柔性防护结构折叠状态初步设计中,由Nextel纤维层控制柔性防护结构能达到的最小折叠曲率半径。
2)厚度30 mm的柔性防护结构,正向折叠后的折痕处厚度为119.8 mm,反向折叠后的折痕处厚度为155.1 mm。最大应力/应变出现在折痕附近,远离折痕的区域应力/应变很小,故折叠过程影响区域仅限于折痕附近。
3)考虑柔性防护结构厚度后,类BEAM空间充气舱折叠方案中,正向折痕和反向折痕处的中性面折叠曲率半径确定为0.065 m,各层薄膜的最大折叠应变或应力均小于安全强度,体积折叠率为4.2,接近于BEAM空间充气舱。
考虑材料厚度的柔性防护结构折叠性能研究和折叠方案设计可以为未来空间充气舱的研制和应用提供支撑,也可用于充气展开机翼的折叠设计和工程研制。
[1] BELVIN W K, WATSON J J, SINGHAL S N. Structural Concepts and Materials for Lunar Exploration Habitats[C]//AIAA Space 2006 Conference and Exposition,September 19-21, 2006, San Jose, CA, USA.
[2] BADHWAR G D, HUFF H, WILKINS R. Comparison of Graphite, Aluminum, and TransHab Shielding Material Characteristics in a High-energy Neutron Field[J]. Radiation Measurements, 2002, 35(6): 545-549.
[3] HINKLE J, DIXIT A, LIN J K, et al. Design Development and Testing for an Expandable Lunar Habitat[C]//AIAA Space 2008 Conference & Exposition, September 9-11, 2008, San Diego, California, USA.
[4] CRUSAN J, GALICA C, GILL T. NASA’s Exploration Systems and Habitation (X-Hab) Academic Innovation Challenge[J]. Acta Astronautica, 2018, 151: 412-419.
[5] 松堂. 没有实现的美欧月球站设想[J]. 太空探索, 2021(6): 42-44. SONG Tang. The Idea of a US-European Lunar Station did not Come to Fruition[J]. Space Exploration, 2021(6): 42-44. (in Chinese)
[6] 范唯唯, 杨帆, 韩淋, 等. 俄罗斯未来月球探索与开发计划解析[J]. 科技导报, 2019, 37(16): 6-11. FAN Weiwei, YANG Fan, HAN Lin, et al. Overview of Russia's Future Plan of Lunar Exploration[J]. Science & Technology Review, 2019, 37(16): 6-11. (in Chinese)
[7] 裴照宇, 刘继忠, 王倩, 等. 月球探测进展与国际月球科研站[J]. 科学通报, 2020, 65(24): 2577-2586. PEI Zhaoyu, LIU Jizhong, WANG Qian, et al. Overview of Lunar Exploration and International Lunar Research Station[J]. Chinese Science Bulletin, 2020, 65(24): 2577-2586. (in Chinese)
[8] 徐彦, 郑耀, 匡松松, 等. 展开式月球基地热防护结构方案研究, 深空探测学报, 2016, 3(2): 168-174. XU Yan, ZHENG Yao, KUANG Songsong, et al. Conceptual Design of Flexible Thermal Protect Structure for Deployable Lunar Habitats[J]. Journal of Deep Space Exploration, 2016, 3(2): 168-174. (in Chinese)
[9] HONG Y, YAO W, XU Y. Structural Design and Impact Analysis of Deployable Habitat Modules[J]. International Journal of Aerospace Engineering, 2018, 3252104: 1-15.
[10] XU Y, ZHENG Y, GUAN F, et al. Parametric Model Method and Deployment Simulation of Inflatable Antenna Structures[J]. Journal of Aerospace Technology and Management, 2015, 7(2): 219-230.
[11] HONG Y, YAO W, XU Y. Research on the Folding Patterns and Deployment Dynamics of Inflatable Capsule Structures[J]. Journal of Aerospace Technology and Management, 2018, 10(1): 1-12.
[12] SCHENK M, VIQUERAT A D, SEFFEN K A, et al. Review of Inflatable Booms for Deployable Space Structures: Packing and Rigidization[J]. Journal of Spacecraft and Rockets, 2014, 51(3): 762-778.
[13] SCHENK M, KERR S G, SMYTH A M, et al. Inflatable Cylinders for Deployable Space Structures[C]// Proceedings of the 1st International Conference Transformables, September 18-20, 2013, Seville, Spain.
[14] XU Y, Fang Q, LI H. Kinematic and Quasi-static Analysis Model of a Novel Variable Stiffness Pneumatic Artificial Muscle[J]. Sensors and Actuators A: Physical, 2021, 329(12): 1-11.
[15] SAKAMOTO H, NATORI M C, KADONISHI S. Folding Patterns of Planar Gossamer Space Structures Consisting of Membranes and Booms[J]. Acta Astronautica, 2014, 94(1): 34-41.
[16] EDMONDSON B J, LANG R J, MAGLEBY S P, et al. An Offset Panel Technique for Thick Rigidly Foldable Origami[C]//Proceedings of the ASME 2014 International Design Engineering Technical Conferences, August 17-20, 2014, Buffalo, New York, USA.
[17] Sakamoto H, Natori M C, Kadonishi S. Folding Patterns of Planar Gossamer Space Structures Consisting of Membranes and Booms[J]. Acta Astronautica, 2014, 94(1): 34-41.
[18] Arya M, Lee N, Pellegrino S. Crease-free Biaxial Packaging of Thick Membranes with Slipping Folds[J]. International Journal of Solids and Structures, 2017, 108: 24-39.
[19] 王友善, 谢志民, 杜星文. 柔性复合薄膜折叠损伤实验研究[J]. 哈尔滨工业大学学报. 2006, 38(8): 1292-1294. WANG Youshan, XIE Zhimin, DU Xingwen. Experimental Investigation of the Folding Damage of the Flexible Composite Membranes[J]. Journal of Harbin Institute of Technology, 2006, 38(8): 1292-1294. (in Chinese)
[20] GABRIEL S, ANDREW V, GUGLIELMO S A. A Model of Packaging Folds in Thin Metal-olymer Laminates[J]. Journal of Applied Mechanics, 2017, 84(10): 1-11.
[21] 蔡祈耀, 陈务军, 张大旭, 等. Kapton薄膜折叠力学行为分析与试验[J]. 上海交通大学学报, 2014, 48(8): 1109-1115. CAI Qiyao, CHEN Wujun, ZHANG Daxu, et al. Mechanical Behavior Analysis and Experiment of Kapton Film Folding[J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1109-1115. (in Chinese)
[22] 林国昌, 万志敏, 杜星文. Al-Kapton层合薄膜力学行为的实验研究. 材料科学与工艺, 2006, 14(3): 261-264. LING Guochang, WAN Zhimin, DU Xingwen. Experimental Research on the Mechanical Behavior of Aluminum Laminate[J]. Materials Science & Technology, 2006, 14(3): 261-264. (in Chinese)
[23] 廖惠东, 钟利萍, 刘杰, 等. Vectran材料的抗拉性能仿真与验证. 计算机仿真, 2016, 33(2): 413-417. LIAO Huidong, ZHONG Liping, LIU Jie, et al. Simulation and Verification of Tensile Properties of Vectran Material[J]. Computer Simulation, 2016, 33(2): 413-417. (in Chinese)
Folding Pattern Design of Flexible Protective Structures of Space Inflatable Habitat Considering Material Thickness
XU Yan1FANG Guanhui2,3JIA He2,3
(1 School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China)(2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(3 Laboratory of Aerospace Entry, Descent and Landing Technology, CASC, Beijing 100094, China)
Inflatable space habitat can be applied in the construction of manned space station, but the folding pattern design method of its flexible protective structures is rarely researched. Based on the nonlinear finite element method, the folding process of each single membrane in laminated membrane materials is analyzed. The relation curves of folding stress/strain and folding angle are obtained. The folding performances analysis model of the flexible protective structure is established. The minimum folding radius and folding stress of the flexible protective structure are obtained. For the flexible protective structure of a space inflatable habitat which is similar to Bigelow Expandable Activity Module (BEAM), the folding pattern is designed based on bellows folding pattern, and the volume folding rate is evaluated. Folding pattern design of flexible protective structures provides support for the future development and application of space inflatable habitat.
inflatable space habitat; flexible protective structure; folding performances; folding pattern design
V474
A
1009-8518(2023)05-0011-09
10.3969/j.issn.1009-8518.2023.05.002
徐彦,男,1982年生,2009年获浙江大学土木工程专业博士学位,现为浙江大学航空航天学院副教授、博导。主要研究方向为航天器结构机构、空间机器人。E-mail:xyzs@zju.edu.cn。
2022-11-14
国家自然科学基金(91748209,11402229)
徐彦, 房冠辉, 贾贺. 考虑材料厚度的空间充气舱柔性防护结构折叠方案设计[J]. 航天返回与遥感, 2023, 44(5): 11-19.
XU Yan, FANG Guanhui, JIA He. Folding Pattern Design of Flexible Protective Structures of Space Inflatable Habitat Considering Material Thickness[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(5): 11-19. (in Chinese)
(编辑:陈艳霞)
