U 形渠道量水槽收缩比确定方法研究

2023-11-10戚玉彬

人民黄河 2023年11期

戚玉彬

（伊犁职业技术学院，新疆伊宁 835000）

收缩比是保证量水槽出现临界流的关键参数。量水槽在选型时，要先确定收缩比才能得到量水槽的尺寸。如何确定收缩比是制约各类U 形渠道量水槽在灌区推广应用的技术难题。吕宏兴等［1］通过对机翼形量水槽的研究，从弗劳德数的角度提出比降较小的渠道应取较大的收缩比。何武全等［2］以测流误差小于5%和壅水高度不大于10 cm 为条件，通过试验得到圆柱体收缩比的范围。刘英等［3］、刘嘉美等［4］分别以壅水高度不超过5、10 cm 为参考，得到圆头量水柱适宜收缩比的范围。蒋沛等［5］通过对半圆柱形量水槽进行数值模拟表明，为不影响U 形渠道的过流能力，应选择较大的收缩比。王玉宝等［6］以上游壅水高度不超过10 cm 为标准，认为当渠道比降小于1／1 000和1／500 时，收缩比应大于0.51 和0.61。戚玉彬等［7］通过田间试验比较量水槽性能的优劣，给出了陡坡U形渠道量水槽的适宜收缩比。以上研究是从壅水高度的角度得到收缩比的范围，受试验所选收缩比个数的限制，并不能准确界定收缩比的范围。抛物线形喉口式量水槽［8－9］和直壁式量水槽［10］根据渠道断面参数和渠道比降来确定收缩比，但未考虑渠道流量因素对收缩比的影响。国外学者侧重于对圆柱槽［11－12］、半圆柱槽［13－14］、中央挡板槽［15－17］和无喉槽［18－19］等流量公式的研究，对U 形渠道量水槽收缩比的研究甚少。以低弗劳德数或低壅水高度为标准确定收缩比，往往导致壅水高度过大或无法形成自由出流，均具有一定的局限性，收缩比的确定应综合考虑弗劳德数和壅水高度的影响。喉口宽度是影响弗劳德数和壅水高度的重要因素之一，若建立喉口宽度与弗劳德数、壅水高度之间的定量关系，再利用弗劳德数、壅水高度的应用限制条件，即可对收缩比进行确定。笔者以一种U 形渠道三角形量水槽为研究对象，通过理论分析和田间试验，对弗劳德数和壅水高度的影响因素进行定性分析，建立包含喉口宽度的弗劳德数和壅水高度的经验公式，以期界定收缩比的范围和确定适宜的收缩比。

1 试验与方法

1.1 三角形量水槽的结构

三角形量水槽是在矩形无喉段量水槽的基础上简化而来的，主要改进有两处：一是将上游进口段和下游出口段的不同折角改为相同折角，折角大小根据渠道实际情况在1 ∶（1～2.5）范围内选择；二是去除矩形无喉段量水槽的水平槽底，直接沿用原U 形渠道渠底。三角形量水槽的上游进口段和下游出口段均为直线，直接与U 形渠道连接。三角形量水槽在建造时，把制作好的施工钢模板［20］支撑在U 形渠道的两侧，现浇混凝土即可。三角形量水槽结构如图1 所示，L为槽长、W为槽宽、bc为喉口宽度。

1.2 灌区田间试验系统的布置

灌区田间试验系统由干渠、分水闸门、涵洞、斗渠、矩形渠道、巴歇尔量水槽、U 形渠道、三角形量水槽、节制闸门、水尺等组成（见图2）。因为斗渠低于干渠渠底，所以斗渠通过位于干渠底部的涵洞与干渠连接。涵洞出口连接矩形渠道，巴歇尔量水槽建在矩形渠道中。巴歇尔量水槽按照标准尺寸建造，定期对巴歇尔量水槽进行清淤、水尺零点校准和流量复核等工作，保证测流准确。

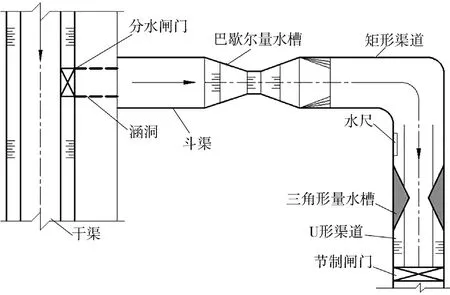
图2 田间试验系统示意

矩形渠道之后与U 形渠道衔接，U 形渠道采用现浇混凝土分段衬砌。每段U 形渠道长5 m 左右，两段之间设有施工缝，三角形量水槽和水位观测井建造在两相邻施工缝之间。三角形量水槽与巴歇尔量水槽距离较短，渠道渗水损失忽略不计。田间试验确保不漏水，避开高温和降雨等不利天气，流量调节范围为0.09～0.23 m3／s。

三角形量水槽分别在槽前、槽后1 m 处设置水位观测井，用来观测上游和下游水深。水位观测井紧靠渠道外侧，观测井内设水尺，水尺精度为0.001 m。水位观测井为圆形，直径为0.45 m。观测井与U 形渠道通过连通管道连接，为充分消除渠道内水流波动对水位的影响，连通管道直径为0.015 m。连通管道与渠道内壁、水位观测井壁垂直连接，并在接口断面处磨平。为避免水位观测井因堵塞、沉降等产生错误读数，在水位观测井位置的渠道内壁上设置倾斜式水尺，倾斜式水尺利用水准仪确定零点后，刻画在U 形渠道内壁上，主要用于复核水位观测井水尺读数。

1.3 量水槽设计参数

量水槽的收缩比ε可用面积收缩比Ac／A0或者宽度收缩比bc／D来表示，其中：Ac为量水槽的喉口断面面积，A0为U 形渠道横断面面积，D为渠道底弧直径。本试验中采用面积收缩比ε＝Ac／A0。量水槽设计时，先初选ε，得到对应的bc，再根据渠道横断面的尺寸得到W，L取W的2～5 倍。为了减少施工钢模板、混凝土等材料用量，降低量水槽的建造成本，将钢模板的展开长度控制在1.189 m 以内。量水槽及U 形渠道参数见表1。

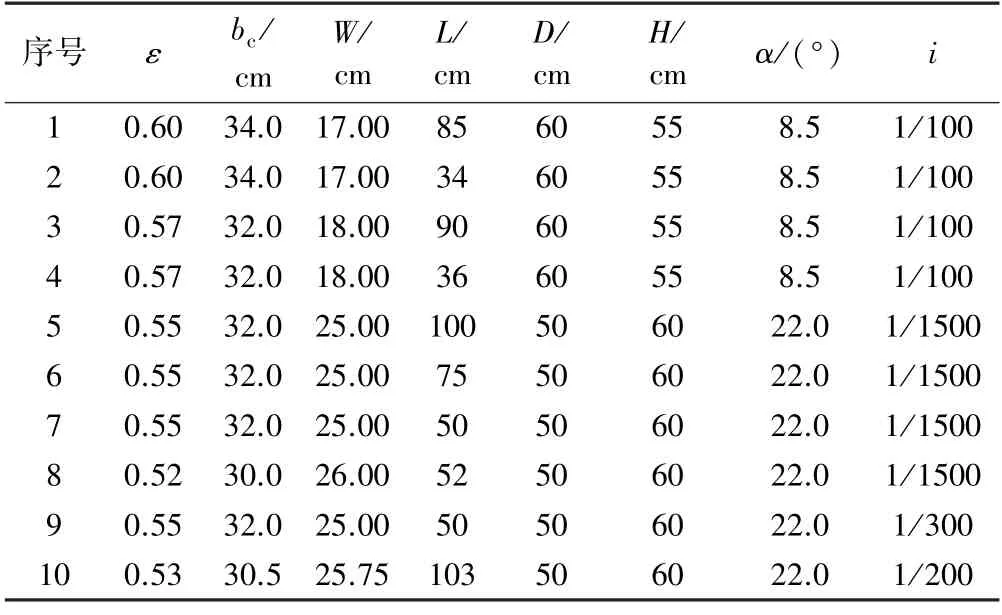
表1 量水槽及U 形渠道参数

2 结果分析

2.1 影响因素

当量水槽槽前为弗劳德数小于0.5 的缓流时，水面平稳、流线水平，有助于获得准确的上游水位，从而保证较高的量水精度。为了探寻影响弗劳德数变化的因素，在不同比降、型号的U 形渠道上，选择不同收缩比、槽长的量水槽进行试验。试验发现槽长对弗劳德数的影响很小，可以忽略不计。为避免数据交叉重叠，以D50 型渠道为例，三角形量水槽弗劳德数与渠道比降、收缩比、流量的关系见图3。由图3 可以看出，在一定条件下，当流量逐渐增大时，三角形量水槽的弗劳德数逐渐减小；当收缩比增大时，弗劳德数增大；当渠道比降增大时，弗劳德数增大。由此可见，流量、收缩比和渠道比降是影响弗劳德数的主要因素。

在渠道内修筑三角形量水槽时，受侧向收缩的作用，上游水深相对无槽时明显升高。目前大多数研究中，通常用量水槽的上游、下游水深之差来表示壅水高度，这种方法并不能准确反映槽前壅水情况。壅水高度定义为有槽和无槽时的上游水深之差。忽略槽长对壅水高度的影响，三角形量水槽壅水高度与流量、收缩比、渠道比降的关系见图4。由图4 可以看出，在其他条件不变的前提下，三角形量水槽的壅水高度随着渠道流量的增大而增大，随着收缩比的减小而增大，随着渠道比降的增大而增大。由此可见，影响壅水高度的主要因素也是流量、收缩比、渠道比降。

2.2 经验公式及限制条件

以弗劳德数为因变量，渠道流量、收缩比和渠道比降为自变量，通过对341 组数据不同的计算模型逐一进行回归分析发现，拟合效果一般，且回归方程量纲不和谐。下面通过量纲分析进一步推求弗劳德数与其影响因素之间的函数关系式。

弗劳德数Fr与流量Q、渠道底弧直径D、渠道比降i、喉口宽度bc、动力黏滞系数μ、重力加速度g等因素有关，可将Fr写成以下的一般函数式：

从式（1）中6 个自变量中选择bc、μ、g作为基本物理量，用4 个无量纲数组成的关系式来表达式（1）。这些无量纲数为

式中：x、y、z、x1、y1、z1、x2、y2、z2、x3、y3、z3为待定指数。

由于Π、Π1、Π2、Π3均为无量纲数，因此式（2）～式（5）的右端量纲应当相同；对于Π和Π3来说，Fr和i是无量纲数，因此：

对于式（3），可写出无量纲式：

用基本量纲［L］、［T］、［F］来表示式（8）中各物理量的量纲，于是：

式（9）两边相同量纲的指数相等，可以得到：

对于式（4），同样按照以上方法可得：

基本物理量所组成的无量纲数均等于1，即：

根据布金汉定理，可用Π、Π1、Π2、Π3、Π4、Π5、Π6组成表征Fr的无量纲数关系式：

式中：Q／（bc2.5g0.5）为相对流量，无量纲数；D／bc为相对直径，宽度收缩比的倒数。

量纲分析的结果表明，Fr是Q／（bc2.5g0.5）、D／bc、i的函数，可以通过试验数据来进一步确定它们之间的定量关系。对341 组试验数据进行回归分析，选用的数学模型为

式中：p为因变量；q1、q2、q3为自变量；a、b、c、d分别为q1、q2、q3、截距的回归系数。

令p＝Fr，q1＝Q／（bc2.5g0.5），q2＝D／bc，q3＝i，将式（15）进行数学变化后进行多重线性回归，回归结果见表2。

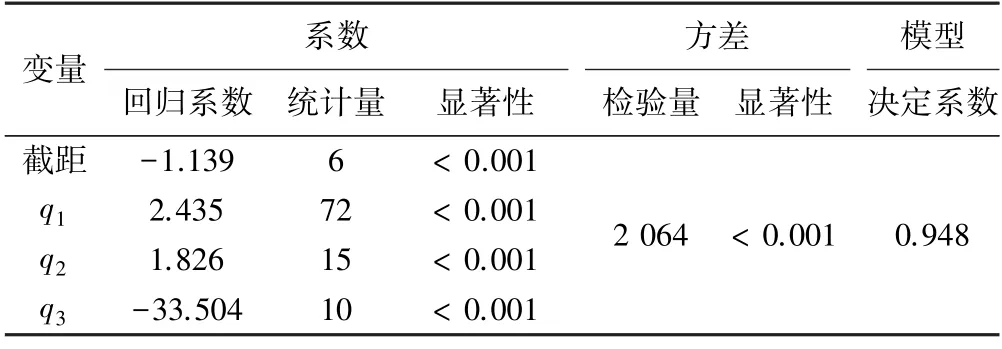
表2 弗劳德数回归结果

从表2 看出，构建的数学模型具有统计学意义，检验量为2 064，显著性小于0.001，决定系数为0.948。Q／（bc2.5g0.5）、D／bc和i对Fr的影响具有统计学意义，显著性均小于0.001。回归系数的正负号与Fr随Q、bc和i的变化情况一致，最终得到Fr的经验公式为

式（16）的适用范围：ε为0.52～0.60、Q为0.09～0.23 m3／s、i为1／1 500～1／100 的D50 型和D60 型U形渠道。将按式（16）计算的Fr与实测Fr进行比较，平均相对误差为2.21%，最大相对误差为7.99%，相对误差小于5%的数据占所有数据的92.1%，相对误差分布情况如图5 所示。

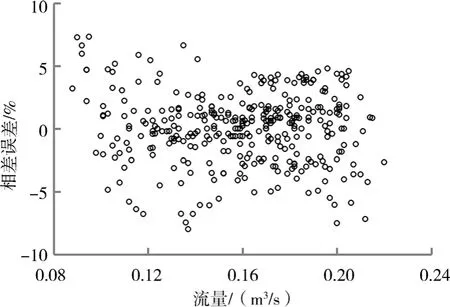
图5 弗劳德数相对误差分布

图6 为弗劳德数相对误差累计频率分布。由图6可以看出，相对误差分布与正态分布函数相吻合，这也表明利用多重线性回归构建的弗劳德数数学模型是可行的。

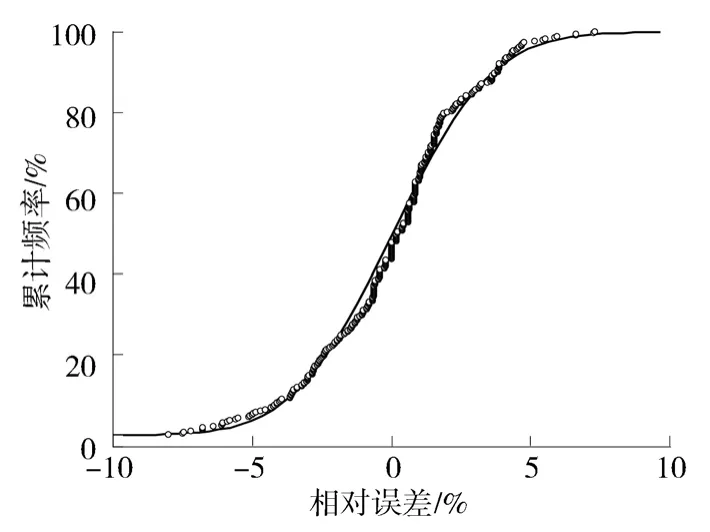
图6 弗劳德数相对误差累计频率分布

对壅水高度hw进行量纲分析，得到相对壅水高度hw／bc是Q／（bc2.5g0.5）、D／bc、i的函数。回归分析后得到hw的经验公式为

将按式（17）计算的hw与实测hw进行比较，平均绝对误差为0.76 cm，95.4%的hw预测值绝对误差小于2 cm（绝对误差分布情况见图7），这里式（17）的适用范围同式（16）。

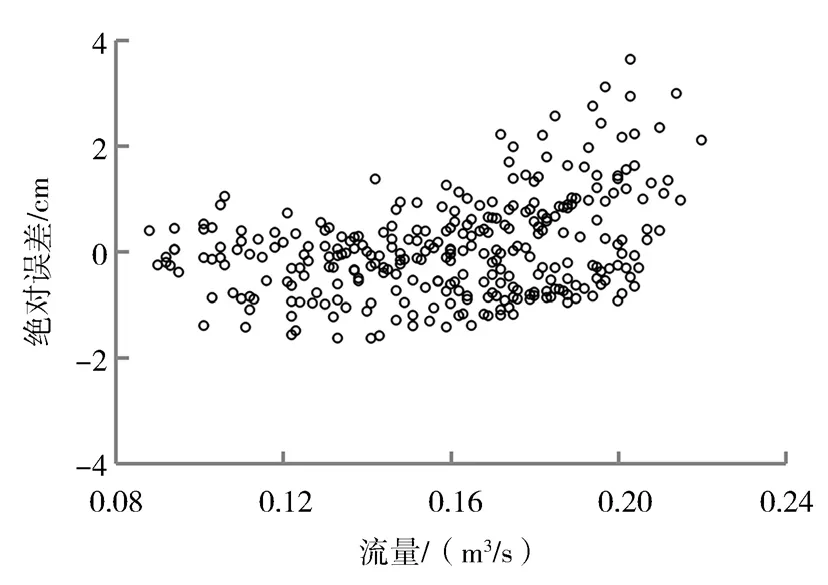
图7 壅水高度绝对误差分布

依据灌溉渠道系统量水规范中关于量水槽的一般规定，上游行近渠内水流Fr不应大于0.5。因此，Fr≤0.5 可以作为确定收缩比的一个限制条件。当收缩比减小时，槽前hw开始变大，逐渐逼近渠道安全超高Fb，直至上游壅水开始漫顶溢出渠道。因此，hw≤Fb可以作为确定收缩比的一个限制条件。

2.3 收缩比范围及适宜收缩比

式（16）、式（17）分别为Fr、hw与Q、D、i、bc之间的定量关系，为确定收缩比提供了基本依据。

基于式（16），令Fr＝0.5，根据Q、D和i等参数计算得到bc。对于三角形量水槽，Fr随着Q的增大而减小，因此只需要验证最小流量Qmin即可，此时bc对应的收缩比即为收缩比的上限。

基于式（17），令hw＝Fb，根据Q、D和i等参数计算得到bc。对于三角形量水槽，hw随着Q的增大而增大，因此只需要验证最大流量Qmax即可，此时bc对应的收缩比即为收缩比的下限。

适宜收缩比取决于按实际需求量水槽所要实现的目标。若以量水槽水头损失小为目标，可利用式（16）的Fr小于且接近0.5 初选收缩比，再按式（17）校核hw是否满足要求；若以量水槽尽可能形成自由出流和保证量水精度为目标，可利用式（17）的hw小于且接近Fb初选收缩比，再按式（16）校核Fr是否满足要求。

适宜收缩比的确定应设计足够多的收缩量，以避免造成量水槽淹没出流；与此同时，收缩量又不能太多，以避免壅水超过渠道安全超高［21］。Fr＝0.5 和hw＝Fb是两个极限情况，以Fr＝0.5 得到最大的收缩比，对应的水头损失最小；以hw＝Fb得到最小收缩比，对应的水头损失最大。因此，可以用中间水头损失方案确定适宜收缩比，即收缩比上、下限的中间值，这种方案考虑了量水槽的淹没保护和安全超高富余，使两者之间达到平衡。

3 讨论

为了验证利用Fr和hw确定收缩比的可靠性，令Fr＝0.5 和Qmin＝0.1 m3／s，选取6 种典型渠道比降，代入式（16）后得到喉口宽度，最终得到渠道不同比降对应的收缩比（见表3）。

表3 基于弗劳德数确定的收缩比

由表3 可以看出，利用Fr确定收缩比时，比降较大的渠道应选择较小的收缩比，比降较小的渠道应选择较大的收缩比，即收缩比与渠道比降是负相关关系。当渠道比降较大时，水流处于Fr ＞1.0 的急流状态，若要槽内形成临界流，并使Fr ＜0.5，必须大幅收缩过水断面，即通过减小收缩比来实现。当渠道比降较小时，水流已经处于Fr ＜1.0 的缓流状态，只要适当收缩过水断面，即可实现Fr ＜0.5。表3 中的收缩比确定结果，验证了文献［1］中关于收缩比与渠道比降关系的观点。

以Fr＝0.5 得到收缩比的上限值。因渠道收缩量最小，故水头损失也最小。但最小收缩量意味着量水槽可能存在淹没出流的风险，导致测流不准确。以Fr＝ 0.5 确定收缩比适用于在已有渠道上修建量水槽，并期望水头损失最小的情况。

将D50 和D60 型U 形渠道的Fb设定为0.2 m，分别令hw＝0.2 m 和Qmax＝0.2 m3／s，选取同样的6 种渠道比降，利用式（17）得到每种渠道比降对应的收缩比（见表4）。

表4 基于壅水高度确定的收缩比

由表4 可以看出，利用hw确定收缩比时，比降较大的渠道应选择较大的收缩比，比降较小的渠道应选择较小的收缩比，即收缩比与渠道比降是正相关关系。主要原因为对于比降大的渠道，因收缩比减小引起的hw变化值较大，所以hw很容易达到安全超高，而比降小的渠道则需要更小的收缩比才能达到。表4 中的结果，与文献［8］中抛物线形喉口式量水槽、文献［10］中直壁式量水槽根据渠道断面参数和渠道比降关系的变化规律一致，也与文献［6］中关于板柱结合型量水槽渠道底坡与收缩比关系的观点一致。

以hw＝Fb得到收缩比的下限值。通过最大限度地减小喉口宽度，量水槽更容易达到自由出流状态［22］，可以获得稳定的水位流量关系。由于渠道收缩量最大，水头损失也最大，槽前壅水过高易导致上游水流溢渠，因此以hw＝Fb确定收缩比适用于对渠道内的流态极其不确定且有足够安全超高的情况。

无论以哪种方法选择收缩比，最终确定的收缩比都必须校核临界淹没度来识别流态，以确保量水槽在自由出流状态下工作。因此，后续应该对临界淹没度进行深入研究。