考虑城市－水库整体风险的汛限水位调整方法研究

史金坤，段志昌，王建有，葛 巍

（1.郑州大学 黄河实验室，河南 郑州 450001；2.中国建筑第五工程局有限公司，湖南 长沙 410004）

0 引言

随着城市化的发展，城市区域进一步扩大，使得越来越多的水库进入了城区，水库的防洪安全对于城市来说越来越重要。另外，对于那些缺水型城市而言，其上游的水库一般要承担向城市供水的重任，城市的参与使得水库的职能发生变动。汛限水位是水库在汛期允许兴利蓄水的上限水位，是防洪调度的起调水位，是协调水库运行管理中防洪与兴利矛盾的关键指标［1］。对于此类水库来说，若仍采用其原设计汛限水位，显然是不合适的，需要对其设计汛限水位进行调整。汛限水位的调整会影响水库的防洪风险和城市供水风险，较高的汛限水位可以减小城市供水风险，但会增加水库的防洪风险。相反，较低的汛限水位能减小水库的防洪风险，但会增加城市供水风险。因此，需要在考虑城市和水库整体风险的基础上来调整汛限水位。

进行风险效益分析可以更科学直观地体现汛限水位调整所带来的利弊效应，为方案的决策提供依据，已有的关于汛限水位调整的研究大都集中在风险效益分析［2］和水位控制［3］两方面，其中水位控制聚焦在分期控制［4］和动态控制［5－6］方面。针对水库职能变化背景下汛限水位的调整也有学者进行了初步尝试［7］。一方面，依据对流域的气候、气象规律的研究，结合降雨预报技术来执行动态变化的汛限水位，但很少考虑水库职能的变化，即使考虑职能变化，也仅仅是对某一特定水库汛限水位调整的必要性进行分析。另一方面，在优选指标的选取上，汛限水位调整所带来的水库供水能力的变化常用供水保证率、可靠度等指标表示［8］，当水库作为备用水源时，缺乏相应的指标表征。鉴于此，本文针对此类水库汛限水位调整方案的决策建立通用的优选指标体系，同时为克服主观权重带来的较大分析负担和客观权重易造成较大误差的不足，采用基于熵权细化主观权重的方法来计算指标权重，建立考虑城市－水库整体风险的汛限水位调整方案模糊优选模型，以期为水库汛限水位的优化调整提供一种新思路。

1 考虑城市－水库整体风险的汛限水位调整方案优选模型构建

1.1 优选指标的确定

汛限水位调整方案决策涉及的指标较多，很多指标之间有互相竞争甚至互相矛盾的关系，本文根据研究对象的特性将指标分为两部分，即水库自身风险指标和下游城市风险指标。水库自身风险主要为水库自身的防洪风险，下游城市风险包括下游城市防洪风险和城市供水风险，在防洪风险指标方面，参考已有研究成果，选取较为常用的防洪风险率和易损度指标；在供水风险指标方面，引入适用性更广的供水风险率指标，由此建立汛限水位调整方案优选指标体系，见图1。

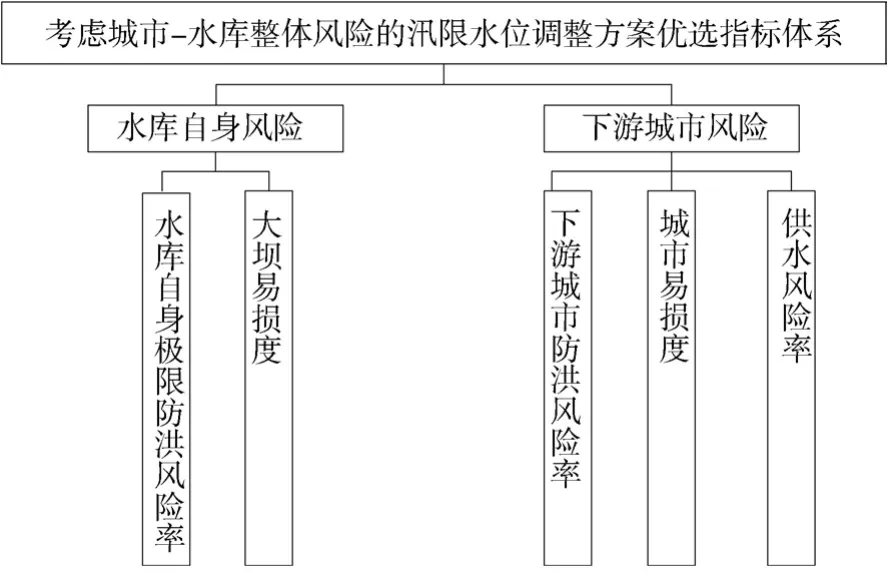
图1 汛限水位调整方案优选指标体系

水库自身极限防洪风险率（R自）常用于水库自身防洪风险的定量分析［9］，即库水位超过水库校核洪水位（Z校）的概率。通过对各起调水位调洪演算结合频率分析法就可求出不同汛限水位下的水库自身极限防洪风险率R自。

式中：Zm为洪水调节最高水位，P为频率。

下游城市防洪风险率（R下）常用于下游城市防洪风险的定量分析，即水库下泄流量超过下游河道安全流量的概率。一般情况下，当库水位超过防洪高水位时水库下泄流量将超过下游河道安全流量［10］，这样下游城市的防洪风险率就可以用库水位超过防洪高水位的概率来表示。

式中：Q为水库下泄流量，Q安为下游河道安全流量；Z为库水位，Z防为防洪高水位。

易损度表示大坝和下游防护对象遭遇险情的严重程度，对于大坝，当总库容一定时，库水位越高，溃坝造成的后果越严重；对于下游防护对象，水库泄流量越大，可能造成的淹没损失越大［11］。在此采用调洪最高水位超过Z校的幅度表示大坝易损度（R坝），调洪最高水位超过Z防的幅度表示城市易损度（R城），其中大坝易损度的最大值为坝顶高程与校核洪水位的高差，若调洪最高水位高于坝顶高程，其大坝易损度为此最大值。

抬升汛限水位会增加汛期水库的蓄水量，减少汛期弃水，使得水库在汛期结束后更容易蓄较多的水。因此，可以认为水库在一整年内的存水越多，城市供水风险就越小；相反，存水越少，城市供水风险就越大。不同水库供水形式有所不同（如持续供水、应急供水等），其供水风险的表征就会不同，在此引入一种通用的供水风险表示方法，即假定水库一整年内能蓄到满足城市用水的水量时，此汛限水位下城市就无供水风险。具体为：首先根据来水与用水情况计算水库的最大蓄水量（Wm），见式（3），然后可用供水风险率（R水）来表示不同汛限水位下的城市供水风险，此指标也可以通过转换来反映不同汛限水位的缺水量，计算公式见式（4）。

式中：W来为水库来水量（如非汛期上游来水、调水工程引入水等），W用为除供水用途（城市生活用水、紧急备用水等）外的用水量（如生态用水、蒸发渗漏损失水等）。

式中：W满为满足城市用水需求的水库库容，ΔW为W满与原设计汛限水位对应库容的库容差。

1.2 基于熵权细化主观权重的优选指标权重确定

本文采用基于熵权法细化主观权重的方法来确定指标权重，首先根据专家的意见确定防洪和城市供水两个目标的相对重要程度，得出两者经验权重，然后在每个目标下通过熵权法［12］分别计算属于该目标的下一级指标权重，进而得出所有指标的权重值。该方法既充分体现了决策者的主观偏好，又不增加决策分析者的负担，同时体现出熵权法依据客观数据赋权的客观性优势，该方法可以更科学地对指标进行赋权。

1.3 基于模糊优选模型的方案优选

模糊优选模型是在模糊数学模糊集理论的基础上发展而来的，其可以充分考虑系统模糊性、不确定性及复杂性［13］，通过隶属函数把目标体系和最优决策方案联系起来，利用模糊优选公式计算相对隶属度，根据定量化的相对隶属度值来评价方案的优劣。由于不同的汛限水位方案对防洪和城市供水的侧重有所不同，最优方案的确定是一个多目标多层次的复杂决策问题，在决策过程中往往存在重要影响因素无法量化的问题，因此模糊优选模型对其有较好的适用性。具体步骤如下。

1）建立优选指标相对隶属度矩阵。设待优选的汛限水位共有n个方案，每个方案有m个指标值，则有方案集的指标特征值矩阵X：

式中：xij为方案j的第i个指标值（i＝1，2，…，m；j＝1，2，…，n）。

各指标的量纲不同，需对指标进行归一化处理［14］（本文建立的指标均属越小越优型），得到相对隶属度矩阵R＝（rij）。

式中：rij为方案j指标i的隶属度，maxxi、minxi分别为方案集中指标i的最大、最小值。

2）计算优选指标的权重。根据1.2 节可以得到各指标的权重值，从而得出指标权重向量W＝（wi）。

3）计算各方案的优属度μj：

式中：p为距离参数，p＝1 为海明距离，p＝2 为欧氏距离，本文取p＝2，即采用欧氏距离进行计算。

计算结果表示各方案对于优等方案的隶属度，即各方案的优属度，优属度最大的方案即为最佳方案。

2 实例应用

2.1 水库概况

尖岗水库位于淮河水系颍河支流贾鲁河干流上游的尖岗村西，距郑州市区6 km，水库控制流域面积113 km2。由于该水库居于郑州市区上游，下游有多条铁路、公路，还有水厂、电厂等供水及能源设施，还是人口、经济的高度聚集区，防洪位置十分重要，因此按大型水库进行管理。水库现状正常蓄水位为154.75 m，总库容6 070.41 万m3；设计洪水标准为100 a 一遇，校核洪水标准为5 000 a 一遇＋15%安全保证值（折合洪水频率为0.008%）；汛限水位150.55 m，设计洪水位153.01 m，校核洪水位156.96 m。根据河南省防办编制的《河南省大型及重点中型水库汛期调度运用计划》，水库主汛期为6 月21 日—8 月15 日，库水位低于溢洪道底部高程时采用泄洪洞泄洪，库水位高于溢洪道底部高程时由溢洪道自由泄洪。

尖岗水库续建时规划该水库功能是以防洪、城市供水、农田灌溉为主，兼顾发电、养鱼等综合利用，由于上游来水不足，失去了发电和灌溉等功能，随着黄河水的引入、南水北调中线工程的通水以及郑州市社会经济的快速发展，水库的主要职能变为防洪和城市紧急供水，而汛限水位多年未变，水库在汛期结束后往往无水可蓄，不利于城市紧急供水。

2.2 尖岗水库汛限水位调整方案模糊优选模型

2.2.1 防洪风险率与易损度指标

考虑到尖岗水库原有特征水位和实际情况，本文拟定150.55、150.75、150.95、151.15、151.35、151.55 m等6 个汛限水位方案。根据尖岗水库历年实测洪水资料，将典型洪水按洪峰、洪量同频率进行放大，推求不同频率的设计洪水过程，此处频率P的取值分别为0.008%（校核洪水）、0.01%、0.02%、1%、2%。然后以各方案为起调水位，按规划调度方式调节各频率的洪水，可得各方案调洪高水位，见表1。

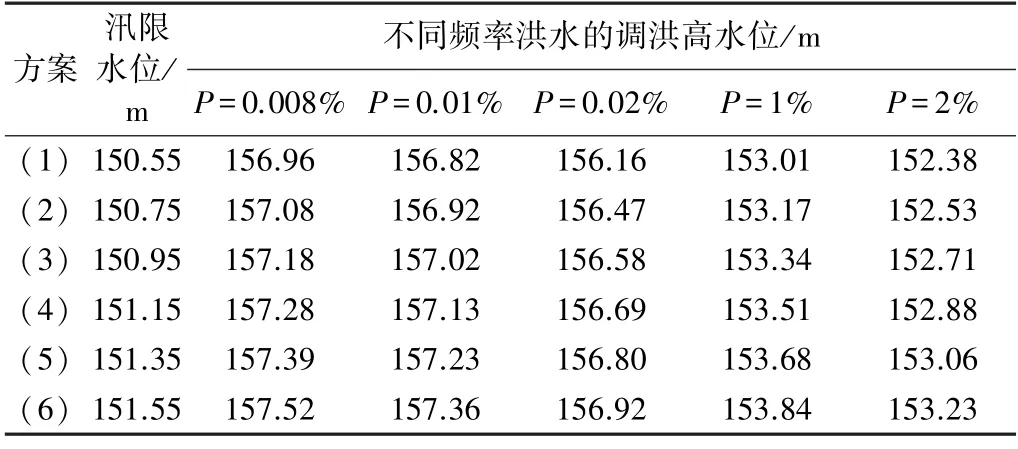
表1 不同汛限水位下各频率洪水的调洪高水位

尖岗水库下游贾鲁河经过综合治理后最大防洪标准达到100 a 一遇［15］，因此防洪高水位与设计洪水位相同。根据2.1 中的方法可计算出水库自身极限防洪风险率（R自）、下游城市防洪风险率（R下）、大坝易损度（R坝）和城市易损度（R城），结果见表2。从表2 中可以看出，随着汛限水位的抬升，防洪风险率和大坝、城市易损度都逐渐增大。

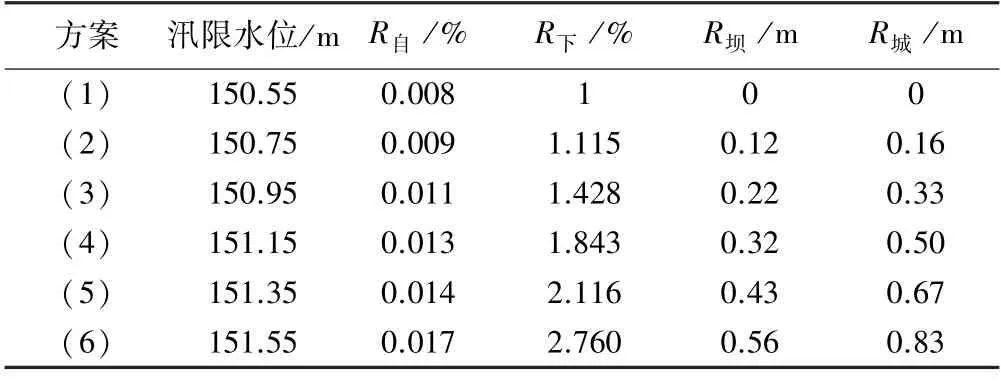
表2 不同汛限水位下的防洪风险率和易损度

2.2.2 供水风险率指标

尖岗水库正常蓄水位对应的蓄水量可满足城市紧急用水需求，因此W满为正常蓄水位对应的库容。汛期水位一般都维持在汛限水位，因此尖岗水库最大蓄水量计算中来水主要考虑非汛期的上游来水，此处月增蓄水量的计算中去除6—8 月的数据（见表3）。不同水平年上游来水量不同，可选取年径流量与多年平均值接近的平水年进行计算，根据尖岗水库设计平水年的月均流量值（见表3），扣除蒸发、渗漏损失和生态用水，损失系数取0.9［16］，可得出水库的最大蓄水量，由式（4）可得各汛限水位方案的城市供水风险率（R水），结果见表4。从表4 中可以看出，随着汛限水位的抬升，水库非汛期可蓄到的最大水量逐渐增大，R水逐渐减小。

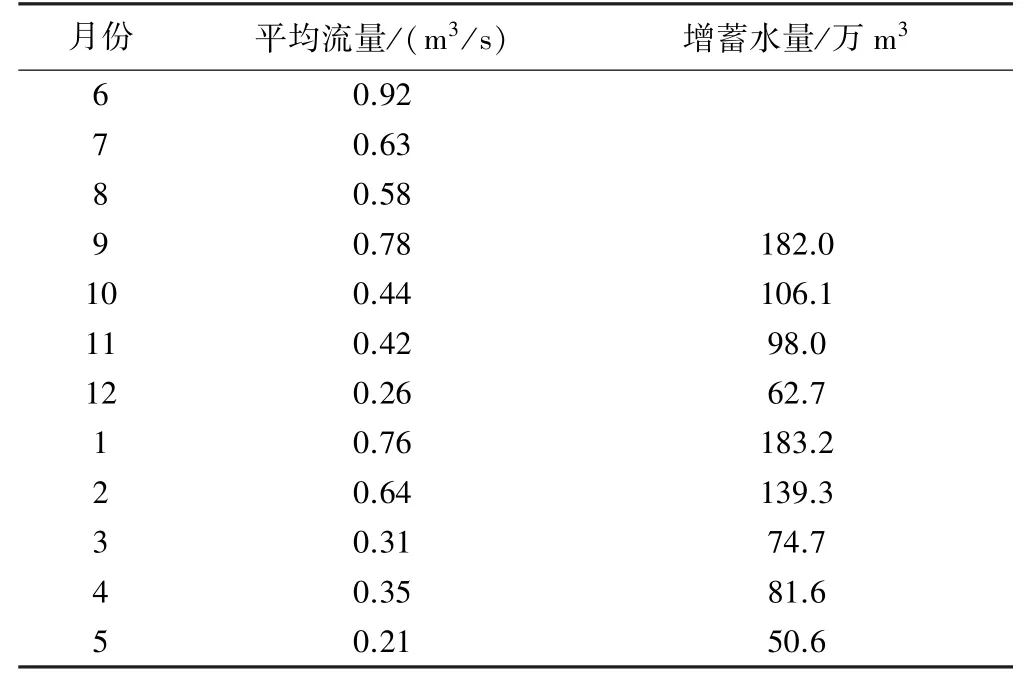
表3 尖岗水库设计平水年的月均流量及增蓄水量

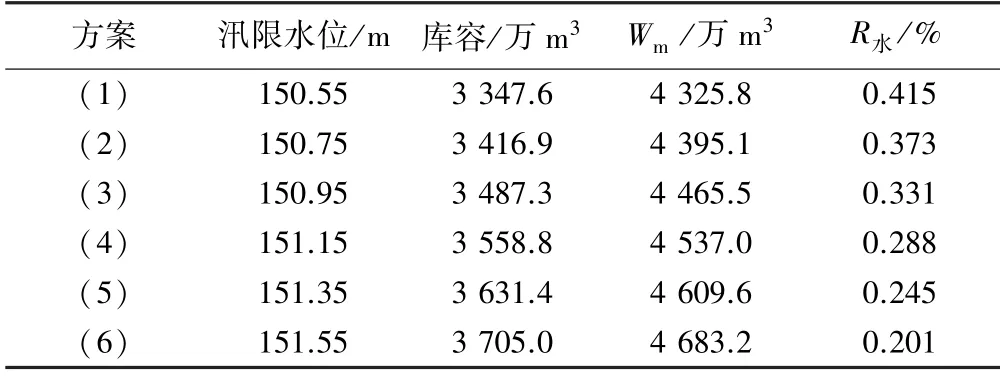
表4 不同汛限水位下的城市供水风险率

从风险率的角度看，随着汛限水位的抬升，防洪风险逐渐增大，城市供水风险逐渐减小（见图2），此处也明显体现出汛限水位调整中水库防洪任务与供水任务的竞争性。

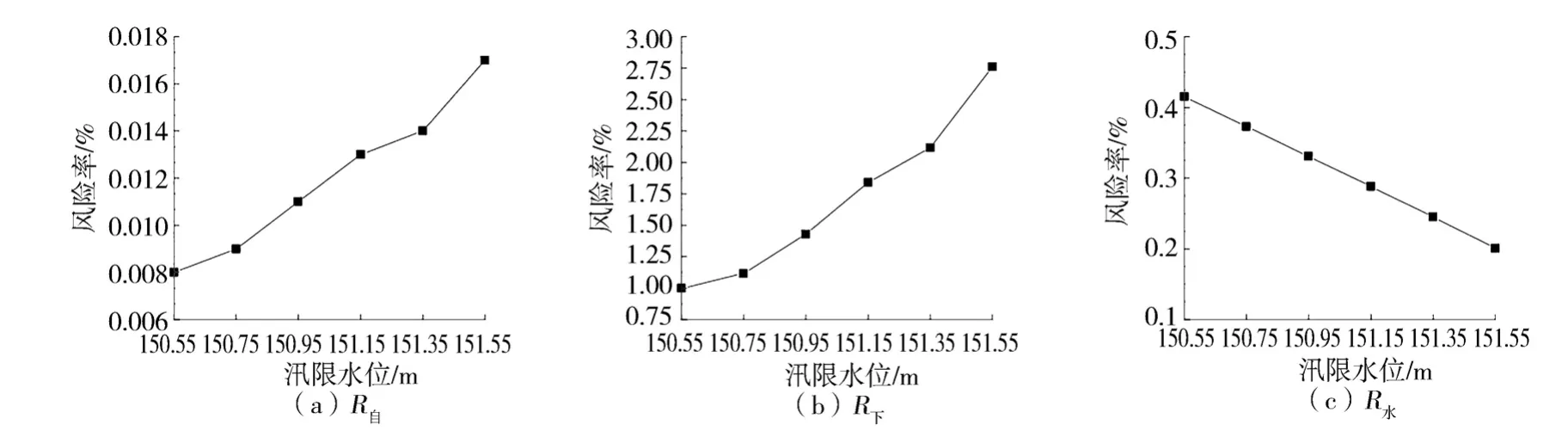
图2 不同汛限水位下风险率的变化

2.2.3 最优汛限水位方案的确定

根据图1 中的指标体系和表1 调洪演算结果可求出各指标值（见表5），则可以建立优选方案的特征值矩阵X，根据式（6）可得特征值的相对隶属度矩阵R。

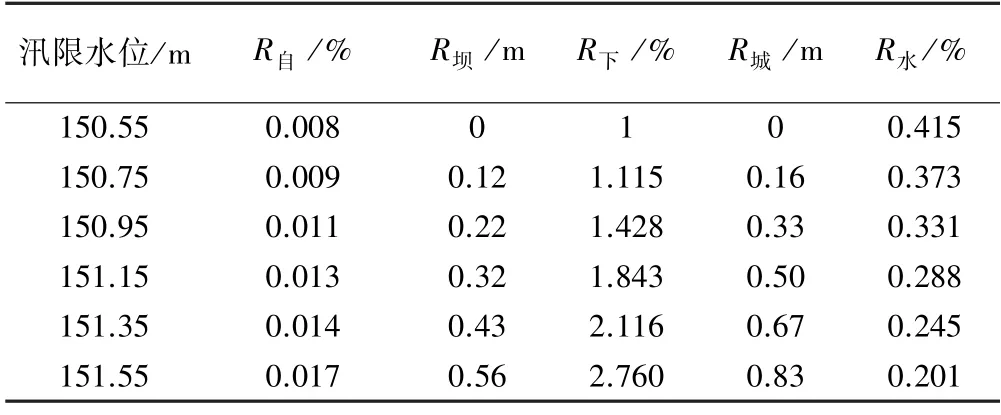
表5 尖岗水库汛限水位调整方案优选指标体系

汛限水位调整方案优选指标可以分为两类，一类是防洪目标（R自、R下、R坝和R城），另一类是供水目标（R水）。当决策者目标重要度偏向防洪目标时，如两者权重之比为0.6 ∶0.4，在防洪目标下属指标中根据熵权法计算熵权，进而得出最终参与优选的指标权重，结果见表6，因此权重向量W＝（0.141 7，0.156 5，0.133 5，0.168 3，0.400 0），模型参数建立完备。

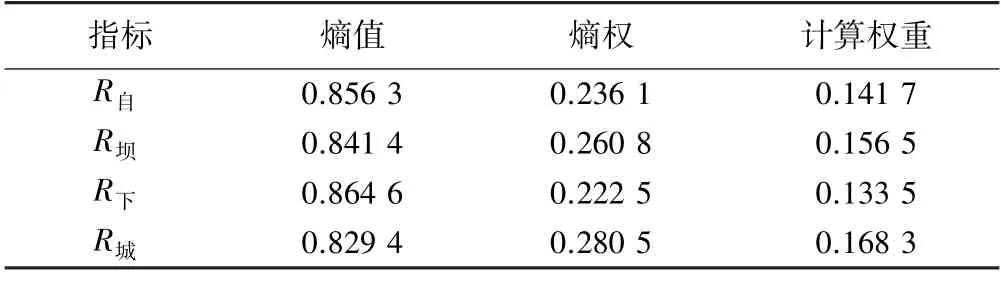
表6 熵权法细化主观权重计算结果

根据式（7）可计算出各方案的优属度，结果为μ＝（0.361 8，0.402 0，0.472 0，0.574 1，0.659 5，0.638 2），方案（5）为最优方案，即最优汛限水位为151.35 m。

同理，当决策者目标重要度偏向供水目标时，如两者权重之比为0.4 ∶0.6，此时权重向量W＝（0.094 4，0.104 3，0.089 0，0.112 2，0.600 0），μ＝（0.100 7，0.154 6，0.344 6，0.651 1，0.861 6，0.899 3），方案（6）为最优方案，即最优汛限水位为151.55 m。

指标特征值和方案优属度计算结果表明，在水库职能变化后综合考虑防洪和供水目标的情况下，相较于原设计汛限水位，在偏好防洪目标或供水目标时，汛限水位分别提高了0.8 m 和1.0 m，分别为151.35 m 和151.55 m，水库自身极限防洪风险率由0.008%增大到0.014%和0.017%，下游城市防洪风险率由1%增大到2.116%和2.760%，供水风险率由0.415 减小到0.245和0.201。在汛期的不同阶段，往往会有不同的目标偏好，决策者越偏好防洪目标最优汛限水位越低，越偏好供水目标最优汛限水位越高，该模型可在决策者不同偏好的基础上进行最优方案的决策。当防洪与供水目标的权重较为合理时，通过模糊优选模型所确定的最优方案最接近理想最优方案，为最符合工程实际状况的方案，因此建议在确定防洪与供水目标相对重要度时，应咨询领域内相关专家，以确定合理的指标权重，从而确定更加合理的汛限水位调整方案。

3 结束语

本文综合考虑城市－水库整体风险，提出了城市化发展造成水库职能变化背景下水库汛限水位调整的方法，针对水库供水形式的不同，引入通用的城市供水风险表示方法，并应用数学计算方法进行最优汛限水位方案的决策，为该类水库汛限水位的优化调整提供了新的思路。本文只对水库矛盾突出的防洪风险和城市供水风险进行了研究，下一步可以融合发电、航运、灌溉等多个调度目标建立内容和适用性更加广泛的汛限水位控制模型。