无黏性土颗粒起动临界水力梯度的计算模型

2023-11-10赵耀威高笑娟

人民黄河 2023年11期

赵耀威，李达，高笑娟，焦雷

（1.河南科技大学土木工程学院，河南洛阳 471023；2.中铁十五局集团城市轨道交通工程有限公司，河南洛阳 471002）

0 引言

渗流作用下，无黏性土颗粒的起动流失作为渗透变形的直观表现形式，会对砂砾石地基和堤防结构等工程造成严重的不良影响［1－3］。相关研究多集中于影响渗透变形发生的土体本身几何条件和外部水力条件两方面［4］。几何条件包括颗粒级配、密实度、孔隙率等，决定土体内部结构的稳定性，并且由土体颗粒级配和相对密度来决定内部结构稳定的方法已经相当成熟［5－7］；水力条件包括水力梯度的大小和方向，是驱动土体颗粒起动流失、导致渗透变形的外部条件，一般采用临界水力梯度来描述。

对于土体渗透变形的水力条件，研究手段以土体颗粒移动流失的力学分析法为主，根据颗粒在渗流作用下的受力平衡来计算渗透变形发生的临界水力梯度。太沙基公式便是利用土体颗粒所受的渗透力与其水下浮重相平衡的原理，获得均匀土渗透变形发生的水力条件［8］，其形式为

式中：icr为渗透变形发生的临界水力梯度；Gs为土体相对密度，Gs＝γs／γw，其中γs为土颗粒重度、γw为水的重度；n为土体孔隙率。

不同于均匀土渗流作用下局部土体或颗粒群移动流失的表现形式，不均匀土渗透变形的表现形式主要为管涌，即渗流作用下较细颗粒通过较粗颗粒所形成的基质间隙不断地迁移流失［9］。根据此特点，康德拉且夫认为渗流作用下土体颗粒上作用有3 个力，即颗粒在水中的自重、渗流对土体颗粒产生的拖曳力、渗流产生水头差分布在单个颗粒上的作用力，并根据力的平衡关系给出了确定临界水力梯度的关系式［10］：

式中：d0为无黏性土的等效管道孔径，d为可动颗粒粒径。

Indraratna 等［11］基于等效孔径的概念，提出了一种土体中细颗粒沿孔隙通道迁移流失的理论模型；许波琴等［12］在该模型基础上对颗粒进行力和力矩的平衡分析，探讨了颗粒起动方式的影响；王霜等［13］考虑周围颗粒对水流拖曳力的影响，重新进行颗粒受力的平衡分析，获得了散粒土管涌发生的临界水力梯度表达式；Huang 等［14］根据绕固定颗粒滚动的极限力矩平衡条件，得到了考虑相对固定颗粒不同暴露位置的临界水力梯度计算公式；王明年等［15］在考虑土体有效应力和细颗粒应力折减的情况下，建立细颗粒的受力模型，获得临界水力梯度计算公式。

调研发现，众多学者虽然对颗粒起动临界水力梯度进行了大量的研究，但是存在忽略特定边界条件、考虑影响因素单一的问题，鲜有在考虑孔隙管道几何边界条件下综合多种影响因素来计算临界水力梯度的研究成果，同时，多种因素对临界水力梯度的影响规律也有待进一步探讨。

在已有研究的基础上，本研究提出了一种考虑多种因素影响的松散颗粒沿孔隙管道起动流失的理论模型。基于变截面孔隙管道的几何边界条件，结合刘忠玉等［7］对无黏性土颗粒的分类，对孔隙管道中一般存在状态的可动颗粒和临界存在状态的阻塞颗粒分别进行了起动流失的运动力学分析，引入相对遮挡度、相对暴露度和应力状态等的关键影响因素，根据力矩平衡方程获得颗粒起动流失临界水力梯度的计算模型，并利用已有的试验资料验证了该模型预测临界水力梯度的有效性和优越性。此外，还分析了渗流方向、相对遮挡度以及相对暴露度等参数对临界水力梯度的影响规律。

1 颗粒移动流失的几何边界条件

无黏性管涌型土由骨架颗粒和松散颗粒两类土颗粒构成［7］。根据其渗透变形的表现形式，用一组不相连的流体导管模拟骨架颗粒堆积形成孔隙系统的几何形状，形成变截面的孔隙管道模型，如图1 所示［5］。作为松散颗粒移动流失的几何边界条件，这些由骨架颗粒构成的管道平行于流动方向，管道最小孔径d0和最大孔径dmax由以下公式确定［7］：

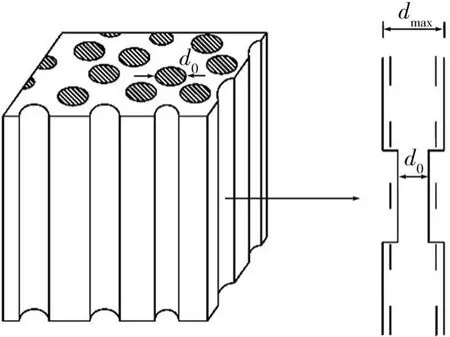
图1 变截面的孔隙管道模型

其中

式中：λ为土体颗粒的形状系数，对于球形颗粒λ取6；na为仅由骨架颗粒组成假想土体的孔隙率；e为天然土体的孔隙率；ya为天然土体中松散颗粒的含量，以小数表示；Dh为骨架颗粒的有效粒径；ΔSi为骨架颗粒中第i粒组的质量含量；Di为第i粒组的代表粒径。

基于骨架颗粒形成的变截面孔隙管道模型，假设孔隙管道的孔径为d0，根据Poiseuille 定律，单个孔隙管道的水流流量Q0为

式中：i为管道水力梯度，μw为水的黏滞度。

那么，孔隙管道中的水流流速v为

式中：S为单个孔隙管道的横截面面积。

2 颗粒起动的理论模型

鉴于变截面孔隙管道对发生移动颗粒粒径的限制关系，选取直径d0的孔隙管道单元作为颗粒移动流失的几何边界条件，其中心位于流线上，θ表示其相对于竖直轴的方位角。结合无黏性土颗粒的分类，对孔隙管道中可动颗粒的一般存在状态和阻塞颗粒的临界存在状态分别进行颗粒起动流失的运动力学分析，同时，假设孔隙管道单元中水流为稳态流动。

2.1 d＜d0 的可动颗粒一般存在状态

一般存在状态下可动颗粒的粒径大小决定了颗粒并不会以单一粒子的形式存在于孔隙管道单元中，即颗粒起动的运动力学分析需考虑周围颗粒的影响，为此，引入周围颗粒的相对遮挡度和相对暴露度两个参数进行颗粒受力分析。

渗流作用下，可移动颗粒A的受力如图2 所示，受到的力包括水流拖曳力FD、水下浮重G′、静水压力FP、周围颗粒的支持力N以及颗粒之间的摩擦力Ff。其中：水流拖曳力可利用颗粒在黏滞层流中所克服的阻力计算，其大小与孔隙流速有关，孔隙流速越大，颗粒所受到的拖曳力也越大，作为水流流过粗糙颗粒表面而产生的摩擦力，其方向因受到周围颗粒的影响不一定沿颗粒的运动方向，而是结合相对周围颗粒的位置关系，考虑利用相对上游颗粒的遮挡度以及下游颗粒的暴露度来判断拖曳力的作用方向，即拖曳力方向沿周围颗粒所形成的理论床面；静水压力FP为作用在颗粒投影面积上的水压力差，结合达西定律可知，其方向与孔隙管道中的水流方向一致。颗粒A运动时，沿周围颗粒B表面发生滚动，这时的摩擦力即为两颗粒之间的滚动摩擦力，因其产生的力矩为零，计算时将其忽略。

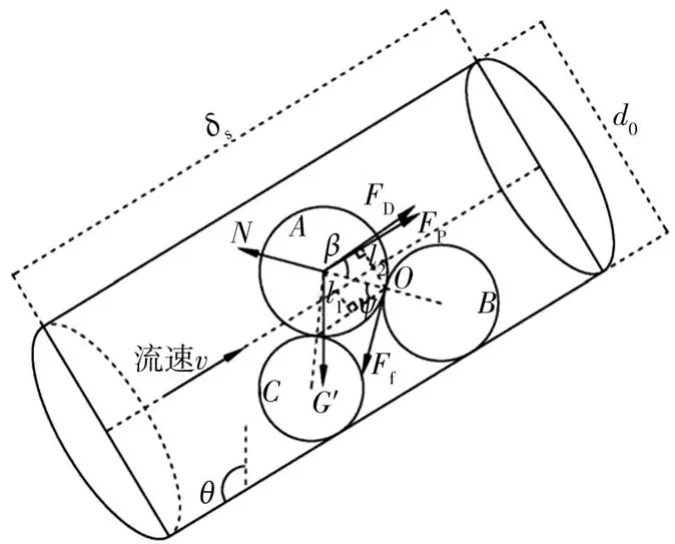
图2 一般存在状态颗粒起动的受力示意

随着水力梯度的增大，水流对颗粒的驱动作用逐渐增大，最终达到使颗粒A所受各力绕其与下游颗粒接触点O的合力矩为零时，颗粒A达到极限平衡状态，此时孔隙管道中的水力梯度即为一般存在状态颗粒起动流失的临界水力梯度。

以颗粒A、B之间的接触点O为中心建立力矩平衡方程：

式中：d为可移动颗粒A的直径；θ为孔隙管道方向与竖直方向的夹角；β为可移动颗粒的暴露角，即渗流方向与颗粒A、B中心点连线的夹角，其正弦值象征相对下游颗粒的暴露度，可由l2表示，sinβ＝l2／r，r为可动颗粒A的半径；ψ为遮挡角，即周围颗粒接触点连线和其中心点连线的夹角，其正弦值象征周围颗粒的遮挡度，可由l1表示，sinψ＝l1／r。

静水压力FP由达西定律经数学简化推导得到［11］：

式中：δs为孔隙管道单元的长度，可取δs＝d。

拖曳力FD（阻力）根据Stokes 定律计算得到［16］：

水下浮重G′计算公式为

把以上各力的计算公式代入力矩平衡方程可得一般存在状态下颗粒起动临界水力梯度i的计算公式：

2.2 d ＝d0 的颗粒临界存在状态

阻塞颗粒作为松散颗粒存在于孔隙管道中的临界状态，颗粒起动流失时需考虑其应力状态的影响。同时，引入Skempton 的应力折减系数α来表示细颗粒因无法完美填充骨架颗粒孔隙而承受较低应力的折减程度。

假设土体为连续、均匀、各向同性材料，可以看作半无限空间的弹性体，那么自重作用下任意土体单元的应力状态均可简化为侧限应力状态，如图3（a）所示。为了便于分析，沿渗流方向建立mon坐标系，则渗流作用下该土体单元斜截面的应力状态如图3（b）所示。

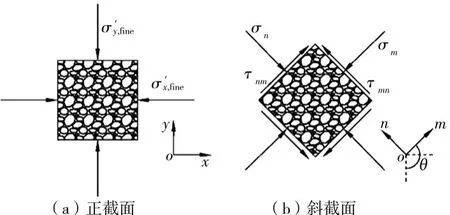
图3 土体单元的应力状态［15］

用应力矩阵的形式可以表示为

式中：σm为m方向（平行于渗流方向）的正应力；σn为n方向（垂直于渗流方向）的正应力；τmn为n方向的切应力；τnm为m方向的切应力为渗流作用下土体单元所受到的水平方向有效应力为渗流作用下土体单元所受到的竖向有效应力。

渗流作用下，阻塞颗粒的受力如图4 所示，受到的力包括孔隙管道的压力FN、阻塞颗粒与孔隙管道的摩擦力Ff、水下浮重G′和作用于颗粒表面的静水压力FP。对于孔隙管道的压力FN，可将上述斜截面的应力状态应用于孔隙单元中的阻塞颗粒上求得，同时，考虑阻塞颗粒接触的实际情况需对其所受应力作出调整。因此，阻塞颗粒不承受m面上的应力，n面上的切向应力因颗粒运动状态的改变而发生变化，并随着孔隙管道作用于颗粒上正应力的增大而增大。此外，因阻塞颗粒表面无水流流过，故颗粒不承受水流拖曳力的作用［11］。

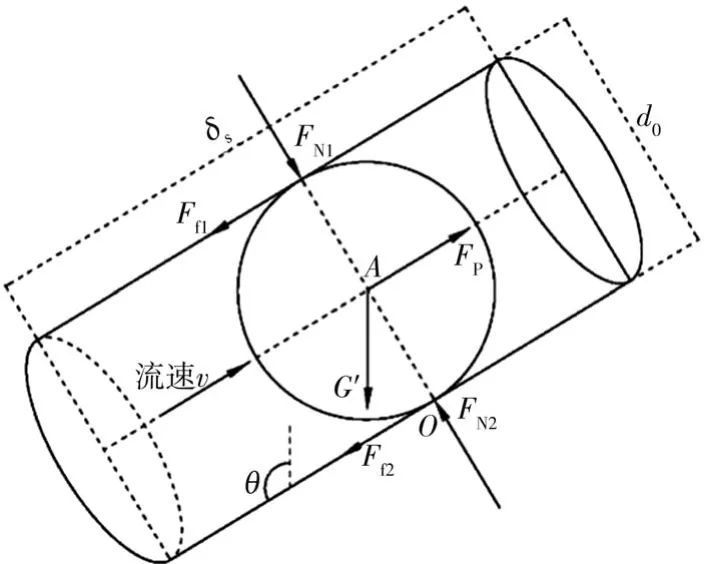
图4 阻塞颗粒受力示意

以阻塞颗粒与孔隙管道的接触点O为中心建立力矩平衡方程：

阻塞颗粒与孔隙管道的摩擦力Ff按照下式计算：

其中

式中：f为摩擦系数，无黏性土f＝tanφ′，φ′为土体的有效内摩擦角；s为σn的作用面积，取πd2／4。

其余力的计算方式同前，各计算公式代入力矩平衡方程可得临界存在状态下颗粒起动临界水力梯度i的计算公式：

式中：K0为土体的静止土压力系数，无黏性土K0＝1－sinφ′。

经过对孔隙管道中两种存在状态颗粒的运动力学分析，临界存在状态仅有静水压力驱动以及受到应力状态的影响，颗粒起动流失所需要的水力梯度更大，因此出于安全考虑，将一般存在状态颗粒起动的临界水力梯度作为无黏性土发生渗透变形的临界水力梯度。

3 模型验证

为验证理论模型对颗粒起动临界水力梯度预测的准确性，利用有关文献中所列部分土样数据进行校验。数据来源其一是Skempton 等［17］根据自行配制的4 种砂砾料所进行的室内管涌试验研究，其中试验土样C、D 是内部稳定的；其二是Ahlinhan 等［18］利用专门研制的试验装置，对5 种不同无黏性土进行的垂直和水平渗流试验研究，试验中改变了土样的初始相对密度且土样A1、A2 为内部稳定土，故选取土样A、B、E1、E2、E3 分别进行校验。需要说明的是不同试验认定管涌发生的临界条件存在差异，理论模型中无法选择统一的颗粒粒径作为管涌发生的认定颗粒，因此根据已有研究的分析成果，同时出于安全考虑，对于Skempton管涌试验，假定土颗粒流失量达到土体质量的5%时，所对应的水力梯度为土体颗粒移动流失的临界水力梯度，即颗粒粒径取d＝d5（d5为小于该粒径的土颗粒占土体总质量的5%的粒径），同样地，对Ahlinhan 管涌试验选取d＝d10（d10为小于该粒径的土颗粒占土体总质量的10%的粒径）。具体校验过程如下。

首先，根据天然土体的级配曲线计算界限粒径xa［7］，划分骨架颗粒与松散颗粒，然后计算仅由骨架颗粒组成假想土体的有效粒径Dh，并将该假想土体的孔隙率na和计算所得Dh代入式（3），获得由骨架颗粒形成孔隙管道的最小直径d0。各试验土样计算结果见表1。

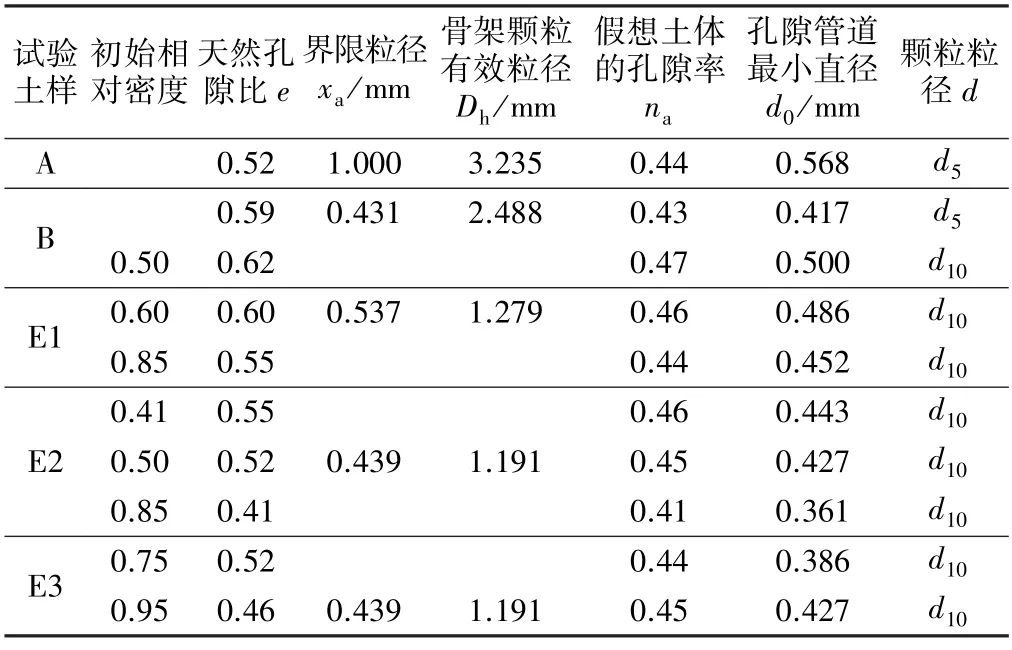
表1 试验土样参数及计算结果

其次，引用斜坡上泥沙颗粒相对暴露度的均值计算公式［19］，计算水平渗流条件下颗粒的相对暴露度，取sinβ＝0.785，垂直渗流条件下相对暴露度取值为0.798；对比暴露度与遮挡度，其二者均表示可移动颗粒A 相对周围颗粒的位置关系［20］，因此考虑遮挡度同暴露度一样，也假定其分布规律服从偏正态分布，同样可采用斜坡上颗粒相对暴露度的均值公式计算，其具体取值与暴露度相同。

最后，利用模型实现对试验土样临界水力梯度的预测，并将预测数据与试验数据的分布散点绘于图5中。散点分布越靠近图中45°线，表示数据吻合程度越高，模型预测颗粒移动临界水力梯度的效果越好。由图5（a）可以看出，水平渗流条件下，散点位置大致位于45°线两侧，试验值与预测值之比的均值与1 的偏差为0.109 6，振荡系数为0.128，两组数据具有较高的吻合程度；垂直渗流条件下，两组数据也同样具有较好的一致性，如图5（b）所示，试验值与预测值之比的均值与1 的偏差为－0.003 4，振荡系数为0.154。经过与文献方法计算结果［4］比较可知，无论是水平渗流还是垂直渗流，理论分析模型对颗粒起动流失临界水力梯度的预测都具有较高的准确性，模型的有效性得以验证。

此外，因理论分析模型对临界水力梯度的预测公式与康德拉且夫法计算公式具有相同的形式，将其预测的数据点绘于图5（b）中，可知采用康德拉且夫法预测颗粒移动临界水力梯度的部分数据点远离对角线区域，数据误差较大，试验值与预测值之比的均值与1 的偏差达到0.260。可见本文提出的计算模型预测颗粒起动临界水力梯度的准确性显著优于康德拉且夫法的预测结果。

4 临界水力梯度的影响分析

4.1 渗流方向

渗流方向角θ与临界水力梯度预测值icr的关系如图6 所示。可以看出，在相同渗流方向下，颗粒起动的临界水力梯度随着颗粒粒径的增大而增大，这与模型试验的结果一致［21］；而对于相同粒径的颗粒，虽然垂直渗流临界水力梯度大于水平渗流临界水力梯度这一预测结果与Ahlinhan 等［18］的渗流试验结果相同，但是其变化趋势受相对下游颗粒暴露位置的影响，随着渗流方向角的增大，临界水力梯度呈现先增大后减小的趋势。

从颗粒受力分析的角度可以做出很好的解释：在相对暴露度的影响下，不同渗流方向上土颗粒自重对颗粒临界驱动力的贡献程度不同。位于孔隙管道单元中的可动颗粒绕其与下游颗粒接触点滚动时，若渗流方向角小于颗粒的暴露角，则颗粒自重将同样作为颗粒起动的驱动力，颗粒本身依靠自重便能实现在孔隙管道中的起动流失，随着渗流方向角的增大，颗粒自重的驱动作用越来越小；若渗流方向角等于颗粒的暴露角，则颗粒自重的驱动作用消失；若渗流方向角大于暴露角，则颗粒自重便成为阻碍颗粒移动的力，并随着渗流方向角的不断增大，颗粒自重的阻碍作用越来越大，直至颗粒自重完全成为阻碍力（即自重沿颗粒滚动相反方向的分力等于自重），起动所需临界水力梯度达到最大，之后伴随渗流方向角的继续增大，颗粒自重的阻碍作用逐渐减小，起动所需水力条件便逐渐降低。

4.2 相对遮挡度与相对暴露度

以sinψ表示移动颗粒的相对遮挡度，其值越大颗粒遮挡程度越低；以sinβ表示颗粒的相对暴露度，其值越大颗粒暴露程度越高。周围颗粒对临界水力梯度的影响如图7 所示。

从图7 中可以看出，移动颗粒的相对遮挡度与临界水力梯度呈正相关，即临界水力梯度随着相对遮挡度的增大而增大；而相对下游颗粒的暴露度与临界水力梯度因渗流方向的影响而呈曲线相关，随着渗流方向角的增大，临界水力梯度随着相对暴露度的增大而呈现先减小后增大的趋势。结合颗粒起动流失的理论模型分析，随着颗粒相对遮挡度的增大，驱动颗粒绕接触点滚动的拖曳力越来越小，相应地需要更大的力来克服重力力矩；随着颗粒相对暴露度的增大，一方面，驱动颗粒起动的静水压力越来越大，另一方面，随着渗流方向角的增大，自重对颗粒绕接触点滚动的驱动作用会逐渐增强或阻碍作用逐渐减弱，均导致颗粒起动临界水力梯度减小，而当渗流方向角逐渐增大至下游颗粒不再受移动颗粒自重阻碍时，自重对颗粒绕接触点滚动的阻碍作用又会随相对暴露度的增大而逐渐增强。由此可知，伴随渗流方向角的增大，颗粒起动的临界水力梯度会出现随着相对暴露度增大而先减小后增大的变化趋势。