基于改进卷积神经网络算法的违规作业行为检测

2023-11-10赵连斌张锋杨辉

电子设计工程 2023年21期

赵连斌，张锋，杨辉

（1.国网甘肃省电力公司，甘肃兰州 730000；2.国网甘肃省电力公司定西供电公司，甘肃定西 743000）

随着电力行业数字化转型的推进，对于无人值守的变电站、电力施工作业现场多采用视频球机进行远程监控，以识别电力生产参与人员的违规作业行为[1-4]。因此，提升视频识别检测的算法精度，对提升电力生产的安全管控水平具有重要意义。

当前，电力生产上使用的视频识别技术多针对于人体的行为和活动。根据视频识别理论，人体行为可分解为底层的抬手、转头、行走、奔跑等基本动作单元[5-11]。因此，需要基于采集的视频信息来提取相关的底层特征，并依据电力生产的相关规范，对相关行为进行违规判别。以卷积神经网络(CNN)为代表的深度学习算法是当前计算机领域进行视频识别的主要方法。CNN 网络通过搭建具有极强非线性拟合能力的神经网络，实现视频信息提取、分类和判别。该文针对CNN 网络的特征提取范围、训练方式等进行了改进，进一步提升了该网络的识别精度和训练效率。

1 理论基础

1.1 3D卷积神经网络

传统的卷积神经网络中主要包含卷积(Conv)、池化(Pooling)、全连接(Full Connect,FC)三种不同的连接单元，且具备良好的特征提取与表达能力，可实现二维的图像识别。其基本结构如图1 所示[12-13]。

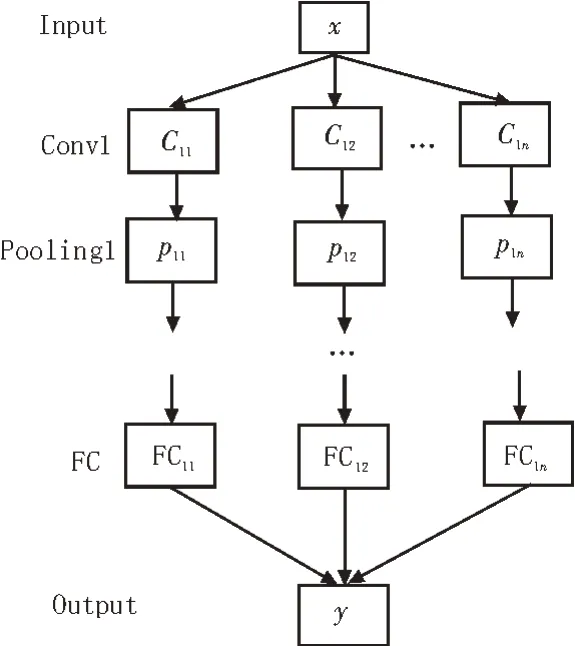
图1 CNN神经网络结构

CNN 网络通过多个神经单元组成深层次的网络，完成图像的识别与处理。但对于视频信号，其包含了时间、空间信息，传统的二维卷积运算无法满足特征提取需求，故需引入包含时间信息的3D 卷积结构。图2 给出了2D、3D 卷积结构的区别[14]。

图2 2D和3D卷积运算的对比

在图2 中，H为二维图像的高度，W为宽度，k为卷积运算的卷积核大小。

根据图2，式（1）给出了3D 卷积运算的数学表达式：

其中，Tm为视频帧的时间长度，ymn(w,h,t)为视频序列中第m层、第n个特征块在该位置的卷积输出，vmn(·)为网络的连接权重，umn(·)为该层的卷积输入，bmn为该卷积元的直流偏置。

对应于3D 卷积运算，池化运算也可以扩展到三维空间：

网络采用的是最大值池化操作，通过池化可以有效降低网络参数，提升模型训练效率。

借鉴Google 公司Inception 的改进思路，在3D 卷积层使用更小尺寸的卷积核，捕获更多的信息，从而进一步增强网络的非线性学习能力。具体方法如图3 所示。

图3 使用1×3和3×1卷积核替代3×3卷积核

1.2 C3D网络的训练方法

在CNN 网络中，权重和偏置参数的训练通常是基于随机梯度下降法(Stochastic Gradient Descent,SGD)[15-16]进行计算的：

其中，E为网络在优化时使用的误差函数，η为训练时的学习率。在使用随机梯度下降法训练时，由于学习率无法随着网络训练过程的推进动态调整，在进行三维网络训练时，导致后期训练参数更新速度降低，陷入局部最优。该文使用一种基于分数阶动量的梯度下降法进行训练(Fractional Momentum Gradient Descent,FMGD)：

其中，μ为动量的调节因子，为误差传递过程中蕴含的动量信息。为了保证训练过程中误差收敛的稳定，通常μ=0.9。取动量的γ阶差分为：

采用G-L差分公式，对式（6）进行二项展开可得：

结合式（3）对式（6）进行整理可以得到，分数阶动量的梯度下降训练下的参数更新方式：

在工程应用中，由于无法进行全量的二次项展开，因此需要引入截断机制，根据要求的计算精度进行适当的截断。在使用式（8）、式（9）进行训练时，γ可以调节动量的作用力度。当γ较小时，有利于加速网络的训练速度；当γ较大时，有利于提升训练精度。γ的取值和γmin、γmax、迭代次数m、最大迭代次数M间需满足：

2 方法实现

2.1 仿真实验设计

该文设计的仿真实验流程，如图4 所示。算法的仿真包括模型的训练与测试阶段。训练时，将视频片段、视频类别分别作为网络的输入和期望输出，使用分数阶动量随机梯度下降法进行训练。

图4 仿真实验流程

为了对算法的性能进测试，以某电力公司2020—2021 年间安全监察部门采集的电力作业现场典型违章行为视频作为模型训练和验证的数据集。该数据中包含了电力现场非法进入带电区、未戴安全帽、接地线悬挂错误、未佩戴安全绳等多个动作，且在不同的相机角度、采集光线、镜头深远等条件下进行样本采集，表1 给出了该数据集的相关参数。

表1 数据集参数

如上文所述，设计的卷积神经网络是基于3D 卷积结构，根据数据集规模，该文使用的C3D 网络结构如表2 所示。

表2 网络结构参数

为了使3D 卷积运算获取更多的信息，根据图3的方案，使用1×3 和3×1 卷积核替代3×3 卷积核。而基于分数阶动量的梯度下降法网络训练过程中所采用的相关参数设置，如表3 所示。

表3 FMGD训练参数设置

为了便于评估算法运行的时间、硬件损耗，表4给出了算法仿真时使用的计算机软硬件环境参数。

表4 算法仿真环境

2.2 仿真结果

评估基于分数阶动量网络训练方法的效率，根据表3 的训练参数设置，对5、15、20 三个不同截断长度下的模型训练效果进行了评估，具体结果如图5所示。

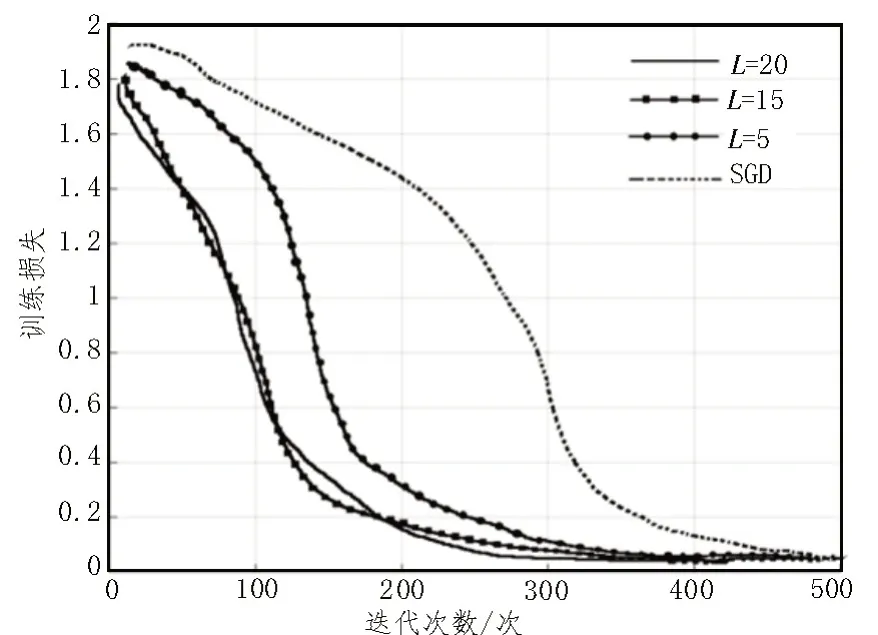
图5 网络训练效率仿真

在图5 中，还增加了传统的基于随机梯度下降(SGD)的训练方式作为对比。从图中可以看出，SGD在400 次训练后，训练损失趋于平稳；FMGD 的训练效率明显优于SGD，且其的训练效果与截断长度的取值相关。当取值为5 时，FMGD 在训练约200 次后，训练的损失趋于平稳；当取值为15、20 时，FMGD在训练约150 次后，训练损失趋于平稳。但考虑到随着截断长度的增加，训练的时间成本也会增长，故该文最终选取截断长度为15。该文以动作识别的精度作为评判模型性能的指标，算法识别指标测试结果如表5 所示。