基于改进LSTM 的电力负荷预测与成本感知优化策略研究

2023-11-10张泽龙韦冬妮唐梦媛纪强杨燕

电子设计工程 2023年21期

张泽龙，韦冬妮，唐梦媛，纪强，杨燕

（国网宁夏电力有限公司经济技术研究院，宁夏银川 750002）

当前“碳达峰、碳中和”的目标，对高耗能行业的发展提出了新的要求。因而在市场化机制下，为实现企业的可持续发展，高耗能企业面临着用能结构优化转型的巨大压力[1-3]。

现代用能企业通常利用物联网技术（Internet of Things，IoT）实现企业自身能耗情况的监测，并积累了海量的用能数据[4-5]。但对于如何利用这些数据实现用电负荷的精准预测，进而指导并合理安排生产计划，仍是亟需解决的重要问题[6-8]。

针对此问题，该文充分利用企业积累的用能数据，同时结合人工智能算法技术，研究并设计了一种基于改进长短期记忆（Long Short-Term Memory，LSTM）网络模型的电力负荷预测算法，从而为企业用电成本感知优化提供指导。

1 算法设计

1.1 循环神经网络

循环神经网络（Recurrent Neural Network，RNN）是一种具有特殊结构的神经网络，其典型结构如图1所示[9]。该网络拥有共享的拓扑结构与网络参数，同时将前一时刻的信息共享给后一时刻，能够处理时间序列数据。此外，循环神经网络在图像识别、语言交互等领域应用广泛。

图1 RNN结构

由图1 可知，Ct与ht相等，且t时刻的输出为：

式中，Wx是输入xt的权重系数，WC是上一时刻隐藏层输出Ct-1的权重系数，g为激活函数，b为偏置，et则为激活函数的输入。由式（1）可知，当前时刻隐藏层的输出Ct不仅与当前时刻的输入xt有关，还与上一时刻神经单元的状态Ct-1有关。

RNN 采用梯度下降（Gradient Descent，GD）进行参数更新，对于t时刻的输出，其与真实值之间的误差损失为：

式中，yt为t时刻的真实输出值。

以损失函数对Wx求偏导为例，计算公式如下：

RNN 常用的激活函数为tanh 函数，因此式（3）中Cj的计算公式如下：

则有：

tanh 函数导数的取值范围为[0,1]。当t取值较大时，式（3）的值便会接近于0，并导致梯度消失问题。

1.2 长短期记忆网络

RNN 由于存在梯度消失的问题，导致其无法较好地实现对长时间序列数据的处理[10]。而LSTM 是一种具有特殊结构的循环神经网络，其可适用于长时间序列数据的处理。该网络结构如图2 所示[11-13]，且循环模块即为LSTM 单元。

图2 LSTM结构

LSTM 单元的输入包括三部分：当前时刻的输入信息xt、上一时刻LSTM 单元的输出信息yt-1与LSTM 单元的状态信息St-1。

遗忘门根据xt及yt-1决定St-1信息被传递至当前时刻的数量，其表达式为：

式中，gt、Wg和bg分别为遗忘门的输出、权重系数及偏置，σ(·)则为Logistic 函数。

gt的取值范围是[0,1]，上一时刻LSTM 单元状态信息传递至当前时刻的部分为：

输入门根据xt和yt-1决定当前时刻LSTM 单元状态信息的更新部分，一方面，通过Logistic 函数通道确定更新信息的比例；另一方面，通过tanh 函数通道确定更新信息的具体内容。

式中，Wh和WS均为输入门的权重系数；bS、bh则为输入门的偏置；ht为更新信息的比例；S′t为更新信息的内容。则当前时刻LSTM 单元状态信息的更新部分为：

结合式（6）-（10），当前时刻LSTM 单元状态信息为：

输出门根据xt、yt-1与St决定LSTM 单元的输出信息，并通过Logistic 函数通道确定输出信息的比例，同时还利用tanh 函数通道确定输出信息的内容。输出信息的比例及内容计算公式，分别可表示为：

式中，Wq、bq分别为输出门的权重系数和偏置，qt、ot则分别为输出信息的比例及内容。

根据式（12）-（13）可确定当前时刻LSTM 单元的输出信息为：

2 电力负荷预测与成本感知优化

基于上述分析，该文提出了基于改进粒子群算法与随差遗忘长短期记忆时间网络的电力负荷预测与成本感知优化方法，其具体结构如图3 所示。该方法采用改进粒子群算法对LSTM 网络的超参数进行优化，利用EFFG-LSTM 网络对生产计划、历史负荷、季节、天气及温度等数据进行分析处理，从而实现电力负荷精准预测与成本感知优化。

图3 IPSO-EFFG-LSTM算法结构

2.1 改进粒子群算法

由于LSTM 网络参数的设置具有随机性，只有通过大量计算才能确定最优的参数[14]。因此为了避免无方向性地搜寻参数，该文采用粒子群算法对LSTM网络的隐藏层数、学习率及迭代次数等进行优化。

在t+1 时刻，粒子位置xt+1和速度vt+1的更新机制如下：

式中，rt为粒子最优位置；bt为种群最优位置；κ1和κ2为加速度系数；λ1和λ2为随机数，且满足0 ＜λ1＜1 和0 ＜λ2＜1；μ为惯性系数。

传统PSO 算法的惯性系数μ通常设置为定值。当μ取值较大时，算法的全局搜索能力强，但局部搜索能力较差；而当μ取值较小时，算法的求解速度较慢，且易陷入局部最优解[15-16]。

为了平衡算法的全局与局部搜索能力，文中对传统PSO 算法进行改进。采用自适应的惯性系数，其计算方式如下：

其中，μmax与μmin分别为惯性系数取值范围的上下界，h为粒子的适应度值，havg和hmin则分别代表粒子种群适应度平均值及最小值。

2.2 随差遗忘LSTM

LSTM 单元内的遗忘门决定上一时刻信息对当前时刻预测结果的影响。在企业生产过程的电力负荷预测与成本感知中，进行t时刻电力负荷预测时，若已知t-1 时刻电力负荷的实际值，可利用该时刻电力负荷预测的偏差优化调整上一时刻信息对当前时刻预测的影响程度。若偏差较大，说明上一时刻预测不准确，故其对当前时刻的预测并无较大的支撑作用，需减少上一时刻信息对当前预测的影响；反之，则要增加上一时刻信息的影响。

基于此，该文对传统LSTM 的遗忘门进行改进。同时考虑到由于Logistic 函数的导数小于1，易出现梯度消失现象。因此，将传统LSTM 单元中的Logistic函数改进为ReLU 函数。改进后的LSTM 单元结构如图4 所示。

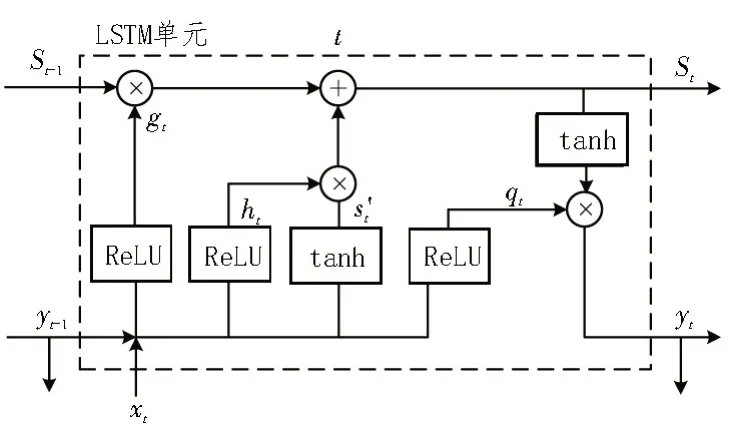
图4 随差遗忘LSTM单元结构

基于误差跟随的遗忘门可描述为：

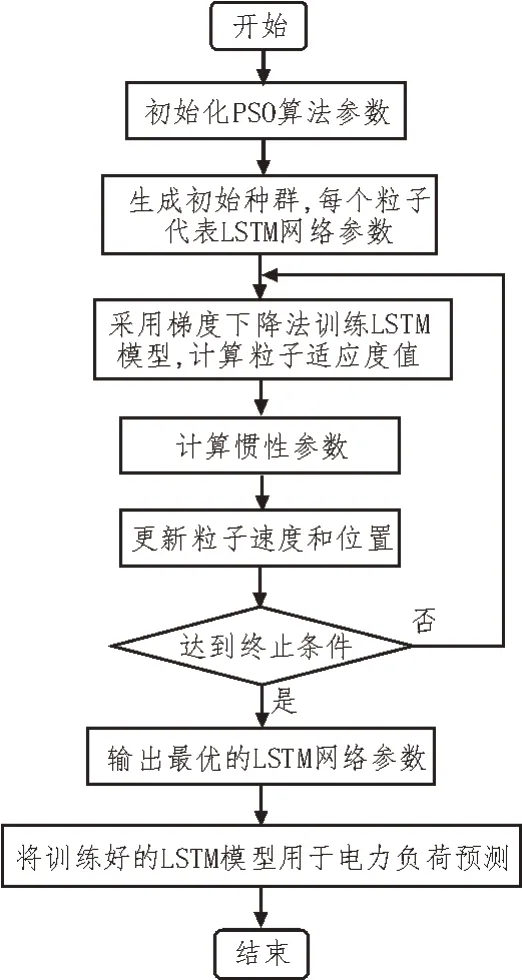
图5 IPSO-EFFG-LSTM算法流程

2.3 用电成本优化模型

在实现电力负荷预测的基础上构建企业用电成本优化模型，具体可表征为：

式中，F为目标函数，即企业用电成本；和Pt分别为t时段优化前后的企业预测用电负荷；ct为t时段电价；Δt为时间间隔；为优化关闭第k种生产设备的台数，Pk为第k种生产设备运行功率；则为原计划运行第k种生产设备的台数。

3 算例分析

文中结合某企业的历史电力负荷以及从气象系统获取的季节、天气与温度等信息来构建输入样本集，且样本总数为2 080 条。

3.1 电力负荷预测结果分析

为对比分析该文所提算法与LSTM、EFFGLSTM 算法的性能，并将相同训练样本集作为输入数据，对神经网络模型加以训练。同时，采用测试集对训练好的LSTM 模型进行测试。不同算法的评价指标对比如表1 所示。

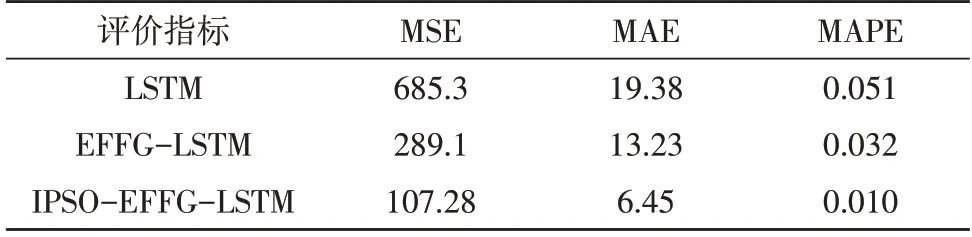
表1 不同算法电力负荷预测误差

从表中可以看出，LSTM 算法预测精度最差，EFFG-LSTM 算法相比LSTM 算法在预测精度上具有较大的提升，而所提算法的预测结果更为准确。

同时，将训练好的神经网络模型应用于该企业某日的电力负荷预测，结果如图6 所示。由图可知，LSTM 算法与真实负荷值的差距较大，且平均预测误差大于10%。而EFFG-LSTM 算法则在LSTM 的基础上，针对遗忘门进行改进，进而提高了算法的动态特性，故电力负荷曲线拟合效果较优，平均预测误差约为7.9%。该文算法则在EFFG-LSTM 算法基础上，又引入了IPSO 算法以解决LSTM 网络参数选取随机性较大的问题，从而实现了LSTM 网络参数的最优选取，并大幅提高了电力负荷预测的准确性，且其平均预测误差仅为5.2%。