基于DBN-RF 的配电网多能互补优化调度算法

2023-11-10汤俊峰

电子设计工程 2023年21期

汤俊峰

（国网浙江省电力有限公司龙泉市供电公司，浙江龙泉 323700）

在电力系统中，配电网的能源管理至关重要，调度方案的优劣直接决定了配电网能否安全、稳定地运行。配电网络中控制单元的数量较多。因此，合理地规划控制单元启动、停止和输出，并对其进行协调和优化是目前国内外相关领域的重要研究课题。

常规配电网以火电、水电、核电为主要动力来源，其输出稳定、可控。由于风电、光伏出力预测的准确性不高，因此必须充分考虑配电网的随机性和波动性。倪识远[1]等人提出了一种考虑动态重构的调度方法，该方法通过使用环路网架十进制编码方式，能够为模型上下层决策变量提供电源出力。定义相同目标函数上下层决策变量，使用协同优化策略进行配电网主动最优调度。叶亮[2]等人提出了基于最优潮流的调度方法，运用二阶锥松弛技术构建潮流规划模型，并调用Gurobi 求解器进行求解。以优化的联络线功率为约束条件，构建配电网内可控电源调度模型，结合Tent 映射混沌技术求解调度结果。调度优化所得的决策方案使其能够抵抗调度参数波动变化，但与此同时也意味着这两种方法的保守性较强。

由于当配电网中含有储能设备、需求响应以及电气机组等各种能量时，调度过程的约束调节过程就会更加复杂。为此，结合深度置信网络-随机森林算法(Deep Belief Networks-Random Forest,DBN-RF)进行配电网多能互补优化调度。

1 基于DBN 的配电网多能互补优化调度

研究对象为配电网分布式电机、燃气轮机组、分布式光伏机组，基于DBN 的多能互补耦合协调结构如图1 所示。

图1 深度置信网络多能互补耦合协调结构

由图1 可知，充分考虑风电与光伏出力不确定原因，结合耦合协调结构改变配电网中能量分布情况[3]，以应对不确定变量下恶劣场景预测值与真实值的偏差。

1.1 构建调度模型

电-气-热多能互补鲁棒优化调度模型是以配电网运行成本最小为目标的，充分考虑储能设备和多能耦合设备的联合运维费用，构建调度模型如式（1）所示：

式中，Z电、Z气、Z热分别表示分布式电机、燃气轮机组、分布式光伏机组发电费用；W电(t)、W气(t)、W热(t)分别表示t时段分布式电机、燃气轮机组、分布式光伏机组发电平均功率；Z本、W本(t)分别表示t时段配电网接收到的售电电价、送电平均功率[4-6]，T表示总调度时间。针对该模型设置约束条件，如式（2）所示：

1.2 模型求解

由于DBN 深度置信网络是由神经网络层和受限玻尔兹曼机层组成的，所以在使用该网络求解模型时，可以将其视为一个特征学习模型[10-11]。在该模型中，输入配电网电-气-热互联数据，针对最优调度问题，寻找电-气-热能源配电网最优日前调度方案，并给出了鲁棒优化模型下限[12]。

假设DBN 中每个受限玻尔兹曼机具有二进制可视单元和隐藏单元，将以配电网运行成本最小为目标的调度结果代入求解过程中，通过独立特征学习不会受到非线性回归过程影响。

在当前调度模式下，求取恶劣场景下多能互补耦合协调调度方案，并给出关键问题的反馈。在此基础上，将问题目标函数值与反馈问题函数值之和作为鲁棒优化模型新的上界[13]。

DBN 网络将各个层次的单元连接起来，利用无监督学习方法获得初始参数，确保模型在训练过程中不会陷入局部最佳状态[14]。在DBN 网络中，每一层信息都是由神经元数目来决定的。在信息传递过程中，为了确保信息的一致性，可将隐藏层的信息表示为式（3）：

式中，I可表示可视层的实际信息量；m表示隐藏单元数量；n表示可视单元的数量。

在确保信息量一致的情况下，判定调度模型函数的上下界。当上下界的值小于设定阈值时，算法停止迭代，此时的调度方案为最优调度方案[15]；反之，由该问题所产生的关键情景会代替该问题，并不断进行迭代求解，直至达到设定的收敛条件为止。

2 基于RF的总体协调度评价

使用RF 随机森林算法构建多能互补调度综合评价模型，该模型的关键环节是样本集的抽样，并结合所有抽样结果形成子决策树。以子决策树为基础，对调度方案进行筛选，选择最优方案作为多能互补优化调度方案。

2.1 总体协调度评价函数构建

根据基于DBN 的配电网多能互补优化调度方案，从原始样本集中抽取多个子样本集，形成子决策树。对于样本集的子决策树，计算样本集的信息熵，信息熵可表示为式（4）：

式中，Pi表示样本集x中第i类分类结果所对应的样本占比。对所有样本进行处理后，将属性节点加入决策树中，即可构建子决策树[16]。统计子决策树输出结果，在多能互补优化调度问题中，最理想的状态是满足所有单一目标均达到理想值。然而，各个目标函数都存在着矛盾，难以在满足函数的最优条件下实现。因此，需要构建一个能使各个目标函数协调一致的数值，具体计算过程如式（5）所示：

式中，R1(x)、R2(x)、R3(x)分别表示电能、气能、热能调度函数的最理想值。在这个调度过程中寻找一个决策向量x，使其表示与理想函数值最接近。因此，确定总体协调度评价函数，可表示为式（6）：

式中，R′(x) 表示综合目标函数值。在此基础上，以欧氏距离为矢量空间，对其进行综合评估。

2.2 多能互补调度综合评价

对于基于DBN 的配电网多能互补优化调度模型，求出单个目标函数的最优值，再求出每个目标的满足度函数，并在全局解空间内求出最接近最优解的最佳方案，从而获取最佳调度结果。基于RF 随机森林算法的求解步骤如下：

将多目标决策问题转换成单一目标最优问题，其表达式如式（7）所示：

式中，、T1分别表示电能总理想值和综合函数值；、T2分别表示光能总理想值和综合函数值；、T3分别表示热能总理想值和综合函数值。

利用RF 随机森林算法进行求解计算，确定最终评价结果。结合深度置信网络多能互补调度方案，确定整个配电网最佳运行模式。

3 实验与分析

3.1 实验架构

以电-气-热联供型配电网为研究对象，其结构如图2 所示。

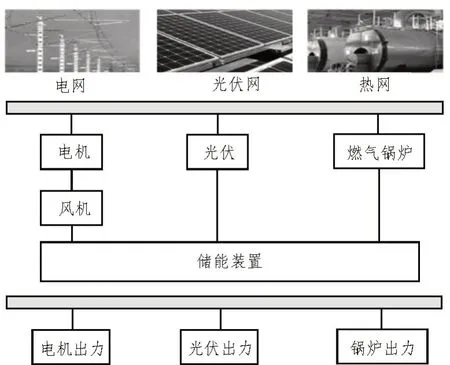
图2 电-气-热联供型配电网结构

由图2 可知，配电网主要由分布式风力发电机、分布式光伏和小型燃气锅炉组成，这些组件都是以洁净能源为动力运行的，且燃气锅炉机组对配电网的净负载变化有较强适应性。

3.2 优化调度数据分析

设置了以下四种调度场景进行对比，分析不同运行模式下调度算法的经济性。四种场景分别是：

场景1：电机-光伏联合运行，不考虑燃气锅炉，配电网常规调度。

场景2：电机-燃气锅炉联合运行，不考虑光伏，配电网常规调度。

场景3：光伏-燃气锅炉联合运行，不考虑电机，配电网常规调度。

场景4：电机-光伏-燃气锅炉联合运行，配电网常规调度。

四种场景下配电网调度结果如表1 所示。

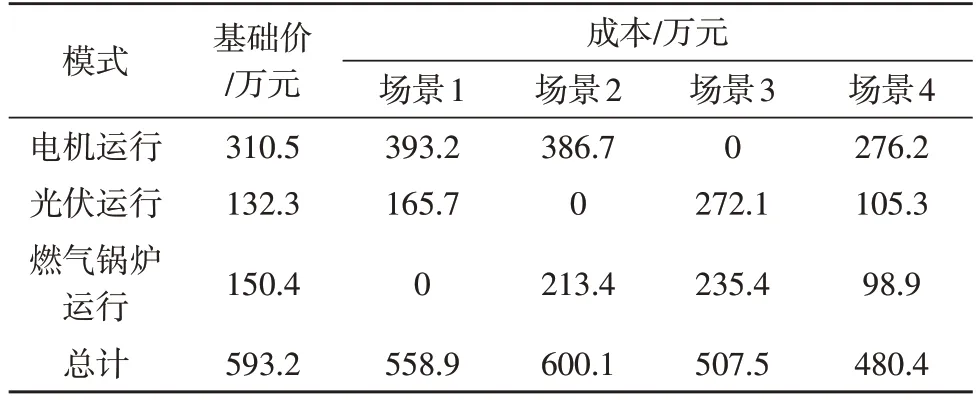
表1 四种场景下配电网调度结果

场景1：当电机、光伏机组作为一个整体接入配电网时，这两部分能源的日前调度总成本相对于基础价有所增加，这是因为配电网为应对不确定变量，大幅度增加配电网的购电、光伏利用行为，其中购电行为在达到用电负荷后，剩余部分主要供给燃气锅炉出力，转换为更多热能。

场景2：当电机、燃气锅炉作为一个整体接入配电网时，大幅度增加配电网的购电、购气行为，其中购电、购气行为在达到用电、用气负荷后，剩余部分主要供给光伏机组出力。

场景3：当光伏、燃气锅炉作为一个整体接入配电网时，这两部分能源调度总成本大幅度增加，通过配电网光伏利用、购气行为，将剩余部分供给电机出力，转换为更多电能。

场景4：当电机、光伏机组、燃气锅炉作为一个整体接入配电网时，这三个部分的调度总成本相对于基础价有所减少，其原因是当电机、光伏机组在恶劣情况下使出力达到最大值时，燃气锅炉可停止运行。同理，电机、光伏机组在出力充裕情况下，配电网在一定程度上提升了消纳能源的能力，保证配电网调度成本最低。

3.3 实验结果与分析

为了进一步验证基于DBN-RF 的配电网多能互补优化调度算法应用的合理性，将其与考虑动态重构的调度方法、基于最优潮流的调度方法进行实验对比分析。三种方法配电网出力的输出有功功率情况如图3 所示。

图3 三种方法配电网出力对比分析

由图3 中所示的实验结果可以看出，使用考虑动态重构的调度方法在10 h 时，与理想出力数据存在最大误差，最大差值为90 kW；使用基于最优潮流的调度方法在10 h 时，与理想出力数据存在最大误差，最大差值为40 kW；使用基于DBN-RF 的调度方法与理想出力数据一致。上述结果说明基于DBNRF 的配电网多能互补优化调度算法的应用效果较为理想，能够有效提升配电网消纳能源的能力，提高整体的调峰效益。