基于机器视觉的无人机自动巡检定位控制技术

金涛，黄俊波，蔡澍雨，龚明义，谢程

（云南电网有限责任公司输电分公司，云南昆明 650051）

机器视觉是指利用机器设备来代替人眼对待测物行进状态进行判断，在主机元件的作用下，所有测量信号都会以数据信息的形式反馈给各级应用设备，一方面实现了对传输信号的无误转换；另一方面也可以将数字化信息完整转存于主机元件之中[1-2]。对于一些不适合人工作业的危险场合而言，以机器视觉代替人工视觉，不但能够实现对待测物的有效控制，还可以将信号参量直接转化成数据信息，以供处理主机直接调取与利用。在实际应用过程中，机器视觉理论的实现需要云端电脑、影像摄影机、影像显示器、伺服运动平台等多个设备元件的共同配合。

无人机自动巡检是指利用无人机飞行器，对行进区域内的行进线路环境进行自动探查，一般来说，与不同行进区域匹配的巡检节点布局形式也会有所不同[3]。由于无人机巡向角过度偏转问题的存在，巡检节点的实际布局形式并不能完全符合初始定位需求，这也是导致无人机飞行器不能按照预设路线行进的主要原因。为避免上述情况的发生，有学者提出基于Cascade R-CNN 的检测算法，利用位姿传感器记录无人机飞行器的实际行进路径，再根据既定算法原则，确定巡检节点之间的分布配比关系[4]。然而该方法的执行能力有限，并不能完全满足实际应用需求。为解决该问题，引入机器视觉理论，并以此为基础，设计一种新型的无人机自动巡检定位控制方法。

1 基于机器视觉的无人机巡检节点抓取

基于机器视觉理论的无人机巡检节点抓取包含巡检坐标变换、正运动学方程求解、逆运动学方程求解三个处理流程，具体研究方法如下。

1.1 巡检坐标变换

对于无人机飞行器而言，坐标变换原则能够同时满足机器视觉理论与巡检定位控制的执行需求[5-6]。规定点O为无人机巡检曲线的起始点，其物理坐标为(0,0,0)，点R1为一个随机选取的巡检轨迹节点，其物理坐标为(x1,y1,z1)。可将点O与点R1之间的间隔距离L1表示为：

设θ1表示横纵坐标之间的物理夹角，θ2表示纵坐标与空间坐标之间的物理夹角，θ3表示横坐标与空间坐标之间的物理夹角。联立公式（1），可将基于机器视觉的无人机巡检坐标变换原则表示为：

在机器视觉理论的认知中，物理坐标轴之间的夹角数值越大，表示所选取巡检节点与起始点之间的物理间隔距离越大，此时巡检坐标系中能够保持对应变换关系的定位节点数量也就越多。

1.2 正运动学方程求解

正运动学方程求解是无人机巡检节点抓取处理过程中的关键执行步骤，可在已知巡检坐标变换条件的基础上，计算无人机飞行器在单位运动区域内的实时行进能力[7-8]。假定v1表示无人机飞行器的匀加速行进速率，此时巡检路径内的实时加速度为a1，v2表示无人机飞行器的匀减速行进速率，此时巡检路径内的实时加速度为a2。设β表示机器视觉作用对于无人机巡检运动行为的影响系数。联立上述物理量，可将基于机器视觉的无人机飞行器正运动学方程求解结果表示为：

1.3 逆运动学方程求解

逆运动学方程求解也是无人机巡检节点抓取处理过程中的必要执行步骤，作为正运动学方程求解的反向运算过程，能够约束无人机飞行器的匀减速运动状态[9-10]。设表示无人机飞行器在匀减速巡检过程中的运动功率均值，且≥1 的不等式条件恒成立。χ、δ表示两个不同的逆运动系数，指标χ的物理取值也始终大于指标δ。规定φ表示基于机器视觉理论的无人机逆向运动参量，联立上述物理量，可将基于机器视觉的无人机飞行器逆运动学方程求解结果表示为：

其中，ΔE表示无人机飞行器在单位时间通过的巡检区域面积。逆运动学方程与正运动学方程的作用能力相同，但后者只能直接影响无人机飞行器在匀减速运动过程中的行进状态。

2 无人机自动巡检的定位与控制方法

2.1 特征点提取

设μ表示既定的无人机自动巡检系数，k1、k2、…、kn表示n个不同的巡检特征点指标，i表示最大的巡检路径定位参量，f表示基于机器视觉理论的无人机巡检节点控制权限量值[11-12]。在上述物理量的支持下，联立式（3）、式（4），可将基于机器视觉的无人机自动巡检特征点提取表达式定义为：

对于后续的巡检曲线定位权限原则而言，特征点提取将无人机巡检节点限定在了一定的区域范围之内，使得控制主机具备了准确估量无人机巡向角偏转行为的能力。

2.2 帧间位姿估计

设ω表示一个随机选取的无人机巡检帧节点定义系数，该项指标参量的最小取值结果只能等于自然数1，lω表示节点定义系数等于ω时的无人机巡检位姿行为向量，且lω＞0 的不等式条件恒成立[13-14]。在上述物理量的支持下，联立式（5），可将无人机帧间位姿估算表达式定义为：

2.3 巡检曲线定位权限

巡检曲线定位权限决定了主机元件对于帧间节点的控制能力，一般来说，权限量表达式的取值结果越大，表示主机元件对于帧间节点的控制作用能力越强[15-16]。设z1、z2、…、zn表示无人机巡检路径中n个不同的曲率系数，ξ表示巡检节点的定位特征参量，u表示可行性系数，υ表示无人机巡检路径中的曲率标记度量值。在上述物理量的支持下，联立式（6），可将基于机器视觉的无人机巡检曲线定位权限表达式定义为：

至此，实现对各项指标参量的计算与处理，在不考虑其他参考条件的情况下[17-19]，完成针对基于机器视觉的无人机自动巡检定位控制技术的研究与分析。

3 实例分析

利用moc studio2.0 v2.63 软件对无人机巡检运动的视觉图像进行模拟（如图1 所示），调节各项指标参数，将无人机巡检范围控制在一个5 km×5 km的正方形区域内。

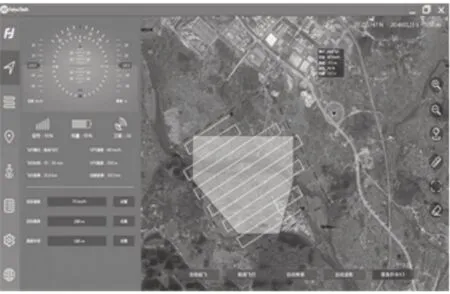
图1 无人机巡检运动的模拟视觉图像

将所选巡检区域划分成四部分，并分别对其标号为1、2、3、4（如图2 所示），且每一部分的边长值水平完全相等。首先利用基于机器视觉理论的应用方法对无人机巡检运动进行控制，将所得数据作为实验组变量；然后利用基于Cascade R-CNN 的检测算法对无人机巡检运动进行控制，将所得数据作为对照组变量；最后对实验组、对照组变量数值进行对比。

图2 无人机巡检区域划分

实验以无人机巡向角偏转度数作为参考变量。一般来说，当巡向角偏转度数处于0°～95°的数值区间时，表示控制主机对于巡检节点的定位能力较强，当前巡检节点的布局形式也就更符合实际应用需求；若巡向角偏转度数超过95°，则表示控制主机对于巡检节点的定位能力相对较弱。

图3 反映了无人机飞行器在4 个巡检区域内的巡向角偏转度数变化情况。

图3 巡向角偏转曲线

在1 号区域中，实验组无人机巡向角偏转度数保持来回波动的变化状态，全局最大值仅能达到79.8°，低于理想极限值95°；对照组无人机巡向角偏转度数保持先上升、再下降的变化状态，全局最大值达到了110.8°，高于理想极限值95°。

在2 号区域中，实验组、对照组无人机巡向角偏转度数均呈现出不断增大的变化状态，前者最大值为84.7°，低于理想极限值95°，后者最大值为110.4°，高于理想极限值95°。

在3 号区域中，实验组无人机巡向角偏转度数呈现先大幅上升、再小幅下降、最后基本稳定的变化状态，全局最大值仅能达到78.6°，低于理想极限值95°；对照组无人机巡向角偏转度数呈现先大幅上升、再不断波动的变化状态，全局最大值为108.9°，高于理想极限值95°。

在4 号区域中，实验组无人机巡向角偏转度数保持阶段性上升的变化状态，全局最大值为75.7°，低于理想极限值95°；对照组无人机巡向角偏转度数保持先上升、再波动、最后继续上升的变化状态，全局最大值达到了113.5°，高于理想极限值95°。

综上，在基于机器视觉理论的应用方法的作用下，无人机飞行器在各个行进区域内的巡向角偏转度数值均处于0°～95°的数值区间，表示控制主机对于巡检节点的定位能力始终较强。

4 结束语

在机器视觉理论的作用下，无人机自动巡检定位控制方法针对巡向角过度偏转的问题进行改进，根据已知的巡检坐标变换原则，得到准确的正、逆运动学方程求解结果，又利用各个特征点提取指标，定义帧间位姿的计算表达式，从而得到巡检曲线定位权限指标的具体数值。随着基于机器视觉理论的控制方法的应用，无人机飞行器的巡向角偏转度数值得到了较好控制，巡检节点布局形式更符合实际定位需求。