UFMC 系统基于改进离散粒子群的峰均比抑制算法

陈 雷，刘海洋，郝玉莲，刘帅奇，张锁良

(河北大学电子信息工程学院，河北 保定 071000)

现行的正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术由于本身的固有特性，在适应新一代移动通信技术的业务需求时存在明显的缺陷［1］。主要表现为：

（1） 子载波必须保持正交，对频率偏移敏感性高，需要严格的时频同步；

（2） 存在较大的载波间干扰，需要插入循环前缀，使得频谱效率下降；

（3） 子载波占用带宽恒定，在短包数据通信业务上缺乏灵活性。

针对OFDM 存在的上述缺陷，学界提出几种新型多载波技术来适配下一代移动通信技术的业务需求［2－4］。其中，通用滤波多载波（Universal Filtering Multi-Carriers，UFMC）凭借更高的频谱效率、更低的带外泄露、更灵活的子带配置被认为是面向B5G 和6G 的一种有力的候选波形技术。相较于滤波OFDM（Filter-OFDM，F-OFDM） 技术，UFMC 可以摆脱循环前缀对频带资源的占用，提高频谱效率；相较于滤波器组多载波（Filter Bank Multi-Carrier，FBMC）技术，UFMC 可以选用长度更短的滤波器，降低实现的复杂度；并且由于未采用偏移正交振幅调制（Offset Quadrature Amplitude Modulation，OQAM）技术，UFMC 更易与多入多出（Multiple-Input Multiple-Output，MIMO）技术相结合［5－7］。

由于采用多载波技术，需要面临同向相位信号叠加而导致的峰均比（Peak-to-Average Power Ratio，PAPR）过高问题，这使得高功率放大器（High-Power Amplifier，HPA）无法工作在线性放大区，对信号的传输产生一定程度的影响，最终导致误码率（Bit Error Rate，BER）增加［8］。理论上，在高峰均比的场景下，线性工作范围更大的HPA 仍可以正常工作，但这种解决方案会使HPA 的实现复杂度和成本进一步增加，不利于新一代移动通信技术的应用推广。因而，学界对多载波技术的重点研究方向之一正是峰均比抑制算法［9］。

文献［10］提出一种分段非线性压扩方案，将信号按幅度大小分成3 段，对每段信号采用不同的压扩策略，同时保持压扩前后信号功率和相位不变。仿真结果表明，该方案相较于经典压扩方案具有更低的峰均比；文献［11］提出一种线性非对称压扩变换方案，在发送端对大幅度信号进行压缩，对小幅度信号进行扩张，在接收端进行相应的逆操作。仿真结果表明，在高阶QAM 调制场景下，所提方案相较于经典压扩方案具有更好的峰均比抑制能力和误码率性能。文献［12］提出了一种基于DFT 预编码和非线性压扩相结合的峰均比抑制方案，该方案相较于单独采用压扩技术或预编码技术的UFMC 系统，具有更低的PAPR，但这种编码类方案会导致UFMC系统的复杂度增加。

文献［13］提出了一种采用低复杂度部分传输序列（Partial Transfer Sequence ，PTS）的方案，该方案利用相位加权序列间的关系减少了复数乘法的计算次数，在有效抑制UFMC 系统峰均比的同时，降低了部分传输序列的计算复杂度；文献［14］提出了一种基于固定功率门限的多级PTS 算法，同时兼备多级寻优PTS 技术和功率门限PTS 技术的性能特点。仿真结果表明，该算法的复杂度相较于传统PTS 技术、多级寻优PTS 技术和功率门限PTS 技术均有一定程度的下降；文献［15］将多点交叉技术和自适应参数引入遗传算法（Genetic Algorithm，GA），并与选择性映射（Selective Mapping，SLM）相结合抑制UFMC 系统中的峰均比。仿真结果表明，该算法可以有效抑制UFMC 系统中的峰均比，但计算复杂度仍然较高。

已有研究中，多数采取信号畸变类或信号编码类方案来抑制UFMC 系统的峰均比的方案，虽然也能取得一定的峰均比抑制效果，但在无失真传输和编码复杂度方面存在着明显的不足；少数基于信号加扰技术的方案，也面临着遍历寻优造成的计算复杂度过高问题。本研究采用传统PTS 技术保障峰均比抑制过程中的无失真传输，并引入智能优化算法解决该方案复杂度较高的问题，代替传统PTS 技术遍历寻优的搜索方式，发挥优化算法在寻优问题上的优势。又因为粒子群算法（Particle Swarm Optimization，PSO）具有易于实现、控制参数少等优势，所以，考虑将改进后的离散粒子群算法（Improved Discrete Particle Swarm Optimization，IDPSO）和传统PTS 技术相结合，应用到UFMC 系统中进行峰均比抑制。

1 UFMC 系统峰均比

在UFMC 系统中，首先将整个频带划分成B个子带，每个子带包含Ki个连续的子载波；然后将每个子带补零到N点并进行IFFT 运算，得到每个子带对应的时域信号xi（n）

其中，n＝0，1，…，N－1。随后，每个子带对应的时域信号xi（n） 经过长度为L的切比雪夫滤波器fi（n），此时得到的B个信号再叠加得到UFMC 的发射信号x（n）

其中，n＝0，…，N＋L－1。

UFMC 系统的发送端原理图如图1 所示。

图1 UFMC 发送端原理图

在多载波系统中，由于IFFT 运算而产生同向相位信号的叠加会导致峰均比过高，其表达式为

已有研究表明，计算多载波系统的峰均比时，选用4 倍的采样率所造成的误差可以忽略不计［8］。这里取过采样率J＝4，采样后得到的时域信号样本个数为JN，再经过长度为L的切比雪夫滤波器，所得时域信号样本个数为JN＋L－1，可得离散时间信号s（n） 的PAPR 为：

由于多载波系统的PAPR 是一个随机变量，通常使用互补累计分布函数（Complementary Cumulative Distribution Function，CCDF）来表示系统中多载波符号超过特定门限值的概率，其表达式为

其中，PAPR0表示峰均比门限值，JN＋L－1 表示时域样本信号的数量。

2 本文算法

2.1 部分传输序列

部分传输序列技术通过对每个子块进行加扰的方式来抑制多载波系统的峰均比，具体操作流程如下：

首先，将N个符号的输入数据分割成V个连续分布、大小相同的子块

然后，用相应的相位因子bv乘以每个子块，相位因子的表达式为

其中，v＝1，2，…V，ϕ∈［0，2π）。

再对已加扰的信号进行IFFT 操作，得到

最后，选择使得PAPR 最小的相位因子组合，表达式为

其中，arg min（·） 表示取得全局最小值的判决条件。

此时，最小PAPR 向量的时域信号可以表示为

由式（7）可知，ϕ在区间［0，2π）内可取任意值，使得PTS 技术在遍历搜索过程中会产生较高的计算复杂度，为简化计算复杂度，通常取则相位因子bv＝｛±1，±j｝，可将其映射为｛（0，0），（0，1），（1，0），（1，1）｝。即，将寻优搜索问题的搜索范围从连续空间简化为离散空间［16］。

PTS 技术框图如图2 所示。

图2 PTS 技术原理图

2.2 离散粒子群算法

粒子群算法是受鸟类捕食行为启发提出的一种群体智能优化算法，各个粒子同时受自身惯性、个体历史最优、群体历史最优这3 部分因素的影响，不断调整飞行速度和位置，在规定迭代次数内搜索全局最优解［17－18］。

在2.1 节，采用PTS 技术抑制UFMC 系统峰均比时，搜索范围已从连续空间简化为离散空间，因而这里也需要采用离散粒子群算法（Discrete Particle Swarm Optimization ，DPSO）进行寻优搜索。离散粒子群算法是在粒子群算法的基础上通过引入sigmoid 函数进行离散化处理，实现对离散空间最优解的搜索［19］。离散粒子群算法的函数表达式为

其中，sigmoid（vi（t＋1））＝，w表示惯性权重，c1、c2为学习因子，分别表示认知因素和社会因素，vi（t） 表示第i个粒子t时刻的速度，vi（t＋1）表示第i个粒子t＋1 时刻的速度，wi（t） 表示第i个粒子t时刻的位置，wi（t＋1） 表示第i个粒子t＋1时刻的位置，wipbest（t） 表示第i个粒子t时刻的最优搜索位置，wgbest（t） 表示所有粒子群体t时刻的最优搜索位置，rand 表示在区间（0，1）内均匀分布的随机数。

离散粒子群算法在寻优过程中需经过如下步骤：

（1） 粒子群体初始化，每个粒子获取一个随机的初始速度和位置；

（2） 计算每个粒子的适应度值；

（3） 计算每个粒子、全部粒子群体的历史最优值；

（4） 根据式（11）、式（12）更新粒子自身的速度和位置；

（5） 若不满足终止条件，重新进入步骤2；若满足终止条件，则输出最优的搜索结果。

离散粒子群优化算法的流程如图3 所示。

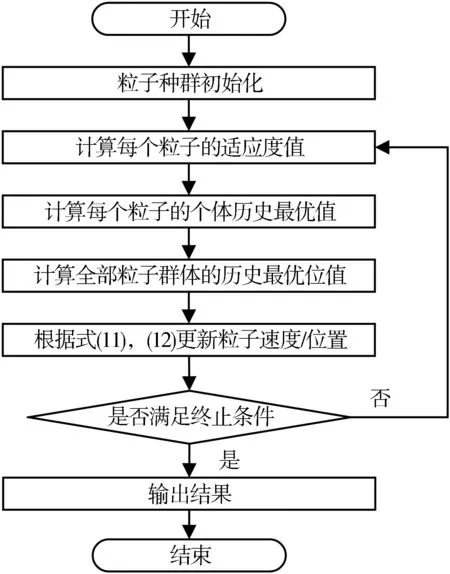
图3 离散粒子群优化算法流程图

2.3 改进离散粒子群算法

由于传统离散粒子群算法存在难以收敛到全局最优的缺陷［20］，针对这一问题，本研究在平衡离散粒子群算法全局搜索能力与局部搜索能力的前提下，在式（11）中引入一种对控制参数分段线性调整的改进方式。在搜索前期，为增加全局搜索能力，惯性权重w和学习因子c1需要保持一个较大的值；在搜索后期，为了收敛到全局最优，惯性权重w需要保持一个较小的值，而学习因子c2需要保持一个较大的值。其表达式如下

其中，wmax＝0.9，wmin＝0.4；cmax＝2.5，cmin＝0.5；α表示函数分段点的归一化取值。

改进前后的主要控制参数惯性权重w、学习因子c1和学习因子c2变化趋势分别如图4、5 所示。

图4 惯性权重随迭代次数变化示意图

图5 学习因子随迭代次数变化示意图

2.4 IDPSO-PTS 算法

2.4.1 基本原理

将2.1 节中的PTS 技术和2.3 节中的IDPSO 算法相结合得到IDPSO-PTS 算法对UFMC 系统进行峰均比抑制。

在IDPSO-PTS 算法中，首先将发送端的频域数据分成V个子块，再对每个子块分别进行N点IFFT运算，然后经过长度为L的切比雪夫滤波器处理，最后与IDPSO-PTS 算法搜索得到的最优相位选择因子组合相乘相加，并计算出最小的PAPR 值。IDPSO-PTS 算法流程如图6 所示。

图6 IDPSO-PTS 算法流程图

2.4.2 计算复杂度

对传统PTS 技术和IDPSO-PTS 算法进行复杂度分析。为简化计算，将复数比较运算等价为复数加法运算［14］。传统PTS 技术遍历搜索的相位因子组合个数为WV－1，时域样本数量为JN＋L－1，由式（8）和式（9）共产生WV－1∗（JN＋L－1）∗V次复数乘法和2∗WV－1∗（JN＋L－1）∗V－1 次复数加法。同理，在IDPSO-PTS 算法中，搜索的相位因子组合个数为P∗T，时域信号的样本数量为JN＋L－1，由两式共产生P∗Τ∗（JN＋L－1）∗V次复数乘法和2∗P∗T∗（JN＋L－1）∗V－1 次复数加法。

根据上述表达式可知，峰均比抑制算法的计算复杂度主要受种群个数P、最大迭代次数T和相位因子个数W以及子块数目V的影响。当相位因子组合个数较小时，PTS 技术可以实现对峰均比的有效抑制；而当相位因子组合个数较大时，PTS 技术的计算复杂度随着子块数目V的增加呈指数增长，不再适用于UFMC 系统的峰均比抑制；而IDPSOPTS 算法的计算复杂度与种群大小P和最大迭代次数T的乘积成正比，具有更低的计算复杂度，仍然适用于UFMC 系统的峰均比抑制。

3 仿真实验

为评估本文所提IDPSO-PTS 算法与其他相关算法在UFMC 系统中进行抑制峰均比的性能差异，选用如表1 所示参数在MATLAB 中进行仿真测试。

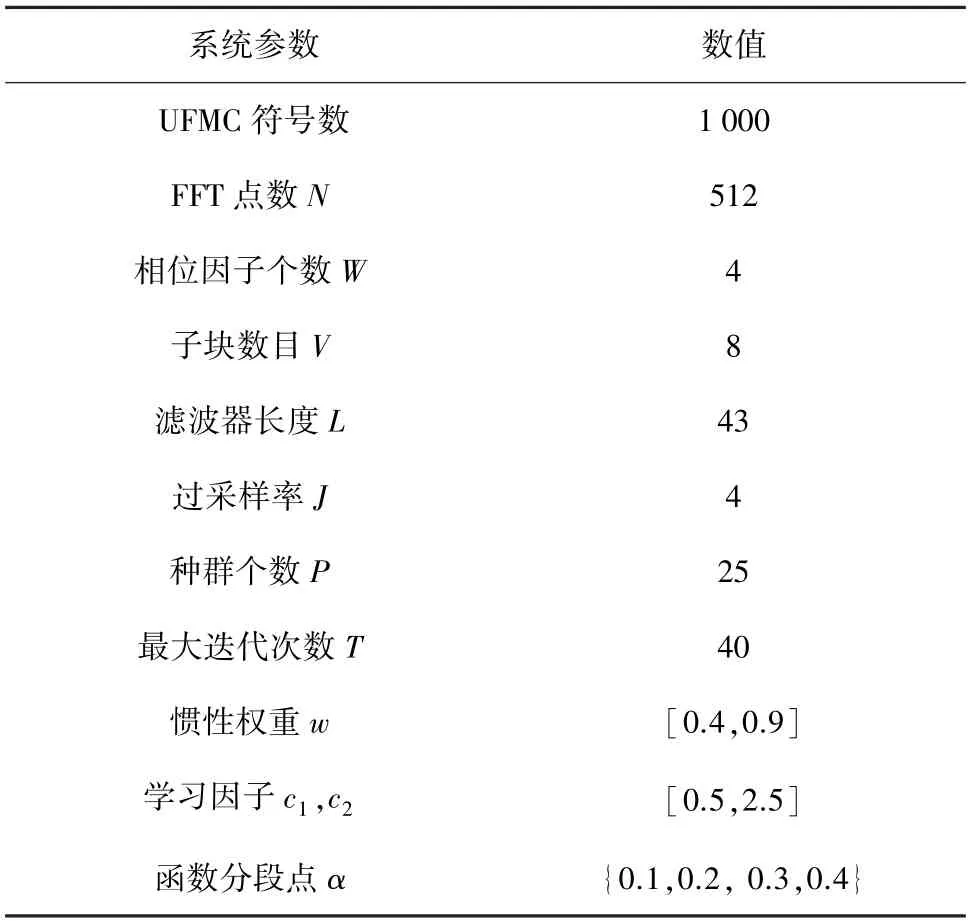
表1 仿真参数表

为验证IDPSO-PTS 算法的峰均比抑制能力，分别同原始UFMC、DPSO-PTS 算法、传统PTS 技术相比较。

不同算法的峰均比抑制效果如图7 所示，若取CCDF＝10－3，原始UFMC 的PAPR 为11.2 dB，DPSO-PTS 算法的PAPR 为7.9 dB，IDPSO-PTS 算法的PAPR 为7.7 dB，传统PTS 技术的PAPR 为7.6 dB。各算法较原始UFMC 系统的峰均比抑制能力提升均超过3 dB，并且IDPSO-PTS 算法的峰均比抑制能力较改进前的DPSO-PTS 算法提升0.2 dB。综上所述，IDPSO-PTS 算法较DPSO-PTS 和原始UFMC 系统具有更好的峰均比抑制能力。

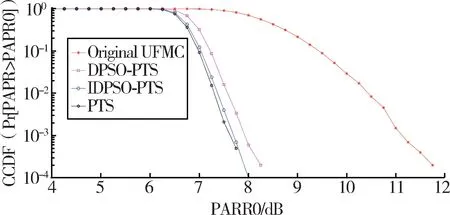
图7 不同算法的PAPR 抑制效果

为验证IDPSO-PTS 算法对误码率的影响，比较了原始UFMC、DPSO-PTS 算法、IDPSO-PTS 算法和PTS 技术的误码率曲线。不同算法对误码率的影响如图8 所示，本文所提IDPSO-PTS 算法与原始UFMC、DPSO-PTS 算法、PTS 技术相比，误码率曲线几乎不发生改变，即采用IDPSO-PTS 算法抑制UFMC 系统的峰均比不会产生额外的误码率。

图8 不同算法的误码率

为验证不同函数分段点α取值对所提IDPSOPTS 算法的影响，分别取α为0.1、0.2、0.3、0.4 时与原始UFMC 进行比较。不同函数分段点取值对IDPSO-PTS 算法的影响如图9 所示，本文所提IDPSO-PTS 算法在函数分段点α取不同值时，峰均比抑制效果略有差异。其中，α取0.2 或0.3 时，IDPSO-PTS 算法所表现出的性能更好。

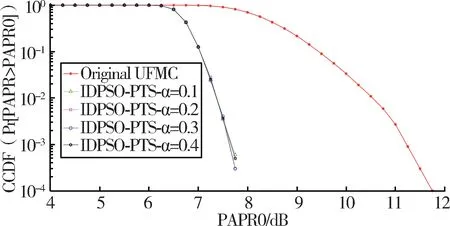
图9 不同函数分段点对IDPSO-PTS 算法的影响

4 结束语

本文提出一种基于改进离散粒子群的IDPSOPTS 算法，并与原始UFMC、DPSO-PTS 算法和传统PTS 技术进行了仿真对比，仿真结果表明：在峰均比抑制效果上，IDPSO-PTS 算法相较于原始UFMC 系统可降低3.5 dB；相较于DPSO-PTS 算法可降低0.2 dB。在计算复杂度上，当候选相位因子组合数目较多时，传统PTS 技术的计算复杂度随着子块数目V的增加呈指数式增长；而IDPSO-PTS 算法的计算复杂度明显低于传统PTS 技术。在误码率性能上，IDPSO-PTS 算法与原始UFMC、DPSO-PTS 算法和PTS 技术相比，误码率曲线几乎完全重合，不产生额外的误码率。综上所述，本文提出的IDPSO-PTS 算法在有效抑制UFMC 系统峰均比的同时，可显著降低计算复杂度，并且不影响误码率性能。