考虑道路负载均衡的码头多AGV无冲突路径规划

温惠英 元昱青 林译峰

考虑道路负载均衡的码头多AGV无冲突路径规划

温惠英 元昱青 林译峰†

（华南理工大学 土木与交通学院，广东 广州 510640）

随着集装箱运输需求的日益增长以及新型信息技术的广泛应用，集装箱码头作业自动化成为国内外港口发展的主要趋势。集装箱码头作业自动化可有效提高码头的作业效率和安全性，降低码头对人力资源的需求和运营成本。水平运输系统是集装箱码头装卸系统的重要组成部分，同时也是实现集装箱在码头前沿与堆场之间运转的重要纽带，其运行的稳定性和调度的合理性将直接影响码头自动化装卸系统的运行效率。自动导引车（AGV）是自动化集装箱码头常用的水平运输设备，承担着从前沿岸桥到后方堆场的集装箱运输任务。在实际作业过程中，多辆AGV同时运作难免会发生冲突和拥堵。基于此，文中采用基于冲突搜索的双层算法（CBS算法）解决码头多AGV协同作业产生的冲突问题，上层算法搜索AGV间的冲突，下层算法采用A*算法对AGV进行路径规划，并在A*算法中引入负载因子，使得规划路径避开拥堵点，实现码头道路的负载均衡。对于码头多任务点连续作业场景下的多车路径规划，基于CBS算法采用一种滑动时间窗冲突解决方法（STWCR）以提升运算效率。通过仿真实验验证了文中所提算法能够有效解决码头多AGV路径规划的冲突问题，同时均衡路网负载，缓解道路局部拥堵现象，提高道路资源的利用率。研究成果为自动化集装箱码头水平运输系统优化提供了参考。

自动化集装箱码头；路径规划；冲突规避；道路负载均衡；A*算法

集装箱码头水平运输作业是连接码头前沿和后方堆场十分关键的一个环节，水平运输作业效率是影响码头作业效率的重要因素。自动化集装箱码头采用自动引导车（AGV）代替传统的人工驾驶车辆，以实现水平运输系统自动化和智能化。对多AGV无冲突路径规划问题进行研究对于提升水平运输的作业效率、保障作业过程的安全可靠、降低车辆行驶的能源消耗等方面都具有重要的意义。

单车路径规划是多车冲突规避的基础，常用的路径规划算法主要有：人工势场法、智能仿生学算法和图形搜索法［1-6］。在已知环境信息的情况下常用图形搜索法进行路径规划，经典的图形搜索法有Dijkstra、A*、Floyd等算法［7-11］。

国内学者对于多AGV路径规划的冲突规避研究多集中在专业制造系统、物流仓储中心等场景，主要的冲突规避解决方法有交通规则法、区域控制法和时间窗法［12-18］。近年来，国外学者将多AGV路径规划问题建模为一个人工智能领域的经典搜索问题，即多Agent路径规划问题（MAPF）［19］。MAPF是指为每个智能体从各自的起始位置到目标位置规划一条相互之间无冲突路径的问题。对MAPF的研究现状进行系统整理和分类，按照规划方式不同，MAPF算法分为分布式规划算法和集中式规划算法。

在分布式规划算法中，每个智能体根据当前获取的环境信息独立执行动作，实时性较强。Guo等［20］设计了一种基于多智能体系统（MAS）的AGV系统体系结构，采用基于黑板模型的改进交互协议作为AGV的通信方法，采用改进Dijkstra算法求解所有AGV的无冲突路径。李静［21］针对自动化集装箱码头多AGV冲突问题，提出一种强化学习的避让控制方法，并通过强化学习的Q学习方法（Q-learning）和深度Q网络（DQN）进行模型的训练，实现AGV实时避让控制。集中式规划算法对所有智能体进行集中规划，规划的速度和效率比分布式规划算法高。Sharon等［22-23］提出了增加代价树搜索算法（ICTS算法）和基于冲突搜索算法（CBS算法）。其中，CBS算法是解决MAPF最热门的方法之一，在大地图场景下展现出了较高的求解效率和较好的求解质量。Ma等［24］针对智能体在到达目的地后立即获得新任务的实时动态系统，提出了一种滚动时域冲突解决方法（RHCR），该方法能够在保证规划质量的同时提升算法运算效率。

目前大多数自动化码头的AGV行驶路径是基于最短路径原则进行规划的，往往会出现多数车集中于最短路径、局部道路负载过大的现象，造成某个路段产生拥堵甚至死锁的问题。基于此。本文采用基于冲突搜索算法（CBS算法）解决多车路径规划中的冲突问题，并针对码头局部道路负载过大引发拥堵的问题，在下层路径规划算法中引入负载因子，避免车辆集中在最短路径上；针对码头多任务点连续作业场景，采用一种滑动时间窗冲突解决方法（STWCR）以提升运算效率，最后进行仿真实验验证与分析。

1　多AGV无冲突路径规划模型

1.1　问题描述

传统二维路径规划算法是对每辆车独立进行路径规划（IPF），而本文的多AGV路径规划则需要协调多辆AGV的路径，让这些AGV能够避免冲突，顺畅地在码头路网中行驶。多AGV协同路径规划的关键是解决节点和路径资源的占用问题。在多AGV运行的路网中，主要产生的冲突类型包括节点冲突、追赶冲突和相向冲突等［25］。

（1）节点冲突

节点冲突是指两辆行驶方向相互垂直的AGV在同一时间经过同一个节点产生的冲突碰撞，如图1所示。

图1　节点冲突示意图

（2）追赶冲突

追赶冲突是指两辆行驶方向相同的AGV行驶于同一路段上，由于后面的AGV的行驶速度大于前面的AGV，即将发生赶超，从而产生的冲突，如图2所示。

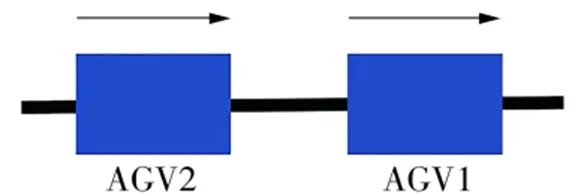
图2　追赶冲突示意图

（3）相向冲突

相向冲突是指两辆方向相反的AGV行驶于同一路段上，在同一时间经过同一个节点产生的冲突碰撞，如图3所示。

图3　相向冲突示意图

1.2　模型假设

基于自动化集装箱码头中AGV的车辆特性，本文针对多AGV路径规划问题提出了如下假设：

（1）AGV的启动加速时间、刹车减速时间以及在转弯过程中所耗费的时间非常短暂，对模型结果的影响可忽略不计。

（2）基于假设（1），可以认为AGV在行驶过程中速度保持恒定，不会发生赶超冲突，因此码头路网主要发生的冲突类型为节点冲突和相向冲突。

（3）本文重点研究多AGV路径规划的冲突规避和道路负载均衡问题，忽略AGV在行驶过程中遇到的随机障碍物的情况。

1.3　模型表示

式（1）表示在任意时刻，有且只有一辆AGV经过路网某一节点，即避免节点冲突；式（2）表示在任意时刻，不允许两辆AGV向彼此的位置移动，即避免相向冲突。

2　考虑码头冲突规避和负载均衡的搜索算法设计

对于多AGV路径规划的冲突规避问题本节采用基于冲突搜索算法（CBS算法）进行求解。该算法由上下两层搜索算法组成，在上层冲突搜索算法中，使用约束树（CT）寻找多个AGV间的冲突，如果存在冲突，则施加相应的约束用于下层路径规划算法中；在下层路径规划算法中，将MAPF分解为多个单AGV，基于上层算法的约束采用单AGV路径规划算法分别为每辆AGV规划路径。由于A*算法具有在搜索最优路径时具有搜索速度快、效率高等优点，本文采用A*算法作为下层路径规划算法。上层算法和下层算法本质都是搜索算法，为了进行区分，上层引入优先级队列OPENcbs，下层引入优先级队列OPEN。

2.1　上层冲突搜索算法

CBS算法的上层搜索是通过约束树来搜索冲突和添加约束，约束树是一种二叉树，树中的任一结点都包含以下3个信息：

（1）.constraints 1个约束集，是由AGV的约束所构成的集合。

（2）.solution 1个解集，是由所有AGV的路径组成的集合。

（3）.cost总成本，是当前结点的解集里所有AGV的路径成本之和。

上层冲突搜索算法的具体步骤如下：

步骤1首先将约束树根节点放入OPENcbs中，此时根节点的约束集.constraints为空，调用下层算法对根节点的所有的AGV进行路径规划生成.solution，计算所有AGV的总路径成本.cost；

步骤2在OPENcbs中取出cost最小的结点作为当前结点，根据式（1）和式（2）对其.solution进行冲突检测。若该结点的解集.solution存在冲突，则进入步骤3；若该结点的解集.solution无冲突，即找到了所有AGV无冲突的路径，输出所有AGV的路径，算法结束；

步骤3从当前结点分支出两个子结点，子结点继承当前结点的约束和解，并针对发生冲突的AGV分别添加新的约束以避免冲突；

步骤4根据约束集.constraints生成子结点的解.solution，这里只需对有添加新约束的AGV调用下层算法进行路径规划，约束没有发生改变的AGV可以将路径直接从父结点保留下来。

步骤5根据子结点的解.solution计算子结点的.cost。

步骤6把分支出来的所有子结点放入OPENcbs中，当OPENcbs不为空时，重复步骤2。

2.2　下层路径规划算法

下层路径规划采用A*算法对所有AGV进行最优路径搜索，因此往往会出现多数车辆都集中在码头路网中的同一路径上使得码头道路利用率不均衡的现象，并产生了交通拥堵。为了使路网中各路径上的AGV数量达到实时动态平衡，本文在A*算法的启发式函数中引入负载因子来衡量道路的拥堵状态，当道路负载达到一定程度时，AGV需绕开此路进行重新规划。改进后的A*算法的启发式函数（）表示如下：

下层路径规划的改进A*算法具体步骤如下。

步骤1首先将起点v放入OPEN中，设v的父节点为空。

步骤2在OPEN集合中选择引入负载因子的（）值最小的节点作为当前节点，若该节点是目标节点，即找到了该AGV从起点到终点的最优路径，算法结束；若该节点不是目标节点，则进入步骤3。

步骤3找到所有与当前节点相邻的节点进行扩展，若相邻节点不在OPEN里，那么把该节点放入OPEN中，并设置该节点的父节点为当前节点；若相邻节点已在OPEN里，那么重新计算该节点的（）值，如果重新计算的（）值小于原（）值，则更新OPEN里该节点的（）值并设该节点的父节点为当前节点。

步骤4当OPEN集合不为空时，重复步骤2，否则未找到路径，算法结束。

通过在A*算法中引入负载因子可以自动调控路网车流量，把较为繁忙路段的车流量调节至较为空闲的路段，从而实现道路负载均衡。

2.3　多任务点连续作业

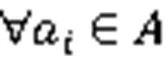
STWCR算法的具体步骤如下：

步骤1首先获取所有AGV的起点和第一个目标位置点作为当前规划的起始位置和目标位置；

步骤2采用改进A*算法对所有AGV从起始位置到目标位置进行路径规划，调用CBS算法只解决时间窗值内的路径冲突；

步骤3获取最先到达目标位置的AGV到达的时刻，把时刻下的所有车所处的当前位置作为新一轮规划中起始位置；

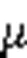
步骤5重复步骤2，直到当所有的AGV都到达各自的最后一个目标位置点时，算法结束。

算法流程图如图4所示。

图4　STWCR算法流程图

STWCR算法示意图如图5所示。与传统的lifelong-MAPF求解器不同，STWCR用改进A*算法对所有车进行路径规划，但并不是解决所有路径的冲突，而是调用CBS算法只解决时间窗值内的冲突［24］。这样可以有效地减少算法在搜索时扩展的不必要节点数量，节省了计算空间，提高运算效率。这里需要注意的是，以保证所有车从起点到最后一个目标位置的路径都是无冲突路径。该方法既可以解决多任务点连续作业的lifelong-MAPF问题，同时可以提升算法运行效率。

图5　STWCR算法示意图

3　仿真实验分析

本文以广州南沙港四期自动化集装箱码头布局为参考，研究码头多AGV的无冲突路径规划，码头布局如图6所示。

图6　码头布局图

由于码头路网的堆场面积较大且布局规整，AGV行走方向为竖直方向和水平方向，因此，本文选取栅格地图法来进行环境地图的构建。根据实际的码头平面布局，构建40×20的局部码头作业环境栅格图，如图7所示。以栅格中心点为坐标点，每个栅格大小相同且具有各自的位置坐标（，），从当前栅格到达相邻栅格需要耗费1个时间步。用所有AGV规划路径的时间步总数来计算路径总成本，路径总成本用参数来表示，单位为时间步。

图7　码头作业环境栅格地图

码头前沿中AGV和岸桥进行交接集装箱的位置为岸桥作业点，分别为1-4；堆场箱区旁的作业车道中AGV和场桥进行交接集装箱的位置为场桥作业点，分别为1-54。岸桥作业点和场桥作业点对应的位置坐标如表1、表2所示。

表1　岸桥作业点位置坐标

表2　场桥作业点位置坐标（节选）

为了分析算法的性能，设计了不同规模的问题进行求解。在码头前沿设置4台岸桥，对应4个岸桥作业点，堆场设置9个箱区，每个箱区对应6个场桥作业点，一共54个场桥作业点，水平运输设备配置AGV18辆。对每辆AGV随机生成作业任务，每个作业任务的起点和终点对应岸桥作业点或场桥作业点，将作业任务对应的作业点转化成位置坐标，作为多车路径规划算法的输入。AGV在作业点停留的时间设为固定值。所有的仿真实验在CPU为I9-12900KF，内存为16 GB的电脑上运行，用Python语言实现。

3.1　多AGV冲突避免仿真实验

本节分别设置两辆相向行驶的AGV和两辆垂直行驶的AGV进行实验以验证CBS算法解决相向冲突和节点冲突的有效性。如图8、图9所示，相向冲突方面，图8（a）为未使用算法的时空三维图，图8（b）为使用算法的时空三维图；节点冲突方面，图9（a）为未使用算法的时空三维图，图9（b）为使用算法的时空三维图，时空三维图的轴和轴为空间维度，轴为时间维度。

图8　相向冲突下时空三维图对比

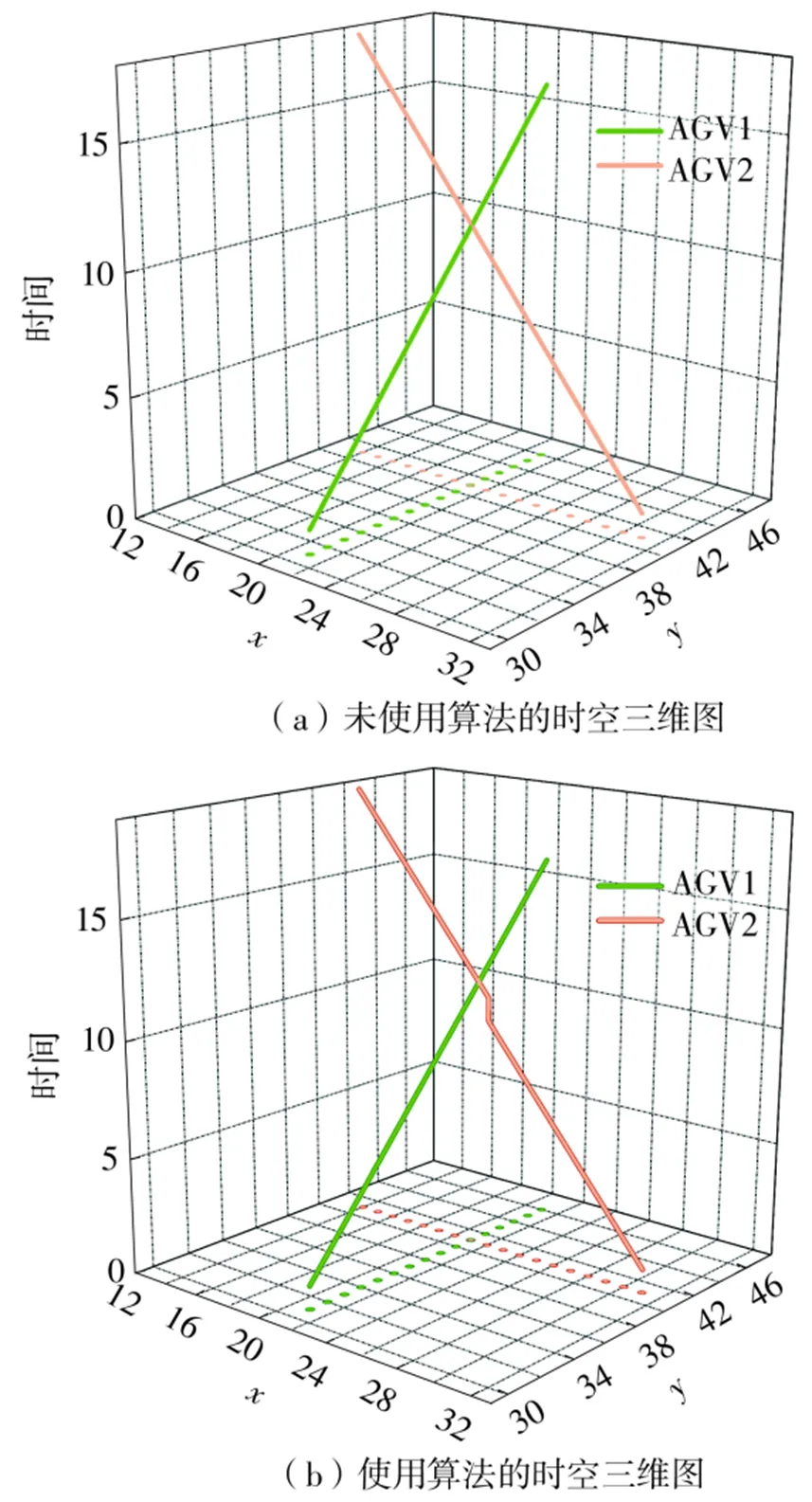
图9　节点冲突下时空三维图对比

从图8（a）、图8（b）可看出，未使用CBS算法进行路径规划时，两车相向行驶，在=11时在坐标（19，41）处发生冲突；使用CBS算法进行路径规划时，上层算法检测到了冲突｛1，2，（19，41），11｝，对AGV1施加约束｛1，（19，41），11｝，下层算法基于约束为AGV1重新规划最短路径，AGV1从（19，40）到（20，40），避开了（19，41），从而避免了两车在行驶过程中的冲突。从图9（a）、图9（b）可看出，未使用CBS算法进行路径规划时，两车朝着各自的目标位置行驶，当=11时在坐标（21，41）处两车会产生冲突；使用CBS算法进行路径规划时，上层算法检测到了冲突｛1，2，（21，41），11｝，对AGV2施加约束｛2，（21，41），11｝，AGV2在（22，41）停留了一个时间步长从而避免了冲突。由此可见，CBS算法可以有效解决多AGV路径规划中存在的相向冲突和节点冲突。

为进一步验证CBS算法在多AGV路径规划中解决多种冲突并存的有效性，设置不同数量的AGV执行点对点运输任务，分别采用IPF和CBS算法对AGV进行路径规划。记录每个算例下的所有AGV的路径总成本和发生冲突的总次数，算法使用前后对比如表3所示。

通过表3可得，在10组车辆数不同的算例中，CBS算法的路径总成本要稍高于IPF，这是因为在CBS算法的规划下，多车为避免冲突会停车等待或者重新规划路径从而使变长，但的偏差在0.25%～0.82%范围内，说明CBS算法对最终路径规划结果的最优性影响不大。根据统计每个算例下发生冲突的总次数可得，采用IPF对多车进行路径规划，车辆间存在冲突，且随着车数辆越多冲突越明显，而CBS算法规划的路径不存在车辆间的冲突。综上所述，当路网中AGV数量较多且多种冲突并存时，CBS算法在对路径规划结果的最优性影响不大的情况下，可以有效解决多车路径规划的冲突问题，实现车辆间的冲突规避。

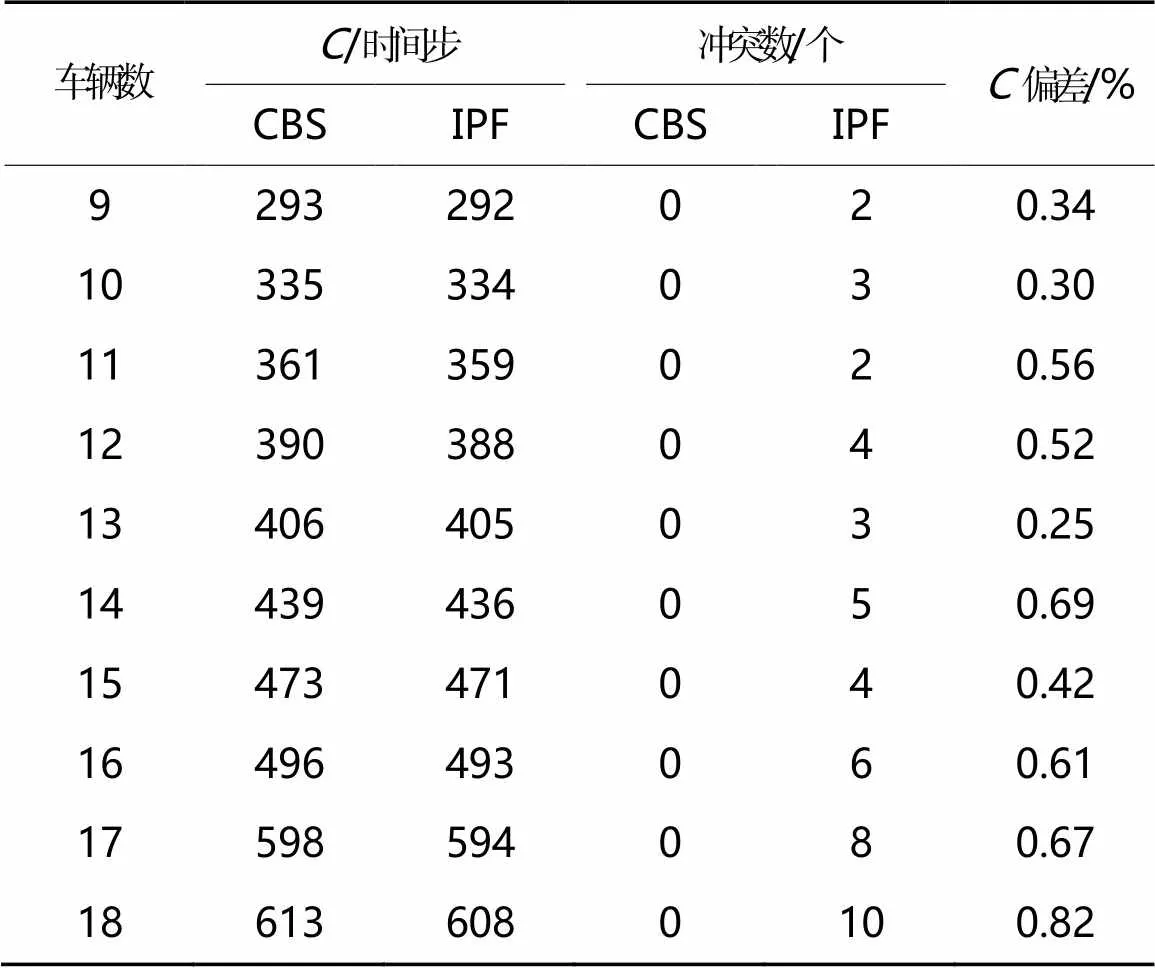
表3　算法使用前后对比

3.2　多任务点连续作业仿真实验

本节设计实验对STWCR算法在解决多任务点连续作业场景下的多车路径规划问题的算法性能进行分析。设置不同数量的AGV执行多个水平运输作业任务，分别用传统lifelong-MAPF求解器（算法1）和STWCR算法（算法2）进行求解。采用路径总成本、算法运行时间和算法扩展节点数作为算法的评价指标对算法性能进行分析。

两种算法的值对比如表4所示。由表可知，由于在该场景下，AGV需要连续执行多个任务，因此STWCR求解的均多于表3中CBS求解的，规划的路径也会更加复杂。从路径总成本来看，两种算法规划的路径总成本偏差均在0.55%以内，说明STWCR的路径规划最优性不变，仍是最短路径规划。

表4　2种算法的C结果对比

两种算法扩展节点数和算法运行时间对比结果如图10所示，从算法扩展节点数来看，在所有算例中，STWCR均能有效地减少算法在搜索时扩展的不必要节点数量，节省了计算空间，优化率在8.2%到20.51%之间；从算法运行时间来看，STWCR均能有效地降低算法运行时间，提高运算效率，且随着问题规模的增大，STWCR的优势愈发明显。在所有算例中，STWCR算法对算法运行时间的平均优化率达18.98%，进一步验证了STWCR算法在提高运算效率上的优越性。

图10　两种算法扩展节点数和运行时间对比

3.3　多AGV路径规划负载均衡仿真实验

为了分析多任务点连续作业场景下多车路径规划的道路负载情况，本节对STWCR每轮规划中的下层路径规划采用引入负载因子的改进A*算法进行仿真实验。算例的生成与上一节相同，实验1采用STWCR，实验2在STWCR中引入负载因子，分别对不同AGV数量下的路径规划算例进行求解。统计路网内经过所有可行节点的规划路径条数作为这些节点的负载，对所有可行节点的负载量从高到低进行排序，取前15个高负载节点的负载量，计算它们的标准差和均值，以此作为实验指标分析路网负载情况。

实验对比结果如表5所示。由表可知，随着车辆数以及任务数的增多，规划路径的总成本增加，在所有算例中，实验2的有部分比实验1稍高，但两者的偏差量在0.28%以内。这是因为引入了负载因子后，使得某些AGV在规划路径时可能会避开较为拥堵的最短路径，从而导致规划路径的总成本增加，由于两者的偏差量十分微小，其对最终整体路径规划结果的影响可以忽略不计。

表5　引入负载因子前后C值对比

不同AGV数量下的路网节点负载情况如图11所示。由图可知，在车辆数不同的所有算例中，实验2的整体道路负载量相较于实验1有所降低，说明了实验2把实验1中负载较大的区域的车流量均衡分流到了其他区域，从而避免了局部车流量过大，算法呈现了一定的道路负载均衡作用。

图11　路网节点负载对比

不同AGV数量下的路网高负载节点的均值和方差如图12所示。从平均负载来看，实验2中所有算例的平均负载均比实验1有所降低，平均降低幅度为5.23%；从标准差来看，实验2的道路负载量标准差相较于实验1也有一定程度地降低，说明引入负载因子后算法能够有效降低高负载节点的负载量，避免产生局部车流量过大导致拥堵，并能够较好地均衡道路负载，提高码头道路的利用率。

图12　路网高负载节点的均值和方差对比

4　结语

本文针对多AGV协同作业产生的冲突问题提出基于冲突搜索的两层搜索算法，并在下层路径规划算法中引入负载因子对A*算法进行优化，以解决多车最短路径规划中道路负载不均衡引发的局部拥堵问题，对于码头多任务连续作业场景下的life-long MAPF问题，采用STWCR算法进行求解以提升运算效率。实验结果表明，本文所提出的算法可以有效解决码头多车路径规划中的冲突问题，并且能够减少算法在搜索时扩展的不必要节点数量，算法运行时间降低18.98%，下层算法引入负载因子后，算法平均负载降低了5.23%。研究结果表明，本文所提算法在解决多车冲突的基础上可以有效均衡道路负载，缓解局部拥堵。研究成果对于码头的实际生产和运营有着重要的指导作用。

本文重点分析了码头中多AGV路径规划，但对于自动化集装箱码头中的任务分配，即分配集装箱装卸任务给指定的AGV来执行这个过程没有涉及，对于整个自动化集装箱码头的水平运输系统来说，AGV任务调度与路径规划的协同优化问题还需要进一步研究。此外，本文研究的路径规划对很多实际情况进行了抽象化，忽略了AGV在实际运输过程中的很多不确定性因素，如任务需求的变动、作业设备突发故障、AGV的电量情况等等，下一步的研究工作可以把这些因素也考虑进算法之中。

［1］XIE S T，HU J Y，BHOWMICK P，et al．Distributed motion planning for safe autonomous vehicle overtaking via artificial potential field［J］．IEEE Transactions on Intelligent Transportation Systems，2022，23（11）：21531-21547.

［2］HUANG Y，DING H，ZHANG Y，et al．A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach［J］．IEEE Transactions on Industrial Electronics，2019，67（2）：1376-1386.

［3］AZZABI A，NOURI K．An advanced potential field method proposed for mobile robot path planning［J］．Transactions of the Institute of Measurement and Control，2019，41（11）：3132-3144.

［4］LIYUN X，NING W，XUFENG L．Study on conflict-free AGVs path planning strategy for workshop material distribution systems［J］．Procedia CIRP，2021，104：1071-1076.

［5］ZHONG M，YANG Y，DESSOUKY Y，et al．Multi-AGV scheduling for conflict-free path planning in automated container terminals［J］．Computers & Industrial Engineering，2020，142：106371.

［6］ZHOU Y，HUANG N．Airport AGV path optimization model based on ant colony algorithm to optimize Dijkstra algorithm in urban systems［J］．Sustainable Computing：Informatics and Systems，2022，35：100716.

［7］许伦辉，曹宇超，林培群．基于多影响因素RDMA～*算法的无人驾驶动态路径规划［J］．交通信息与安全，2020，38（2）：24-36.

XU Lunhui，CAO Yuchao，LIN Peiqun. Dynamic path planning for unmanned driving based on multi-influencing factors RDMA* algorithm［J］．Journal of Transport Information and Safety，2020，38（2）：24-36.

［8］WU M P，GAO J，LI L，et al．Control optimisation of automated guided vehicles in container terminal based on Petri network and dynamic path planning［J］．Computers & Electrical Engineering，2022，104：108471.

［9］YUE L，FAN H．Dynamic scheduling and path planning of automated guided vehicles in automatic container terminal［J］．IEEE/CAA Journal of Automatica Sinica，2022，9（11）：2005-2019.

［10］左秀峰，沈万杰．基于Floyd算法的多重最短路问题的改进算法［J］．计算机科学，2017，44（5）：232-234，267.

ZUO Xiufeng，SHEN Wanjie．Improved algorithm about muti-shortest path problem based on floyd algorithm［J］．Computer Science，2017，44（5）：232-234，267.

［11］SINGGIH I K，HONG S，KIM K H．Flow path design for automated transport systems in container terminals considering traffic congestion ［J］．Industrial Engineering & Management Systems，2016，15（1）：19-31.

［12］MARTIN J，CASQUERO O，FORTES B，et al．A generic multi-layer architecture based on ROS-JADE integration for autonomous transport vehicles［J］．Sensors，2018，19（1）：69.

［13］高一鹭，胡志华．基于时空网络的自动化集装箱码头自动化导引车路径规划［J］．计算机应用，2020，40（7）：2155-2163.

GAO Yilu，HU Zhihua．Path planning for automated guided vehicles based on tempo-spatial network at automated container terminal［J］．Journal of Computer Applications，2020，40（7）：2155-2163.

［14］LI Q，POGROMSKY A，ADRIAANSEN T，et al．A control of collision and deadlock avoidance for automated guided vehicles with a fault-tolerance capability［J］．International Journal of Advanced Robotic Systems，2016，13（2）：64.

［15］张素云，杨勇生，梁承姬，等．自动化码头多AGV路径冲突的优化控制研究［J］．交通运输系统工程与信息，2017，17（2）：83-89.

ZHANG Suyun，YANG Yongsheng，LIANG Chengji，et al．Optimal control of multiple AGV path conflict in automated terminals［J］．Journal of Transportation Systems Engineering and Information Technology，2017，17（2）：83-89.

［16］张中伟，张博晖，代争争，等．基于动态优先级策略的多AGV无冲突路径规划［J］．计算机应用研究，2021，38（7）：2108-2111.

ZHANG Zhongwei，ZHANG Bohui，DAI Zhengzheng， et al. RMulti-AGV conflict-free path planning based on dynamic priority strategy ［J］. Application Research of Computers，2021，38（7）：2108-2111.

［17］LIANG C，ZHANG Y，DONG L. A three stage optimal scheduling algorithm for AGV route planning considering collision avoidance under speed control strategy［J］．Mathematics，2022，11（1）：138.

［18］SMOLIC-ROCAK N，BOGDAN S，KOVACIC Z，et al．Time windows based dynamic routing in multi-AGV systems［J］．IEEE Transactions on Automation Science and Engineering，2010，7（1）：151-155.

［19］万千．基于CBS算法的物流分拣多AGV路径规划的研究［D］．哈尔滨：哈尔滨工业大学，2018.

［20］GUO K，ZHU J，SHEN L．An improved acceleration method based on multi-agent system for AGVs conflict-free path planning in automated terminals［J］．IEEE Access，2020，9：3326-3338

［21］李静．基于在线学习的自动化码头AGV调度方法研究［D］．大连：大连理工大学，2018.

［22］SHARON G，STERN R，GOLDENBERG M，et al．The increasing cost tree search for optimal multi-agent pathfinding［J］．Artificial Intelligence，2013，195：470-495.

［23］SHARON G，STERN R，FELNER A，et al．Conflict-based search for optimal multi-agent pathfinding［J］．Artificial Intelligence，2015，219：40-66.

［24］MA H，LI J Y，KUMAR T K S，et al．Lifelong multi-agent path finding for online pickup and delivery tasks ［C］∥Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems （AAMAS）．Sao Paulo：ACM，2017：837-845

［25］HU Y，YANG H，HUANG Y．Conflict-free scheduling of large-scale multi-load AGVs in material transportation network［J］．Transportation Research Part E：Logistics and Transportation Review，2022，158：102623.

［26］刘恒麟．多AGV路径规划算法的研究与实现［D］．南京：东南大学，2020.

Conflict-Free Path Planning For Multi-AGVs in Automated Terminals Considering Road Load Balancing

（South China University of Technology，School of Civil Engineering & Transportation，Guangzhou 510640，Guangdong，China）

With the increasing demand for container transportation and the widespread application of new information technologies, the automation of container terminal operations has become the main development trend in domestic and international ports. It can not only effectively improve the efficiency and safety of terminal operations, but also significantly reduce the demand for human resources and the operational costs. The horizontal transportation system is an essential part of the container terminal handling system and an important link enabling the highly efficient container transportation between the quayside and the storage yard, so its operational reliability and the reasonableness of the scheduling directly affect the operational efficiency of the automated container handling system. The mostly used horizontal transportation equipment in container terminals is the automated guided vehicles (AGVs), which is responsible for horizontal transportation from the front quay crane to the rear yard in automated container terminals. In actual operation process, conflicts and congestion is inevitable when multiple AGVs operate simultaneously. On this basis, this paper used conflict-based search (CBS) to solve the conflict problem arising from the cooperative operation of multi-AGVs at the terminal. The upper layer algorithm searched for conflicts among AGVs, while the lower layer algorithm used the A* algorithm for path planning of AGVs. A load factor was introduced into the heuristic function of the A* algorithm in order to avoid congestion in the path planning and achieve load balancing on terminal roads. Further, a sliding time window conflict resolution (STWCR) based on CBS was adopted to improve computational efficiency for multiple AGVs path planning in the continuous operation scenario of multiple task points at the terminal. Simulation experiments verified that the proposed algorithm in this paper can effectively solve the conflict problem of multiple AGVs path planning at the terminal, while balancing the road network load, alleviating local road congestion, and improving the utilization of road resources. The research results of this paper provide a reference for the optimization of the horizontal transportation system in automated container terminals.

automated container terminal；path planning；conflict avoidance；road load balancing；A* algorithm

Supported by the Natural Science Foundation of Guangdong Province （2023A1515011322）

10.12141/j.issn.1000-565X.230227

2023⁃04⁃11

广东省自然科学基金资助项目（2023A1515011322）

温惠英（1965-），女，博士，教授，主要从事交通安全、物流规划与管理研究。E-mail： hywen@scut.edu.cn

U691

1000-565X（2023）10-0001-10