低渗煤中N2吸附模型适用性分析
2023-11-09杨靖浩刘会虎徐宏杰
杨靖浩,刘会虎*,张 琨,薛 生,徐宏杰
(1.安徽理工大学地球与环境学院 安徽淮南 232001;2.合肥综合性国家科学中心能源研究院(安徽省能源实验室) 安徽合肥 230031)
0 引言
注气开采煤层气是低渗煤层气田重要的增产技术。对于透气性差、渗透率低的煤层,传统的负压抽采耗时长、收效慢,不能满足抽采和井下安全生产的需要[1-3]。向煤层注入气体不仅提高了煤体内部压力和瓦斯渗流速度,而且降低了有效瓦斯分压,促进了吸附气体的解吸[4-5]。
前人对注氮促进瓦斯排放/抽气过程建立了各种吸附模型,发现在不同的实验条件下,N2在煤储层中的吸附过程符合不同的吸附模型。高江涛等采用美国康塔公司的AutosorbIQ-C 型全自动吸附仪研究了CH4/N2/CO2在阜生煤矿煤样表面吸附特性,得到煤样对CH4、N2和CO2吸附的等温吸附曲线[6]。李斌以无烟煤、焦煤和长焰煤为研究对象,开展应力状态下不同煤阶煤的CO2、CH4和N2吸附-形变-渗流实验研究,揭示了不同煤阶煤的吸附、扩散、渗流、形变及气体竞争吸附的特征规律和机理[7]。于洪观利用SPSS 软件对Langmuir、Freundlich、Langmuir-Freundlich、Toth、扩 展Langmuir、BET、D-R、D-A 等8 个模型以及3 个曲线回归方程对晋城和潞安二煤CH4吸附实验数据进行拟合,并分别检验了实验数据的拟合程度[8];赵天逸等分别归纳总结了Herry 吸附式、Freundlich 经验公式、Langmuir 模型、扩展的Langmuir 模型等6 种单组分等温吸附模型以及负载比关联式、理想吸附溶液等4种多组分等温吸附模型[9]。
以前的学者在进行等温吸附试验时,多使用高渗透性煤样,对于低渗煤样吸附研究较少。本文以刘庄矿13 煤与祁东矿7 煤为试验对象,研究低渗煤N2吸附模型的适用性,选用了Langmuir 模型(简称L模型)、Toth 模型(简称T 模型)、Dubinin-Astakhov(简称D-A 模型)、Dubinin-Radushkevich 模型(简称D-R 模型)、Optimize Langmuir 模型(简称优化L 模型)、Optimize Toth 模型(简称优化T 模型)、Optimize Dubinin-Astakhov 模型(简称优化D-A 模型)、Optimize Dubinin-Radushkevich 模型(简称优化D-R模型),共8种吸附模型对低渗煤中N2吸附试验数据的适用性进行分析,以期为低渗煤中N2吸附机理特征分析及瓦斯资源评价提供地质依据。
1 试验材料与方法
1.1 研究区概况
选择两组不同地区的煤样进行等温吸附试验,分别为安徽省阜阳市颍上县境内刘庄矿13 煤和安徽省宿州市埇桥区祁县镇的祁东矿7 煤,采样区位置如图1 所示。选定煤层的基本物性结果如表1 所示。从矿井掘进面、工作面采集来具有代表性的原始煤样,按照国家标准规定(GB/T474—2008)[10],对样品进行反复的破碎、粉碎、筛分等操作步骤,制取粒度为40~60目的煤样200g。

表1 煤的基本物性测试结果Table 1 Basic physical property test results of coal
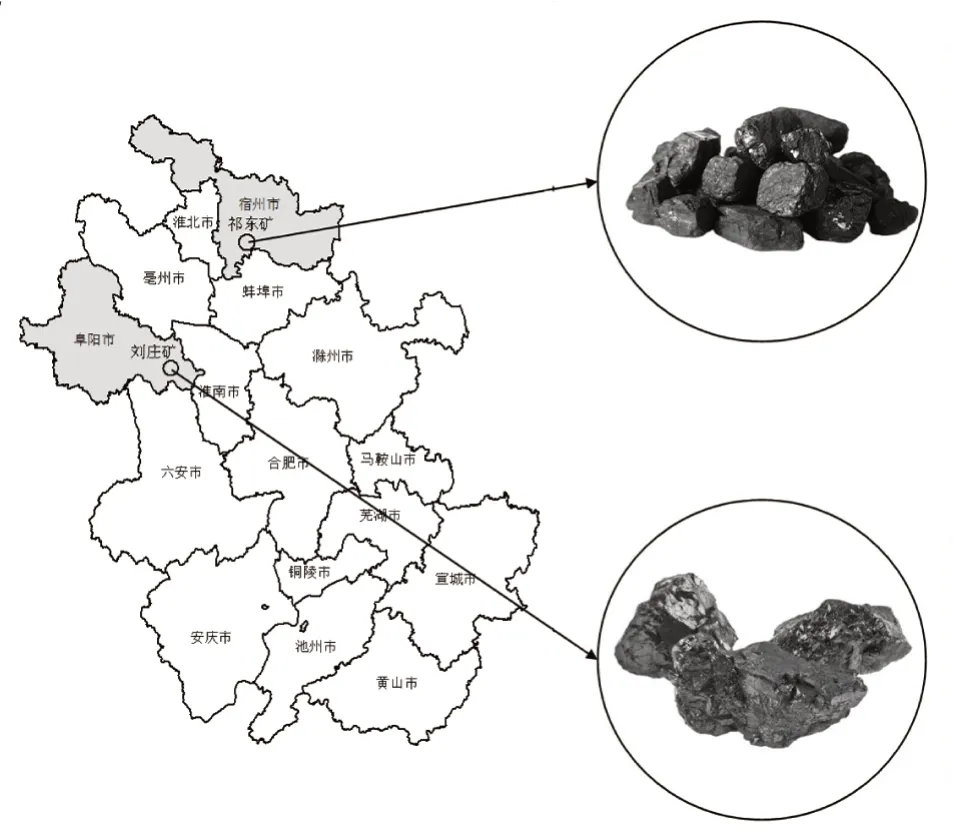
图1 采样区位置Figure 1 Location of sampling areas
1.2 试验条件与试验流程
1.2.1 试验条件
以地层埋深900m 时地质条件作为试验条件,向装置注入N2,设置试验温度为36℃,注入压力分别为0.5、1、2、3、5、6、9MPa。
1.2.2 试验流程
试验依照(GB/T19560—2008)[11]进行:①煤样进行平衡水处理;②准确称量所需试验煤样,装入样品罐;③调节水浴温度,使样品罐和参考罐的温度稳定在36℃,注入氦气,测试系统气密性;④向系统充入氦气,计算样品罐内自由空间体积;⑤抽试验系统及管道真空,注入N2达到试验压力;⑥数据采集;⑦根据参考罐、样品罐的平衡压力及温度,计算不同平衡压力点的吸附量;⑧改变样品,重复试验步骤①至步骤⑦的操作。
1.3 试验系统
试验采用自制的吸附试验装置,可以模拟不同温度、不同气体下的等温吸附实验。装置由以下几个装置组成:①气源模块装置:防爆气瓶柜、高压气瓶、气体浓度检测仪、高压气体调压阀、气体单向阀、供气管路;②气体增压模块装置:气体增压泵、空气压缩机;③信息采集与控制模块装置:压力传感器、温度传感器、数据采集模块、计算机及相关配件、配套仪器温度控制和信息采集软件;④吸附模块:恒温水浴箱、气体罐、水浴箱升降控制系统等组成;⑤抽真空模块:真空泵、负压表等组成(图2)。
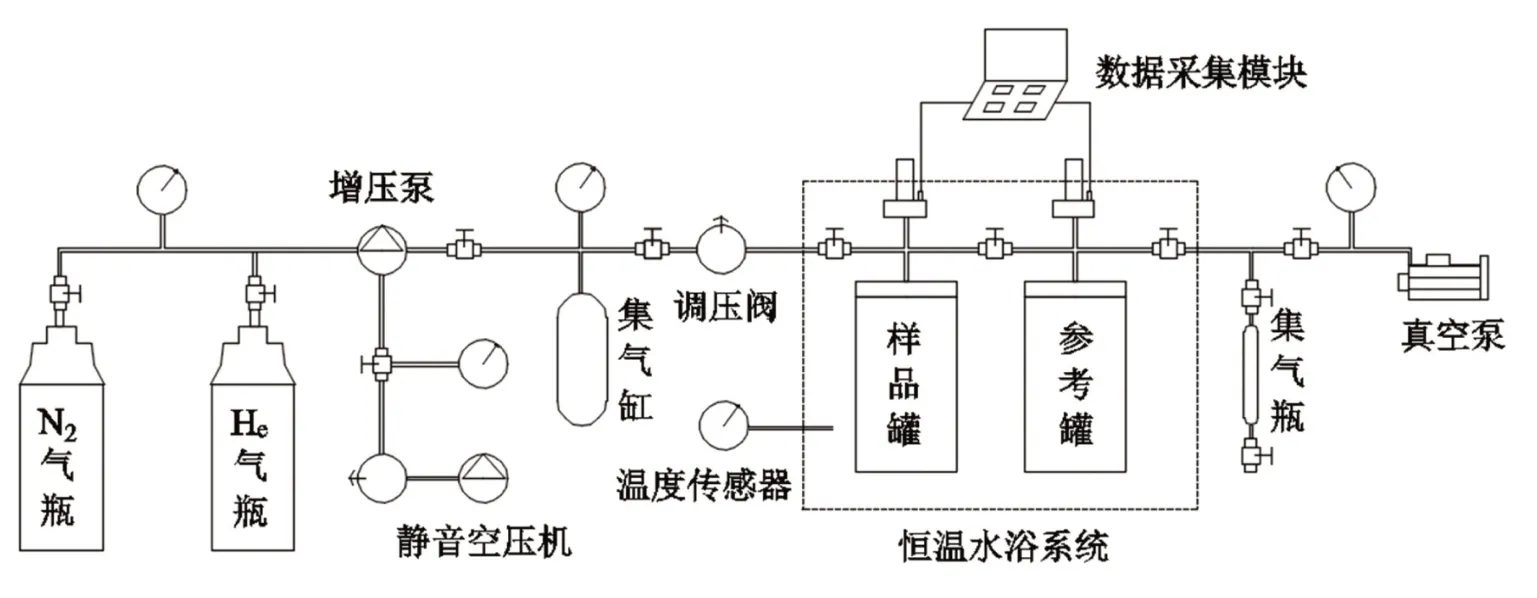
图2 试验系统Figure 2 Test system
1.4 试验方法
使用 1stOpt15pro 软件基于麦夸特法(Levenberg-Marquardt)将试验数据与吸附模型进行拟合,得出各模型的参数与计算值。麦夸特法采用标准-通用全局优化模式,对吸附模型参数具有良好的拟合效果。该算法设定收敛判定指标为1.00×10-10,最大迭代数为1 000,每个参数需要进行30 次以上的计算,直到两个拟合参数值之差在规定范围内,保证参数均大于0,拟合回归系数平方R2大于0.900。
通过对回归系数平方R2、标准差s和相对误差v的综合分析,选出最优的低渗煤层N2吸附模型。
2 吸附模型
对吸附模型的分析不仅可以为过剩吸附量与吸附条件之间的关系找到一个方便的数学表达式,而且可以了解吸附的微观机理。本文使用两类典型的吸附模型及其优化模型,这些模型的参数均具有物理意义。
2.1 第一类吸附模型
基于吸附动力学,包括L 模型、T 模型及其优化模型,这些模型的基本假设是吸附热恒定,吸附剂表面均匀,被吸附的分子之间没有相互作用,分子吸附主要是单层吸附[12]。
L模型:
T模型:
优化L模型:
优化T模型:
式中:V为吸附量,cm3/g;VL是朗缪尔体积,cm3/g;p为吸附平衡压力,MPa;pL为单位质量煤达到朗缪尔体积的一半时所对应的朗缪尔压力,MPa;Kb与n为Toth 常数;ρg为自由相密度,g/m3;ρa为吸附相密度,g/m3。
2.2 第二类吸附模型
以吸附势能理论为基础,包括D-R 模型、D-A模型及其优化模型。吸附势能理论是Dubinin 微孔填充理论的基础,是描述微孔吸附剂,特别是碳质微孔吸附剂气相吸附行为的最成熟、最实用的理论体系[13]。
D-A模型:
D-R模型:
优化D-A模型:
优化D-R模型:
式中:V0为孔隙体积,cm3/g;D为与净吸附热有关的常数;n为温度与孔径分布有关的无量纲常数;p0为饱和蒸汽压,MPa,可通过(Antoine)公式计算:
式中:p0为物质的饱和蒸气压,毫米汞柱;t为温度,℃;A、B、C为无量纲常数[14]。
3 试验结果与讨论
3.1 试验气体吸附特征
表2 为36℃(309.15K)时压力平衡点处的试验吸附量,图3 为36℃(309.15K)等温吸附曲线。如表2 所示,QD 样品N2饱和吸附量是LZ 样品的1.01~1.14倍,QD样品对N2的吸附能力要高于LZ样品,这与前人得出的煤阶(Ro,max<4.0%)越高吸附能力越强的理论相符合[15]。如图3 所示:①两组煤样N2吸附呈现类似吸附特征,符合经典IUPAC 等温吸附分类标准中的第Ⅰ型等温吸附曲线,在2MPa 左右出现拐点;②N2吸附主要包括两个阶段:在0~2MPa 的低压力阶段,吸附量急剧上升;在2~9MPa 高压力阶段,吸附量趋于平缓;③QD与LZ样品等温吸附线在拐点(2MPa)之前,吸附量大致重合,在拐点之后,QD样品对N2的吸附量高于LZ样品。

表2 36℃(309.15K)试验吸附量Table 2 Test adsorption capacity at 36°C(309.15K)cm3/g
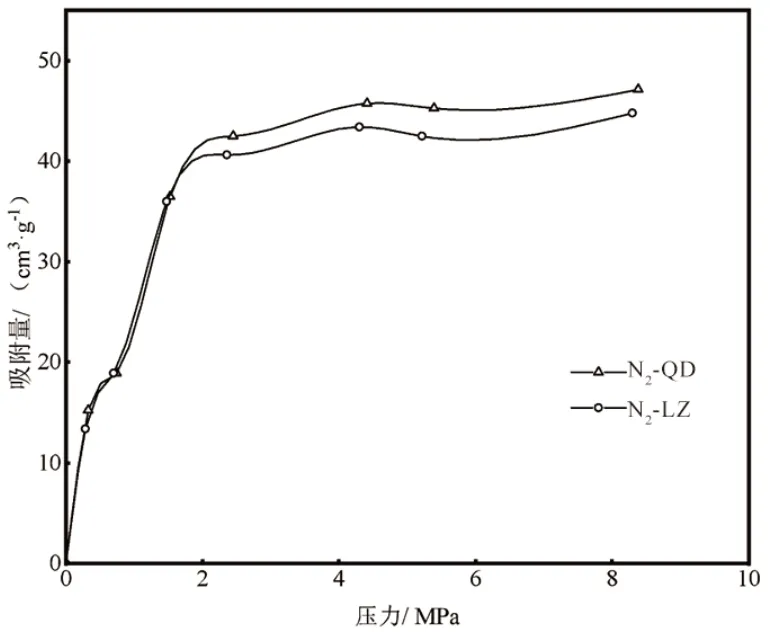
图3 36℃(309.15K)吸附等温曲线Figure 3 Adsorption isotherms at 36°C(309.15K)
3.2 吸附模型的拟合与比较
以QD 煤样为例,分析N2对不同吸附模型的拟合效果。表3 为36℃(309.15K)下等温吸附模型拟合参数,图4 为36℃(309.15K)下不同吸附模型拟合出的等温吸附曲线。如图4 所示,不同吸附模型拟合后的曲线具有不同的形态,D-R 模型拟合后的曲线与试验数据重合度较差,其余7 种模型的曲线形态相似,具有很高的重合度。
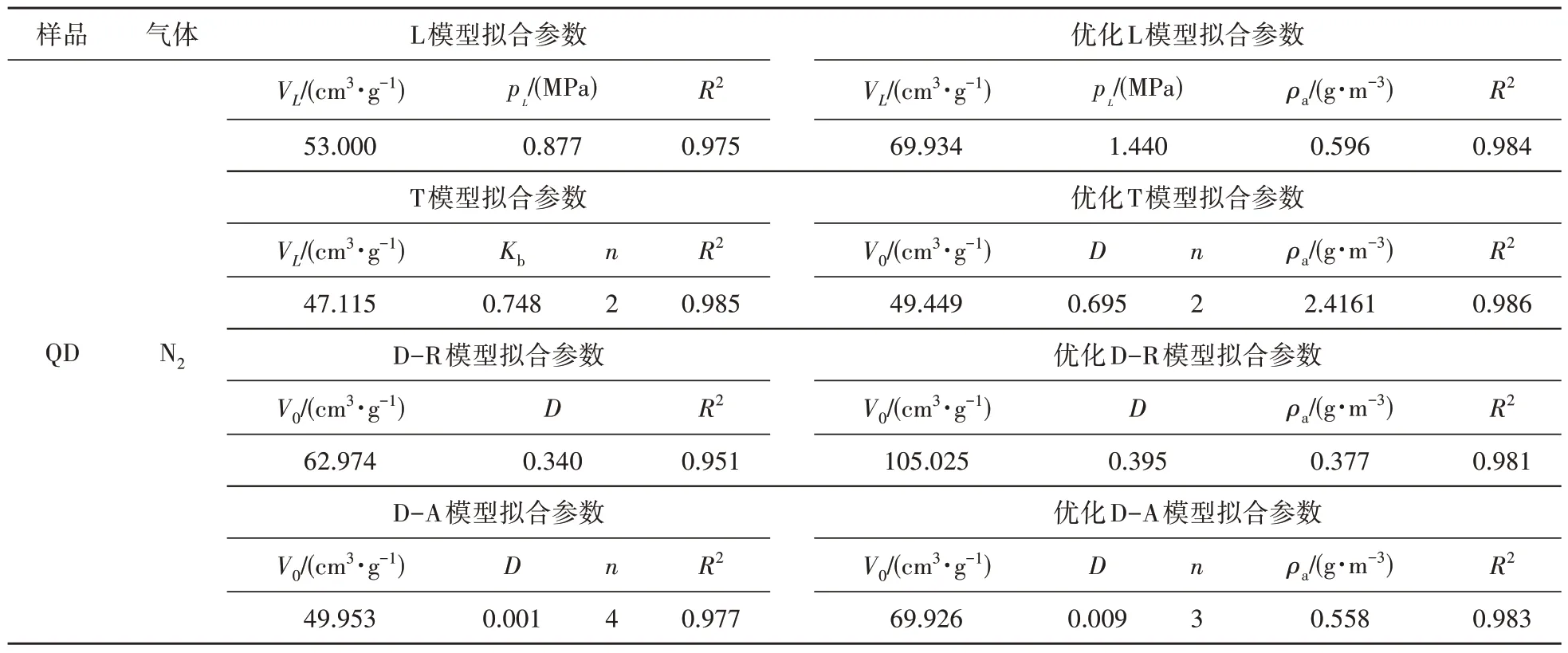
表3 36℃(309.15K)下等温吸附模型拟合参数Table 3 Isothermal adsorption models fitting parameter table at 36°C(309.15K)
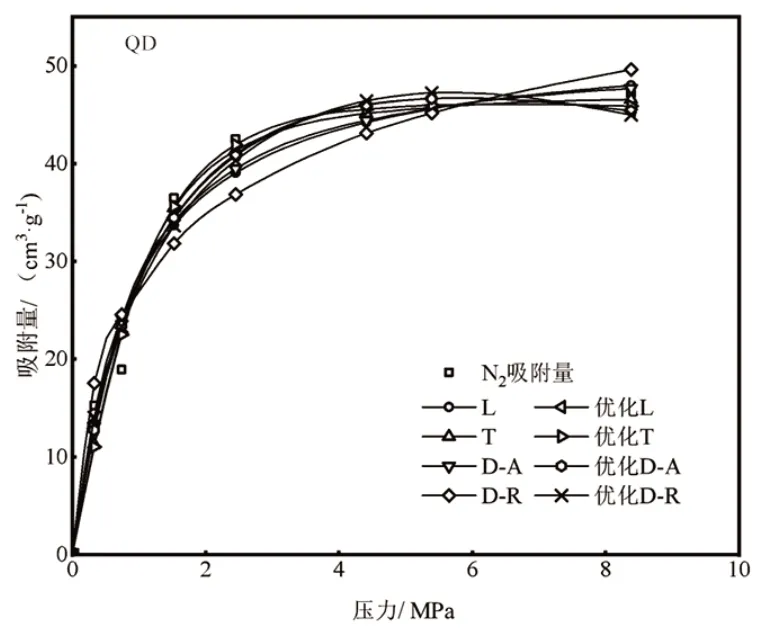
图4 36℃(309.15K)下不同吸附模型等温吸附曲线Figure 4 Isothermal adsorption curves for different adsorption models at 36°C(309.15K)
对表3 的模型拟合参数进行分析,为使模型具有物理意义,实验所得模型参数应具备以下条件:①参数必须具有物理意义;②模拟结果必须符合深部煤层的吸附特征。基于以上的标准,在比较吸附模型时,回归的模型参数VL、PL、V0、n、D、Kb和ρa必须为正值,参数n必须是非零正整数[16]。
由表3 可得,模型拟合计算得到的回归系数R2均在0.900 以上,优化L、T、优化T、优化D-A 和优化D-R 模型的适用性比较好,R2在0.980 以上;其次是L、D-A 和D-R 模型,R2在0.950 以上。在不同吸附模型中,吸附能力的含义存在差异,模型的吸附能力由第一类吸附模型中的朗缪尔体积VL以及第二类吸附模型中由吸附模型计算的孔隙体积V0所知[17]。8 种吸附模型的吸附能力由高到低为优化D-R 模型>优化L 模型>优化D-A 模型>D-R 模型>L模型>D-A模型>优化T模型>T模型。
8 种模型的回归系数平方R2都大于0.950,并不能很好地评估出模型的适用性。因此,以标准差s与相对误差v为指标来进一步比较。标准差越小,相对误差越低,模型拟合精度越高。
标准差计算表达式[18]:
式中:s为标准差,cm3·g-1;n为压力点的数量;si为试验数据,cm3·g-1;为模型拟合计算值,cm3·g-1。
相对误差计算表达式:
式中:v为相对误差,%;vi为试验数据,cm3·g-1;模型拟合计算值,cm3·g-1。
36℃(309.15K)下等温吸附模型的标准差与相对误差结果如图5、图6所示,优化T模型、T模型、优化L模型、优化D-A模型计算后的标准差较小,相对误差较低,对于试验数据的拟合效果较好;优化DR 模型、L 模型、D-A 模型的标准差较大,相对误差中等,可以对煤样N2吸附进行拟合,但拟合效果中等;D-R 模型的标准差最高,相对误差较高,证明模为型对于N2吸附的拟合效果较低。
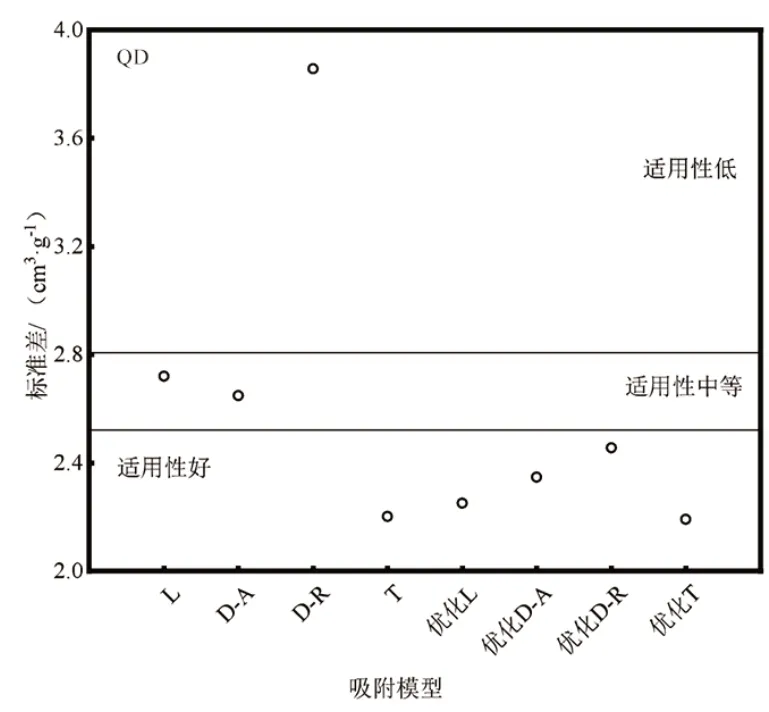
图5 36℃(309.15K)下等温吸附模型标准差Figure 5 Standard deviation of isothermal adsorption models at 36°C(309.15K)
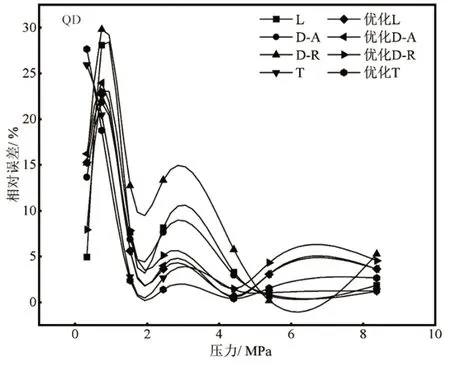
图6 36℃(309.15K)下等温吸附模型相对误差Figure 6 Relative error of isothermal adsorption models at 36°C(309.15K)
如图5、图6 所示,8 种模型拟合精度由高到低依次为优化T 模型>T 模型>优化L 模型>优化D-A模型>优化D-R 模型>D-A 模型>L 模型>D-R 模型;结合自由相密度与吸附相密度优化后的L、T、D-R、D-A 吸附模型对低渗煤中N2过剩吸附量拟合的结果与实验数据吻合程度较好。经分析,LZ 煤样也存在相同的结果。
如图4 至图6 所示,T 模型与优化T 模型的拟合效果优于其它模型。T模型是基于L模型的改进,对低渗煤中N2吸附具有很强的适用性,拟合的吸附量与煤的实际吸附过程吻合较好[19],因此T 和优化T模型具有较高的适用性;因为煤的孔径分布不是严格的正态分布,而是威布尔分布,D-A 模型比D-R模型的拟合效果更接近低渗煤中吸附N2的实际情况[20],因此D-A的适用性优于D-R模型;L模型作为气体分子均匀吸附在煤基质表面上的假设,当吸附剂表面各活性位点的吸附水平差异很大,煤的孔隙表面吸附能力不均匀时,适用性较差,随着压力的增加,这种不均匀性逐渐减小,模型拟合的适用性逐渐提高[21];D-R 模型假设N2分子根据微孔中吸附势的大小依次填充孔隙体积[22],具有较低的适用性。
4 结论
1)①两组煤样中N2吸附呈现类似吸附特征,符合经典IUPAC等温吸附分类标准中的第Ⅰ型等温吸附曲线,在2MPa 左右出现拐点;②N2吸附主要包括两个阶段:在0~2MPa 的低压力阶段,吸附量急剧上升;在2~9MPa 高压力阶段,吸附量趋于平缓;③QD与LZ样品等温吸附线在拐点(2MPa)之前,吸附量大致重合,在拐点之后,QD对N2的吸附量高于LZ。
2)8种模型吸附能力从高到低为优化D-R 模型>优化L 模型>优化D-A 模型>D-R 模型>L 模型>DA模型>优化T模型>T模型;
3)结合自由相密度与吸附相密度优化的L、T、D-R、D-A 吸附模型对低渗煤中N2过剩吸附量拟合的结果与实验数据吻合程度较好。
4)以回归系数平方R2、标准差s与相对误差v为指标,模型拟合精度由高到低依次为优化T 模型>T模型>优化L 模型>优化D-A 模型>优化D-R 模型>D-A模型>L模型>D-R模型。
