基于正交试验法的刚构拱组合桥稳定性参数分析
2023-11-09王柏荣
王柏荣
(中铁交通投资集团有限公司,广西 南宁 530201)
1 工程概况
龙溪大桥为连续刚构拱组合桥,桥跨布置为(109+220+109)m,全长为457.1 m。系梁横截面采用单箱双室变高截面,边支点断面高4.0 m,中支点断面高7.5 m,采用C55混凝土,拱肋为哑铃型截面,其中钢管直径为1.2 m,内部浇筑C55混凝土,两条拱肋之间间距为12 m。拱肋线形为二次抛物线,主拱矢跨为220 m,矢高为44 m。拱座采用钢筋混凝土结构,纵向长为13.5 m,横向宽为2.0 m,对应支点处箱宽加宽为1.6 m。
2 正交试验设计
2.1 正交试验法原理
正交试验法多用于解决多目标优化问题,此方法根据数理统计概率学的原理,基于正交性原理,优选出部分具有代表性的水平组合进行试验,在保证试验结果可靠和结论正确的前提下,使试验次数尽可能地减小,由于影响大跨度连续刚构桥稳定性的结构参数较多,全面试验次数费时费力,因此引入正交试验法大幅减小模拟次数,以获得最优的结构设计参数组合[1,2]。根据大跨度连续刚构拱桥的受力特点,结合工程背景,选取可能发生并会对结构实际状态产生较大影响的结构参数,根据施工控制经验确定各结构参数变化范围。其他条件不变的前提下,计算时仅改变单一参数,选取拱肋横撑形式、吊杆损伤程度、拱肋钢管壁厚度以及拱轴系数等影响参数,分析其对连续刚构拱组合桥空间稳定性的影响程度[3,4]。
2.2 目标评价函数建立
为了对大跨度连续刚构拱组合桥的空间稳定性进行优化分析,采用公式评分法,以结构屈曲稳定性系数作为评价指标,以优化原有设计方案为目标,建立评价目标函数K,见公式(1)。
(1)
式中:k0为结构屈曲稳定性;[k]为稳定性系数容许值,取5;K为评价目标评价函数。根据公式(1)可知,当K大于1时结构空间稳定性才满足使用要求,并且在确定的试验情况下,评价目标函数值越小,则稳定性能参数组合越好。
2.3 正交表设计及试验参数确定
正交试验法可以有效减少试验次数,选取拱肋横撑形式、吊杆损伤程度、拱肋钢管壁厚度以及拱轴系数作为正交试验的敏感性分析参数,并对其进行优化分析。各参数及水平设置见表1。
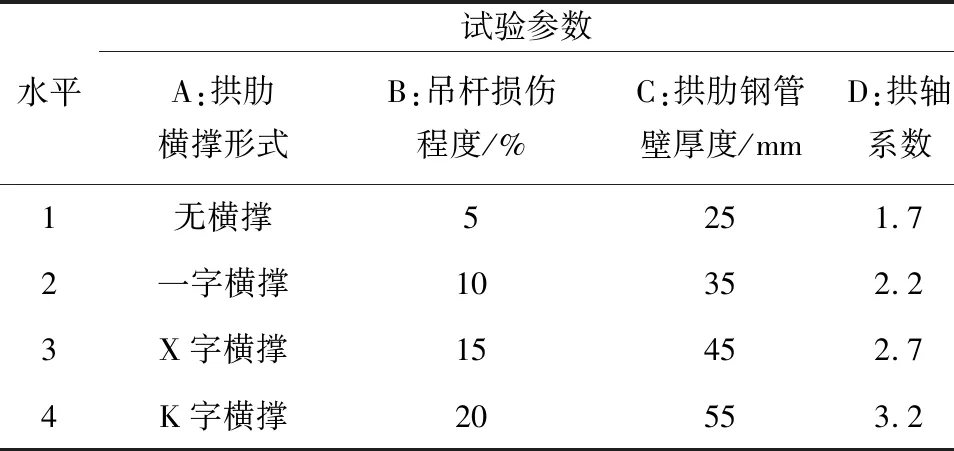
表1 影响参数及水平表
每个结构参数选取4个水平,若采用全面试验的研究方法,则需要进行256次试验计算才能完成结构参数的优化分析。选用L16(4×4)正交表,对优化参数进行试验设计,只需进行16次试验计算,L16(4×4)正交见表2。
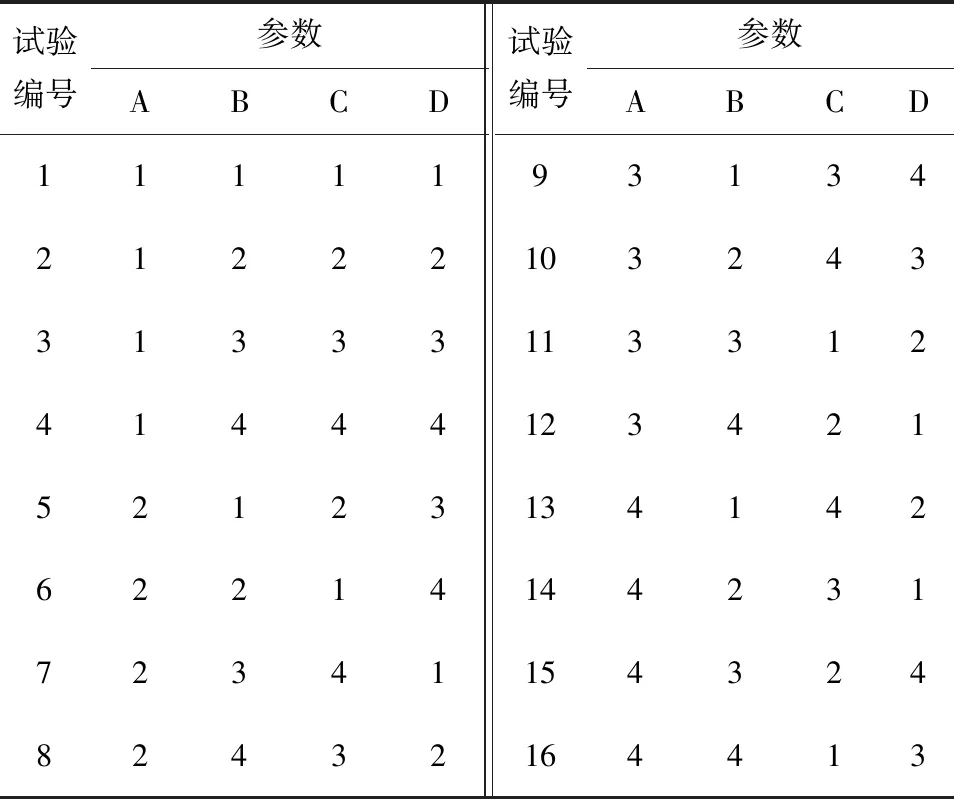
表2 L16(4×4)正交表
3 正交试验结果及分析
3.1 连续刚构桥有限元模型建立
根据工程设计图纸,按照桥梁结构的截面实际尺寸,考虑桥梁的实际施工情况,尽可能合理简化,利用数值分析软件建立全桥三维有限元模型[5]。力学模型的准确性,取决于是否能够对桥梁实际情况能够进行准确模拟,决定着桥梁结构所得分析结构的准确性。拱肋、支架钢管、立柱间的纵、横向连接采用空间梁单元模拟。连续刚构拱桥整体模型划分为5 283个单元和2 468个节点。将16组正交试验参数组合代入有限元模型中计算,正交试验数值模拟结果见表3。
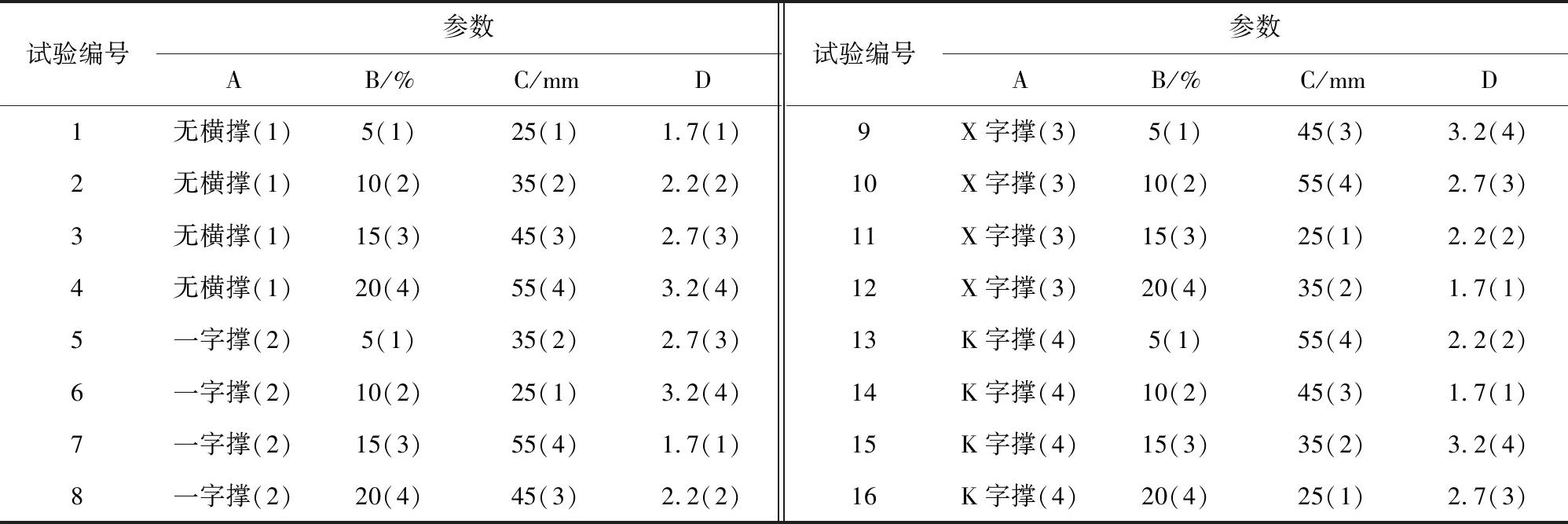
表3 L16(4×4)正交试验数值模拟结果
3.2 稳定性最优参数确定
根据表3中数据,结合公式(1)计算目标评价函数K值,结果见表4。
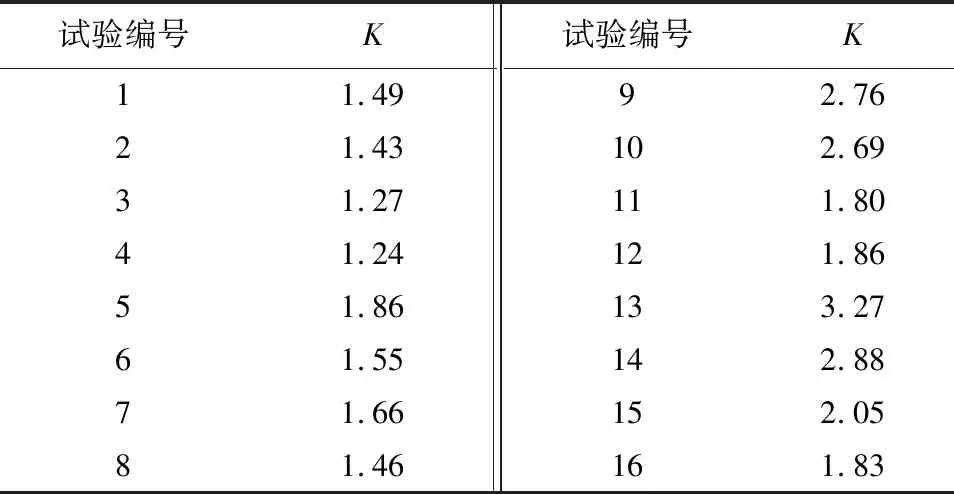
表4 综合目标评价函数K计算结果
由表4可知,9号A3B1C3D4、10号A3B2C4D3、13号A4B1C4D2以及14号A4B2C3D1试验组合K值较大,分别为2.76、2.69、3.27以及2.88。13号方案目标评价函数K=3.27最大,由此确定大跨度连续刚构拱组合桥稳定性最优参数组合为:K字形横撑,吊杆损伤面积5%,拱肋钢管壁厚度55 mm,拱轴系数2.2。
将试验组合K值最大的参数组合与原方案连续刚构桥的稳定性能进行对比分析,结果见表5,可知9号方案较原方案屈曲稳定系数增加了56.22%,10号方案屈曲稳定系数增加了52.15%,13号方案屈曲稳定系数增加了84.78%,14号方案屈曲稳定系数增加了63.12%,由此可知,13号方案结构参数组合最优,因此验证了该最优参数的选择正确性。
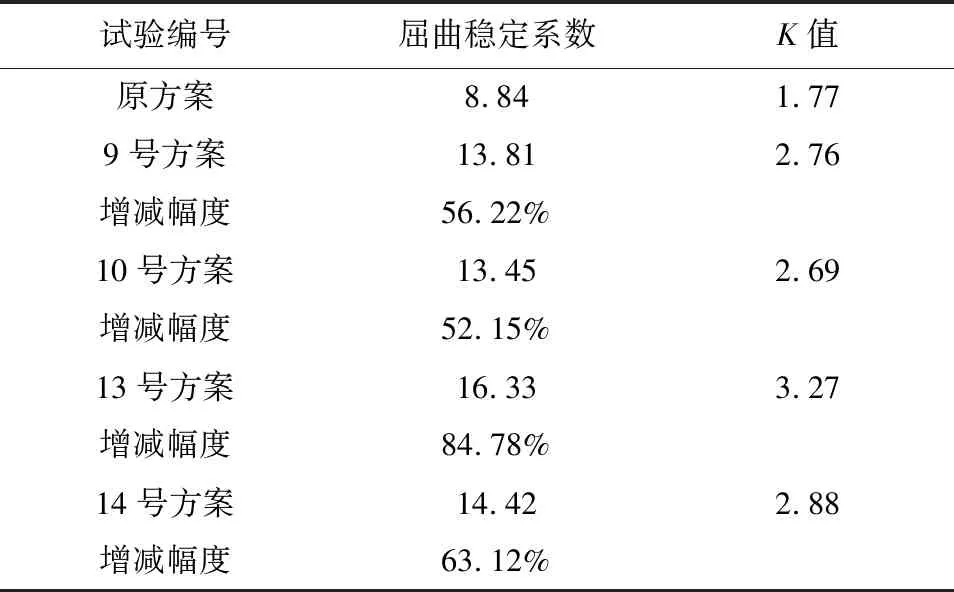
表5 优化方案与原方案对比
3.3 结构参数敏感性分析
为了获得结构设计参数对结构空间稳定性的敏感性及显著性,采用极差和方差分析方法对结构综合目标K进行分析。
3.4 极差分析
计算各项评价指标在不同结构设计参数下的极差分析结果,见表6。

表6 结构空间稳定性系数K极差分析表
通过表6可知,在结构空间稳定性系数K极差分析中,拱肋横撑类型极差R为目标评价函数的最大值,极差R为1.149。其次为吊杆损伤程度和拱肋钢管壁厚度,目标评价函数极差R分别为0.999和0.726,由此说明拱肋横撑类型对连续刚构拱组合桥的空间稳定性影响最大,其次吊杆损伤程度和拱肋钢管壁厚度也同样对连续刚构拱组合桥的空间稳定性影响较大,综合而言三种参数对刚构拱组合桥的空间稳定性都有着较为显著的影响。因此在设计过程中,合理选择拱肋横撑形式有利于结构的空间稳定性,保证结构安全性;对拱肋钢管壁厚度进行优化也可以提高结构的稳定性能。而在运营期间针对吊杆的力学状态也应时刻关注,同时也要关注吊杆防腐防锈,避免其力学性能的降低而导致吊杆损伤。拱轴系数极差R仅为0.105,说明拱轴系数对连续刚构拱组合桥稳定性敏感性程度微弱,因此对在进行结构空间稳定性优化设计时不需要调整拱轴线。综上所述,按照对连续刚构拱组合桥稳定性敏感性程度由大到小排序依次为拱肋横撑形式、吊杆损伤程度、拱肋钢管壁厚度、拱轴系数,即A>B>C>D。通过绘制评价指标-因子变化曲线,进一步分析各评价指标随不同的水平变化规律,见图1。
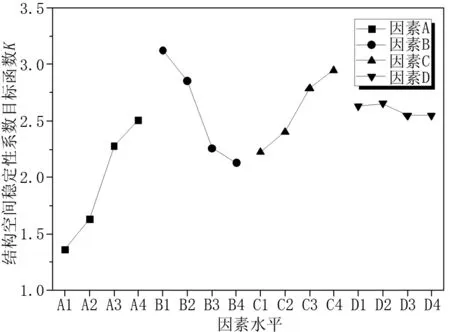
图1 评价指标-因子变化曲线
由图1评价指标-因子变化曲线可知,随着拱肋横撑类型的改变,结构的空间稳定性能变化幅度较大,其中拱肋间K字横撑和X字横撑对结构的空间稳定性能提升很大;而随着吊杆损伤程度的上升,连续刚构拱组合桥的结构空间稳定性系数逐渐下降,并且下降幅度明显。随着拱肋钢管壁厚度的增加,结构的空间稳定性能也随之提高,变化幅度呈现先提高后降低的趋势。由因素D变化曲线可知,提高拱轴系数对结构的空间稳定性能提升微弱,并且当拱轴系数增加到一定值时,结构稳定性能反而降低。因此由目标评价函数变化趋势可知,拱肋间横撑形式对连续刚构拱组合桥空间稳定性系数敏感性程度最大,而拱轴系数对结构稳定性能敏感性程度微弱。
3.5 方差分析
为进一步判断组合板梁桥各因素的显著性,对综合目标函数进行方差分析。表7为目标K下各因素离差平方和、自由度及平均离差平方和F值,通过与临界F值进行对比,对各因子影响试验指标的显著性做出判断。
由表7中目标评价函数K的方差分析可知,FA、FB分别为236.584和103.976,远大于F临界值29.5,说明横撑布置形式和吊杆损伤对连续刚构拱组合桥稳定性能影响非常显著;FC为51.76说明拱肋钢管壁厚度同样也对连续刚构拱组合桥稳定性影响显著。而FD为仅为1.386,远小于临界值29.5,说明拱轴系数对连续刚构拱组合桥稳定性影响微弱。综上所述,拱肋横撑布置形式对结构稳定性能影响最敏感,符合实际情况和上文中极差分析结果。
4 结 论
基于正交试验确定了大跨度连续刚构拱组合桥稳定性最优参数组合为:K字形横撑,吊杆损伤面积5%,拱肋钢管壁厚度55 mm,拱轴系数2.2,较原设计方案稳定性系数提高了63.12%。
进一步采用方差分析法验证了极差分析中的敏感性参数结果,即拱肋横撑布置形式对连续刚构拱桥稳定性能影响最敏感,敏感性程度由大到小排序依次为拱肋横撑形式、吊杆损伤程度、拱肋钢管壁厚度、拱轴系数,符合实际情况和上文中极差分析中的结果。
