高密度电阻率法在土质边坡渗流试验中的应用
2023-11-08吕海建赵自豪康森张云松李杰
吕海建,赵自豪,康森,张云松,李杰
(内蒙古科技大学 矿业与煤炭学院,内蒙古 包头 014010)
露天矿山的开采给我们带来资源,为我国的发展提供最基础的能源,但同时由于开采深度的增加,露天矿边坡的稳定性逐渐成为一个影响矿山安全生产和经济效益的问题.在降雨时,由于雨水沿裂隙渗入土体,导致土体稳定性降低,从而对边坡造成不利影响.上述问题在矿山开采边坡和排土场边坡中均存在,且由于排土场土体松散,其稳定性问题也更为严重.鉴于排土场边坡属于松散堆积体,其内部结构已知,且较开采边坡相对不稳定,因此便于通过试验来研究渗流条件下排土场边坡的稳定性变化.
降雨入渗是诱发边坡失稳的主要因素[1-2],研究渗流对边坡稳定性影响具有重要意义.在方法上,吕刚等[3]建立排土场平台-边坡室内模型,采用人工模拟降雨试验研究不同降雨强度和土体裂缝深度条件下排土场平台-边坡模型的演变过程,认为模型系统径流量和侵蚀量来自土体裂缝和降雨强度的共同作用;张岩岩[4]在分析降雨作用于斜坡时,同时考虑坡体的入渗和坡面的径流,研究表明,降雨强度较大时径流出现较早,降雨强度较小时渗流出现较早,且随时间的增加,小降雨强度作用下坡体水平位移具有更明显的响应;蓝宇[5]采用数值模拟方法对李屋排土场边坡稳定性进行综合分析,提出“分台阶排土+堆置反压平台”的治理措施,为矿山开采提供了安全保障;孙钦同等[6]将高密度电阻率法应用于坝体渗漏的探测,经过分析,表明高密度电阻率法对小范围和小渗流量的渗漏部位的探测具有很好的效果,能快速准确地定位渗漏部位.
目前在研究边坡稳定性的方法中,采用物理模型或数值模型进行分析的较为普遍,而使用仪器探测的较少,一方面由于排土场处于使用阶段,探测时排土体应力变化会对仪器带来干扰,影响数据的准确性;另一方面,出于安全问题的考虑,在探测时矿山往往处于停产检修阶段,探测的时间间隙极为有限.此外,由于实际矿山排土场边坡较大,通过实际排土场边坡研究渗流易对边坡造成不利影响,因此,搭建相似模型模拟渗流条件下不同时期边坡的状态,以此对照实际边坡变形的不同阶段,这种研究方法可为边坡治理提供参考.
本文通过建立某矿排土场相似模型,采用高密度电阻率法,对边坡模型在降雨渗流过程中的变化情况进行探测,经过分析,其反演视电阻率图像的变化与边坡模型裂隙的变化相吻合,表明高密度电阻率法能较好地反映模型边坡渗流的过程以及边坡裂隙的发展,为相关边坡稳定性的研究提供了一种思路.
1 研究方法
1.1 排土场边坡模型
以白云鄂博西矿排土场为原型,建立相似模型进行试验[7].模型采用长×宽×高为1.0 m×1.0 m×0.7 m的木制框作为试验装置,木框壁厚为1.6 cm.试验用土取自某建筑工地,试验用沙为普通河沙,取回的土经过1 mm孔径网筛选.搭建模型时,将小颗粒石块选出,模型按照土、河沙、小颗粒石块质量比为5.5∶3.0∶1.0进行配比.根据前人研究[8-9],结合实际排土场尺寸与试验模型条件,设定模型相似系数为40.填土时,模拟实际排土场排土情况,采用逐层压实的方法从下往上依次堆叠,模型搭建完毕后,其高度为50 cm,边坡角为自然安息角32°,顶部平台宽度约20 cm.边坡模型如图1所示.

图1 排土场边坡模型
1.2 高密度电阻率法原理
高密度电阻率法在工程物探中应用较为广泛,是直流电法的发展,其原理与常规电阻率法完全相同,即利用各种岩土之间的导电性差异,通过观测和研究与这些差异有关的人工电场分布规律,达到查明地下地质构造或寻找矿产资源的目的[10].以高密度电阻率法的温纳装置为例,说明高密度电阻率法的工作流程:探测前先将高密度电阻率法所用到的所有电极按一定顺序排列,并确保相邻电极间距离相同,以此形成一条完整的测线;测量时根据实际测线数量及电极间距设置仪器参数,包括电极间距、最小隔离系数、最大隔离系数、开始电极号、电极总数等.仪器工作时,有4个电极同时有电流通过,设这4个电极依次为A,M,N,B电极,其中电极A,B为供电电极,电极M,N为测量电极,测量时相邻电极间有AM=MN=NB的距离关系[11].每测量一个点后电极编号都会变化,通过不同电极的组合,最后所有电极都有电流通过.图2为高密度电阻率法工作流程示意图,其中a为相邻电极间距,n表示测点的层数,图2中共有5层测点.根据隔离系数的设置,图2中最大隔离系数为5,表示电极A与M之间间隔5个电极,即若电极A为1号电极,则电极M为6号电极,电极N为11号电极,电极B为16号电极,依次类推.根据高密度电阻率法仪器原理,温纳装置的跑极方式被称为逆向斜测深,测量时电极A的位置不变,隔离系数由大变小,故电极的间距也逐渐变小,测量的深度逐渐变浅,最后电极到达相邻电极,即A为1号电极,M为2号电极,N为3号电极,B为4号电极,此时每层测点第一个点的视电阻率均被测量.接下来以2号电极为A电极,按照前述方法依次测量,测量完毕后得到一个倒梯形的探测断面.

图2 高密度电阻率法工作流程
试验采用DUK-2B高密度电阻率法测量系统,所用测线共有30个电极,故本试验共有9层测点,每次测量测点总数为135个.根据边坡模型尺寸,测线沿模型顶部平台走向布置,距离边坡模型后缘15 cm,初末两电极距模型两侧各约4.7 cm,电极间距为3 cm,电极插入模型深度为3 cm.高密度电阻率法测量系统外接25 V电源,使用温纳剖面,设置最大隔离系数为9,最小隔离系数为1,开始电极号为1,电极总数为30,供电时间为0.5 s,其他参数均为默认值.设置完毕后进行接地检测,避免出现接地电阻过大而无法测量的情况,检测完毕无异常后即可开始测量.测量时第一个测点的电极号为1号、10号、19号、28号,4个电极同时有电流通过,所得电阻率为探测断面左下角第一个数据的视电阻率,后续测点的电极号按前述方法依次排列.
测量完毕后导出所测数据,由于测量时测点数据为电压(mV)、电流(mA)、视电阻率(Ω·m),而RES2DINV反演软件可识别的数据为测点的横坐标(m)、纵坐标(m)、视电阻率(Ω·m),故需对导出的数据进行转换以便反演软件识别.之后采用RES2DINV反演软件对转换后的数据进行反演处理和校正[12].经实测数据分析,随深度变化层厚增加系数取1.1较为合适.不同层厚增加系数条件下反演数据迭代误差如图3所示,以第1次集中降雨中第1分步降雨所测量的数据为例,从图3可以看出,层厚增加系数取1.1时,迭代RMS误差为7.4%;层厚增加系数取1.25时,迭代RMS误差为7.6%,故层厚增加系数取1.1较为合适,其误差较小.在此条件下,由于仪器因素,测量深度为测线长度的1/6,为0.144 m,故模型反演视电阻率的最大深度也为0.144 m,如图3a所示.图3中左侧纵坐标表示反演深度,下部横坐标表示测线电极相对位置及电极距,为便于定位电极,取1号电极对应横坐标为0.03 m,2号电极对应横坐标为0.06 m,依次类推,30号电极对应横坐标为0.90 m.

图3 不同层厚增加系数条件下反演数据迭代误差
1.3 降雨装置
为模拟局部降雨,采用滴灌装置在边坡顶部进行降水.试验中共设置8个滴箭,各滴箭间距约为11 cm,滴箭与主水管之间用短软管连接,主水管连接水泵.试验时移动滴箭,使水均匀滴在边坡模型顶部,同时避免产生径流.
2 试验过程与结果分析
2.1 试验设计
试验采用“模拟降雨—停止降雨并测量—再次模拟降雨—再次停止降雨并测量”的循环模式研究高密度电阻率法在渗流试验中的应用,该方法可通过高密度电阻率法的反演图像观测边坡模型内部视电阻率的变化情况,再根据视电阻率的变化推断出边坡内部裂隙的产生及变化.试验以0.62 mm/min的降雨强度进行2次集中降雨.第1次集中降雨时,开始每分步降雨持续3 min,间隔10 min,由于边坡模型初始含水量较少,雨水入渗较快,分步降雨4次后,调整每分步降雨持续时间为5 min,间隔15 min,共进行19次分步降雨;将边坡模型在通风环境下静置12 h后,进行第2次集中降雨,其每分步降雨持续时间为5 min,间隔15 min,共进行13次分步降雨.分步降雨间歇期使用高密度电阻率法仪器测量边坡内部断面,得到视电阻率数据.
2.2 第1次集中降雨反演视电阻率变化
第1次集中降雨第1分步降雨时,以0.62 mm/min的降雨强度模拟降雨3 min,降雨时移动滴箭使雨量均匀.3 min后停止降雨,按前述值设置DUK-2B高密度电阻率法测量系统参数并测量,测量完毕后确认仪器所测量的测点个数,无误后确认该次测量数据有效.第1分步降雨结束10 min后进行第2分步降雨,降雨条件与第1分步相同.第4分步降雨结束后,延长间歇时间至15 min,并调整第5分步降雨时间为5 min,且后续分步降雨以该时间为标准,共进行19次分步降雨.
取反演视电阻率变化较为明显的第1分步、第13分步和第17分步降雨后所测量的数据(如图4所示)进行分析,说明高密度电阻率法在渗流试验中的应用效果.图4a是第1次集中降雨第1分步降雨后模型的反演视电阻率,由图4a可知:视电阻率大致呈层状分布,且由浅至深视电阻率逐渐增大,反演视电阻率较为均匀,无高、低阻体异常出现.说明在均匀地层中,雨水下渗均匀,表现为在反演图中视电阻率由浅至深均匀分层变大.
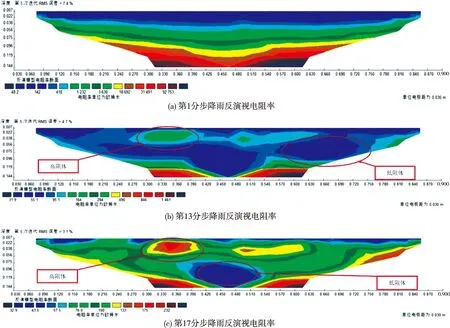
图4 第1次集中降雨边坡视电阻率变化情况
由图4b和图4c可知,随着降雨继续,边坡模型中逐渐出现视电阻率高、低阻体异常现象.图4b中,在断面横坐标为0.30~0.39 m,纵坐标为0~0.06 m处出现高阻体,最大视电阻率约为165 Ω·m;在断面横坐标为0.57~0.72 m,纵坐标为0~0.11 m处出现低阻体,最小视电阻率约为32 Ω·m.图4c中,在断面横坐标为0.30~0.39 m,纵坐标为0.01~0.05 m处出现高阻体,最大视电阻率约为175 Ω·m,且其周围视电阻率整体变大;在断面横坐标为0.42~0.51 m,纵坐标为0.09~0.14 m处出现低阻体,最小视电阻率约为33 Ω·m,与图4b相比,原有低阻区变得不明显,说明模型内部由于渗流处在动态变化的过程中.从第1次集中降雨开始到结束,反演视电阻率图中所表现出的边坡模型表面变化与肉眼所见基本一致,但比肉眼所见更为精确,边坡微小裂隙产生时并不明显,但反演视电阻率图中却有体现.随着降雨的进行,裂隙越来越宽,反演视电阻率图中相应位置也呈现出较大的视电阻率,边坡表面的微小裂隙逐渐延伸,如图5所示.

图5 边坡表面产生的微小裂隙
降雨过程中边坡内部出现高、低阻体异常现象.高阻体异常表明边坡内部微小颗粒物随水流进入到边坡更深处,导致原有位置出现的空隙被水充填并与大颗粒沙石形成新的结构,使电阻变大;而低阻体异常表明随水流移动的微小颗粒物越来越多,阻力也越来越大,并逐渐在边坡更深处聚集,阻挡了细微颗粒物的继续移动,由于入渗雨量小,以致边坡原有结构中的空隙被细微颗粒物充填,从而变得更为致密,使得岩土体结构发生改变,入渗的水更多地与沙土混合,形成低电阻异常体.
2.3 第2次集中降雨反演视电阻率变化
第1次集中降雨结束12 h后,进行第2次集中降雨.第2次集中降雨中每一分步降雨持续时间为5 min,两分步降雨的间歇时间为15 min,降雨强度0.62 mm/min,共进行13次分步降雨.取反演视电阻率变化较为明显的第2次集中降雨前、第1分步、第7分步及第10分步数据分析裂隙的变化情况.
第1次集中降雨结束,将模型在通风环境下自然风干12 h后,使用高密度电阻率法仪器测量模型边坡内部视电阻率变化,如图6a所示.经分析,其反演视电阻率图显示出边坡视电阻率异常区域与第1次集中降雨后期变化不大,但浅部高视电阻率区域有横向贯通趋势.

图6 第2次集中降雨边坡视电阻率变化情况
第2次集中降雨第1分步降雨后反演视电阻率如图6b所示.该次降雨后,模型的高、低阻区变得清晰,高视电阻率区域位于断面横坐标0.42~0.51 m,纵坐标0.03~0.06 m处,最大视电阻率约为200 Ω·m.
第2次集中降雨第7分步降雨后反演视电阻率如图6c所示.随着降雨的进行,边坡内部高阻体延伸至边坡表面,表明更大颗粒物随水流沿已有裂隙进入边坡内部更深处,导致原有位置空隙增大并失去原有稳定性,内部裂隙逐渐与表面已有裂隙连通,形成贯通裂隙,高视电阻率区位于断面横坐标0.42~0.51 m,纵坐标0~0.07 m处,最大视电阻率约为220 Ω·m,此时高阻体连通.
第2次集中降雨第10分步降雨后反演视电阻率如图6d所示.随着降雨继续进行,边坡表面其他位置的颗粒物随水流进入已有裂隙,由于边坡内部深处水流不畅,颗粒物在裂隙处逐渐堆积,导致裂隙闭合,延伸到边坡表面的高阻体视电阻率逐渐变小,其最大视电阻率约为100 Ω·m.岩土体结构继续改变,边坡的不稳定性增加.
3 高密度电阻率法在边坡渗流试验中的应用效果分析
3.1 高密度电阻率法具有较高的灵敏度
高密度电阻率法是利用各种岩土之间的导电性差异实现探测,在本试验中,由于渗流产生裂隙,岩土体空隙增大,导致两电极之间电阻率变大,这种现象反映在反演视电阻率的高阻体异常上.尽管裂隙较小,但高密度电阻率法仍能发现异常,这说明在小模型中高密度电阻率法也能体现出良好的探测效果.
3.2 高密度电阻率法能准确探测边坡模型内部裂隙
研究渗流时,在边坡模型表面只能观察到随渗流的进行边坡产生裂隙,但不知道裂隙多深,也不知道边坡内部有没有裂隙,而使用高密度电阻法,通过视电阻率异常可以直观地知道边坡内部情况,也能通过电极位置找到具体的异常点,为掌握边坡内部的变化情况提供依据.图7为模型断面横坐标为0.48~0.51 m处第一层测点的视电阻率变化情况,对应测量电极号为16号和17号,该处由于渗流产生较大裂隙,视电阻率波动较大.如图7所示,第1次集中降雨开始时,由于岩土体较为干燥,视电阻率较大,随着降雨渗流的进行,视电阻率逐渐减小,直到第1次集中降雨结束视电阻率达到最低;静置通风12 h后,岩土体变得相对干燥,视电阻率又升高,但比初始时要低;继续进行第2次集中降雨,发现视电阻率经历“减小—升高—减小”的过程,此时肉眼可见该处裂隙经历“闭合—裂开—闭合”的循环,但闭合未能达到边坡最开始时无裂隙的情形.边坡其他测点同样能通过提取测量数据绘制图表来展示其视电阻率变化情况.
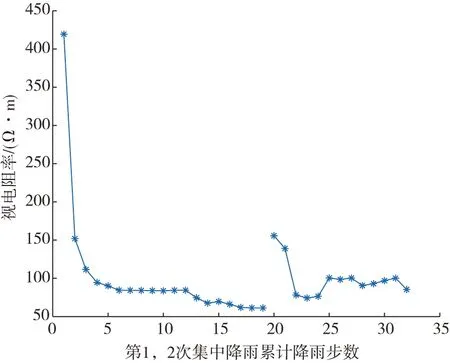
图7 电极号16号和17号处第1层测点视电阻率变化
3.3 高密度电阻率法可实现对裂隙的持续探测
通过试验可知,随着降雨的进行,边坡模型反演视电阻率发生相应变化,并且不同分步降雨后反演视电阻率异常区域呈现一定的连续性,通过这些变化可以分析边坡模型裂隙产生的部位、大小、延伸方向等,及时发现边坡隐患,为治理边坡隐患提供参考.
4 结论
1)高密度电阻率法对边坡模型内部变化的探测非常敏感,可用于微小裂隙的探测,在小型有限空间中也同样适用.
2)采用“降雨—探测—降雨—探测”循环的方式探测边坡微小裂隙的产生、发展等变化情况,探测的反演视电阻率结果与模型实际裂隙变化情况吻合,表现为有裂隙处反演视电阻率相对较大,无裂隙处反演视电阻率相对较小.
3)降水渗流使边坡产生裂隙,裂隙处经过“裂开—闭合—裂开—闭合”的过程,导致裂隙逐渐变宽,增加了边坡的不稳定性.
4)采用高密度电阻率法探测时,测点电极布置于边坡表土层,尽可能地避免了对边坡内部结构的破坏;同时从试验结果来看,渗流裂隙未在电极处产生或延伸,说明仪器设备对试验结果的干扰较少.因此,该方法在露天矿山边坡稳定性的探测上具有很强的实用性.
