基于线性SVM算法的云数据中心蓄电池状态预测
2023-11-08杨玉丽李培仁李学智马彦楷
杨玉丽,李培仁,李学智,马彦楷,李 震
(1.昆仑数智科技有限责任公司,北京 102206;2.清华大学 航天航空学院,北京 100084)
0 引 言
阀控铅酸蓄电池广泛应用于云数据中心供电系统,蓄电池组作为数据中心的短备电源,是数据中心供电系统最为核心的部件,可以保证数据中心内信息系统和应急照明等重要设备的不间断供电。蓄电池故障是云数据中心运行管理的主要风险[1]。阀控铅酸蓄电池老化对云数据中心供电可靠性构成重大威胁[2]。蓄电池的老化程度影响蓄电池的容量和使用寿命[3-4]。蓄电池老化有很多原因,包括板栅腐蚀、酸雾泄漏、失水过多、热失控、干涸发热等[5],蓄电池老化的现象是内阻的增加和容量的降低[6]。
国内外对于阀控铅酸蓄电池在线监控系统进行了大量研究[7-15]。研究主要集中在两个方面:一是电池测量系统,通过电压、内阻和温度对电池荷电状态进行准确估算,为电池是否需要充电提供参考;另一个是电池健康状态的诊断和预测,为电池是否需要更换提供参考。电池健康状态的诊断和预测有硬件设计和仿真、算法研究等。相关研究证明阀控铅酸蓄电池的健康情况与内阻有关,通过对阀控铅酸蓄电池内阻的预测能够得到蓄电池状态的预判[16-17]。
云数据中心供电系统对于电源的可靠性要求高。但云数据中心场景下的蓄电池故障诊断和预测研究并不多,LI 等研究了基于蓄电池电压和内阻历史数据的蓄电池故障诊断算法[18]。该研究基于蓄电池电压和内阻历史数据,提出了利用拉依达准则进行的故障诊断方法,这种方法不但能使诊断提速,而且当多个电池同时发生故障时不存在误诊情况,侧重于实时诊断。对蓄电池状态的预测能够在实时诊断的基础上降低运行风险,给云数据中心运行管理带来更多的灵活性。
本文针对云数据中心阀控铅酸蓄电池在线监控,提出了基于线性SVM算法的阀控铅酸蓄电池状态预测方法。
1 预测方法的建立
首先,截取蓄电池运行时的内阻数据。由于生产环境因素导致监控采集数据存在一定噪声,因此需要对数据进行平滑处理。
1.1 高斯滤波器平滑数据
将电阻的最高点作为中间端点,对电阻数据进行滤波,以保证电阻达到最高值的时间不变,取得平滑后数据。
二维高斯滤波函数[19]为
(1)
1.2 机器学习算法
将数据分成模型训练数据和预测数据2组,利用经典机器学习算法进行建模预测,分析内阻数据故障变化特征。提取特征后,使用相同的机器学习算法建模预测。比较2次预测结果,找出适合云数据中心蓄电池状态预测的特征值和机器学习方法。本文使用的6种机器学习算法如下:
1) 决策树。
G(D,a)=E(D)-Enew(D)=E(D)-
(2)
式中:E为分类所需的信息量;D为每类的实例;pk为样本属于分类的概率;a是实例的属性;G为熵的期望压缩。决策树可以逼近离散函数值[20-22]。
2) 线性判别。
g(x)=ωTx+ω0
(3)
在两类{ω1,ω2}问题中,x表示m维输入空间中的样本;ω为决策平米的法向量。此算法的主要特征是同一类的高维数据投影到低维空间后相同类别地聚在一起,不同类别之间相距较远[23]。
3) 朴素贝叶斯。
P(X|Y)=P(Y|X)P(X)/P(Y)
(4)
式中:X是一个随机事件,P(X)是X的先验概率;Y是训练样本,P(Y)是通过对Y的观测得到的先验概率。此算法可在假定给定目标值时属性之间相互条件独立,简化了实际应用场景中的复杂性[24]。
4) 线性SVM。

(5)
式中:ω∈Rn是超平面的法向量;γ是一个实数;A是数据点矩阵,e∈Rm是分量全为1的向量。此算法可用一个超平面尽可能远地分离正反例数据[25-26]。
5) KNN。
(6)
式中:D是全体维数的样本;r是一个子集;k是最近的样本数量;a、b分别为两个样本。此算法可依据最邻近的1个或者几个样本的类别来决定待分样本所属的类别[27-28]。
6) 神经网络。
(7)

2 蓄电池状态预测实验
2.1 数据采集设备
EMERSON电池监控仪:型号BM-42,内阻监测范围0.1~35 mΩ,测试精度±2%;单体电压监测范围0~16 V,测试精度±0.1%。
2.2 实验方法
2.2.1 数据准备
数据来源:某能源企业大型数据中心阀控铅酸蓄电池运行时的内阻数据。阀控铅酸蓄电池型号:FLAMM 12FLB450。数据采集频率:1次/15 min。数据周期:第5~7年的运行实测数据。
由于传感器、电池自身特性等原因,内阻会出现波动,故使用高斯滤波器光滑数据。
2.2.2 记录方法
1为蓄电池故障状态,0为正常蓄电池。1∶0表示真实值为故障电池,预测值为正常电池。1∶1、0∶1、0∶0以此类推。
准确度=真实值与预测值一致的电池数量/参加预测的电池数量×100%。
2.2.3 实验流程
选取实验电池电阻数据,对数据进行平滑去噪并分别进行2组实验:第1组先进行机器学习建模预测,再与6种经典算法预测结果进行对比;第2组先提取特征值,再进行机器学习建模预测,然后与6种经典算法预测结果进行对比。通过以上实验对比,选出1种较优算法增加训练数据预测,得到最终预测结果。
2.3 实验过程
1) 选取698个电池电阻数据(取值频率为15 min,周期为6个月),其中266个为故障电池,432个为正常电池。500个为训练数据集,198个为预测数据集。测试数据集中60个为故障电池,138个为正常电池。
2) 对698个电池内阻数据进行高斯滤波器平滑去噪。蓄电池在运行过程中的阻值记录曲线都存在一定振幅的波动,见图1。图1(a)、(b)分别为正常蓄电池1号、2号内阻随时间变化曲线,在±0.2振幅范围内波动,差异量数较均衡。图1(c)、(d)分别为故障蓄电池3号、4号内阻随时间变化曲线。可以看出,曲线斜率增大,存在1个或n个波峰。可见故障蓄电池阻值曲线具有明显峰值、斜率陡增、在一定周期内出现多个波峰等特征。
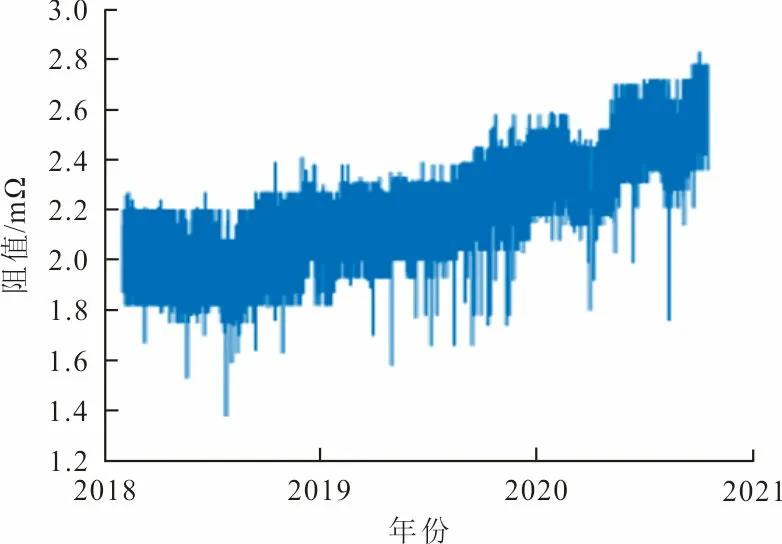
(a) 1号蓄电池

(b) 2号蓄电池

(c) 3号蓄电池

(d) 4号蓄电池
图2为3号蓄电池平滑前后数据对比。可以看出,通过高斯滤波处理后,数据与原数据的波动特性、趋势保持一致。
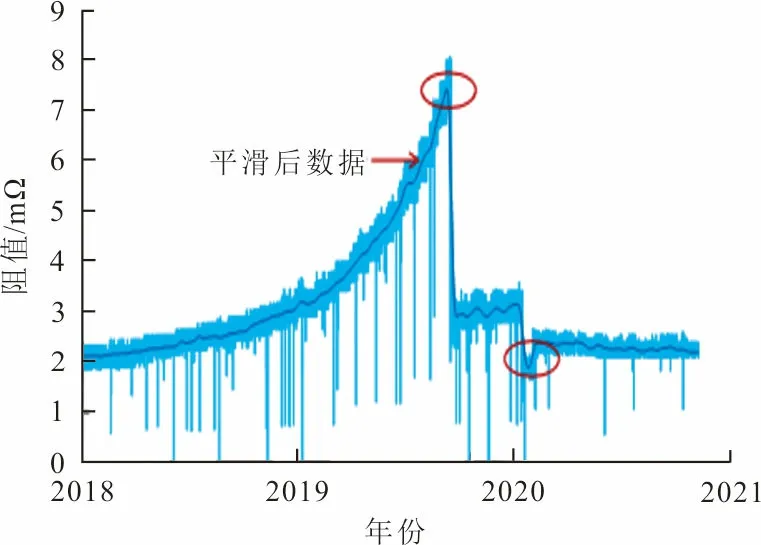
图 2 平滑前后数据对比Fig.2 Comparison of data before and after smoothing
3) 选取6种经典机器学习分类方法。
4) 使用机器学习分类方法,预测198个电池是否会出现故障,记录预测准确率。
5) 对500个电池内阻数据进行训练,提炼特征值,记录特征值。
表1为电池特征值训练结果统计。其中,A为6 h内最大内阻值,取6 h内不同时间测得电阻的最大值。B为3个月内光滑后的电阻值随时间变化的平均斜率。C为一年内光滑后电阻,其斜率下降区间的时间占比。D、E为二次函数y=ax2+bx+c的系数,S为二次函数y=ax2+bx+c的拟合方差。最小值是指特征值全部训练结果中最小数据;最大值是指特征值全部训练结果中最大数据;范围是最大值与最小值之间的距离;平均值是某一特征全部训练结果之和/数量;标准偏差是特征值训练数据的标准差;偏斜度是特征值数据分布的不对称指标;峰度是特征值数据分布曲线峰顶尖锐程度。从表1可以看到:特征A数据值跨度较大,在[1.82,7.9]之间跳跃显现;特征B数据值集中在[-0.69,1.49]之间,分布曲线峰度最小;特征C数据值在[0.00,0.92]之间,取值范围0.92,各个数据值之间取值范围最接近;特征D、E数据值取值范围较大,分布曲线峰度最尖锐;特征值S在[1.38,6.70]之间,取值范围5.32,出现负偏离,峰度较缓。通过训练后,故障电池特征的描述增加了维度和层次。

表 1 特征值训练结果统计
蓄电池电阻特征值数据具有空间分布性质,如图3所示。可以看出,A、B、C3个特征值在三维空间的离散分布表现为故障数据、正常数据分别聚合,大部分故障数据和正常数据并不交叉,故障电池和正常电池在空间分布中能够找到一个分割平面进行区分。

图 3 特征值数据空间分布Fig.3 Spatial distribution of feature values data
6) 使用基于特征值的机器学习分类方法,预测198个电池是否会出现故障,并记录预测准确率。
7) 选取预测效果较好的模型,截取周期为一年的数据(198个电池数据),预测未来一个月电池状态(故障/正常)。
3 结果与分析
3.1 机器学习方法预测
通过6种机器学习算法进行故障预测。表2为6种机器学习方法状态预测结果。

表 2 6种机器学习方法状态预测结果
从表2可以看到,本实验按照过程4,198只电池内阻数据故障预测准确率在71.72%~81.82%之间,机器学习方法预测能够对提前判断蓄电池状态提供帮助。
3.2 提取特征值预测
通过训练特征值进行故障预测,6种机器学习方法故障预测结果的准确度在87.88%~96.46%之间,高于未提炼特征值预测结果10.10%~20.20%,见表3。其中,朴素贝叶斯算法和神经网络算法较未提炼特征值故障预测准确度提高10.10%,KNN算法较未提炼特征值故障预测准确度提高20.20%。
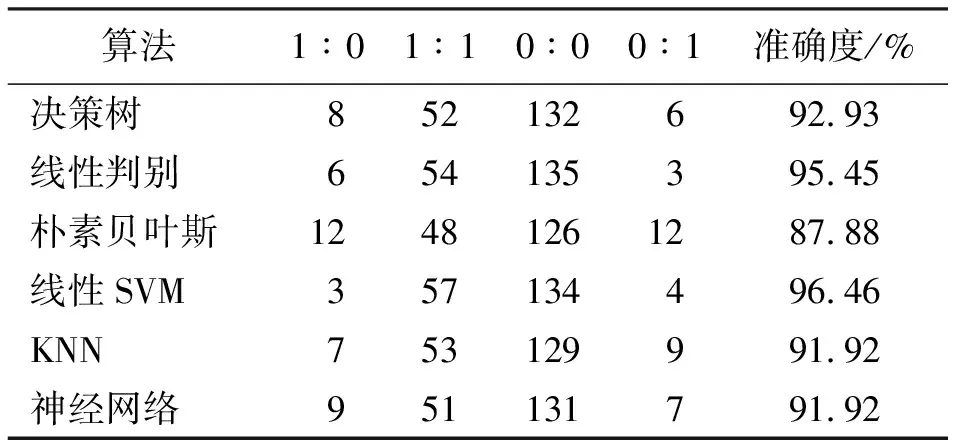
表 3 提取特征值状态预测结果
基于特征值的空间性质,线性SVM算法表现最好。线性SVM算法较未提炼特征值故障预测准确度提高17.68%,预测值与真实值一致的电池191个,故障预测准确度96.46%。其中将故障电池预测为正常电池数量为3个,占电池总数的1.5%,远低于其他算法将故障电池预测为正常电池比例。可以得出,合理的特征值能够提高预测准确度。
3.3 增加训练数据预测
使用线性SVM算法,将训练数据周期从6个月增加为1年,预测未来1个月电池状态(故障/正常)。预测结果如图4。可以看出,0∶0的电池134个;1∶1电池58个;0∶1的电池4个;1∶0的电池2个。
电池状态预测准确(真实值与预测值一致)的为192个,准确度为96.96%,较使用6个月电池数据准确度提高0.5%,较未提炼特征值预测准确度提高19.17%。电池真实状态为故障,预测值为正常的2个,占预测总数的1%。可见,增加训练数据可以提高准确率,但是误差仍然存在。
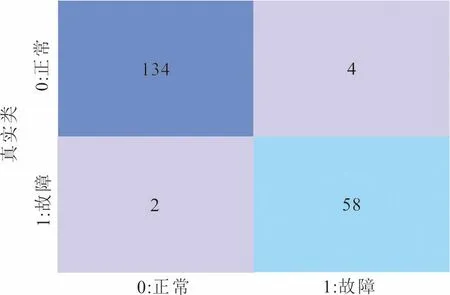
图 4 线性SVM故障预测结果Fig.4 Linear SVM fault prediction results
4 结 语
本文提出了基于经典机器学习算法的云数据中心蓄电池状态在线预测方法,能够在蓄电池实时状态监控的基础上,提前判断蓄电池状态。提取特征值,能够提高机器学习算法进行蓄电池状态预测的准确度。
基于线性SVM算法的故障预测方法在对生产环境运行第5~7年的蓄电池预测中准确率为96.96%,电池真实状态为故障,而预测值为正常的数量比占总预测电池的1%,在实际运行维护管理中有效降低了由于蓄电池老化带来的风险。对大型和超大型数据中心更换蓄电池具有实用价值。
本实验对象是在云数据中心环境下使用的阀控铅酸蓄电池,云数据中心环境相对实验室环境较为复杂,对其他影响电池老化程度的因素还需进一步深入探讨。
