基于数据纯度的模型博弈定价方法

江东，张小伟，袁野

1.东北大学，计算机科学与工程学院，辽宁 沈阳 110169

2.北京理工大学，计算机学院，北京 100081

引 言

随着物联网和移动网络技术的发展，各种工业自动化设备、移动设备产生大量不同类型的数据，这些数据越来越多地被视为珍贵资源。数据是新的石油资源，蕴含巨大价值[1]。由于数据产生于不同领域，因此导致了“数据孤岛”的产生。这不利于大数据产业的健康发展。为了解决该问题，提出了数据共享的概念，分为开放数据共享[2-3]和数据交易两种途径。开放数据共享是通过公用开放数据接口或者政府组织共享数据，可供分享的数据种类有限。数据交易是把数据推向市场，通过买卖方式共享数据。数据交易可以建立起一套规范的数据共享规则，使买卖数据双方都能够在该规则运行下得到自己想要的结果。在数据交易市场中，拥有数据的组织和公司可以通过交易得到相应回报，称为激励；而数据购买者也在其数据分析任务的驱使下，到数据交易市场购买数据。但是最初的数据交易市场仅提供原生数据，这要求许多数据购买者对数据自行加工，往往超出其能力范围。同时，由于数据产品相较于普通产品而言，其边际成本为0，即数据可以在成本趋近于0的情况下随意复制，导致使用传统的经济学方法对数据进行定价较为困难。因此一部分学者将研究重心从对数据的交易转向于对服务的交易。由数据平台收购原始数据，通过自己的加工对消费者提供相应服务并抽取一定佣金。

基于上述问题，Chen等人[4]提出了基于模型定价的概念。其核心观点是，市场不再销售原始数据给买家，而是提供不同精度选项的机器学习模型，即将数据定价转换为机器学习模型的定价。但提出的方法仅能够使卖方收益最大化，同时其提到的市场调查方法对于普通卖方来说过于复杂。Jia 等人[5]基于最近邻模型提出了定价方法，使用Shapley 值[6]来解决补偿的问题，但文章只注重数据平台和数据拥有者的交互。文献[7]提出的基于博弈论的模型定价方法虽然将数据市场的3个参与方都考虑在内，并实现了三方收益最大化，但文章设计的框架要求数据拥有者提供其收益函数，这在现实场景中往往不切实际。同时，数据质量作为模型效果最直接的影响因素，近来也吸引了相当的关注。但很少有文章将数据质量应用于模型定价当中。

为了弥补上述缺点，本文提出了基于数据纯度的模型博弈定价方法，注重数据市场3个参与方的交互。首先，在数据收集端，基于所收集到训练数据的质量和添加噪声数据多少两个指标提出了数据纯度的概念，并以其为依据对数据单位贡献进行补偿。由于数据纯度是基于数据真实的内在价值计算出来的，因此数据平台可以根据数据纯度提供给数据拥有者公平的补偿。其次，在数据出售端，数据平台根据模型购买者的购买意愿，以收集到的数据为基础，训练出符合模型购买者需求和数据贡献者隐私保护程度的产品，以平台收购数据的成本即补偿金额和模型训练成本为其定价基础，与模型购买者进行两阶段的Stackelberg博弈，以使得双方都能够达到收入最大化。

本文组织结构如下：第1节介绍数据市场和博弈论的相关概念；第2 节介绍问题的定义；第3 节对整个定价方法流程进行介绍，并对相关定理进行了证明；第4节通过实验证明了方法的有效性；第5 节介绍相关工作；第6 节对本文进行了总结。

1 相关概念

1.1 数据市场

在文献[8]中，数据市场被定义为任何人（或至少大量潜在注册客户）都可以上传和维护数据集的平台。数据的访问和使用通过不同的许可模式进行监管。通常情况下，数据市场定义为可以吸引拥有数据的客户和购买数据或服务的客户进行交易的平台或市场，该市场可以为拥有数据的客户提供补偿等服务，为购买数据的客户提供查询等服务，同时可以为双方进行匹配，并收取一定佣金。由上文可以看出，在数据市场中，主要包含数据拥有者、数据交易平台（简称数据平台）、数据或服务购买者3个参与方。

数据拥有者，或者称为数据卖家、数据提供者，负责向数据平台提供数据，并接受数据平台给予的相应补偿；数据平台也称为数据中间商、数据中介、经纪人等，负责对收购到的数据进行集成整合，设定数据收购价格并补偿数据拥有者，设定数据出售价格，为数据消费者提供查询其希望购买数据的接口和服务，给数据消费者提供数据并对出售的数据提供隐私、版权保护等任务；数据消费者又称为数据买家，在数据交易中需要完成的任务是向数据平台提出需求，并支付一定金钱从数据平台购买到自己所需的数据。

1.2 博弈论

博弈论是经济学中重要的研究方法，也称为对策论，是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题。博弈是指两个或者两个以上理性的个体或组织，在一定规则的约束下，参加一系列的竞争性行为，并且综合考虑对手可能实施的行为，在其基础上做出最有益于自己的决策。

博弈论中最为常用的一种博弈为Stackelberg 博弈，其应用场景如下：一个参与人（领导者）先行发布自己的价格策略，另一个参与人（追随者）依据领导者的策略做出相应策略选择，并进行优化，以得到最优的价格策略，这种模式被称为Stackelberg 博弈[7]。在Stackelberg 博弈中，参与人1（领导者）首先确定自己的价格策略v1，参与人2（追随者）在观察到v1后，确定自己的价格策略v2，该博弈属于完全信息动态博弈。由于参与人1（领导者）先于参与人2（追随者）行动，不能掌握v2的信息，所以对于参与人2（追随者）来说，其价格策略是一个从V1→V2的映射T。Haddadi 等 人[9]和Lv 等 人[10]证 明 了 使 用Stackelberg 模型可以让参与博弈的各方实现收入最大化。

1.3 差分隐私

差分隐私作为一种隐私保护手段，在模型交易市场中应用十分广泛。其正式定义如下：

给定两个近邻数据集D和D′，ε是一个正实数，A是一个随机算法，值域为Range(m)，其在数据集D和D′上任意输出结果x(x∈range(m))，且满足下面的不等式，则称算法A满足ε-差分隐私。

简单来说，该定义意味着满足差分隐私的随机算法输出结果在两个数据集上是不可区分的。而ε定义了这个不可区分的程度，可以看作是每个数据集的隐私损失上限。ε越小，输出结果的不可区分性就越大，隐私损失就越小。在本文中，数据平台训练的模型都是有差分隐私保证的，根据差分隐私对于后处理特性，模型购买者在收到模型后对模型进行任何后处理都不会产生额外的隐私损失[11]。

2 问题定义

在本文设计的数据市场中，参与者主要分为3 种类型：数据拥有者，数据平台和模型购买者。其中数据拥有者给数据平台贡献收集到的训练数据，同时提供自己能够接受的隐私保护水平，由ε定义，并接受来自数据平台的相应报酬；模型购买者向数据平台提交自己购买模型的意向精准度以及相应预算。数据平台负责将其收到的数据进行清洗、训练，并通过添加噪声方式满足数据拥有者的隐私保护需求，同时生成满足模型购买者精准度和预算的模型。数据平台在保证给予数据拥有者一定补偿和对数据进行清洗、训练的成本外，与模型购买者进行两阶段的Stackelberg博弈，最终使得双方收益最大化。

如图1 所示，首先，数据拥有者提供自己希望出售的数据及希望的隐私保护偏好值，数据平台根据数据及ε值计算数据纯度，并通过市场调查获得的数据纯度-价格的曲线，给数据拥有者提供相应的补偿。然后，模型购买者进行自己的调查，获得模型精度对应价值的曲线，并对数据平台提出模型购买需求。数据平台在收到购买需求后，为其训练模型并提供实例。然后模型购买者和数据平台进行两阶段的Stackelberg博弈，以获得最终成交价格，最后，双方进行交付。

图1 模型交易市场结构Fig.1 Structure of model marketplace

数据市场的参与者形式化定义如下：

定义1（数据拥有者）在本文中，数据拥有者定义为可以从各种来源收集到数据的组织或者个人，将n个数据拥有者定义为D1,…,Dn。每个数据拥有者Di可以提供的数据集定义为zi(i∈{1,…,n})，这些数据通常未经处理，存在冗余值、残缺值、错误值等数据质量问题，这些问题的存在往往会对训练出的模型精度产生较大影响。其次，在模型出售时，未对训练数据进行隐私保护处理可能会导致数据拥有者泄露隐私[11]。数据拥有者Di在出售数据时会事先拟定一个自己能够接受的最大隐私泄露程度，本文用差分隐私衡量，定义为εi。在数据平台收集数据时，数据拥有者将其拥有的数据zi和最大隐私泄露容忍度εi一同提交给数据平台。

定义2（模型购买者）文章将模型购买者定义为在数据市场中具有明确预算，希望购买相应精度机器学习模型的购买者。模型购买者需要向数据市场提供购买模型类型L，精准度acc和对应的单位精度预算Pc。

定义3（数据平台）数据平台负责从数据拥有者处收集数据，对数据进行评估、清洗最终训练模型。针对从数据拥有者D1,…,Dn收集到的数据z1,…,zn，数据平台依据完整度、冗余度和新鲜度三个维度对其进行打分，得分为Q1,…,Qn，并结合每个数据拥有者提交的εi确定对其的补偿Po。在完成数据收购后，数据平台依据补偿价值Po和模型购买者提交的精准度acc、单位精度预算Pc，与模型购买者进行两阶段的Stackelberg博弈，以获得最终成交价格。本文假设数据平台为可信平台，不会做出窃取数据拥有者隐私、故意操纵市场价格等行为。本文的符号与定义如表1所示。

表1 关键维度及对应指标Table 1 Key dimensions and corresponding indicators

3 基于数据纯度的模型定价

本文将数据市场的交易活动分为两个阶段：准备阶段和交易阶段。准备阶段主要是为了让数据平台和模型购买者进行市场调查。通过市场调查，可以让数据平台获得特定纯度下数据的收购价格，以便为自己收购数据奠定基础；同理，模型购买者通过市场调查可以获得在不同精度下模型的价值，以便对自己的收益进行预估。在完成准备阶段工作之后，正式进入交易阶段。

模型交易阶段主要分为两部分：数据收购端和模型出售端。数据收购端主要涉及数据拥有者和数据平台的交互；模型出售端主要涉及数据平台和模型购买者的交互。接下来将对其进行逐个介绍。

3.1 数据收购端

本文在同时考虑了数据拥有者和模型购买者需求的前提下，提出了数据纯度的概念。对于每个数据拥有者Di贡献的数据集zi来说，其数据纯度DPi定义如下：

其中，Qi为数据质量打分。该数据质量由3个维度组成：完整度Comi、冗余度Redi和新鲜度Redi。εi定义为每个数据贡献者的隐私偏好函数，该函数可以反映数据贡献者对其要出售数据隐私泄露的敏感程度。敏感程度越高，就要求数据平台向其中添加的噪声越多。更高的数据质量Qi和更大的隐私偏好εi都可以使得训练数据中对模型构建有积极作用的数据占比增高，即数据纯度增高。

数据质量分数。数据质量是影响机器学习模型质量的重要指标。为了创建一个通用的质量分数模型，本文采用了线性策略：

其中，ω1,ω2,ω3是权重参数，数据平台可以根据每次训练任务的要求自行设定，并通知数据拥有者。

对于属性完整度Comi来说，其定义为数据单元格中被分配了完整且有意义单元格的比例，即非空且数据在该属性值域范围内的单元格占总单元格的比例，计算公式为，其中error表示空值或无意义单元格个数；nor表示zi中单元格个数。冗余度Redi定义为数据集zi中重复记录的比例，计算公式为，其中dup表示与所有数据集重复的条目个数。最后，关于新鲜度的计算，本文参考了文章[8,12]的计算方法，文章认为对于数据集zi中的每个条目d来说，有关其新鲜度最重要的属性为（1）数据交付时间DT：即数据被收集到数据平台的时间；（2）数据最后更新时间LU：即数据最终被最后更新的时间；（3）数据有效期v。基于以上3种有关时间的描述，数据集zi的新鲜度Frei可以表示为：，其中nor为数据集zi中含有的条目个数。

隐私敏感分数。在本文设计的数据市场中每个数据拥有者在向数据平台出售数据时都需要设定自己对隐私泄露的敏感程度，用差分隐私参数εi表示。数据平台在收到数据后，向其数据集zi中添加相同格式的噪声数据，以满足数据拥有者的隐私需求。εi取值在(0,1)之间，添加的噪声越多，εi值越小，数据纯度越低。

在计算出质量分数Qi和隐私敏感分数εi后，便能得到归一化后的数据纯度DPi。由于更高的数据质量和更低的噪声水平都对应着更高的模型精度，因此数据纯度越高，其价值就越高，则数据平台就需要提供给数据拥有者更高的补偿。

对于数据平台来说，在得到每个数据拥有者Di提供数据的纯度打分DPi后，将数据纯度对应的精度公式设计为：

其中，acci表示在某种数据纯度的条件下，模型可以达到的最佳精度，β1，β2，β3为参数。同时，根据文献[13-14]提出的理论，模型精度和模型效用之间的函数关系应该具有子模性，即边际效用递减，因此将价值定义为V(acc) =σln(1+acc)。结合上述内容，某个模型的价值应该近似表示为数据纯度DP的线性形式。则数据平台对于其收购到数据集的补偿可以近似表示为：

3.2 模型出售端

在模型出售端，数据平台需要满足模型购买者的精准度需求，同时在模型购买者给定的价格下与其进行博弈，以使得双方收益最大化。因此应当首先定义双方的收益函数。

模型购买者的收益函数。模型购买者在购买模型之前，需要针对该次模型购买任务可以产生的价值进行调查，从而得到该模型在特定精准度下可以产生价值的估值函数V(acc) ，因此模型购买者的收益函数可以表示为该精度下模型可以产生的价值与其支付的价格之差：

在上式中，第一部分表示模型购买者通过收购数据模型进行特定任务能够产生价值的估值，第二部分是对该精度下的模型支付给数据平台的总额。本文假设估值函数V(acc) 是单调递增可微的严格凹函数，采用类似[13-14]中的效用函数：

该函数表示随着模型精度的增加，模型购买者能够从该模型中获得的效用也逐渐增加，但其增加速率随着精度的增加而降低。

数据平台的收益函数。在本文设计的数据交易市场中，数据平台的收益主要来自于模型购买者的支付，成本主要来自购买数据的支付和训练模型的成本。因此数据平台的收益函数表示如下：

其中，Pc*acc表示模型购买者的支付总额；Po表示购买该模型训练数据的花费；C(acc)表示构建acc精度下模型的花费，包括数据清洗、添加噪声和训练等任务。采用使用较多的二次函数来表示该代价函数C(acc)[15,16]：

其中，α≥0，β≥0。另外需要注意的是，训练代价C(acc)随着精度acc的增加而增加，同时，由于精度越高训练难度越高，因此其增长率也随之增加。

为了求解使得数据平台和模型购买者都能够达到收益最大化，本文构建了两阶段Stackelberg 博弈模型，以求得最优激励策略，模型购买者为领导者，数据平台为追随者。在博弈过程中，模型购买者首先根据收益最大化目标给定一个最优精度策略acc，数据平台根据该策略调整自己单位精度价格，以使得两者都达到收益最大化得目标。二者的目标函数为：

第一阶段模型购买者：

第二阶段数据平台：

定理1（数据平台的最优解）在第二阶段时，当模型购买者给定单位精度购买价格Pc的情况下，数据平台能够给出的最优精度策略为：

证明：证明采用逆向归纳法。

首先，将训练代价C(acc)=α*acc2+4β*acc带入到数据平台的收益函数中，可以得到：

在上式中，对acc求一阶偏导可得：

已知式（13）对acc的二阶偏导＜0，为严格凸函数，则在时取得的acc为最优解acc*，并且唯一。

定理2（模型买家的最优解）在第一阶段时，在数据平台给出最优精度策略acc*的条件下，模型购买者可以得到的最优价格策略为：

证明：首先，将式（7）中的V(acc)代入式子(6)中，同时，在数据平台取其最优解的情况下，将亦代入式（6）中，可以得到：

在上式中对Pc求一阶导并令其为0，即可得最优解。

4 实验与评估

4.1 实验配置与数据处理

实验设备为一台安装有ubuntu18.04的GPU服务器。该服务器配备了Intel Xeon Silver 4214 CPU 并且有128G 主机内存，4 个NVIDIA RTX 2080Ti。使用的机器学习模型是简单的逻辑二分类，数据来源于Kaggle网站的Bank-Marketing数据集[17]。在实验中将22,900 条训练数据分为100个数据集，模拟100个数据拥有者，每个数据拥有者可以随机分配到299条数据，用于模拟出售数据，则根据式（3）计算出每个数据集的数据纯度如图2 所示。其中差分隐私通过添加噪声实现，隐私敏感分数随机取值为(0,1)，模拟数据拥有者的不同隐私需求。

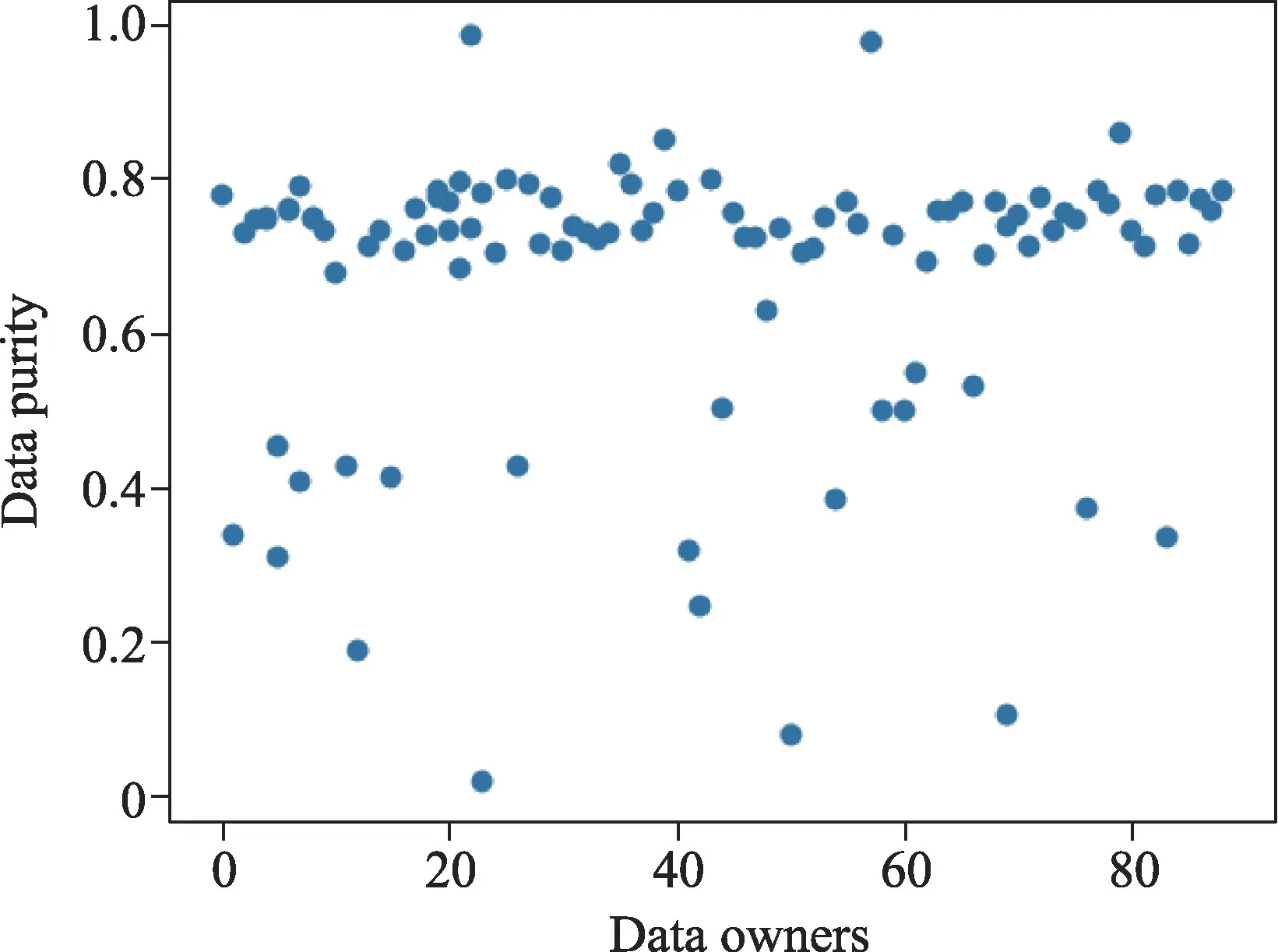
图2 100个数据集的数据纯度分布Fig.2 Data purity distribution for 100 datasets

4.2 实验结果与分析

4.2.1 补偿函数

首先，根据式（2）对100 个数据拥有者出售数据集的数据纯度进行打分，并用该数据训练模型，找出数据纯度与数据模型能达到的最大精度之间的关系，如图3所示。

图3 数据纯度和模型最大精度关系Fig.3 Relationship of data purity and accuracy

通过图3 可以看出，随着数据纯度的提升，模型能达到的最大精度也会随之提升，同时，数据纯度的提升达到一定值之后，对模型精度提升的影响便不再明显，即模型精度增长速率变缓。因此数据纯度可以作为模型定价基础。

4.2.2 数据平台收益

图4 展示了在给定补偿价格Po为数据平台在经过市场调查后，该模型在精度最高时可以卖出的价格的情况下，单位精度的购买价格Pc、精度acc和数据平台收益的关系。在实验中，假设成本函数α和β值从[0.1, 0.5]和[0.1, 1]中随机取出，模拟数据平台对模型训练成本不同的取值。从图中可以看出，当模型购买者要购买的模型精度不变的情况下，单位精度收购价格越高，数据平台收益越高。当单位精度收购价格不变的情况下，随着模型精度的增加，数据平台收益逐渐减少。

图4 数据平台收益Fig.4 Profits of the data platform

4.2.3 数据平台收益

图5展示了在单位精度的购买价格Pc、精度acc和模型购买者收益的关系。在实验中假设模型购买者收益函数参数σ从[1，+∞]随机取值，描述不同模型购买者对模型收益能力的不同理解。通过计算发现，当收益参数取值为1,000 时能够达到理想实验效果。由函数图像可以看出，当精度为最高，单位精度定价为最低的情况下，模型购买者取得收益最大值。当精度固定，收益随单位精度定价降低而升高。当单位精度定价固定，其收益随精度增加先升高后降低，符合凸函数特性。

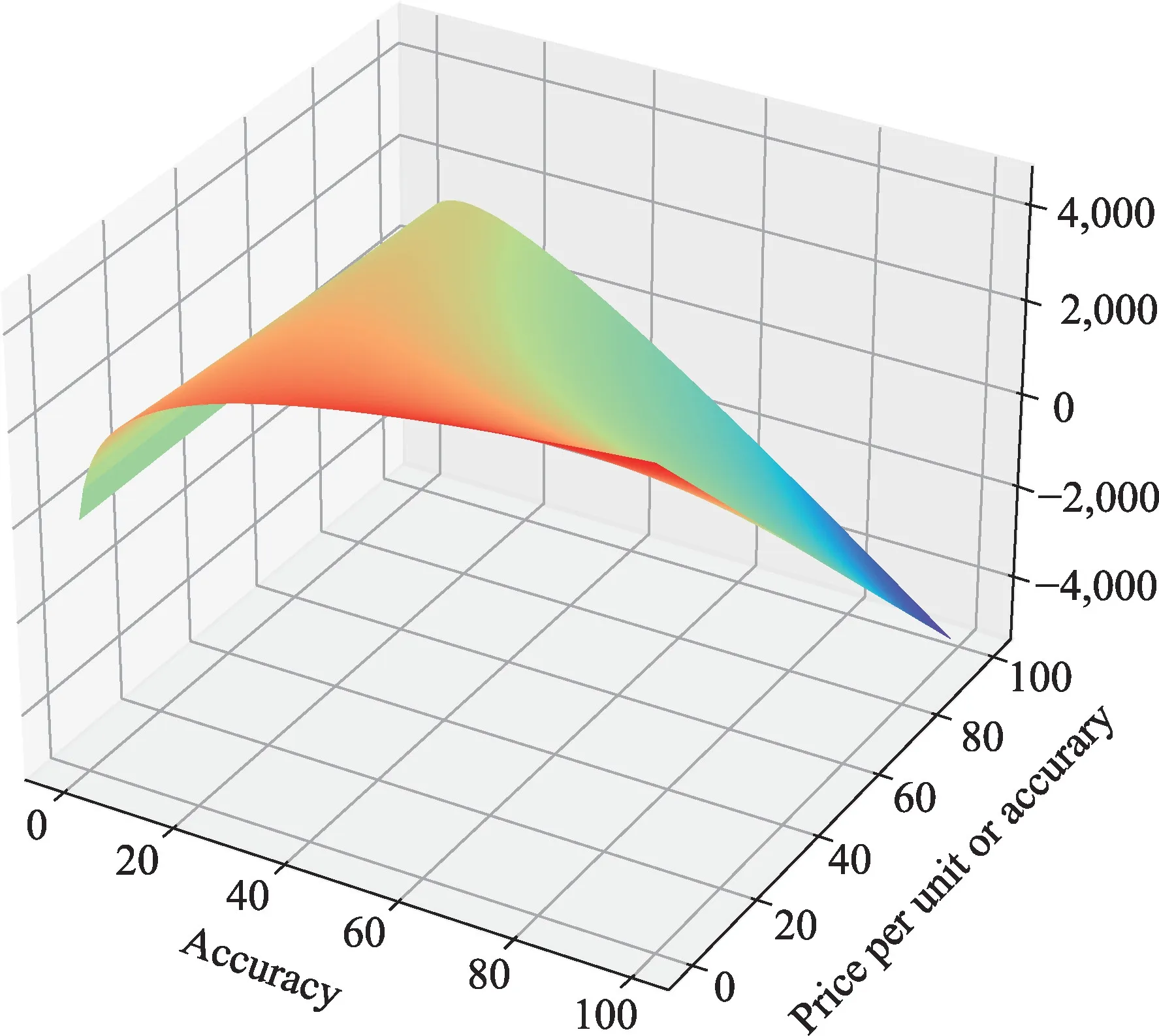
图5 模型购买者收益Fig.5 Profits of the model buyers

5 相关工作

随着物联网等技术的发展，数据无时无刻不在各行各业被收集，各种来源的数据汇集在一起形成的体量巨大、可以创造巨额商业价值的数据被称为大数据。但是仅有极少数的组织或个人拥有挖掘出大数据所有价值的能力，同时由于数据大量在生产侧聚集，不仅造成了数据资源的浪费，还给数据拥有者造成了巨大存储压力。因此，在数据定价的基础上模型定价与交易，成为让数据充分发挥价值的重要方法。

数据质量也是确定大数据价值的一个重要属性。早在20 世纪初，Wang 等人[18]对数据质量特征进行了两阶段的分类研究，制定了相关的分层框架，将数据质量特征分为了15 个维度。在数据定价方面，Yu等人[19]研究了在垄断平台下基于多数据质量维度的定价问题。该平台依据数据质量的多个维度，并且将不同维度之间的相互作用也考虑在内，设计了版本控制策略，建立了一个两层的编程模型以获得最终的定价。Yang等人[20]在总结了数据质量的不同衡量维度之后，选取了精准度、完整度和冗余度作为衡量数据质量的方式，允许依据上述3种维度对数据进行连续的版本划分，以产生不同质量水平的数据。提出了基于质量水平的效用函数，并从经济学角度考虑消费者支付意愿函数，共同计算出某个质量水平数据的出售价格。

随着大数据分析技术的发展，个人数据也成为数据市场中炙手可热的资源，其中包含的个人隐私可以对模型实用性产生影响，因此通常作为衡量数据价格的指标。Ghosh等人[21]首先提出了个人隐私数据交易，基于差分隐私给卖家提供隐私补偿。但其问题在于其差分隐私的ε值不支持用户自定义，缺少个性化定制功能，不能体现出数据拥有者对于隐私保护水平的差异。Zhang等人[22]针对上述缺点，提出了可以保证卖家个性化隐私需求的定价机制。同样采用差分隐私衡量隐私损失，确保数据拥有者自定义的差分隐私参数能够得到满足，并使用了反向拍卖机制决定购买哪个卖家的数据以及应该支付多少隐私补偿。本文采取类似思路，在满足数据拥有者隐私要求的前提下对数据进行处理，以尽可能获得数据的最大价值。

对于现在已经存在有关研究模型定价的文章，Jia 等人[5]专门为kNN 模型设计了定价机制。采用沙普利值法来衡量每个数据点对模型的贡献度，以此为依据对其进行定价。Song等人[23]在联邦学习的环境下提出了新颖的基于沙普利值的贡献指数，以衡量数据拥有者对于联邦学习模型的贡献。其提出了两种基于梯度的方法，第一种方法通过在不同轮次的梯度更新联合学习中的初始全局模型来重建模型，通过重建模型的性能计算贡献。第二种方法是通过更新前一轮的全局模型和本轮的梯度来计算每一轮的贡献指数。这两种方法能以高精度近似出贡献指数，并且极大提高了计算效率；缺点是只注重数据平台和数据拥有者的交互。Chen 等人[4]提出了基于模型的定价理论，卖家直接出售训练好的机器学习模型实例，而不是训练数据，使用模型精准度的不同来划分不同价格水平。提出的一种模型买家近似收益最大化的算法来解决成交价格问题；缺点是仅仅关注了模型买家一方的收益。本文则以数据质量和隐私为基础，提出了数据纯度的概念，以数据纯度作为数据拥有者公平补偿的基础。并且证明了数据纯度与模型精度的相关性。同时在模型出售端使用博弈论的方法使得数据平台和模型买家都能够达到收益最大化。

6 总结

本文提出了基于数据纯度的模型博弈定价方法，首先，在数据收集端，基于所收集到训练数据的质量和添加噪声数据多少两个指标提出了数据纯度的概念，并以其为依据对数据单位贡献进行补偿。其次，在数据出售端，数据平台根据模型购买者的购买意愿，以收集到数据为基础，训练出符合模型购买者需求和数据贡献者隐私保护程度的产品，以平台收购数据的成本即补偿金额和模型训练成本为其定价基础，与模型购买者进行两阶段的Stackelberg博弈，以使得双方都能够达到收入最大化。

利益冲突声明

所有作者声明不存在利益冲突关系。