改进人工蜂鸟算法的无线传感器网络部署优化

张 超，杨 忆

（1.宿州职业技术学院 计算机信息系，安徽 宿州 234101；2.淮北师范大学 计算机科学与技术学院，安徽 淮北 235000）

0 引言

无线传感器网络（wireless sensor network，WSN）是由静止或移动的无线传感器组成的分布式节点网络。WSN 具有多种类型的传感器，能够有效采集、处理和传输监测区域内各种现象，如温度、气压、噪声、土壤成分等［1］。目前，WSN 已被广泛应用于环境监测、智能医疗、智慧农业、军事等领域［2］。对监测区域的有效覆盖是影响WSN 监测质量的重要指标，在大型WSN 部署时，往往通过随机抛洒大量传感器节点以满足覆盖要求。但随机抛洒的部署方式容易造成覆盖盲区和大量的节点冗余，从而影响网络可靠性，且造成大量传感器资源浪费，增加了网络部署成本［3］。因此，研究WSN 部署优化，以便实现最大的监测覆盖和连通性，进而提升网络服务质量和节约部署成本，对WSN 部署来说具有重要现实意义。

元启发式算法因其随机性和对问题的黑箱处理，已经成为解决现实世界复杂优化问题的重要方法［4］。近年，用元启发式算法解决WSN 部署优化问题得到广泛关注。徐钦帅等［5］引入3 种策略改进蚁狮算法求解WSN 部署优化，覆盖率较基本蚁狮算法有明显提升，但与其他智能算法相比优势不明显。何庆等［6］引入双曲正弦、动态余弦波、拉普拉斯和高斯分布等算子改进正弦余弦算法，在求解WSN 部署优化问题时具有良好效果。宋婷婷等［3］通过引入量子位Bloch 球面和莱维飞行等方法提出一种改进的鲸鱼优化算法，与基本鲸鱼优化算法相比，改进的算法覆盖率得到提升，但要实现近似完全覆盖仍有待研究。王振东等［7］提出一种增强型麻雀搜索算法求解WSN 部署优化问题，在20 m × 20 m 监测场景中取得了较好效果，但在其他监测场景中的覆盖率还有待提高。上述算法在求解WSN 部署优化上是行之有效的，但如果要进一步提升WSN 的网络性能和应用效率，覆盖率和节点分布的均匀性仍需提高。

人工蜂鸟算法（artificial hummingbird algorithm，AHA）是Zhao 等［8］模拟自然界中蜂鸟的特殊飞行技能和智能觅食策略仿生设计的新元启发式算法。一般元启发式算法通常包含多个参数，而AHA 除了具有元启发式算法通用的种群规模和最大迭代次数外，只有一个迁徙觅食控制参数，有效降低了解决不同应用问题时参数难以确定的缺陷。但AHA 亦存在一般元启发式算法共有的缺陷，即在求解高维度、多峰值复杂优化问题时，易陷入局部极小值，导致算法收敛停滞。

综上，为进一步提升AHA 解决WSN 部署优化的覆盖率和节点分布的均匀性，本文提出一种改进的人工蜂鸟算法（improved artificial hummingbird algorithm，IAHA）。IAHA 使用两种改进策略：①添加基于蜂鸟个体和当代最优蜂鸟之间距离正切函数变换引导的候选觅食策略；②把使用柯西分布扰动的最优蜂鸟位置赋予最差蜂鸟，取代原迁徙觅食策略中随机赋值的位置更新方法。

本研究在12 个基准函数上验证了IAHA 的寻优性能，结果表明，IAHA 在收敛精度和速度上优于对比的算法。并选择文献中使用较多的4 种监测场景，做WSN 部署优化仿真实验，证实IAHA 的覆盖率高于相关文献中的算法。

1 WSN 节点覆盖模型

根据无线传感器网络的类型，可以用不同的方式定义最大覆盖问题。文献［3］和文献［9］中使用了两种常见最大覆盖率计算模型。本研究对两种覆盖模型进行了对比，在监测区域大小和传感器分布相同的情况下，两种方法计算的覆盖率一样，但文献［9］的方法在耗费的时间上大幅少于文献［3］中的计算方法。为了提高IAHA 实际应用的效率，本文采用文献［9］中的覆盖模型。并做如下假设：①每个传感器节点是均匀的，通信半径Rc是感知半径r的两倍；②在传感器节点通信半径范围内，每个节点可以实时感知并获取其他节点的位置；③传感器节点具有自由移动能力。

假设监测区域是二维平面，并将其数字化为m×n个像素点，每个像素点大小为1。在平面上随机抛洒N个传感器，节点集合为S={s1,s2,…,sN}，其中，节点i的坐标为si={xi,yi}。第i个传感器与目标像素点tp（x，y）之间的欧式距离为

本文使用二元感知模型，传感器节点i对目标像素点tp的感知概率为

一旦监测区域的像素点被任何一个传感器节点覆盖，该像素点的覆盖率取1。所有传感器节点的区域覆盖率Pcov为

WSN 覆盖优化的目标是使用最少的传感器达到最大的覆盖率。将（3）式作为目标函数，使用改进的人工蜂鸟算法找到一组传感器节点组合使覆盖率最高。

2 人工蜂鸟算法（AHA）

蜂鸟是世界上最小的鸟，拥有高超的飞行技巧和记忆力。AHA 通过模拟蜂鸟的特殊飞行技能和智能觅食策略仿生设计。AHA 模拟了蜂鸟的轴向、对角和全向飞行技能，并设计了一种访问表来实现蜂鸟寻找和选择食物来源的非凡记忆功能。AHA 假设食物源是解向量，食物源的花蜜填充率由函数适应度值表示。AHA 的迭代搜索主要由引导觅食、区域觅食和迁徙觅食3 个阶段构成。

2.1 引导觅食

在引导觅食阶段，假定n个蜂鸟被放置在n个食物源上。AHA 首先通过访问表为蜂鸟确定具有最高访问级别的食物来源，然后从中选择具有最高花蜜填充率的来源作为其目标食物来源。食物源的访问表由（4）式初始化，

式中，对于i=j，VTi，j=null 表示蜂鸟在其特定食物来源处进食；对于i≠j，VTi，j=0 表示在当前迭代中第i只蜂鸟刚刚访问了第j个食物源。算法执行中访问表的更新详情可参阅文献［8］。

蜂鸟选择候选食物源由（5）式计算，

式中，vi(t+1)表示候选食物源位置；xi(t)表示第i个食物源在时间t的位置；xi，tar表示第i只蜂鸟打算访问的目标食物源的位置；a为引导因子，服从正态分布N（0，1），均值为0，标准差为1。D表示模拟蜂鸟的轴向飞行、对角飞行和全向飞行3 种飞行技巧，使蜂鸟可以通过不同的飞行模式进行引导觅食。

轴向飞行由（6）式定义，

对角飞行由（7）式定义，

全向飞行由（8）式定义,

式（6）～式（8）中，d表示维度；randi（［1，d］）生成一个从1 到d的随机整数；randperm（k）创建一个从1 到k的随机整数排列；r1是（0，1）中的一个随机数。

蜂鸟在引导觅食阶段的位置更新由式（9）计算，

式中，f(•)表示函数适应度值。如果候选食物源的花蜜填充率优于当前食物源，蜂鸟将到候选食物源进食，否则停留在当前食物源进食。

2.2 区域觅食

模拟蜂鸟区域觅食策略的局部搜索的数学方程为

式中，b是一个地域因子，服从正态分布N（0，1），均值为0，标准差为1。

（10）式允许任何蜂鸟使用特殊飞行技能，但是在其当前位置附近寻找新的食物来源，仍使用式（9）进行区域觅食位置更新。

2.3 迁徙觅食

蜂鸟从花蜜补给率最差的来源迁移到随机产生的新来源的觅食过程由式（11）计算，

式中，xwor是种群中花蜜补充率最差的食物来源；r∈(0,1)是随机数；Up和Low是搜索空间上下界限。

3 改进人工蜂鸟算法（IAHA）

对AHA 的原理进行深入分析后发现，在算法的整个迭代搜索过程中，没有有效使用每代最优蜂鸟信息。而最优蜂鸟代表着到当前为止的最优解，其附近区域往往是最有希望获得全局最优解的地方。为此，本文通过两种策略将最优蜂鸟信息融入AHA 中，以进一步提高其处理高维度、多峰值复杂优化问题时的能力。

3.1 融入正切变换距离引导的候选觅食策略

在区域觅食阶段后，添加一个新觅食策略。新觅食策略首先计算蜂鸟个体和当代最优蜂鸟之间的距离，并对该距离实施正切函数变换。然后，让蜂鸟个体以最优蜂鸟位置为基准，以变换距离为飞行尺度寻找新的候选食物源。新觅食策略使用（12）式计算，

式中，xlbest（t）是第t代最优蜂鸟位置；tan（α）是正切函数，α∈（0，0.5π）是随机数，tan（α）的取值范围在（0，∞）之间；⊗是点乘符号；Dist是蜂鸟个体和当代最优蜂鸟之间的距离，由（13）式计算；sign（rand-0.5）是符号函数，值等于1 或-1，控制搜索的方向。

式中，rand是（0，1）中服从均匀分布的随机数。

新觅食策略在执行完式（12）后，执行式（9）进行贪婪选择。

3.2 柯西扰动变异的迁徙觅食改进

AHA 迁徙觅食原理是在整个搜索空间范围内，随机对最差蜂鸟位置进行重新赋值。该机制虽能拓展勘探空间，但因其盲目性也易造成收敛下降。因此，仍借助最优蜂鸟信息对最差蜂鸟进行引导进化。但同时为了防止种群过于集中在最优蜂鸟附近而造成种群多样性缺失，采用柯西分布对最优蜂鸟信息进行扰动。改进后的迁徙觅食位置更新用（14）式计算，

式中，r2为缩放因子，使用式（15）计算。cauchy为由均匀分布的随机数生成的柯西分布，使用柯西分布的逆累积分布函数计算，

式中，t为当前迭代次数；MaxIt为最大迭代次数。r2的值随迭代次数增加，从2 到0 指数递减。

式中，使用标准柯西分布，即x0=0，γ=1；R为（0，1）内服从均匀分布的随机数。

（16）式经过200 次迭代生成的柯西分布情况如图1 所示。从图1 可见，柯西分布整体分布稳定，但会间隔产生较大值。本研究用此特性防止种群长时间集中在当代最优蜂鸟附近区域，而失去探索其他有希望的区域，实现在迁徙觅食阶段局部开发与全局探索之间的转换，由此提升算法性能。

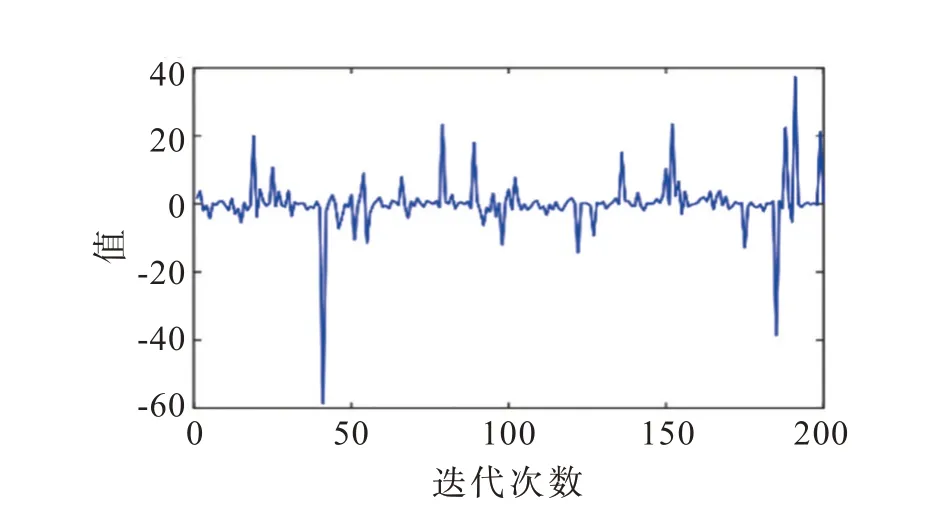
图1 200 次迭代后生成的柯西分布Fig.1 Cauchy distribution generated after 200 iterations

4 基于IAHA 的WSN 部署优化步骤

一个蜂鸟的个体编码对应一个传感器节点部署方案。假设一个蜂鸟个体编码为（x1，x2，…，xd），其中，（xi，xi+1）（i=1，2，…，d-1）代表一个传感器在二维平面上的位置。则基于IAHA 的WSN 部署优化步骤如下：

步骤1：输入监测区域范围、节点数v、感知半径r、蜂鸟种群规模npop、最大迭代次数MaxIt、迁徙觅食控制系数M=（npop/2）。

步骤2：随机初始化蜂鸟初始种群和访问表。

步骤3：使用（3）式计算初始蜂鸟种群的适应度即覆盖率，确定最优蜂鸟及其位置。

步骤4：使用（5）式进行引导觅食，执行（9）式并更新访问表。

步骤5：使用（10）式进行区域觅食，执行（9）式并更新访问表。

步骤6：使用（12）式进行正切变换距离引导的候选觅食，执行（9）式进行贪婪选择。

步骤7：使用（14）式进行迁徙觅食，并更新访问表。

步骤8：更新最优蜂鸟及其位置。

步骤9：重复执行步骤3～ 8，直至达到停止条件。

步骤10：输出最优蜂鸟及位置，即达到最高覆盖率的传感器节点部署方案。

5 仿真实验与分析

5.1 在基准函数上的性能分析实验

5.1.1 性能分析实验设计 选择12 个基准函数验证IAHA 的寻优性能。12 个基准函数见表1，维度均为30。为了充分验证IAHA 的性能，除了与基本AHA 对比外，选择近年效果较好的5 种算法进行对比实验。5 种算法分别是：人工生态系统优化算法［10］（artificial ecosystem-based optimization，AEO），鹈鹕优化算法［11］（pelican optimization algorithm，POA），海洋捕食者算法［12］（marine predators algorithm，MPA），鲸鱼优化算法［13］（whale optimization algorithm，WOA）和人工兔子优化算法［14］（artificial rabbits optimization，ARO）。所有算法种群规模统一设为30，最大迭代次数设为500，独立进行30 次实验。为确保对比算法获得最好性能，对比算法参数均采用相关文献推荐的设置。

表1 基准函数Tab.1 Benchmark functions

5.1.2 实验结果与分析 7 种算法在12 个基准函数上的对比实验结果见表2。由表2 可知，除f8外，IAHA 在两个评价指标上的结果均好于对比算法。在f8函数上，IAHA、AHA、AEO 和ARO性能相当，均好于POA、MPA 和WOA。在收敛到理论最优值方面，IAHA 在f1、f2、f3、f4、f9和f10上，30 次实验都能找到函数的理论最优值0，而其他算法均不能。f5、f6、f7、f11和f12函数较复杂，因此一般元启发式算法很难获得它们的理论最优值。但实验结果表明，IAHA 的寻优精度明显优于对比算法，且整体提高几个数量级。从标准差指标看，IAHA 具有稳健的鲁棒性。从而说明本文提出的改进策略是有效的。

5.1.3 算法收敛性分析 限于篇幅，选择7 种算法在部分函数上的收敛曲线进行对比，结果见图2。由图2 可知，IAHA 的收敛速度明显快于对比算法。特别在f1、f3和f9上，IAHA 在第220 代左右就已经收敛到函数的最优值，说明正切变换距离引导的候选觅食策略和柯西扰动变异的迁徙觅食改进策略，有效提升了算法的收敛速度和收敛精度。

5.2 基于IAHA 的WSN 部署优化仿真实验

5.2.1 仿真实验设计 本文选择文献中使用较多的4 种WSN 部署场景进行WSN 部署优化仿真实验，考查IAHA 在WSN 部署优化方面的性能。将WSN 参数与对比文献设置的一样，IAHA 的种群规模设置为30，最大迭代次数设置为1 000，实验结果取30 次部署优化的平均值。

5.2.2 20m×20m监测区域部署优化 在该区域随机抛洒24 个同构传感器，感知半径r=2.5 m。将监测区离散化为20 × 20 个像素点。实验结果表明，IAHA 的平均覆盖率最高（见表3）。IAHA 比随机抛洒、AHA、ESSA、ESCA、IWOA、MS-ALO 和DACQPSO 分别提升23.51%、0.77%、0.84%、2.29%、3.44%、3.63%和9.84%。经反复实验，IAHA 使用22 个传感器覆盖率可达到94.81%，比ESCA、IWOA 和MS-ALO 可节省2 个传感器；IAHA 使用19 个传感器覆盖率即可达到88.58%，比DACQPSO 可节省5 个传感器。图3 为随机抛洒、AHA 和IAHA（使用24与22 个传感器节点）的部署分布对比图。从图3（a）可得，随机抛洒方式部署的传感器出现大量重叠和覆盖盲区，严重影响WSN 的网络性能。图3（c）相较于图3（b），明显提高了覆盖效果，说明IAHA 提升了AHA 的性能。图3（d）说明IAHA 在使用22 个传感器的情况下，亦有较好的覆盖效果。

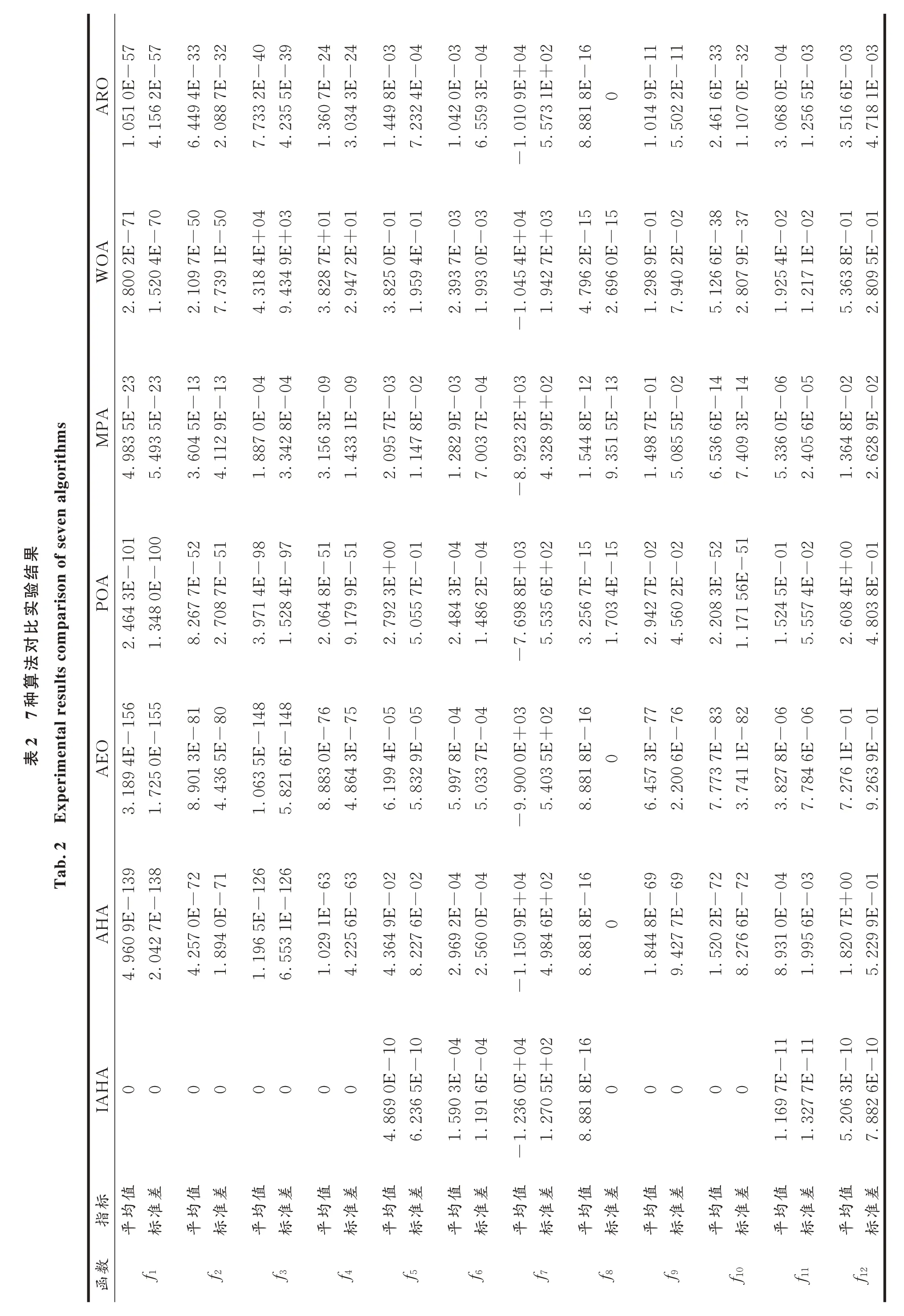
表3 20 m × 20 m 监测区域平均覆盖率结果比较Tab.3 Comparison of average coverage rate results of 20 m × 20 m monitoring area deployment

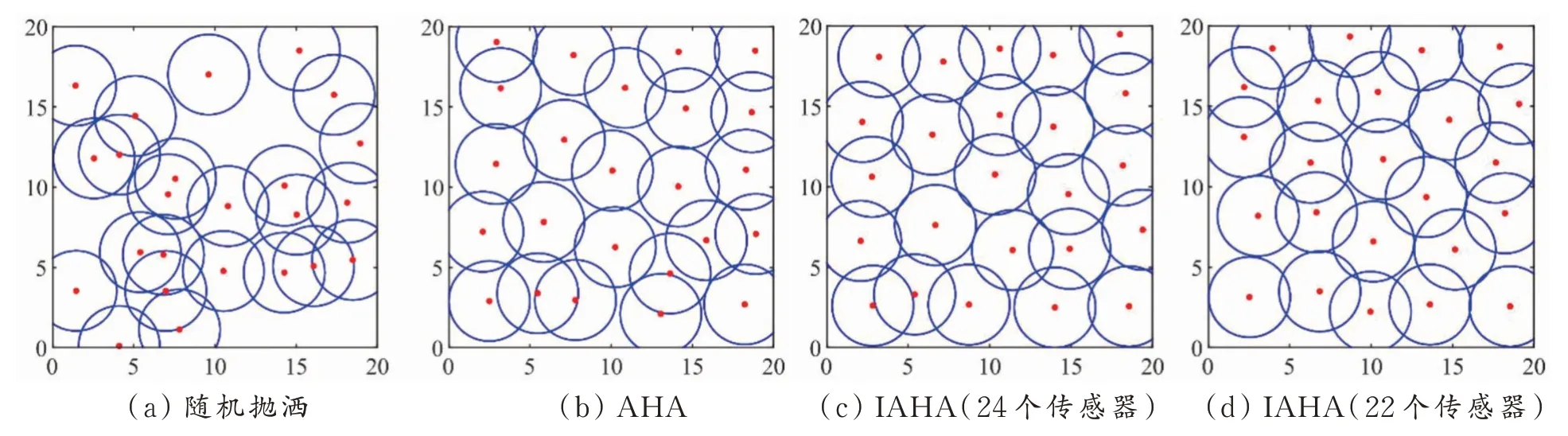
图3 20 m × 20 m 监测区域部署优化对比图Fig.3 Optimization comparison diagram of 20 m × 20 m monitoring area deployment

5.2.3 30 m × 30 m 监测区域部署优化 在该区域随机抛洒20 个同构传感器，感知半径r=5 m。将监测区离散化为31 × 31 个像素点。实验结果表明，IAHA 实现近似全覆盖（见表4），在平均值和最差值上都高于对比算法。IAHA 平均值分别比随机抛洒、AHA、ESCA 和VFPSO 提升14.36%、0.08%、0.32%和1.96%。经反复实验，IAHA 使用19 个传感器覆盖率可达99.89%，与AHA 使用20 个传感器相当；IAHA 使用18 个传感器覆盖率可达到99.81%，比ESCA 可节省2 个传感器；使用16 个传感器覆盖率即可达98.82%，比VFPSO 可节省4 个传感器，节约成本。图4为随机抛洒、AHA 和IAHA（使用20 和16 个传感器）的部署对比图。从图4（a）、图4（b）和图4（c）可得，IAHA 的部署漏洞较随机抛洒和AHA 减少，分布更均匀。由图4（d）可得，在减少传感器的情况下，IAHA 优化的网络覆盖良好，分布均匀。

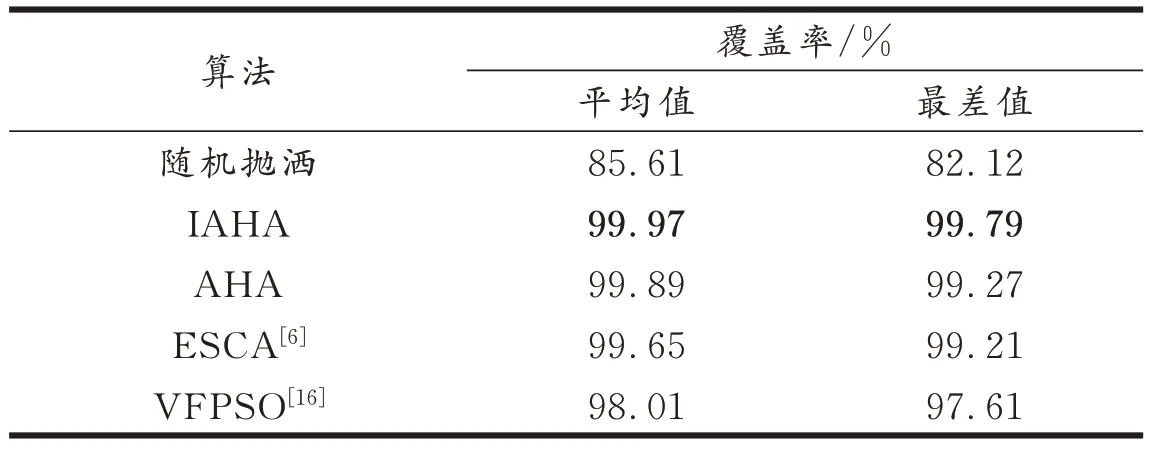
表4 30 m×30 m 监测区域覆盖率结果比较Tab.4 Comparison of coverage rate results of 30 m × 30 m monitoring area deployment

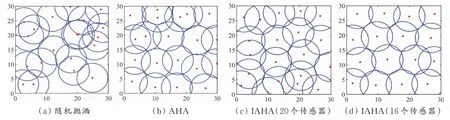
图4 30 m×30 m 监测区域部署优化对比图Fig.4 Optimization comparison diagram of 30 m × 30 m monitoring area deployment

5.2.4 50 m × 50 m 监测区域部署优化 在该区域随机抛洒35 个同构传感器，感知半径r=5 m。将监测区离散化为50 × 50 个像素点。实验结果表明，IAHA 分别比随机抛洒、AHA、ESSA 和DACQPSO 提升25.06%、1.07%、0.92%和10.52%（见表5）。经反复实验，IAHA 使用34 个传感器覆盖率可达93.56%，与AHA 和ESSA 使用35 个传感器部署的实验结果基本相当；IAHA 使用28 个传感器覆盖率即可达到84.61%，比DACQPSO 更可节省7 个传感器。图5 为随机抛洒、AHA 和IAHA（使用35 和28 个传感器）的部署对比图。从图5 可得，35 个传感器时，IAHA 覆盖良好，分布均匀，能有效提升网络的性能，在IAHA 使用28 个传感器时仍有不错的部署效果。

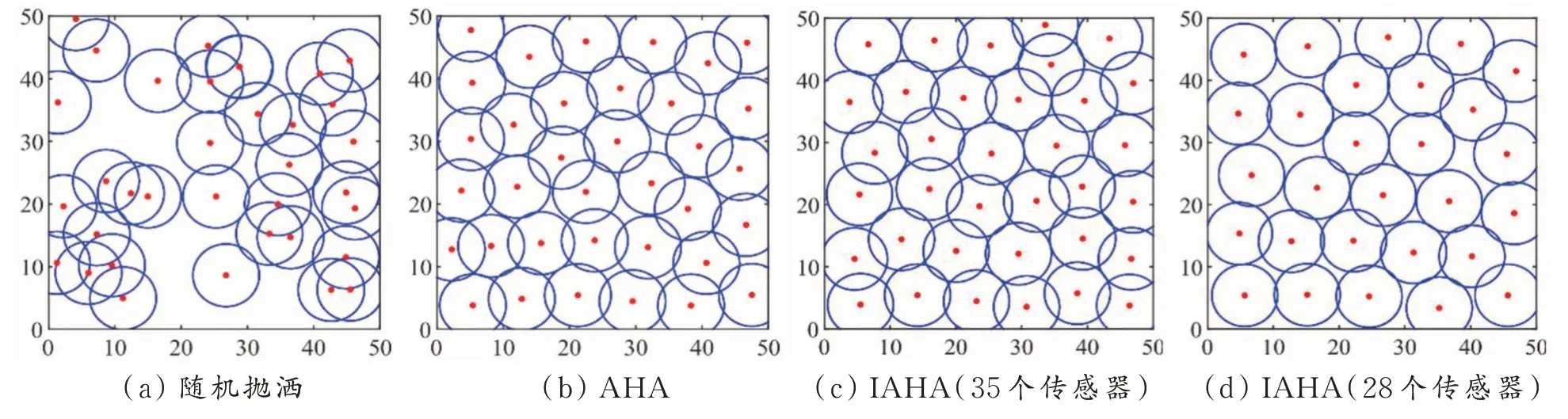
图5 50 m × 50 m 监测区域部署优化对比图Fig.5 Optimization comparison diagram of 50 m × 50 m monitoring area deployment

5.2.5 100 m × 100 m 监测区域部署优化 在该区域分别做50 个和40 个传感器部署优化实验，传感器感知半径r=10 m。将监测区离散化为101 × 101 个像素点。表6 为50 个和40 个传感器部署实验结果，表中IWOA 算法50 个节点结果来自文献［3］，40 个节点来自本实验，其他算法结果均来自相关文献报道的结果，表中“—”表示对比算法没有相关实验。

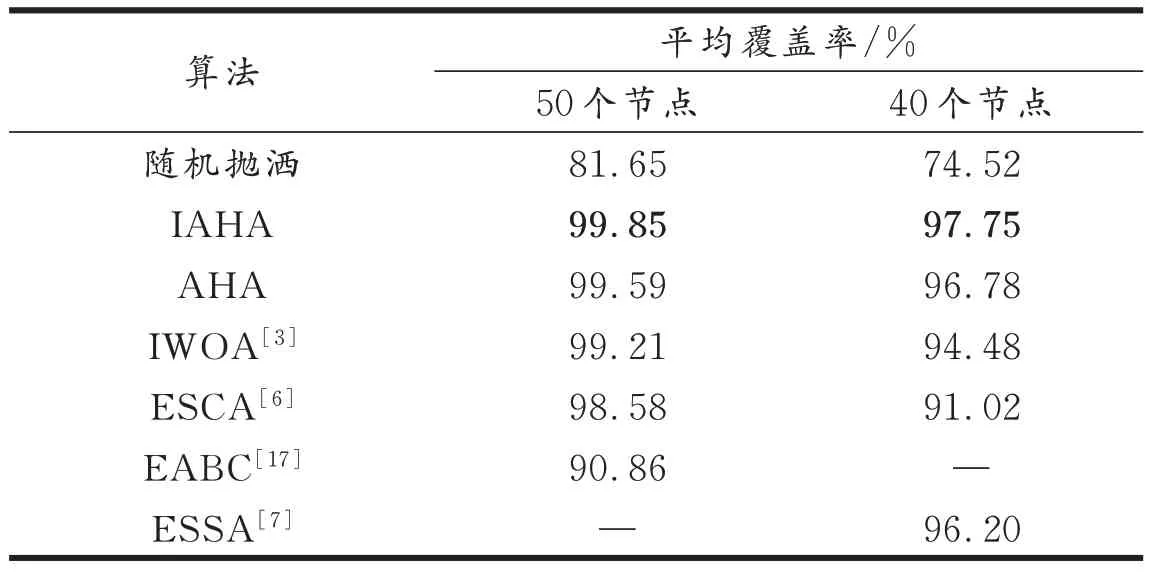
表6 100 m×100 m 监测区域平均覆盖率结果比较Tab.6 Comparison of average coverage rate results of 100 m × 100 m monitoring area deployment

从表6 可见，IAHA 在50 个和40 个传感器部署实验中获得的覆盖率都高于对比算法。在50 个节点时，AHA、IWOA 和ESCA 均有良好的优化效果，但当传感器节点减少到40 个时，IAHA 的覆盖率明显高于它们。经反复实验，IAHA 使用33 个传感器覆盖率即可达到91.13%，较ESCA可节省7 个传感器，较EABC 可节省17 个传感器，大幅节约成本。

图6 为随机抛洒、AHA 和IAHA 的部署优化对比图。从图6 可见，IAHA 在50 个节点时近似全覆盖，在40 个节点时较AHA 减少了覆盖空洞。

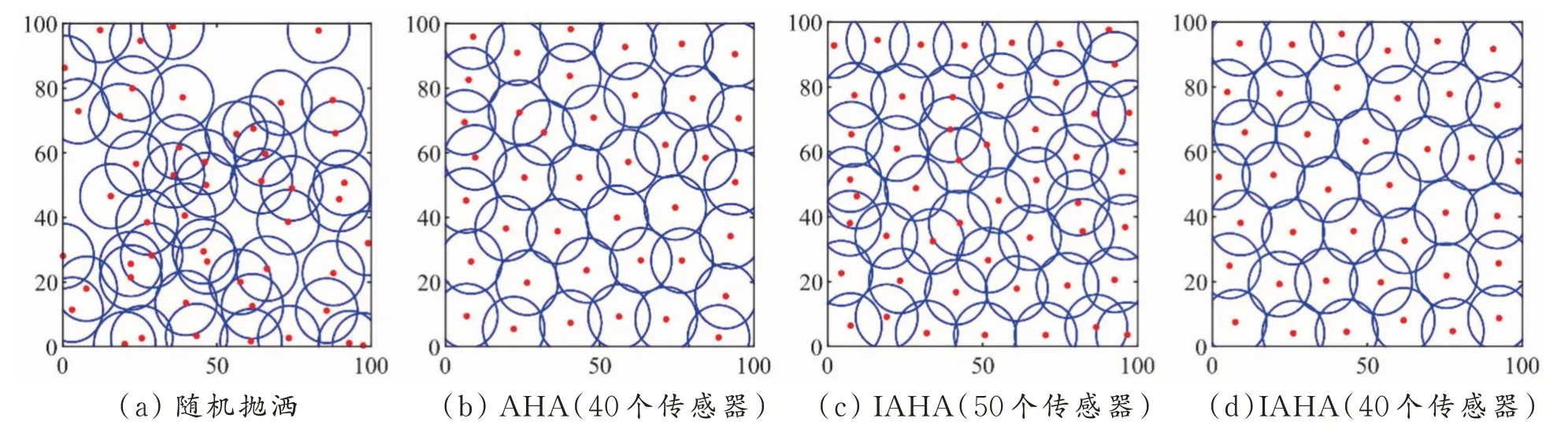
图6 100 m×100 m 监测区域部署优化对比图Fig.6 Optimization comparison diagram of 100 m × 100 m monitoring area deployment

综上仿真实验结果与近年文献报道中表现较好的算法比较，IAHA 在平均覆盖率上高于这些算法，且在大幅减少传感器节点的情况下，覆盖率仍高于部分算法，且节点分布均匀。从而说明，本文提出的IAHA 算法在融入正切变换距离引导的候选觅食策略和柯西扰动变异的迁徙觅食改进后，适合求解WSN 部署优化，应用效果较好。

6 结语

鉴于人工蜂鸟算法在求解高维度、多峰值复杂优化问题时易陷入局部极小值，导致算法收敛停滞，本文提出一种改进的人工蜂鸟算法（IAHA），并应用其优化无线传感器网络部署。IAHA使用正切变换距离引导的候选觅食策略和柯西扰动变异的迁徙觅食改进策略，将最优蜂鸟信息融入算法迭代搜索过程，充分发挥最优个体对种群的引导作用。在仿真实验部分，首先在12 个基准函数上验证了IAHA 的寻优性能。实验结果表明，IAHA 在收敛精度和速度上优于AHA、AEO、POA、MPA、WOA 和ARO 等新兴算法。其次，在4 种监测区域上进行了WSN 部署优化仿真实验，结果表明，IAHA 的平均覆盖率高于对比算法，且传感器节点分布均匀，在大幅减少传感器的情况下，仍具有良好的覆盖率和均匀度。IAHA 提升了基本AHA 的性能，适合求解WSN 部署优化问题，未来将进一步研究IAHA 在其他工程优化问题中的应用。