基于Tracker的非光滑下滑轨道的最速降线研究

魏王杰

(云南师范大学物理与电子信息学院 云南 昆明 650092;云县第二中学 云南 临沧 675800)

刘 垚

(云南师范大学体育学院 云南 昆明 650092)

姚 斌

(云南师范大学物理与电子信息学院 云南 昆明 650092)

1 引言

最速降线在逃生轨道、粮食输运轨道[1]、过山车轨道、滑板场地、以及我国古建筑中的“大屋顶”排水系统[2]中均有应用.

最速降线最初由伽利略提出,后经牛顿、洛必达、莱布尼茨等验证,在不考虑阻力时,它是一条下凹的圆摆线[3].然而,在真实的物体下滑过程中,下滑物体总会受到诸如摩擦力、粘滞力等的作用(其中摩擦力受正压力影响,正压力又受物体自重、速度和所处下滑轨道位置的影响;而粘滞力则受速度、温度等影响,因此,这些力都是大小、方向均在变化的非线性力),使得对真实下滑过程的研究变得异常复杂.

Tracker是一款视频分析和物理建模软件,利用它可以标记用户所指定的视频中的目标,从而进行位置追踪、旋转角度分析、动力学模型分析等操作[4].因此,可利用该软件辅助进行非光滑最速降线问题的研究.

本文在分析最速降线问题的基础上,设计制作非光滑下滑轨道实验装置,进行6个轨道的下滑实验;利用Tracker软件分析获取下滑实验中小球的位移时间曲线,进而对比研究6个非光滑下滑轨道的下滑时间,获得并验证其中下滑时间最短的下滑轨道曲线.

2 最速降线问题

无阻力时的最速降线问题可表述为:在一竖直平面内有不重合的两点P和M,M位于P的斜下方,在该竖直平面内的所有连接P和M的路径里,找出一条路径,使得质点在只受重力作用下,从P点开始静止下滑,到M点的滑行用时最短.

该问题最早由伽利略在1630年提出[5],后经众多学者分别利用常规数学变分法、斯涅尔定律等方法求解[6-8],得出一致结论:无阻力时的最速降线是一条下凹的圆摆线,其解的形式为

(1)

其中,C为常数,α为引入的参量.

然而,在实际的下滑过程中,物体不仅受重力作用,而且还受其他阻力——如摩擦力等的影响,于是,最速降线将不再是圆摆线.不过,经文献[8]证明可知,当只考虑摩擦力时,最速降线中任意一点的切线方向与水平方向的夹角(记为β)对时间的导数应为常数,即β-t图像应是一条直线.在后文中,我们也将把这个因素作为判别是否是最速降线的一个标准.

3 实验装置设计及实验过程

3.1 实验装置设计

为了利用Tracker软件研究从P点到M点的最速降线问题,本文设计了如图1所示的最速降线实验装置.该装置由底座、起点挡板、终点挡板、雪弗板轨道、背景板、激光笔校准装置、校准条以及直径为10 mm的红色小玻璃球构成.其中,起点挡板高45 cm,终点挡板高5 cm,两板水平距离60 cm,P点和M点水平相距60 cm,竖直相距40 cm.此外,制作雪弗板轨道的雪弗板长度、宽度和厚度分别为90 cm、30 cm、0.3 cm,以保证其有足够的延展性可以弯成不同的轨道,且足以承载小玻璃球对轨道的压力,从而在小球滚下时轨道不发生明显弯曲,进而影响实验结果.同时,为了使小球的运动轨迹在竖直平面上,沿着弯曲雪弗板轨道表面还粘贴了彼此平行的两条间距为10 mm的雪弗板细条.

图1 最速降线实验装置

实验还设置了激光笔校准装置.实验时打开激光笔开关,调整其位置使小球在点P位置时激光均射在小球球心,以确保小球每次都能从点P开始运动,从而减小实验误差.此外,实验装置中还有长0.4 m的校准条,作为在Tracker软件中建立标尺时的参照物.另外,本实验之所以选择白色背板和红色小球,是为了提高小球和背景的对比度,便于利用Tracker软件更准确的实时追踪小球,从而获得较为精确的小球运动轨迹.

3.2 实验过程

(1)6个下滑轨道的获得

(2)小球的自由下滑

参看图1,从轨道上端P点无初速度释放小球,使其沿雪弗板轨道自由下滑到M点.释放小球前已先打开激光笔校准装置,使小球每次释放时激光都正射过小球的球心,以确保每次小球都从相同的位置释放.

(3)视频录制

利用静止放置的手机以录像的形式记录下小球在各轨道上的运动过程.为了能利用Tracker软件准确抓取小球的运动过程,手机视频录制时设置视频的分辨率为1080 P,帧率60帧,视频编码的兼容性设置为最好,并在良好的光照条件下进行视频录制.

4 数据提取及分析

4.1 利用Tracker软件提取数据

实验视频处理过程如图2所示,详细步骤为:

(1)如图2(a)所示,找到所录制的小球下滑视频;

(2)导入视频:如图2(b)所示,打开Tracker软件,将实验视频慢放0.5倍处理并导入;

(3)建立坐标系:如图2(c)所示,用“十”字定位针选取起点挡板的顶部为坐标原点,使坐标的横轴正向与底座平行并指向右,纵轴正向建立在竖直面内竖直向上.

(4)建立标尺:如图2(d)所示,选择底板上的白色雪弗板校准条为参照物,并输入参照物的长度为0.4 m;

(5)建立质点:如图2(e)所示,将小球中心设为质点;

(6)追踪质点:如图2(f)所示,逐帧分析小球运动的视频,找到小球从P点运动到M点的起始帧和结束帧,可获得小球的运动时间、位置坐标和速度等物理量.

4.2 实验数据分析

(1)小球运动的6个轨迹

将Tracker中小球运动的水平位移x和竖直位移y全精度导入Origin,可得小球在轨道1～6上的运动轨迹,分别如图3(a)～(f)所示.

图3 小球在6个轨道上的运动轨迹

(2)小球的运动时间

小球在6个轨道上的运动时间均少于1 s,用手动计时方法难以准确记录.实验中采用逐帧追踪的方法,利用Tracker追踪小球在每一帧的运动时间,再利用总帧数计算出小球运动的总时间.为了进一步提高时间精度,导入Tracker中时把视频进行了慢放0.5倍处理,使每帧对应的时间减少了一倍,即把时间精度提高了一倍.

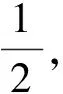
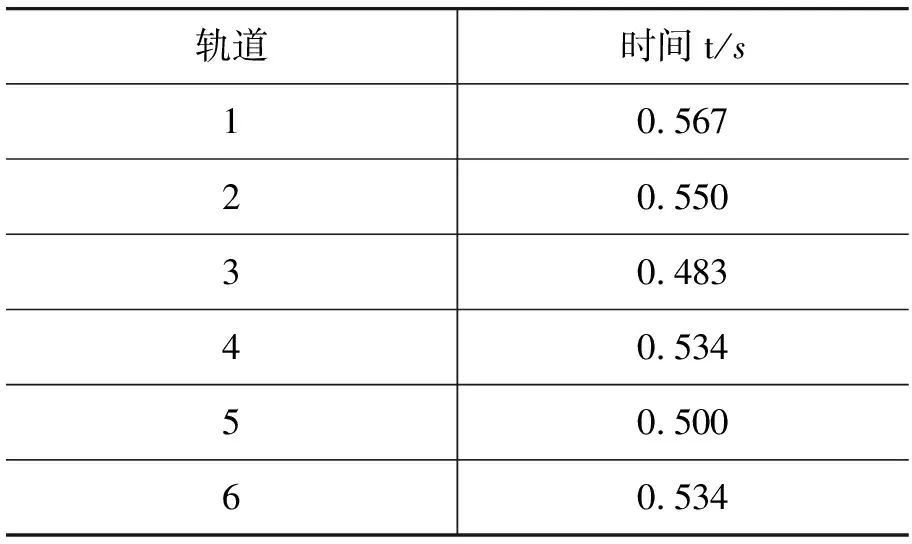
表1 各轨道上的小球下滑总时间

图4 轨道3的小球运动数据

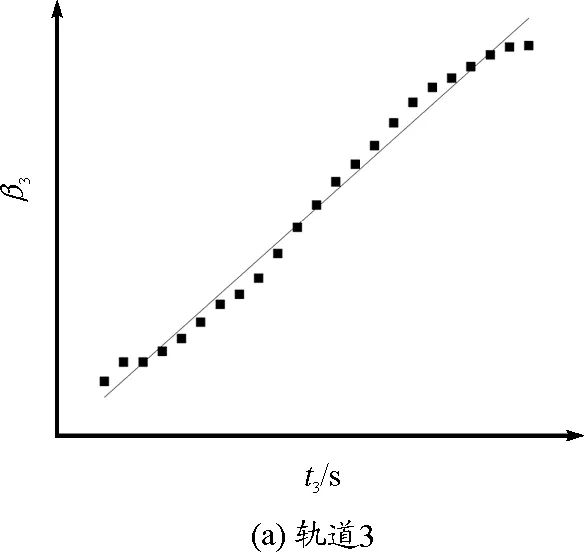
图5 轨道3和5的小球β-t线性拟合图

(3)小球运动最速下降轨道的寻找

6个轨道的下滑时间如表1所示.由此可得,小球在轨道3和5上的运动总时间都出现了极小值,因此,我们还需考虑这两条轨道的轨迹斜率是否具有匀变性,即在最速降线轨道上运动的物体其轨道切线方向与x轴的夹角β随时间是均匀变化的,也就是β-t图像应该满足线性关系(是一条直线).利用Origin软件绘出轨道3和5上小球运动的β-t散点图,并进行线性拟合,如图6所示.经计算,轨道3的线性拟合度为0.986 34,而轨道5的线性拟合度仅为0.941 79.因此,轨道3更趋近于最速降线.

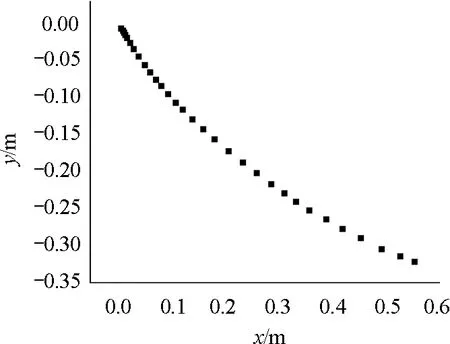
图6 圆摆线轨道上的小球运动轨迹

(4)最速降线轨道与圆摆线轨道的比较

将M点的位置坐标(0.6,-0.4)代入圆摆线方程(1),可解出C=0.2,α=3.07,取α∈[0,3.07]作出此摆线,并将雪弗板轨道弯成该摆线的形状,进而进行小球下滑实验.同样,利用Tracker分析小球的下滑视频,可得小球的运动轨迹如图6所示,下滑的总时间为0.517 s,比轨道3的更长.可见,对于非光滑轨道,圆摆线并不是最速降线,这也和现存文献的结论是一致的.

4.3 误差分析

在利用Tracker软件进行实验数据提取过程中,最主要的误差可能出现在把小球近似为质点所引起的误差.这个误差来源于两方面,一方面是运动方式的不同(小球做的是滚动,包含一部分角动能,而质点的运动则不包含角动能),一方面是运动路径识别的时候,小球的球心高于实际轨道,也会引入一定的误差.

为此,本文还利用Matlab编程求解了光滑轨道时的最速下滑时间为0.438 s,和非光滑轨道的最速下滑时间0.483 s(表1)比较,我们的求解误差应远小于10%,应用在教学甚至研究中都较为可靠.

5 结论

本文利用Tracker软件辅助进行非光滑下滑轨道最速降线问题的研究.在分析最速降线问题的基础上,制作了非光滑下滑轨道实验装置,进行了6个轨道的下滑实验,进而利用运动轨迹分析软件Tracker从下滑视频中分析获得下滑过程的位移时间曲线.研究结果表明,利用Tracker软件辅助,可以分析原本难以分析的复杂运动学问题,为物理教学提供了便利.