基于位移矢量三角形的抛体运动射程问题探析

黄 伟

(湖北汉川一中 湖北 孝感 431600)

1 问题的提出及缘由

抛体运动的形式及应用很多,其中有一类关于射程的特殊问题,以一定速率沿水平面斜上抛、沿斜面向上抛、沿斜面向下抛(忽略空气阻力,重力加速度为g).

问题1：当射程最远时,抛射方向需要满足什么条件?

问题2：当射程一定时,最小速度的抛射方向需要满足什么条件?

问题3：当射程相等时,两次抛射方向需要满足什么条件?

问题4：当射程最远时,初速度方向与末速度方向有什么关系,有没有一定的规律呢?

伽利略在1638 年出版的《关于两门新科学的对话》这部著作中,有了惯性思想和对自由落体运动的研究,进一步研究了抛体运动,伽利略认为抛体运动具有匀速运动和自然加速运动的复合运动的性质.

在中学阶段一般采用正交分解法分析抛体运动,对于斜面上的斜抛运动,若涉及复杂的三角函数,采用正交分解法在两个方向上多次分解往往会让问题变得比较复杂.而把抛体运动分解为沿初速度方向的匀速直线运动和竖直方向的自由落体运动,建立位移矢量三角形,利用正弦定理来求解,可以得到简单的表达式,无需多次分解,这也正是回到了伽利略对抛体运动研究的思想,下面笔者具体展开分析.

2 问题分析

2.1 以沿斜面向上抛为例

2.1.1 数学分析

如图1所示,小球从倾角为α的斜面上的O点向上抛,落于P点,初速度v与斜面的夹角为θ.小球从O到P的运动,可分解为沿初速度v方向的匀速直线运动和竖直方向的自由落体运动,如图2所示建立位移矢量三角形.

图1 沿斜面向上抛情境图

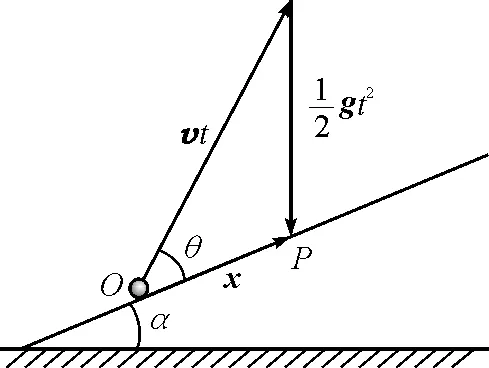
图2 位移矢量三角形

由正弦定理可得

(1)

取前一个等号化简得

(2)

将式(2)代入式(1)得

(3)

由三角函数积化和差得

(4)

(5)

2.1.2 得出结论

(6)

(2)由式(5)可知,当射程x一定时,抛射方向为竖直向上方向与位移方向之间的角平分线时,速度最小

(7)

(3)由式(4)可得,x相等时有两个解θ1和θ2,满足

2θ1+α+2θ2+α=π

(8)

(9)

如图3所示,OO1为竖直向上方向和位移方向夹角的角平分线.

图3 关于角平分线对称抛

当两个抛射角满足θ1+θ2=∠MOP时,则

∠MOB=∠AOP=θ1∠BOO1=∠O1OA

即OO1也为两个抛射方向的夹角∠BOA的角平分线,即两个抛射方向关于竖直向上方向与位移方向之间的角平分线OO1对称时,射程相等.

(4)如图4所示,在上述图2的分析基础上,小球从倾角为α的斜面上由O点以初速度v抛至P点,沿初速度方向与竖直方向建立位移矢量三角形OAP.同理,由运动的反演,在P点以vP将小球反向抛出,则落于O点,同样沿初速度方向与竖直方向建立位移矢量三角形PBO,由于BO与AP平行且相等,则四边形ABOP为平行四边形.当抛射方向为竖直向上方向与位移方向之间的角平分线时,此时平行四边形ABOP为菱形,即抛出速度v与落点速度vP方向垂直,由上述本节的第(1)个小问题的分析可知,抛射方向为竖直向上方向与位移方向之间的角平分线时,射程最远,可得:当射程最远时,初速度方向与末速度方向垂直.

图4 初速度方向与末速度方向垂直

2.2 类推至沿水平面斜上抛和沿斜面向下抛

如图5和图6所示,OP2为水平面,即α=0,设倾斜面OP1的倾角α1为正值,则倾斜面OP3的倾角α3为负值,满足对应相同的位移矢量三角形关系.

图5 沿不同面的最远射程图

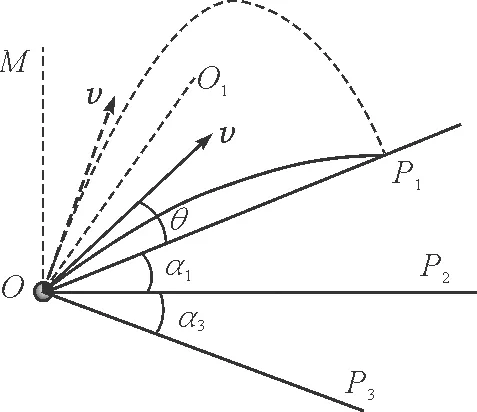
图6 沿不同面的等射程图

同理可得到:

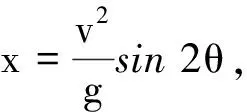
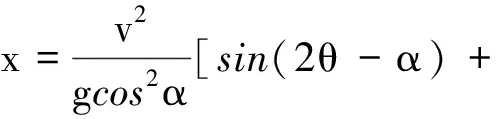
当射程x一定时,抛射方向均为“竖直向上方向与位移方向之间的角平分线”时,速度最小.同理可知,两个抛射方向关于竖直向上方向与位移方向之间的角平分线OO1对称时,射程相等,且射程最远时,初速度方向与末速度方向垂直.

2.3 利用几何画板模拟验证

以下是在几何画板中取重力加速度为g=10 m/s2,初速度v=4 m/s,抛射方向与x轴正方向成5°～85°每间隔5°所得到的17条抛物线组合图像.由图7可知,当两个抛射方向关于角平分线45°线方向对称时射程相等,且沿角平分线45°线方向抛出至水平面射程最远.

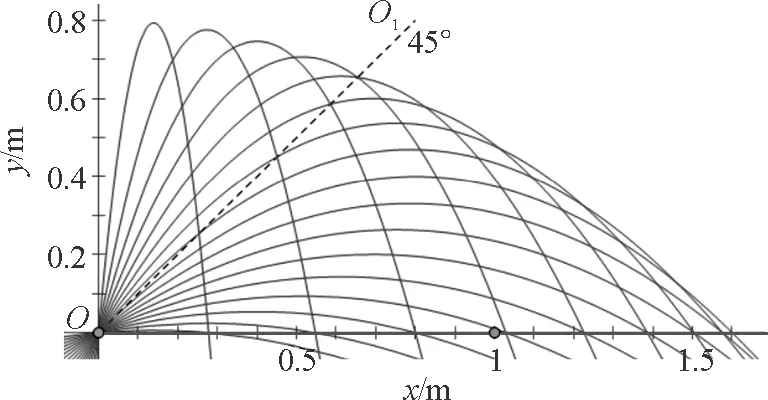
图7 沿水平面斜上抛抛物线族

由图8可知,当两个抛射方向关于角平分线60°线方向对称时射程相等,且沿角平分线60°线方向抛出至倾角为30°的斜面上射程最远.

图8 沿斜面向上抛抛物线族

由图9可知,当两个抛射方向关于角平分线40°线方向对称时射程相等,且沿角平分线40°线方向抛出至与水平面成10°向下的斜面上射程最远,具体射程也可以根据理论计算值与实际模拟值对比.

图9 沿斜面向下抛抛物线族

3 得出结论

综上可得,无论沿水平面斜上抛,还是沿斜面向上抛、向下抛,均满足:

(3)当两个抛射方向关于“竖直向上方向与位移方向之间的角平分线”对称时,射程相等.

(4)当射程最远时,初速度方向与末速度方向垂直.

4 结束语

还有很多其他的运动学问题也可以通过建立位移矢量三角形或速度矢量三角形求解,这里只是以抛体运动中一类特殊规律的位移矢量三角形探析为例.矢量三角形在运动学中有着广泛的应用,正弦定理及三角函数的运用,进一步体现了高考物理能力要求中的应用数学处理物理问题的能力.