不同轴压比下纤维增强水泥基复合材料加固砌体墙抗震性能数值模拟研究

2023-11-08刘代智李媛李晓琴

新型建筑材料 2023年10期

刘代智，李媛，李晓琴

（昆明理工大学建筑工程学院，云南昆明 650500）

0 引言

砌体结构作为我国既有建筑的主要结构形式之一，在城市工业与民用建筑中有着举足轻重的地位[1]。砌体结构的基本力学特点是抗压强度高，抗拉、抗剪强度低，导致砌体结构的整体性和抗震性能不佳[2]。汶川地震后，我国土木专家小组对各类建筑物的震害进行了现场调查，调查结果显示，砌体结构房屋是所有建筑物中抗震能力最弱、破坏程度最大的结构之一[3]。

纤维增强水泥基复合材料（ECC）是一种兼具高韧性、高抗渗性的新型材料，其力学性能优异，受力时，纤维在裂隙中的桥联作用使得纤维与基体间在应力传递时裂缝能够稳定扩展，使ECC 表现出明显的多缝开裂特性和应变硬化行为，可有效抑制裂缝的产生与扩展，广泛应用于结构的抗裂、防水、抗震、耐久性修复等领域[4]。周铁钢等[5]使用ECC 对空斗墙体加固，探究十字型条带加固和双面满抹加固对空斗墙抗震性能的影响，结果表明，十字型条带加固能延缓裂缝地开展的同时提高墙体的耗能能力，双面满抹加固能较好地提高墙体的整体性。Soleimani-Dashtaki 等[6]使用延展性水泥基复合材料（EDCC）对无筋砌体墙单面加固，对加固后的全尺寸砌体墙进行振动台试验，结果表明，加固后墙体整体的延展性和耗能能力得到了明显提升，大幅提高了墙体在倒塌前的整体漂移极限。

现有ECC 加固砌体墙研究多是在相同轴压比下进行抗震性能试验，但在实际的砌体结构中不同楼层砌体墙的轴压比是随着楼层降低而逐渐增加的。因此进行在不同轴压比下模拟ECC 加固砌体墙的抗震性能试验对比研究具有重要意义。本文通过对砌体墙模型进行可靠性验证，对0.1、0.3、0.5轴压比下的未加固砌体墙和ECC 加固砌体墙进行模型设置，并施加模拟地震作用的边界条件，对模拟结果的破坏模态、滞回曲线、骨架曲线和累积耗能进行对比分析，研究了不同轴压比对ECC 加固砌体墙抗震性能的影响。

1 砌体墙模型可靠性验证

1.1 模拟原型

选取王卓琳等[7]的未加固砌体墙试件为模拟原型，试件由加载梁、砖砌体墙和底梁3 部分组成，加载梁和底梁由钢筋混凝土浇筑而成，砖砌体墙高1750 mm、宽2115 mm、厚240 mm，采用一顺一丁方式砌筑，模拟原型如图1 所示，各材料的力学参数如表1 所示。

表1 材料的力学参数

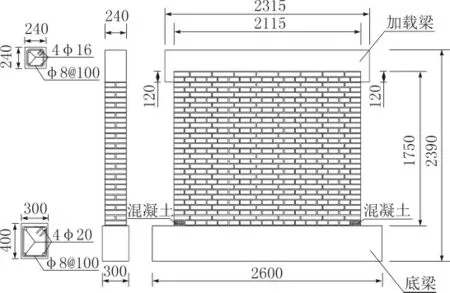
图1 模拟原型

1.2 数值计算模型

Abaqus 软件中常见的砌体墙建模方式有3 种，分别为整体式建模、精细化建模与简化式精细化建模[8]。整体式建模将砖砌体墙当成均质材料，把砂浆离散在整个墙体中，这种模拟方式较为粗糙，但能大幅缩减计算成本；精细化建模是将砂浆与砌块分别建模，同时通过界面接触模拟砂浆与砌块之间的粘结作用，这种模拟方式最为精确，但计算成本极高，且模型不易收敛；简化式精细化建模是不对砂浆进行直接建模，而是通过零厚度的接触属性来定义砂浆的粘结作用，这种模拟方式得到的结果较整体式建模更加精确，计算成本较精细化建模低。综合考虑模拟精度和计算成本，本文采用简化式精细化建模方法对砌体墙建模。

对砖块使用塑性损伤模型（CDP）进行模拟，此方法适用于单调荷载、循环荷载及动态荷载作用下材料的数值分析。参照刘海平等[9]的砖块拉压本构参数，采用能量法定义损伤因子d，能够较好地模拟砖块在循环荷载下的力学性能及损伤扩散的现象，砖块拉压本构参数如表2 所示。

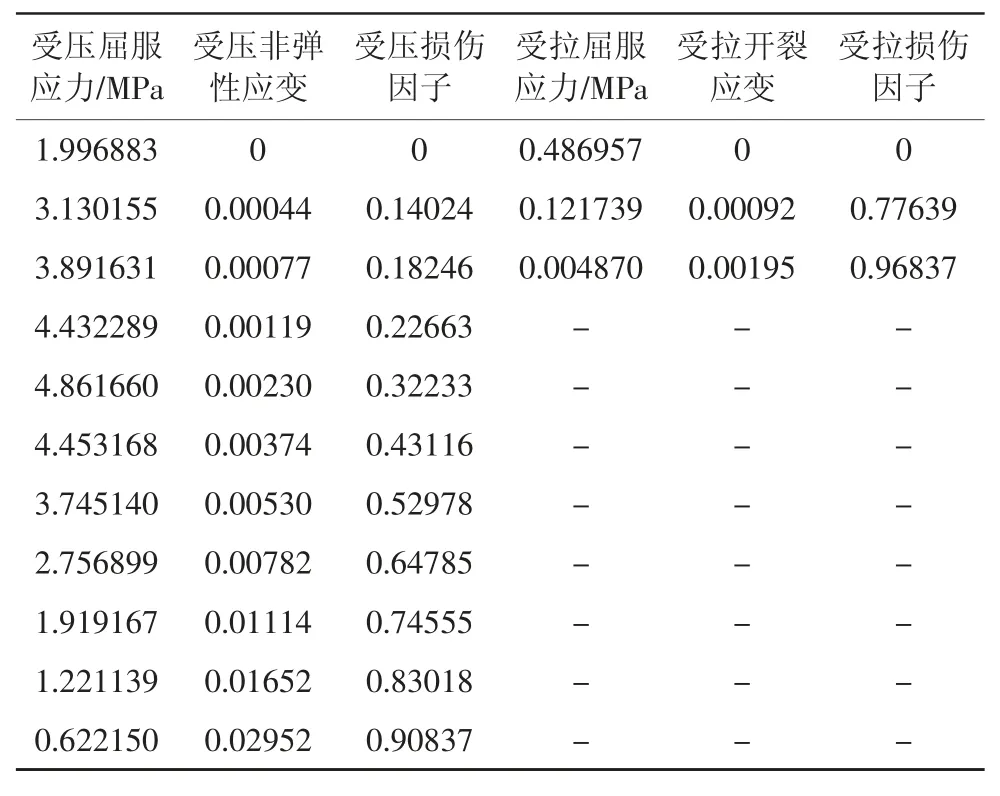
表2 砖块拉压本构参数

砖块塑性参数设置为：膨胀角ψ 为38°，偏心率e 为0.1，双轴与单轴受压时的初始屈服应力比fb0/fc0为1.16，不变应力比k为0.66667，粘性参数v为0.005。由于钢筋混凝土加载梁和底梁的刚度和强度远远大于砌体墙，在试验过程中仅用于加载，不作为主要研究对象，所以将加载梁和底梁简化为线弹性材料，设置其弹性模量为32 500 MPa，泊松比为0.17。

使用双线性本构模型模拟砖块的连接界面在法向拉力和切向剪力下的牵引分离现象，这种本构模型包括材料达到强度极限前的线弹性阶段和材料达到强度极限后刚度线性下降的软化阶段。Quade Damage 选择二次名义应力准则，使用摩擦原理定义砖块之间发生脱胶后的接触属性，法向设置“硬”接触，切向采用库伦摩擦模型，其摩擦系数设置为0.75。界面接触参数如表3 所示。

表3 界面接触参数

对砖块进行划分网格，网格全局尺寸设置为50 mm。划分加载梁和底梁网格时，由于加载梁和底梁不是模型分析的主要对象，所以使用较粗尺度的网格进行划分，网格全局尺寸设置为100 mm。砖块、加载梁和底梁采用八结点线性六面体C3D8R 单元。

1.3 模型验证

根据JGJ/T 101—2015《建筑抗震试验规程》中的拟静力加载方式对试件加载，得到模拟和试验的骨架曲线对比如图2 所示。

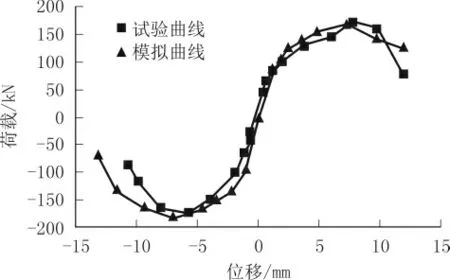
图2 骨架曲线对比

如图2 所示，随着正负位移的增加，两条骨架曲线荷载呈现先增大后减小的趋势，模拟曲线与试验曲线较为吻合；模拟曲线的正向峰值荷载为171.56 kN，试验曲线的正向峰值荷载为175.20 kN，误差为2%；模拟曲线的反向峰值荷载为182.32 kN，试验曲线的反向峰值荷载为176.1 0kN，误差为3.5%。

试验裂缝和模拟损伤云图如图3 所示。

图3 试验裂缝与模拟损伤云图对比

由图3 可见，随着循环位移的增加，墙体缓慢出现斜向裂缝，随后出现两条主斜裂缝交汇于墙体中部，最终出现沿墙体对角线方向的贯通斜向裂缝，模拟云图中墙体沿着对角线方向发生塑性损伤破坏。模拟与试验较为吻合，模型可靠。

2 ECC 加固砌体墙模型设置和边界条件设置

建立轴压比分别为0.1、0.3、0.5 的未加固砌体墙模型，分别命名为W-1、W-2、W-3；建立轴压比分别为0.1、0.3、0.5 的3片ECC 加固砌体墙模型，分别命名为EW-1、EW-2 和EW-3。

2.1 ECC 加固砌体墙模型设置

ECC 高延性、高韧性的特征，常用作墙体抗震加固材料。Meng 等[10]将ECC 的受拉过程分为弹性阶段、多缝开裂阶段和应变硬化阶段。Feenstra 等[11]用断裂能表示ECC 的受压过程，并用抛物线的形式表示受压曲线。

Meng 等[10]的ECC 受拉本构计算方程，如式（1）所示：

式中：σt——ECC 的受拉应力，MPa；

ε——ECC 在受拉应力状态下的应变；

σt0——初裂时的拉应力，MPa；

εt0——初裂时对应的应变；

σtp——极限拉应力，MPa；

εtp——极限拉应力时对应的应变；

εtu——极限拉应变。

Feenstra 等[11]的ECC 受压本构计算方程如下：

式中：σc——ECC 的受压应力，MPa；

Ec——ECC 的弹性模量，MPa；

ε——ECC 在受压应力状态下的应变；

fc——ECC 的抗压强度，MPa；

h——有限元模型单元特征长度为单元体积；

Gc——受压断裂能，N/mm。

设置ECC 模型尺寸为2040 mm×1590 mm×10 mm，赋予Meng 等[10]和Feenstra 等[11]的拉压本构和损伤参数，网格大小划分为30 mm×30 mm×10 mm。单面加固砌体墙，ECC 和砖块之间的界面属性定义为绑定接触。

2.2 边界条件设置

轴压比U计算方法如式（5）所示：

式中：N——砌体墙所受竖向荷载，kN；

A——砌体墙截面面积，mm2；

fC——砌体墙轴心抗压强度设计值，kN/mm2。

根据GB 50003—2011《砌体结构设计规范》，砂浆强度等级为M2.5、砖强度等级为MU20 的砌体墙抗压强度设计值为1.95 MPa，将其代入公式（5）计算得出向轴压比为0.1、0.3、0.5砌体墙施加的竖向荷载分别为95.47、286.41、477.36 kN。

底梁设置为固定约束，假设其不发生任何移动和转动。对加载梁施加水平往复位移模拟地震作用，参照JGJ/T 101—2015 的加载方式：最初每级往复循环位移依次增加0.5 mm，每级往复循环1 次，当墙体屈服时，每级往复循环位移依次增加2 mm，每级往复循环2 次，直至墙体所能承受的荷载下降到峰值荷载的85%，试件破坏，模拟结束。

3 模拟结果分析

3.1 塑性损伤云图分析

使用Abaqus 软件计算模型，得到W-1、W-2 和W-3 以及EW-1、EW-2 和EW-3 破坏后的塑性损伤云图分别如图4、图5 所示。

图4 未加固砌体墙塑性损伤云图

图5 ECC 加固砌体墙塑性损伤云图

由图4 可知：W-1、W-2、W-3 试件的破坏模态均呈现X型，且3 个试件的塑性损伤程度越来越大，“X”型破坏模态越来越明显。W-1 试件的损伤多停留于墙片左下角和右下角并呈现出受压破坏；W-2 试件的损伤沿着墙体对角线方向明显上移，墙体出现受压破坏和剪切破坏；W-3 试件的损伤沿着墙体对角线贯通，整个墙体损伤严重，墙体出现剪切破坏。未加固墙体随着轴压比的增大，墙体的受损程度越大。

由图5 可知：EW-1 的损伤主要从墙体下部向墙体中部扩散，抵抗墙体的受压变形；EW-2 的损伤从墙体中下部向上部扩散，抵抗墙体的受压变形和剪切变形；EW-3 的损伤从墙体中部向四个墙角扩散，抵抗墙体的剪切变形。3 个试件的损伤所占墙体的面积逐渐增加，说明随着轴压比的增大，ECC抵抗墙体变形的作用越明显。

3.2 滞回曲线和骨架曲线分析

滞回曲线和骨架曲线可以较好地反映墙体在循环荷载下的力学行为，各试件的滞回曲线如图6 所示，滞回曲线特征点模拟结果如表4 所示，骨架曲线如图7 所示。

表4 各试件滞回曲线特征点模拟结果

图6 滞回曲线

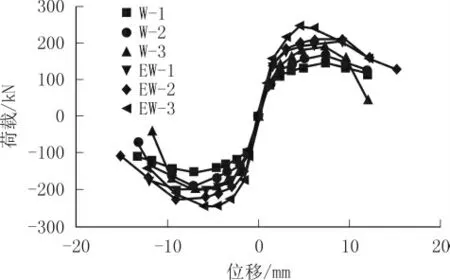
图7 骨架曲线

由图6、图7 和表4 经计算后可知，W-1，W-2、W-3 在循环荷载加载初期处于弹性阶段，卸载后刚度退化较小，塑性变形较小。随着加载位移的增加，W-1、W-2、W-3 先后屈服，其屈服荷载分别为115.42、130.93、147.43 kN。W-1 的峰值荷载为149.64 kN，W-2 的峰值荷载为179.94 kN，W-3 的峰值荷载为199.12 kN，W-2 的峰值荷载较W-1 提高了20.24%，W-3 的峰值荷载较W-2 提高了10.65%。未加固墙体在轴压比为0.1、0.3、0.5 下，墙体能承受的水平荷载依次增大，墙体的抗震性能依次增强。

EW-1、EW-2、EW-3 的滞回环较W-1、W-2、W-3 的滞回环均更饱满，屈服荷载和峰值承载力均有不同程度提高。EW-1 的屈服荷载较W-1 提高了26.47%，EW-2 的屈服荷载较W-2 提高了11.13%，EW-3 的屈服荷载较W-3 提高了13.01%，说明使用ECC 加固后的砌体墙，墙体抵抗变形的能力增强，在地震作用下墙体更不易出现裂缝。EW-1 的峰值荷载较W-1 提高了33.78%，EW-2 的峰值荷载较W-2 提高了26.45%，EW-3 的峰值荷载较W-3 提高了21.97%。EW-1、EW-2 和EW-3 到达峰值荷载后的下降段较W-1、W-2、W-3的下降段更平缓，这是由于ECC 断裂时纤维的桥联作用使砌体墙的延性增强。采用ECC 加固后的砌体墙承载能力和变形能力显著优于未加固砌体墙，ECC 加固后的砌体墙随着轴压比的增大，墙体的抗震性能增强。

3.3 累积耗能分析

滞回曲线中各个滞回环所包围的面积之和为墙体的累积耗能，累计耗能越多，抗震效果越好。各试件的累积耗能曲线如图8 所示。

图8 累积耗能曲线

由图8 可知：随着水平位移的增加，试件W-1、W-2、W-3累积耗能不断增加。在相同循环位移下，试件W-1、W-2、W-3的累积耗能依次增大，表明墙体轴压比为0.1、0.3、0.5 时，墙体的抗震性能依次增强。EW-1、EW-2、EW-3 的累积耗能分别为1366、、1550、、2026 kN·mm，累积耗能依次增大，说明地震作用下ECC 加固砌体墙的累积耗能随着轴压比增大而增加，抗震性能逐渐增强。EW-1 的累计耗能较W-1 提高114.1%，EW-2 的累计耗能较W-2 提高41.5%，EW-3 的累计耗能较W-3 提高39.3%，说明ECC 加固后的墙体较未加固墙体累积耗能更大，加固后的墙体抗震性能增强，当轴压比为0.5 时，ECC 加固后的墙体抗震性能最好。