油菜光谱的函数特征分析及叶绿素诊断建模

许 健

(湖南农业大学 信息与智能科学技术学院,湖南 长沙 410128)

0 引言

自20 世纪90 年代起,精确农业从概念走向实践并开始商业化运营,作物生长状况实时监测是精确农业众多技术环节中的重要一环.作物信息科学的重点内容是如何利用作物的信息对其进行无损营养诊断,光谱分析便是一个有效可行的途径.对于油菜而言,冠层光谱特征是描述其营养状况的重要指标.随着观测技术的进步,光谱分辨率不断提高,高光谱技术开始广泛用于作物营养状况实时监测.高光谱技术中的光谱分辨率大大提高,光谱波段之间存在很强的自相关现象[1,2].此时,光谱适宜于看成是一条连续的曲线,而曲线的形状变化特征则蕴含了作物信息.实际上,许多植被指数都可以看成是对某个特殊的光谱特征的描述,比如,比值植被指数、归一化植被指数、土壤调节植被指数等都重点利用了光谱中的红边特征信息.

基于叶片或冠层反射光谱的分析技术是最近几十年来广为流行的植物营养状况无损监测手段之一.绿色植物组织的各种色素以及细胞结构特点导致了其反射光谱中会呈现一些独特的形状特征,比如红边特征[3,4].大量研究证实了红边特征与植物的众多生理物理性质有着密切关系,比如叶面积指数、生物量、叶绿素密度等[5,6].从最初的比值型植被指数以及归一化植被指数开始,各种改进的光谱植被指数不断被构造出来以提取反射光谱中的信息,进而用于植物的生物物理性质研究[7～9].早期的地球资源卫星上搭载的是分辨率较低的多光谱传感器,随着传感器技术的进步,高光谱技术的应用逐渐普及,研究者已经意识到低分辨率的多光谱技术不足以准确探测植被的生物化学性质,波段宽度在10 nm 以下的高光谱则有着广阔的应用前景[9].但是,基于多光谱时代的植被指数构建方式,使用高光谱数据建模的效果不一定比使用多光谱数据的效果好[5].高光谱所携带的信息量显然要比多光谱大得多,出现这一困境说明高光谱分析方法还需要进一步开发.

针对高光谱数据,有许多研究工作延续了多光谱数据的思路,如首先挑选出少数几个最优波长,再对经典的基于多光谱的植被指数进行优化或另外构建新的指数[10～13].多光谱分析技术习惯于将各个波段当作相互独立的变量来对待,这样的假设在处理多光谱数据时是合适的,比如红光波段和近红外波段看起来很像是两个“相互独立”的信息源,叶绿素在红光波段和近红外波段的光吸收情况也确实存在显著的差异,但是类似的看法在处理高光谱数据时是不恰当的.高分辨率情况下,相邻的波长变量之间的“实体意义”很难区分清楚,光谱波长之间存在很强的自相关现象,哪个波长最优本身是有一定模糊性的.此时,光谱更应当看成是一条连续的曲线,而曲线的形状变化特征则反映了作物的信息[14].目前,已经有一些研究工作探讨了从连续曲线的视角来研究光谱数据[15,16].

函数型数据分析(Functional Data Analysis)方法于20 世纪80 年代开始在统计学领域提出.以光谱数据为例,该方法最大的特点是将整条光谱曲线看作一个整体,从函数角度研究光谱曲线的变化特征.通过各个波长的“离散”观测值恢复出背后的函数,即连续光谱曲线,进而从整体上研究曲线的典型变化特征,不再仅仅从最优的几个波长提取光谱信息.从函数的角度研究光谱特征拓宽了光谱信息提取的思路,如果选择最优波段构建光谱指数可以看成是一种“离散”的思路,那么基于函数的方法则代表一种“连续”的思路,避免了因高度相关导致的最优波段挑选的模糊性,以及由此造成的信息丢失.

1 理论与方法

1.1 函数型数据分析

用{(tj,yj),j=1,2,…,n}表示一条光谱观测记录,其中tj表示波长,yj为相应波段位置上的光谱观测值,n是光谱中所使用的波长个数.假设所观测到的离散光谱观测值实际上来自一条连续的光谱曲线,用函数x(t) 表示,则观测值与真实光谱函数的关系为

即在tj位置上观测到的光谱值yj实际上是由真实的光谱值x(tj)加上一个观测误差εj而得到.函数型数据分析方法首先要根据观测到的光谱估计出真实的光谱曲线函数x(t).一般的,一条光谱观测值就可以估计出一个函数,为了提高估计精度,也可以同时使用实验中在某个观测点上的若干重复光谱观测值来估计同一个函数.误差项εj的方差在所有波长tj上相同或不同,要根据实际情况决定,具体的估计方法参考文[17].

函数型主成分分析(Functional PCA)[18,19]是探索函数曲线典型变化特征的一个非常有用的方法.在函数型PCA 中,一个数据样本即为一个函数,计算出的主成分也是函数,画出来是一条曲线,表示的是在一组函数(即若干条曲线)中出现最多的曲线变化特征,因此函数型PCA 可以用来识别光谱或导数光谱中的典型变化特征.

1.2 增强回归树

增强回归树(Boosted Regression Trees,BRT)是Schapire[20]于2002 年提出的一种机器学习方法,它融合了两类算法——分类回归树与boosting,通过boosting 整合大量的分类回归树模型来改进单独一棵树的性能.与bagging 方法所使用的直接对大量普通模型取平均不同,boosting 是逐步序列式进行的,在建立下一棵树时会以更高的权重考虑在之前已经建立的树上表现不够好的那些样本,强调在这部分样本上改进预测性能,通过这种方式,boosting 不仅能够减小预测方差,还能减小预测偏差.有关细节参见文[21,22].

1.3 最大信息系数

最大信息系数(Maximal Information Coefficient,MIC)是由D.Reshef 等提出的一种用于测量两个随机变量之间相依关系的方法,Speed 将其称为21 世纪的相关系数[23].MIC 方法具备两个非常吸引人的特点:广义性(generality)和等价性(equitability).广义性指的是它能够度量变量之间可能存在的各种关系,而不仅仅局限于线性或者某几个明确的函数关系.而等价性指的是MIC 的取值大小只与变量之间的关系强度有关,不依赖于具体的关系类型,只要关系强度类似,MIC 取值大小就会差不多.MIC 的取值范围在0 到1之间,取值越靠近于1 说明两个变量之间的关系越密切,若MIC=0,则说明两个变量相互独立.

2 试验与数据

以湖南农业大学浏阳试验基地的48 个小区的中熟高油酸油菜为研究对象,48 个小区中24 个为移栽种植方式,另24 个为直播种植方式.选择晴朗、无风无云的三个日期: 2014 年12 月2 日(苗期),2015 年1月22 日(抽薹期),2015 年4 月16 日(荚果期),于每个日期的10:00 至13:00,利用美国ASD 公司(Analytical Spectral Device)生产的FieldSpec®3 高分辨便携式地物波谱仪进行采样.波谱仪的有效波段范围为350～2500 nm,其中,350～1000 nm范围采样间隔为1.4 nm,光谱分辨率为3nm;1000～2500 nm 范围采样间隔为2 nm,光谱分辨为10 nm.测量时距离冠层垂直高度约0.7m,采用标准白板校正,因此所采集光谱为无量纲的相对反射率.

48 个种植小区苗期、抽薹期和荚果期所采集的光谱如图1 所示.抽薹期光谱相较于苗期和荚果期,在波长大于1000 nm 的中红外区域,光谱反射峰明显低于苗期和荚果期.为了获取叶绿素含量信息,在每个种植小区选取长势平均的5 个植株的第三片展开叶,利用日本MINOLI.A 公司生产的SPAD 502 叶绿素仪,测定5 个点的叶片SPAD 值.具体来说,每个叶片从叶尖到叶枕分成3 段,在每段的二分之一处进行测定,各段重复5次,取平均值,作为该点位的叶片SPAD 值.如图2 所示,与冠层光谱情况类似,抽薹期的叶片SPAD 分布比其他两个生长期明显要高,平均值达到了55;苗期和荚果期相比,苗期的SPAD 值分布相对集中,而荚果期的则更加分散.

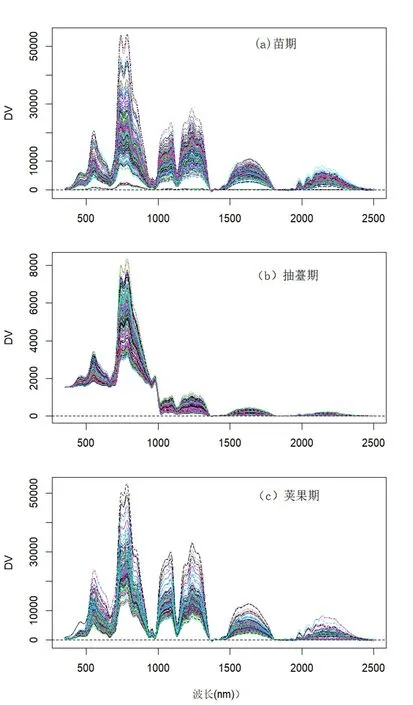
图1 48 个种植小区所采集的光谱

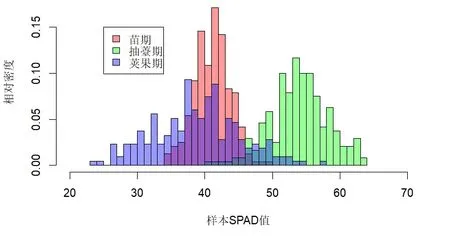
图2 苗期、抽薹期、荚果期叶片SPAD 测量值频数分布

3 结果与讨论

3.1 光谱特征与函数主成分

图3 为三个生长期数据的第一、第二主成分函数,其中第一主成分解释了数据中82.9%的波动信息,而第二主成分解释了5.1%的信息.图3中的实线是光谱平均值,而“+”和“-”表示的是给均值加上或减去一定量的主成分之后的效应.容易观察到,不同样本光谱间的差异主要在各反射峰区域出现,即“+”和“-”所标示的曲线分离得最开.比起第一主成分,第二主成分更加强调1500～2500 nm 范围内反射峰的差异信息.但是,如图4 所示,第一主成分得分值的大小与叶片SPAD 值之间无明显规律性,说明光谱在这些反射峰上的波动信息并不能直接用于叶绿素含量建模.偏最小二乘(PLS)方法是一种使用非常广泛的适用于解释变量远多于样本个数情况的线性建模方法.图5为5个主成分的PLS 模型的交互验证预测情况,5 个主成分解释了解释变量99.61%和响应变量68.63%的信息,交互验证均方根预测误差(RMSEP)为4.609,达到样本SPAD 平均值的10.3%.从图5 中容易看出,PLS 模型给出的预测值与样本测量值之间几乎没有呈现出线性关系.

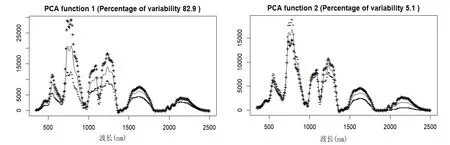
图3 第一主成分与第二主成分函数

图4 样本第一主成分得分值与样本SPAD 值散点图

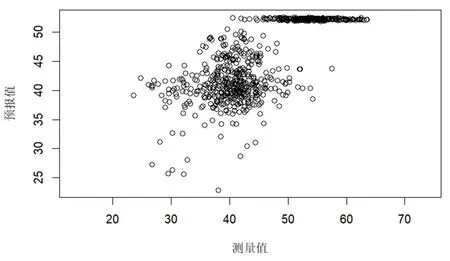
图5 偏最小二乘模型预测值与样本测量值散点图

3.2 最大信息系数比值反射率特征选择

3.2.1 基于最大信息系数的比值植被指数构造

构造光谱参数通常能够消除光谱中的背景噪声,提高光谱信息的利用效率[24],而比值植被指数RVI因为构造简单、计算方便,在植被光谱分析中应用最为广泛.文[25]根据直线方程、幂函数、指数函数的决定系数大小在众多的比值参数中寻找重要的部分,这种处理方式的局限性很明显,因为如果一个重要的比值指数的取值规律与叶绿素含量之间的关系并不是线性函数、幂函数、指数函数中的任何一种,那么在搜寻过程中就会产生遗漏.

由于并不能事先确定某个植被指数的取值规律与叶片叶绿素含量之间的具体关系是什么,故本研究使用普适性更强的最大信息系数(MIC)来挖掘重要的比值参数.MIC 的计算开销较大,如果对原始光谱中每一个离散波段的比值进行计算,那么350～2500nm 范围内需要处理的比值参数多达4626801 个.因此,本研究利用B 样条基函数,分段提取光谱曲线中的信息,考虑到离散光谱波段本身存在高相关性,这种处理方式既不会造成明显的信息损失,同时又能大大降低计算开销.

如图6 所示,通过100 个B 样条基系数概括光谱信息,计算100个基系数比值与对应样本SPAD值之间的MIC 系数.图6 中的小矩形色块是对应光谱区段所对应比值的MIC 值,MIC 值越趋向1,颜色越偏向于深红,表示对应光谱区段比值与叶片SPAD 值之间存在某种关系;MIC 值越趋向0,颜色越偏向于淡黄,表示对应光谱区段比值与叶片SPAD 值之间几乎没显示出任何关系.400～1000 nm 范围与1000～1800 nm 范围的光谱比值与叶片SPAD 值之间有密切联系,此外,350～500 nm 范围与500～900 nm 范围的光谱比值,以及1380～1500 nm 范围与1500～1800 nm 范围的光谱比值,与叶片SPAD 值之间关系密切.图7 为通过MIC 找到的两个典型的比值指数取值与对应样本SPAD 值的散点图,其中(a)横坐标: 440～463 nm 区间与531～553 nm 区间光谱反射率比值;(b)横坐标: 1187～1210 nm 区间与1798～1821 nm 区间光谱反射率比值.显然,样本SPAD 值确实随着光谱区间比值变化而变化,但是其变化规律却无法用某个已知函数准确表达.

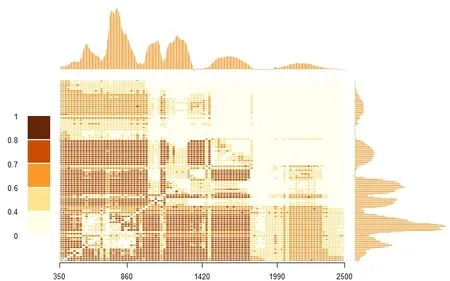
图6 基于B 样条基函数的比值参数与叶片SPAD 值的MIC 强度

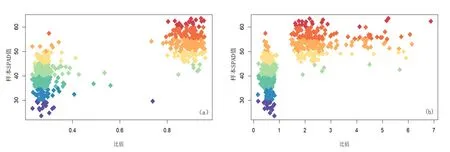
图7 两个典型的比值指数取值与对应样本SPAD 值的散点图

3.2.2 基于增强回归树的叶片SPAD 值预测建模

设定树复杂度(树的节点数)为5,学习率(learning rate)为0.005,同时为了降低计算时间开销,根据MIC 值大小,从100 个B 样条基系数两两之间的比值中挑选最大的2686 个,作为解释变量用于叶片SPAD值的增强回归树建模.所挑选的2686 个比值主要集中在400～1000 nm 范围与1000～1800 nm范围的光谱比值,350～500 nm 范围与500～900 nm 范围的光谱比值,以及1380～1500 nm 范围与1500～1800 nm 范围的光谱比值.最终共建立回归树1350 棵,图8 为最终的增强回归树模型交互验证预测情况,均方根误差为2.48,为SPAD 测量平均值的5.5%,已经接近实验数据的测量误差.对比于3.1 节中所采用的偏最小二乘方法,预测精确度提升十分明显.

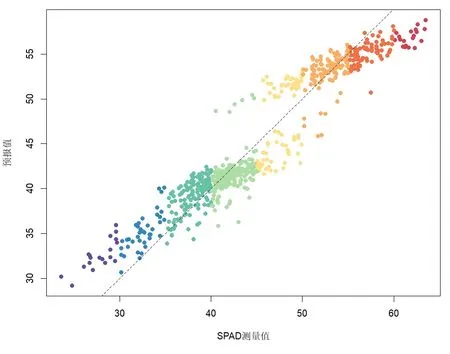
图8 增强回归树模型交互验证预测情况

4 结束语

为研究油菜冠层光谱的函数特征与叶片叶绿素含量之间的关系,本文以苗期、抽薹期和荚果期三个生长期的油菜为研究对象,利用B 样条基函数提取局部光谱片段的信息,构建比值植被指数,再利用增强回归树建立油菜叶片SPAD 值定量预测模型.油菜冠层光谱样品间的差异主要出现在各反射峰位置,但是这种差异对叶片SPAD 值的影响并非简单线性的,利用增强回归树模型则能够有效处理二者间的复杂关系,建立有效的SPAD 预测模型.