脉冲压缩技术在高温锻件电磁超声检测中的应用

汪树民,石文泽,卢 超,张 琦,程进杰,吴 健

(1.江西省检验检测认证总院 特种设备检验检测研究院 景德镇检测分院,江西景德镇 333000;2.南昌航空大学 无损检测技术教育部重点实验室,南昌 330038;3.江西省检验检测认证总院 特种设备检验检测研究院,南昌 330200;4.江西省检验检测认证总院 特种设备检验检测研究院 上饶分院,江西上饶 334000)

0 引言

大型铸锻件是电力、冶金、石化、造船、铁路、矿山、航空航天、军工等国家重大技术装备和重大工程建设所必需的关键基础部件,大型铸锻件制造业也是关系到国家安全和国家经济命脉不可或缺的战略性产业[1]。金属锻件的锻造温度通常在850 ℃以上,直接对锻造过程中的高温锻件进行缺陷无损检测,有利于在制造初期发现、修复和抑制缺陷,及时剔除缺陷超标残次品。因此,在高温锻造过程中实现缺陷的实时无损检测、控制和抑制,有利于提高锻件的锻造质量、经济水平和成品率[2-3]。

实现超高温铸锻件在线无损检测的关键在于耐高温传感器技术。常用高温检测技术有:压电超声、高温云纹干涉、电磁超声、激光超声、空气耦合超声等。由于电磁超声换能器(Electromagnetic Acoustic Transducer,EMAT)具有无需耦合剂、对待测金属表面粗糙度要求不高、易激发各种超声波、可检测较厚金属工件、成本低等优点,因此,电磁超声技术被国内外学者一致认为最适合而且已经被应用于高温铸锻件无损检测的关键性技术[4-11]。

通过增加EMAT探头提离、探头前端设置隔热材料[12]、采用水/油/空气冷却[13-14]、使用高居里温度的电磁铁[15-16]可以实现瞬态高温检测。然而,现有高温EMAT普遍存在高温耐受能力差、信噪比低、同步平均次数多等问题,很难应用于超高温大型铸锻件在线快速检测。

基于脉冲压缩技术的EMAT检测方法具有增强信噪比和空间分辨率的效果,已经成为国内外学者关注的热点。例如,HO等[17]引入脉冲压缩技术,实现了薄铝板在线快速厚度测量和成像检测;RICCI等[18]将脉冲压缩技术应用于高衰减的锻件超声检测,信噪比明显提高;LIZUKA等[19]将脉冲压缩技术应用于1 000 ℃以上高温铸坯液芯末端快速检测,取得较好的效果,但是技术细节尚不清楚;ISLA等[20]提出基于编码脉冲压缩技术的EMAT检测技术,在信噪比相同时,将激励电压由1 200 V降为4.5 V。

截止目前,脉冲压缩比最高可达1/20。由于超声回波的信噪比与激励脉宽平方根成正比,因此通过延长脉冲激励持续时间可以增强信噪比,还可以实现快速、大提离检测,从而提高EMAT高温耐受能力。

常见的编码形式有伪随机M序列、巴克(Barker)码、格雷(Golay)码等相位码,以及伪线性调频(Linear Frequency Modulation,LFM)信号、LFM信号和非线性调频(Non-Linear Frequency Modulation,NLFM)信号。最常用的Barker码的长度为13位,为了降低旁瓣水平,有必要对码元信号进行设计。若设计不当将可能导致该码元信号与EMAT作用后,发生明显的波形失真和带宽损失,信噪比和空间分辨率均遭受损失。鉴于此,本研究以提高高温锻件平底孔缺陷螺旋线圈电磁超声检测回波的信噪比和分辨率为研究目标,建立电磁超声检测过程的场路耦合分析有限元模型,通过数值计算和试验验证相结合,分析和比较LFM,Barker,LFM+Barker复合调制和调幅线性调频(Amplitude Modulation Linear Frequency Modulation,AMLFM)+Barker复合调制共4种调制信号的脉冲压缩技术的应用效果和优缺点。

1 螺旋线圈EMAT检测过程场路耦合有限元建模

1.1 螺旋线圈EMAT换能机理

基于洛伦兹力的螺旋线圈EMAT换能机理如图 1所示。在铁磁性金属材料中,洛伦兹力机理和磁致伸缩机理同时存在。圆柱形永磁体可以提供z向的静态偏置磁场,螺旋线圈主要提供r向动态磁场,因此螺旋线圈EMAT以洛伦兹力换能机理为主。基于洛伦兹力机理的超声波接收与发射过程互为逆过程,螺旋线圈EMAT检测过程有限元建模的控制方程见文献[21-22]。

1.2 EMAT激励等效电路模型

图 2为EMAT激励等效电路模型,主要由3部分构成:脉冲功率放大器、L型阻抗匹配、激励EMAT线圈等效阻抗。脉冲功率放大器可简化为阻抗为Zi=Ri+jXi、电压为U0的电压源,阻抗匹配网络为阻抗jXa和jXb的电容和电感组合,激励EMAT线圈可等效为ZE=RE+jXE。当调换功率放大器和EMAT线圈的位置,对应为阻抗匹配方式Ⅲ,Ⅳ。

选用阻抗匹配方式Ⅰ,Ⅱ且EMAT激励等效电路满足共轭匹配条件(阻抗Ri=RE,Xi=-XE)时,对应的阻抗匹配网络参数Xa,Xb可由下式求得:

(1)

其中:

(2)

式中,Q为阻抗匹配品质因数。

通常情况下,射频功率放大器部分的阻抗可视为Ri=50 Ω,Xi=0,故由式(2)可得当线圈内阻RE<50 Ω时,Q值才会存在,且此时阻抗匹配方式Ⅰ,Ⅱ分别对应Q值取“+”“-”。当相互对调射频功率放大器和EMAT的位置且Q值存在时,则Q>0和Q<0时,分别对应阻抗匹配方式Ⅲ和Ⅳ。

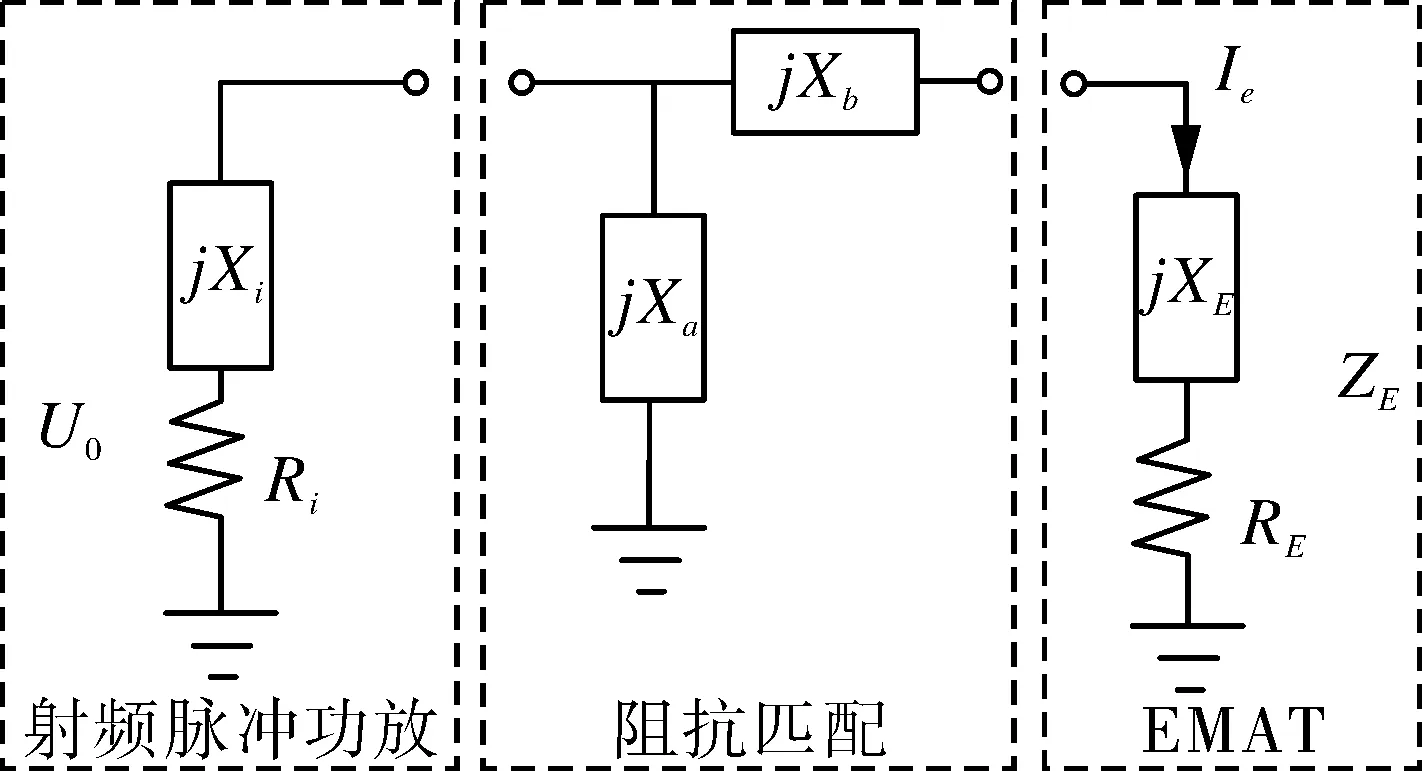
(a)阻抗匹配网络Ⅰ(Q>0),Ⅱ(Q<0)

1.3 场路耦合有限元建模流程

基于复合编码信号激励的EMAT检测过程场路耦合有限元建模流程主要分为两部分。第一部分是建立EMAT激励等效电路模型,获得EMAT的瞬态激励电流i(t)。以LFM信号为例,其函数表达式为:

(3)

式中,fc为LFM信号的中心频率;Bw为LFM信号的频带宽度;μ为频率变化斜率,μ=Bw/Pw;Pw为LFM信号的脉冲宽度。

将等效阻抗ZE(f)转变为时间t的拟合函数:ZE(f)=RE(t)+jXE(t);同时,根据图2给出的激励EMAT等效电路模型,由式(1)(2)可计算出不同阻抗匹配方式下的匹配元件参数(Xa和Xb)。采用幅值为U0的线性调频信号st(t)作为EMAT的激励电压代入等效电路模型,即可得到EMAT的瞬态激励电流i(t)。可以将LFM,Barker,LFM+Barker复合调制和基于幅度加权的AMLFM+Barker复合调制信号作为EMAT的激励电压。

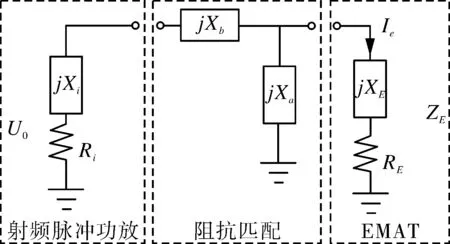
(b)阻抗匹配网络Ⅲ(Q>0),Ⅳ(Q>0)

第二部分是建立螺旋线圈EMAT的超声激励及传播过程有限元模型,求解超声波位移信号x(t)。模型输入信号为第一部分计算获得的瞬态激励电流i(t),通过多物理场耦合及超声振动位移传播和信号接收的模拟,计算超声波位移信号x(t)。最后,将瞬态超声位移信号x(t)与瞬态激励电流i(t)进行卷积,即可获得脉冲压缩信号y(t)。

1.4 螺旋线圈EMAT设计参数及有限元模型

螺旋线圈EMAT设计参数示意图如图3所示。其主要由圆柱形永磁体、螺旋线圈、含缺陷的碳钢试样等组成,各参数取值如表 1所示。其中,碳钢试样下方的ld线为缺陷处超声位移接收区域,与平底孔半径一致。

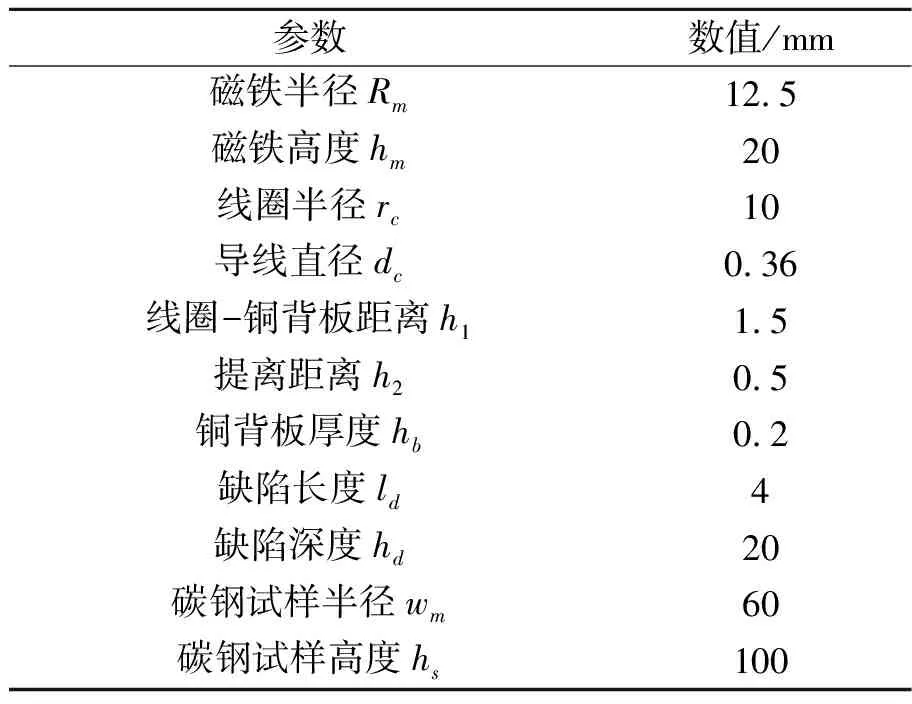
表1 螺旋线圈EMAT设计参数及其取值

图3 螺旋线圈EMAT设计参数示意

在螺旋线圈EMAT有限元模型中,永磁体及含平底孔缺陷的碳钢试样选用映射网格,螺旋线圈及空气域选用三角形网络。同时,螺旋线圈导线边界及碳钢试样上边界的换能区域采用边界层网络进行细化。有限元模型中的永磁体、碳钢试样、铜导线及铜背板的电磁学参数如下:永磁体、碳钢试样、铜导线、铜背板的相对磁导率分别为1.04,100,1.0,1.0,电导率分别为7.14×105,4.03×106,6.00×107,6.00×107S/m。

2 4种编码信号脉冲压缩技术在螺旋线圈电磁超声检测中的仿真研究

2.1 4种调制信号对应的激励电流

在激励EMAT等效模型中,由阻抗匹配方式Ⅰ获得的阻抗匹配参数,采用幅值为U0的LFM信号激励时,获得的4种调制信号激励电流见图4。其中,LFM+Barker信号、AMLFM+Barker信号的带宽与LFM信号带宽保证一致。

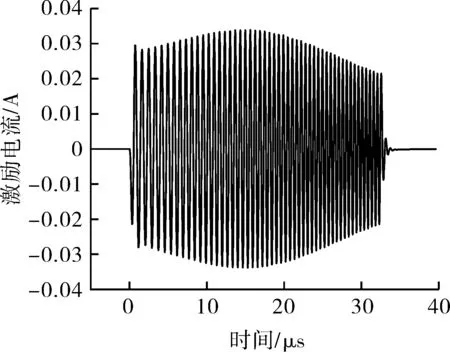
(a)LFM信号

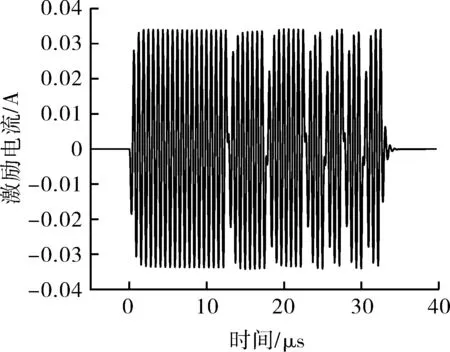
(b)Barker信号

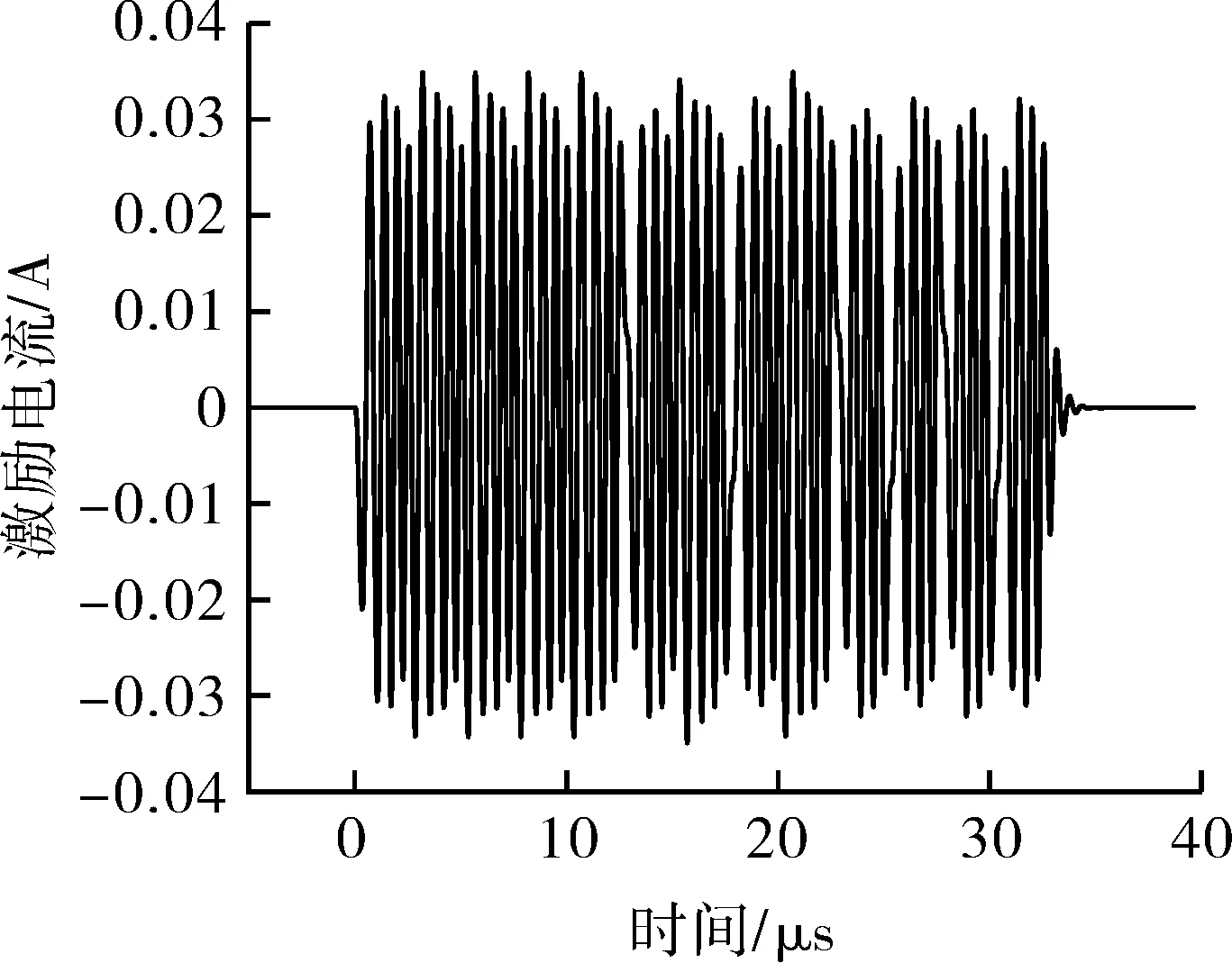
(c)LFM+Barker信号

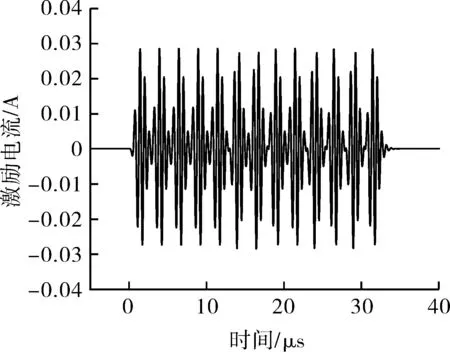
(d)AMLFM+Barker信号

2.2 4种调制信号的脉冲压缩效果对比

将瞬态激励电流i(t)代入建立的螺旋线圈EMAT超声激励及传播过程有限元模型,采用瞬态求解计算可得缺陷处ld拾取的超声振动位移信号x(t),如图5所示。可以看出,缺陷处横波透射波信号与电流激励信号的波形差异主要是因为螺旋线圈EMAT的声场特性随着激励频率而变化。

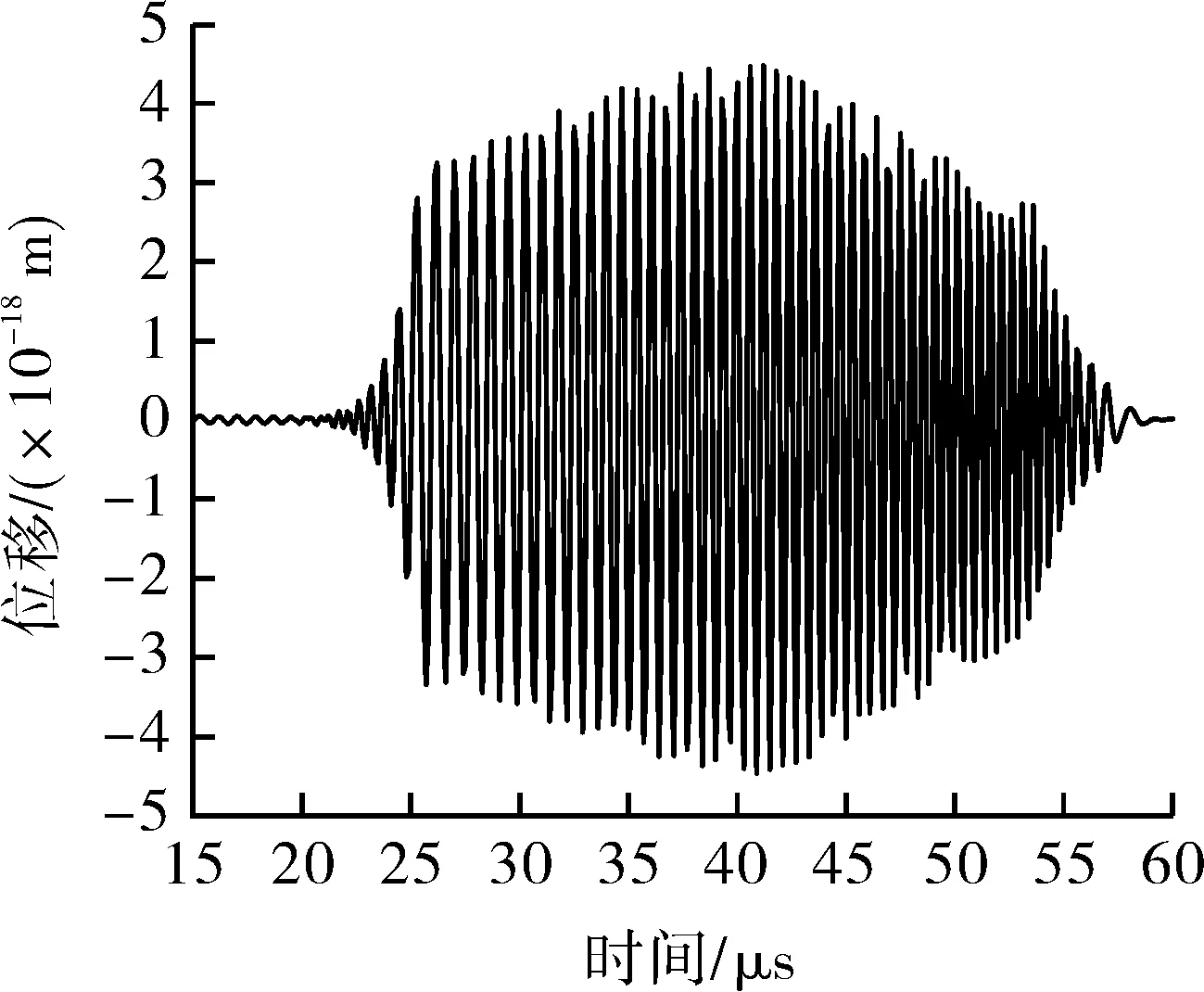
(a)LFM信号

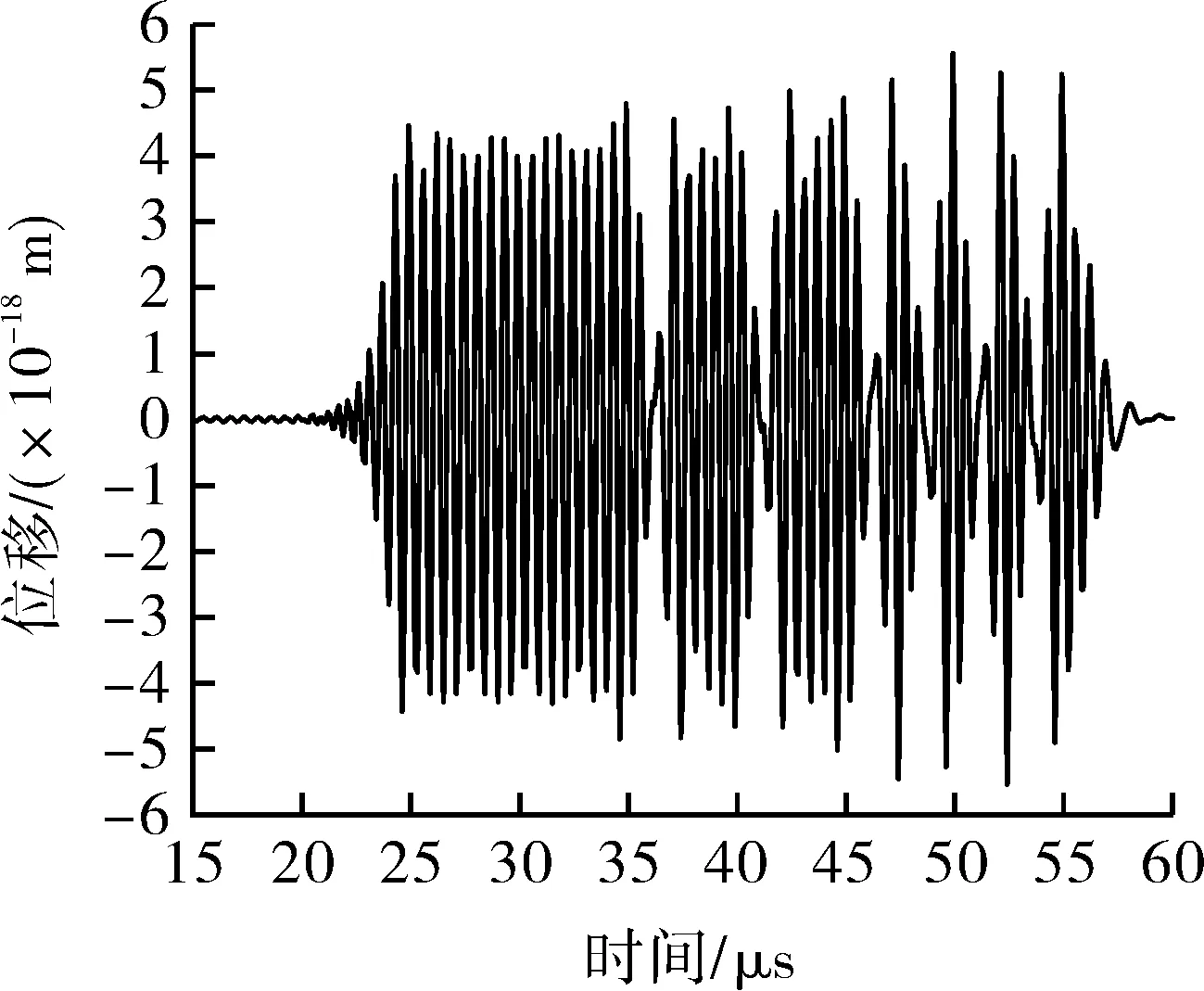
(b)Barker信号

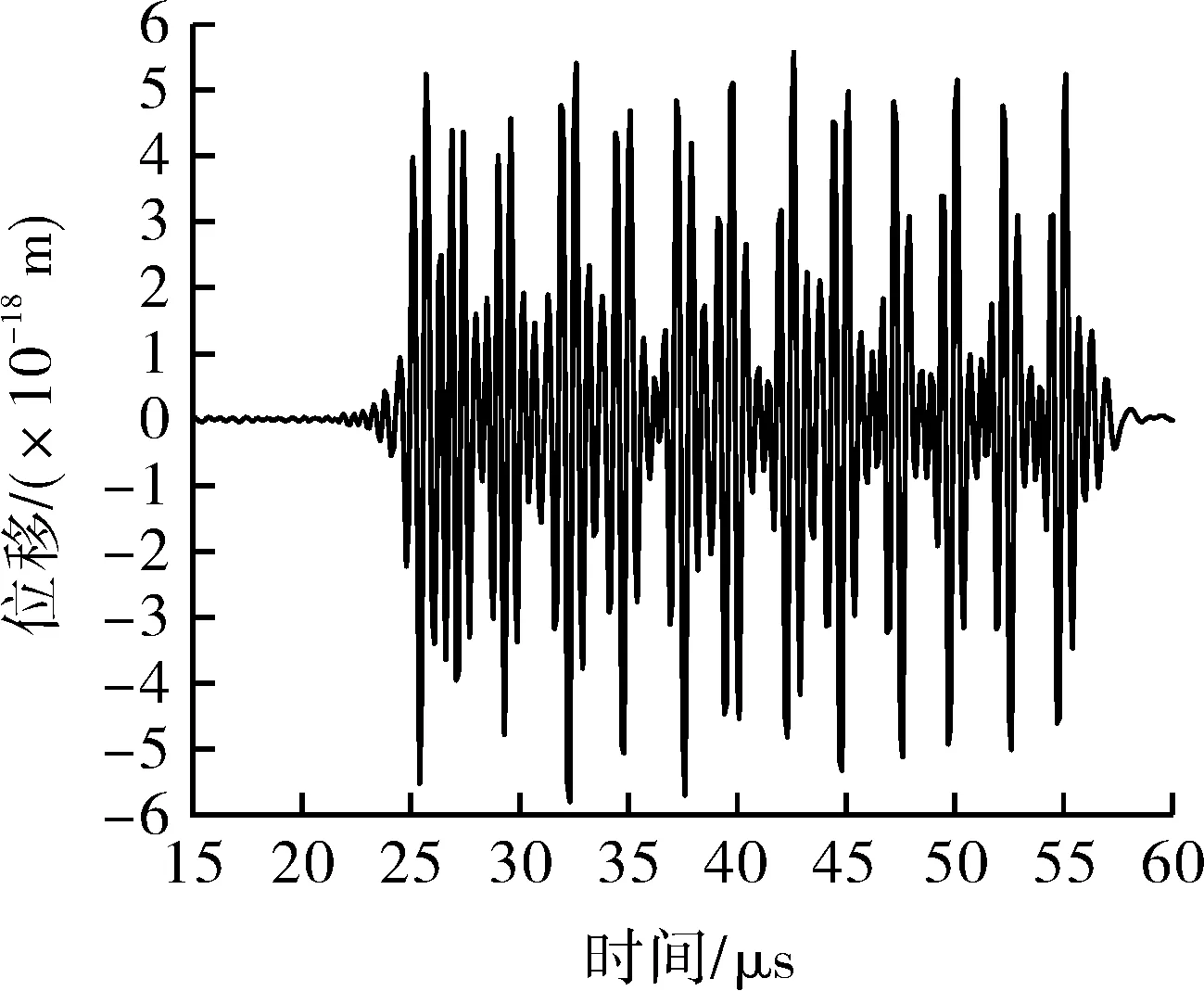
(c)LFM+Barker信号

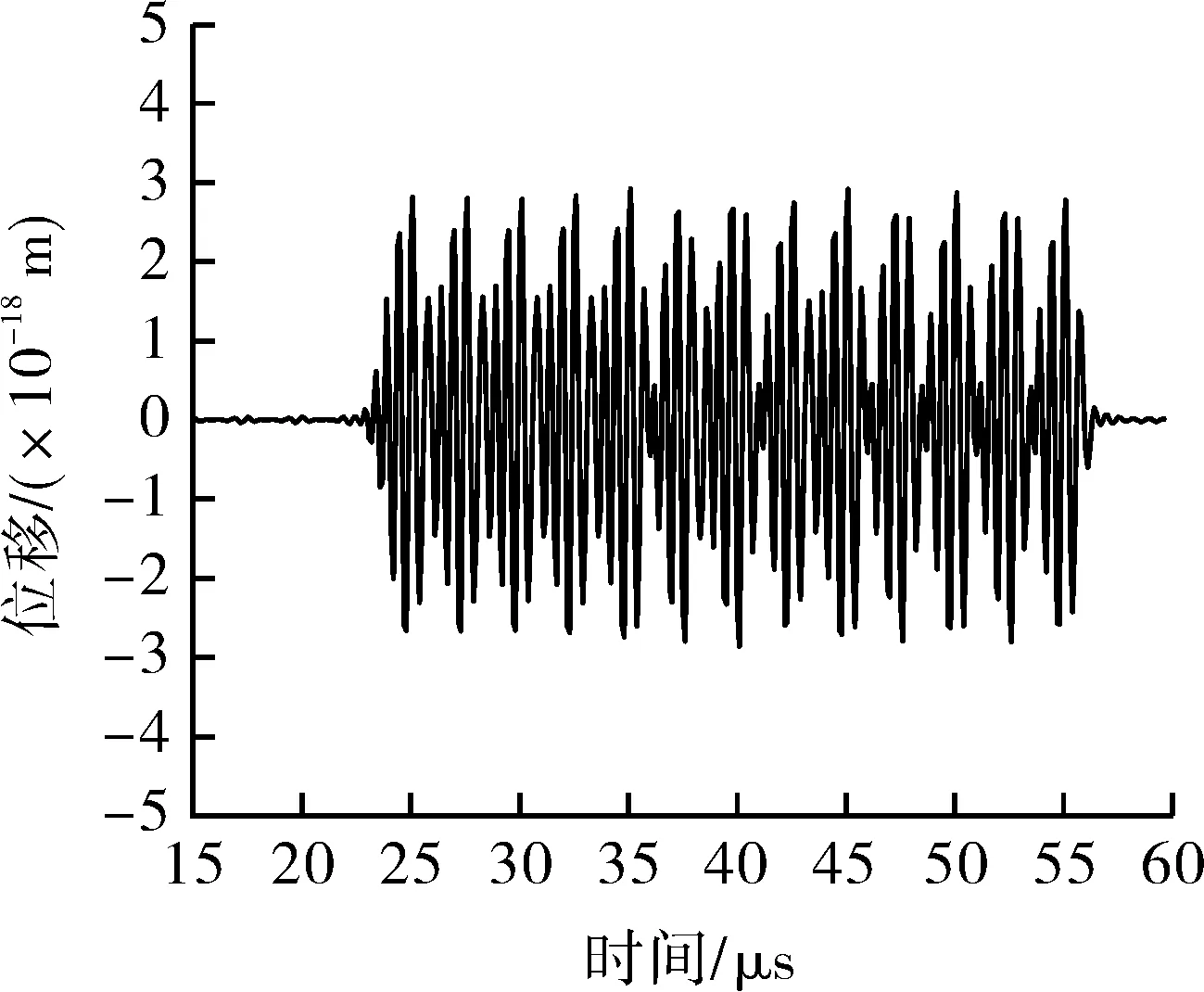
(d)AMLFM+Barker信号

此外,AMLFM+Barker信号由于子脉冲LFM信号加窗的影响,拾取的缺陷处超声位移信号幅值明显小于其他三者。

将计算获得的缺陷处瞬态超声位移信号x(t)与瞬态激励电流i(t)进行卷积即可获得脉冲压缩信号y(t),不同调制信号激励时匹配滤波器输出的脉压信号如图 6所示。可以看出,采用LFM+Barker信号或AMLFM+Barker信号激励时获得的脉压信号的主瓣和旁瓣形状与Barker信号激励的脉压信号形状一致,均为主瓣两侧均匀分布着6个旁瓣。此时,脉压信号主瓣幅值大小为:Barker(1.92×10-17m)> LFM+Barker(1.50×10-17m)> LFM(1.44×10-17m)>AMLFM+Barker(0.58×10-17m)。取缺陷处脉压信号的上包络曲线,分别进行归一化,由-6 dB法获得的主瓣宽度大小为:Barker(2.83 μs)>LFM+Barker(2.62 μs)>AMLFM+Barker(2.15 μs)>LFM(1.82 μs)。

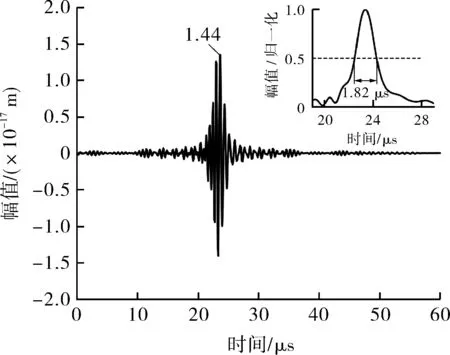
(a)LFM信号 (b)Barker信号

(c)LFM+Barker信号

3 试验验证

3.1 试验系统

锻件螺旋线圈EMAT检测试验系统如图7所示。试验采用的4种调制信号可由任意信号发生器AFG-2022B产生,经RITEC-4000功率放大器进行功率放大,输出信号经阻抗匹配作用于EMAT上。接收到的微弱超声回波信号经过带通滤波器和前置放大器完成滤波放大功能,再经过数据采集卡完成模数转换,最终数据在安装有LabVIEW软件界面完成存储与分析。

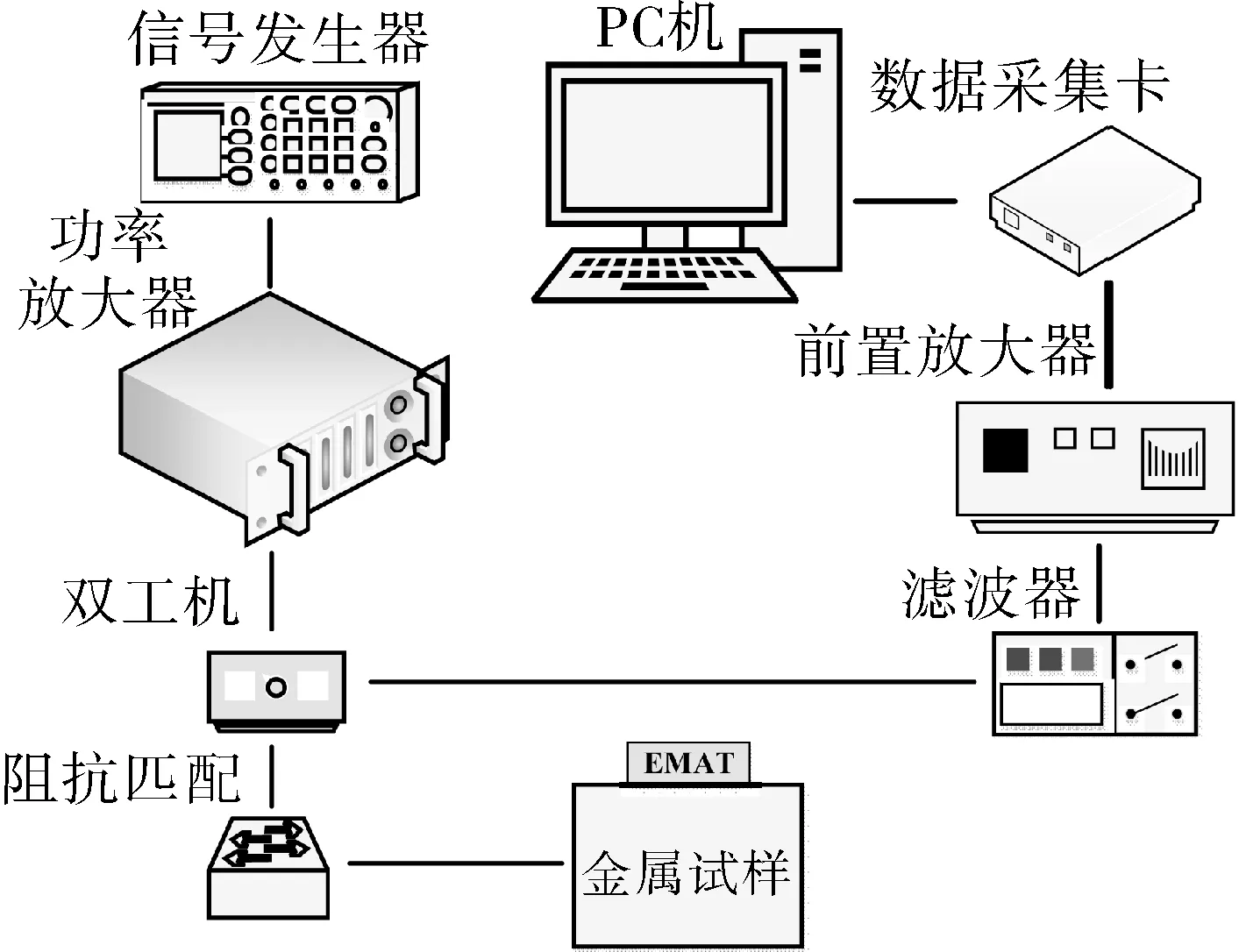
图7 锻件螺旋线圈EMAT检测试验系统

图8 高温锻件与螺旋线圈EMAT探头

(d)AMLFM+Barker信号

高温锻件与螺旋线圈EMAT探头如图 8所示。激励信号分别选用中心频率1.6 MHz的LFM信号、Barker信号、LFM+Barker信号及AMLFM+Barker信号,选用的调制信号时宽统一设置为32.5 μs。高温锻件的长、宽、高分别为160,160,100 mm,底面预制有直径∅8 mm平底孔缺陷,埋深为80 mm。

3.2 高温检测结果分析

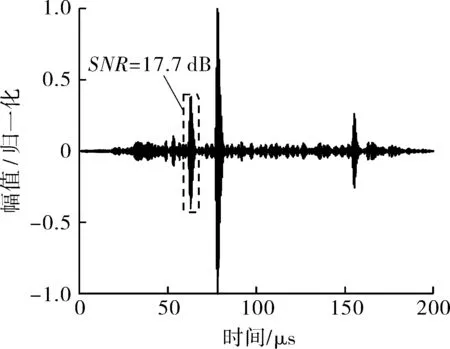
选用中心频率1.6 MHz的LFM信号、Barker信号、LFM+Barker复合调制信号及AMLFM+Barker复合调制信号作为激励信号,获得650 ℃高温锻件内部缺陷对应的超声回波信号如图 9所示。当高温锻件温度为650 ℃,4种调制信号对应的缺陷波信噪比分别为15.8,17.9,16.1,17.7 dB。

表2列出450～650 ℃高温锻件的缺陷波的信噪比。可以看出,4种调制信号激励时获得的缺陷波信噪比随温度非线性变化,大致呈现先缓慢增加、再降低的趋势。在LFM,Barker,LFM+Barker,AMLFM+Barker这4种调制信号中,LFM调制信号对应的信噪比总体较差;Barker和LFM+Barker两种调制信号对应的信噪比大体接近;AMLFM+Barker调制信号在锻件温度≤550 ℃时,保持较高的信噪比,但当锻件温度>550 ℃时,信噪比下降明显。

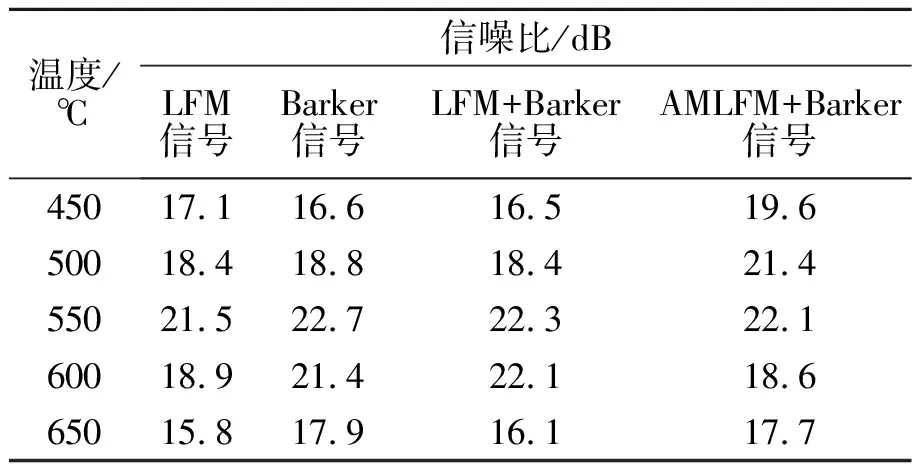
表2 4种调制信号对应的缺陷波信噪比

(a)LFM信号 (b)Barker信号

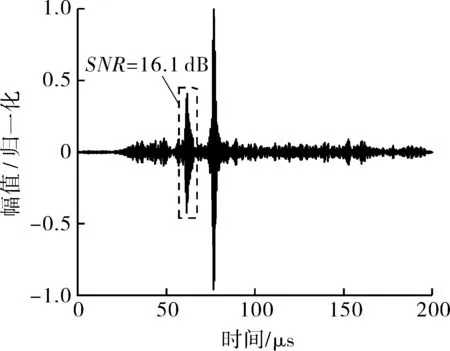
(c)LFM+Barker信号

表3列出450～650 ℃高温锻件的缺陷波主瓣宽度。可以看出,LFM+Barker信号激励时获得的缺陷波主瓣宽度最小,其均值约为2.0 μs,空间分辨率最高;AMLFM+Barker信号由于子脉冲(LFM信号)加窗的影响,故主瓣宽度有所增加;Barker信号激励获得的缺陷波主瓣宽度均值约3.50 μs,其空间分辨率最差,这与仿真结果相一致。除LFM调制信号以外,Barker,LFM+Barker,AMLFM+Barker三种调制信号对应的信噪比区别不大,关键的区别在于LFM+Barker调制信号对应主瓣宽度总体上最小,因此基于LFM+Barker复合调制信号的脉冲压缩技术兼具高主瓣信噪比和高空间分辨率的优点。与传统单脉冲激励方式相比,将脉冲压缩技术应用于高温锻件平底孔检测,可以显著提高信噪比和空间分辨率。提高信噪比有利于增强缺陷检测灵敏度。减小主瓣宽度有利于提高缺陷检测分辨率,也就对应着相邻多个缺陷或缺陷与底面距离较近时的空间分辨能力。

表3 4种调制信号对应的缺陷波主瓣宽度

4 结论

(1)针对脉冲压缩技术应用于电磁超声检测时,检测系统频谱特性与复合编码信号带宽不匹配,导致脉冲压缩效果下降的问题,通过数值仿真和试验验证相结合,分析和比较了LFM,Barker,LFM+Barker复合调制和基于幅度加权的AMLFM+Barker复合调制共4种调制信号的脉冲压缩技术的应用效果和优缺点。

(2)本研究通过仿真分析和试验验证发现:LFM+Barker复合调制脉冲压缩技术兼具高信噪比和高分辨率的优点,将该技术应用于高温环境下铸锻件超声检测,有助于进一步提高小缺陷的检测能力和缺陷检测的分辨率。