R6和RSE-M规范中一次应力与二次应力作用下的裂纹驱动力计算方法对比分析
2023-11-07王大胜鲁治诚
王大胜,金 挺,徐 晓,鲁治诚
(1.核电安全监控技术与装备国家重点实验室,广东深圳 518124;2.深圳中广核工程设计有限公司,广东深圳 518124)
0 引言
核电厂设备承受的载荷总体上可以分为一次应力载荷和二次应力载荷,其中一次应力为平衡外载所必需的应力,会导致结构发生塑性垮塌失效,不具有自限性,其主要由机械载荷(典型的如内压、轴力、弯矩)和自重引起;二次应力是由相连部件的约束或结构的自我约束所产生的应力,二次应力具有自限性和自平衡特征,典型如结构壁厚温差导致的热应力和筒体(管道)对接焊缝的焊接残余应力等,同时载荷还会引起结构上产生峰值应力[1-3]。
对承受一次和二次应力载荷的含裂纹设备开展断裂分析评价时,需要首先分析计算裂纹的驱动力参数(应力强度因子(SIF)K或者J积分)。 满足线弹性断裂力学分析条件时,计算线弹性SIF,对一次应力和二次应力引起的SIF值可以直接线性相加,相对比较比较简单,采用线弹性断裂力学分析理论需要关注其适用条件;当需要按照弹塑性断裂力学开展分析时,则需要计算断裂参数J积分值,由于随着塑性程度不同,一次应力和二次应力的相互作用特点不同,二次应力对弹塑性断裂参数J积分的贡献也会随着塑性(载荷大小)程度而发生变化,因为随着塑性变形增大二次应力可能会发生松弛或者重分布,进而影响J积分的结果[4-6]。因此,对一次应力和二次应力共同作用时,量化二次应力对弹塑性断裂的影响,可靠地评估弹塑性J积分或者等效SIF对含缺陷设备的弹塑性断裂力学分析评估十分重要。
核电常用规范RSE-M和R6规程中均提供了针对一次应力和二次应力相互作用下的裂纹驱动力计算方法。基于参考应力法[7-8],R6规程中提供了针对一次应力和二次应力相互作用下的SIF计算方法,已有大量的研究者通过有限元分析[6,9-13]来验证和优化R6规程中提供的分析方法,LEI等[6]研究了在断裂评估中对残余应力的处理方法,研究中使用有限元方法评估了EPRI和参考应力两种J积分估算方法,同时还对R6缺陷评估程序中的二次应力(包括残余应力)的处理进行了分析。AINSWORTH[9]回顾了合于使用规范和文献中V系数的评估方法,以考虑裂纹尖端塑性引起的一次应力和二次应力之间的相互作用,并提出了一种基于松弛方程的新方法,新方法与具有和不具有显著弹性随动的二次应力有关:当弹性随动明显时,二次应力具有一次应力的特征,在没有弹性随动的情况下,导出了一种与二次应力大小无关的包络V系数计算方法;OH等[10]对管道环向裂纹考虑机械载荷和热载荷情况,采用弹塑性有限元分析方法验证计算了R6中弹塑性J积分计算方法,分析结果表明当二次应力较大时,加载瞬态将明显影响弹塑性J积分的计算结果,但是采用R6最新推荐的方法可以保守考虑这种结果。AINSWORTH等[11]对残余应力对断裂行为的影响进行了研究,发现残余应力对断裂行为的影响取决于构件中的塑性水平。在弹性占主导的情况下,残余应力将明显降低含缺陷结构的承载能力,相反,当大范围在塑性状态时,残余应力的影响则会降低到最小。PAN等[12]对处理工程失效评估中的二次应力的ρ因子进行了试验验证,并推荐了较R6中更合适的方法。SONG等[13]对于一次应力和二次应力组合并且有明显弹性随动情况时,推荐采用V系数用于计算J积分,其采用3个参数来表征弹性随动,分别为一次应力和二次应力的相对大小参数β及Vo-β曲线的初始斜率参数,并分析了弹性随动效应的影响因素及存在明显弹性随动情况时V计算的近似表达式。NAM等[14]以含环向表面裂纹的容器承受轴向拉伸和径向温度梯度载荷作用为分析对象,分别采用R6和法国A16合于使用规程提供的弹塑性J积分计算方法及有限元分析方法计算了环向裂纹和环向半椭圆裂纹的J积分,并对不同方法得到的J积分计算结果进行了对比分析。在有限元分析中,机械载荷和热载荷的相对大小和加载顺序以及材料应变硬化指数都进行了系统性变化考虑,分析结果表明,R6估计总体上是准确的,但在大Lr时可能存在非保守性,A16估计在小Lr和大Lr时均是保守的,文中还讨论了R6和A16中保守和非保守的可能来源。陈明亚等[15]针对材料拉伸性能符合R-O关系的结构,基于英国R6规范的双参数失效评定图(FAD)技术,采用理论推导的方法,提出一种线弹性断裂参量应力强度因子(SIF)的塑性修正方法,分析案例表明,焊接和矫形过程形成的残余应力对结构断裂性能存在明显影响。经过大量研究者的分析验证和优化,目前R6规程中提供的分析方法能够保守地用于大部分含裂纹金属结构的断裂分析评价。

1 材料属性
假设材料的单轴拉伸应力-应变曲线满足Ramberg-Osgood (R-O)关系:
(1)
式中,σy为屈服强度,取材料0.2%应变对应的应力;α,n为R-O模型的硬化系数和硬化指数,为了和σy为的定义保持一致,因此取α=0.002E/σy。
根据典型核电承压设备材料在高温下的材料性能,本节假设σy=300 MPa,E=200 000 MPa,为了对比不同真应力-应变材料属性对SIF塑性修正的影响,分别采用不同n系数材料属性数据,分别选取n=5,10两种假想材料属性。其中,n越小,材料的应变强化效应越明显;n越大,材料越接近理想弹塑性材料。
2 RSE-M中的分析方法
在RSE-M规范中基于线弹性断裂力学计算一次应力和二次应力引起的SIF,采用式(2)得到等效的弹性J积分Je,考虑裂纹尖端的塑性应变,对SIF或者弹性J积分值进行塑性修正。RSE-M提供了分别计算一次应力和二次应力导致的SIF及等效的J积分,再分别进行修正的方法,在对二次应力引起的等效J积分进行修正时考虑一次应力的影响,从而得到弹塑性J积分值如式(3)所示。该方法与R6具有相似性,本文重点研究该方法并与R6进行对比分析。
(2)
式中,E′为弹性模量,E′=E/(1-υ2),其中υ为泊松比。
(3)
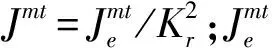
根据SIF和等效J积分转换关系式(2)可知,RSE-M中定义的参数Kr实质上是一次应力引起的SIF的塑性修正系数的倒数。RSE-M中提供Kr的计算式如下:
(4)
其中:
(5)
式中,σref为参考应力;εref为真应力-应变曲线上σref对应的应变值;Lr为衡量结构发生塑性垮塌失效的风险的参数。
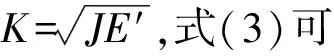
(6)
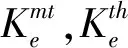
kth=Min[1;0.5+0.5exp[-0.46(Lth-1)]]
(7)
式中,Lth为尺寸参数,其与二次应力大小及裂纹尺寸相关,详细计算见RSE-M附录5.4,本文不再赘述。
(8)
式中,σth为应力-应变曲线上应变为εth对应的应力值;εth为热应力引起的应变。
结合材料的应力-应变曲线特征,可知σth/(Eεth)≤1。
通过对kth计算公式的分析,可知kth是0.5~1的一个系数,采用式(7)和式(8)计算得到的kth变化如图1、图2所示。
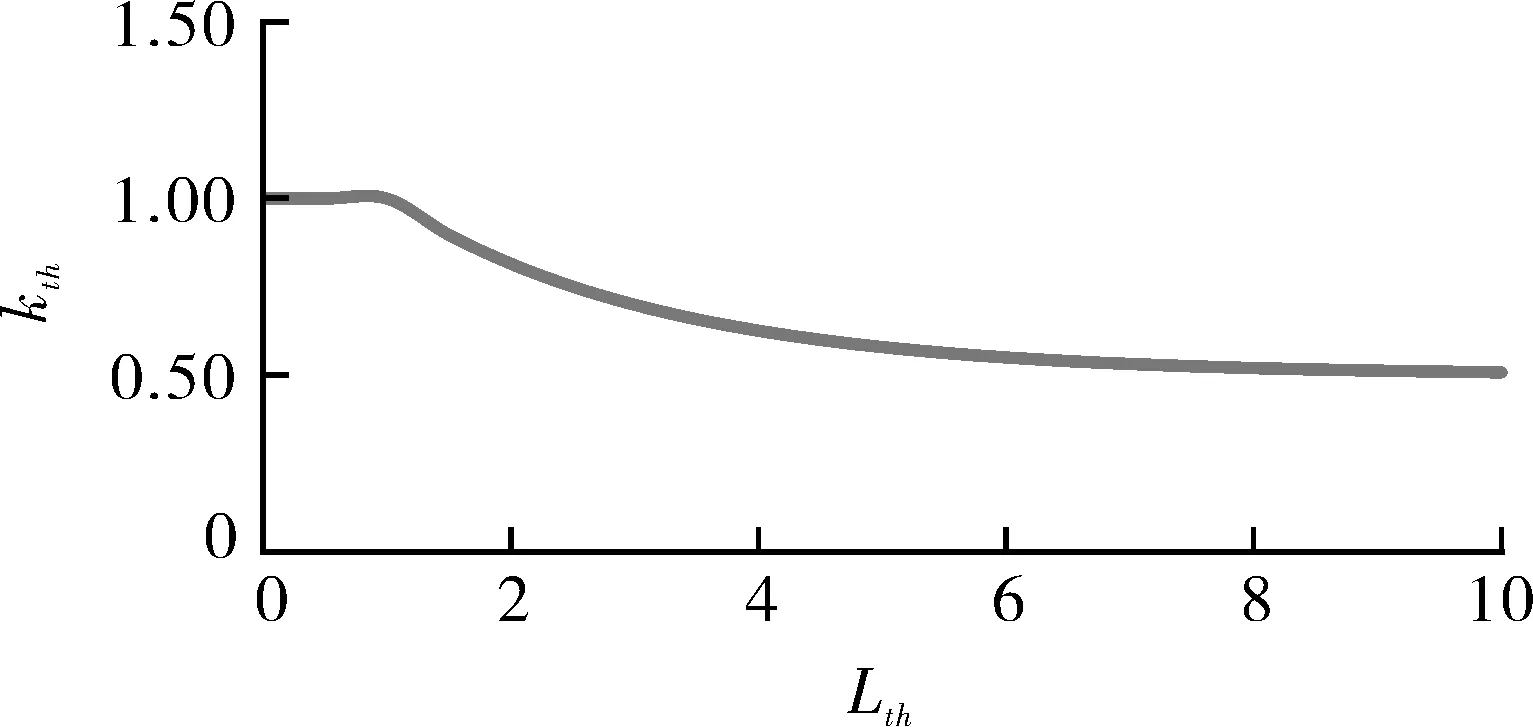
图1 式(7)计算kth的结果(无材料应力-应变数据)
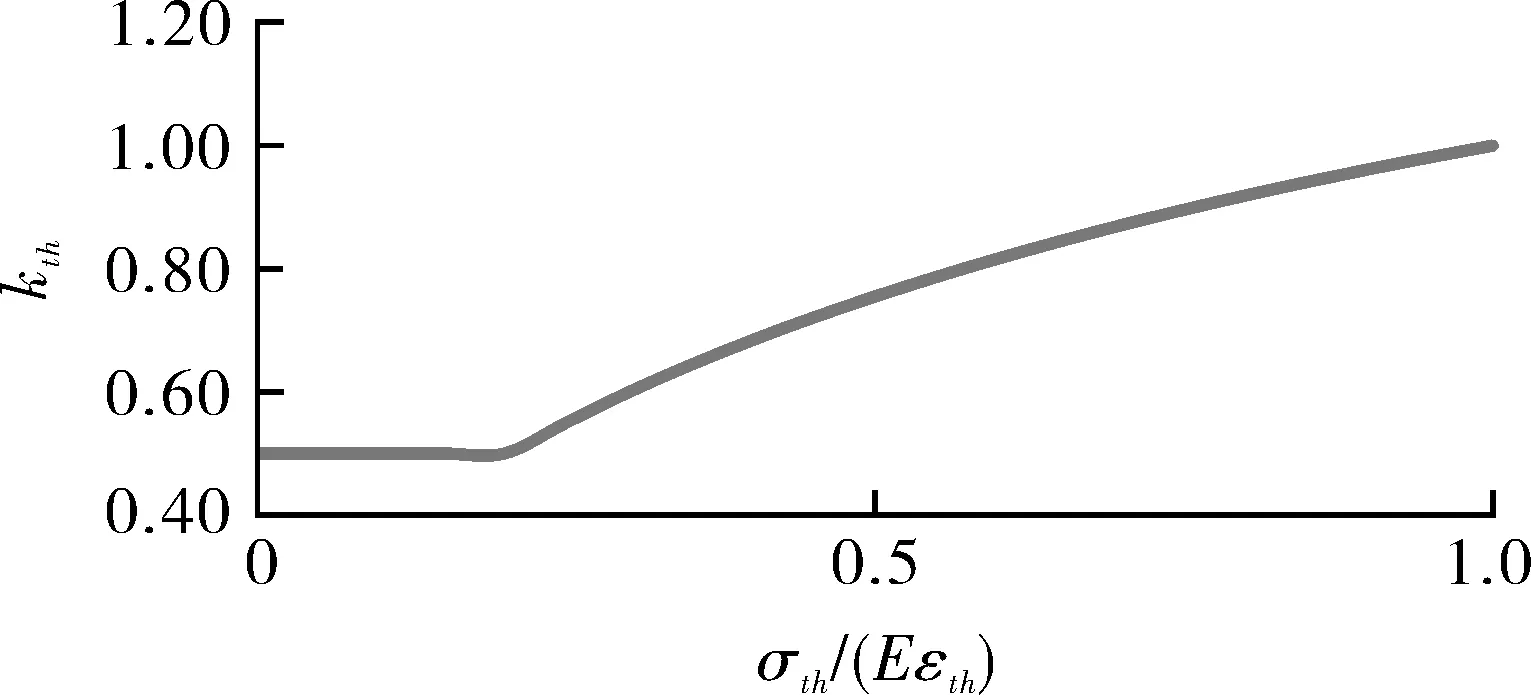
图2 式(8)计算kth的结果(有材料应力-应变数据)
通过分析可知,kth体现了自平衡的二次应力在塑性区应力重分布对SIF或者J积分的影响。
3 R6中的分析方法及与RSE-M的对比分析
3.1 R6中的分析方法介绍
R6规程中采用V系数来计算一次应力和二次应力相互作用下等效SIF,如式(9)所示,并且R6中提供的分析方法对结构形式没有限制。
(9)
式中,Kp为一次应力引起的线弹性SIF;Ks为二次应力引起的线弹性SIF;f(Lr)为R6中的失效评定曲线(FAC)。
R6中共提供了3种FAC曲线,选项1如式(10)、选项2如式(11)、选项3如式(12)所示。其中选项1为简化包络的FAC曲线,选项2为根据材料应力-应变曲线计算得到的FAC曲线,选项3中Je为线弹性J积分,J为弹塑性J积分,根据具体案例具体分析得到。选项1的FAC和采用n=5和n=10材料应力-应变数据计算选项2的FAC曲线随参数Lr的变化如图3所示。值得注意的是,按照R6规程,针对不同类的材料FAC有不同的截止值,由于本文分析不针对具体的材料,因此图中未标注FAC的截止值,在应用时需关注。
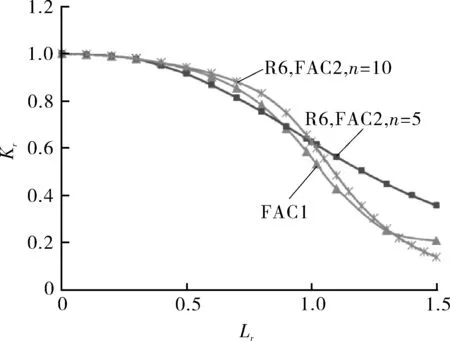
图3 R6中的FAC曲线
f1(Lr)=(1+0.5Lr2)-1/2[0.3+0.7exp(-0.6Lr6)]
(10)
(11)
(12)
FAC曲线计算公式中的Lr的含义与RSE-M中的一致如式(5)所示,是衡量结构发生塑性垮塌失效的风险的参数。通过分析式(12)及SIF与J积分的转换关系可知FAC曲线的物理含义实质上为一次应力引起SIF塑性修正系数的倒数,与上述RSE-M中的Kr的含义相同。
对式(9)中的V系数,R6提供多种计算方法,包括简化计算方法、详细计算方法、明显弹性随动下的计算方法和有限元分析方法等,其中简化计算方法和详细计算方法适用于弹性随动现象不明显的情况。
(1)简化计算方法。
简化方法中V系数计算式如下:
(13)

(14)
(2)详细计算方法。
R6中详细计算方法如下:
(15)
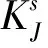
(3)存在明显弹性随动现象时的计算方法。
当存在明显弹性随动现象时(弹性随动因子Z>3时),R6推荐采用下式评估V系数。
(16)
R6提供的V系数简化计算方法和详细计算方法适用于大部分工程情况,并且是保守的。在满足某些特定情况时结构会出现明显弹性随动现象,根据文献[9,13]中的研究分析,发生明显弹性随动现象需要满足Lr比较小(<0.9)时,材料应变强化效应不明显(接近理想弹塑性材料),βs较小(βs<1)并且二次应力呈现薄膜应力时,才会出现了比较明显弹性随动现象。因此,本文重点分析R6提供的V系数简化计算方法和详细计算方法。
采用R6提供的V系数计算方法得到的V系数结果如图4所示,图中分别给出了βs=0.5和βs=3.0情况采用简化计算方法,采用选项1的FAC曲线和采用选项2的FAC曲线同时材料属性n分别等于5和10情况下的详细计算方法得到的V系数随参数Lr的变化曲线,各方法计算得到V系数随Lr的变化规律基本一致,同时受二次应力和材料属性影响。结合V系数计算公式可知,V系数的大小与一次应力和二次应力的大小均相关,并且一次应力的影响起主导作用,与二次应力的大小(βs)弱相关;系数V在Lr较小时(约小于0.9)大于1,在Lr较大时快速减小表现出二次应力发生明显的应力松弛效应。不同方法计算得到V系数结果差异不大。

图4 R6中V系数计算结果
3.2 R6与RSE-M的对比分析
根据R6中计算等效弹塑性SIF的式(9)和RSE-M中计算等效弹塑性SIF的式(6),以及R6和RSE-M对一次应力和二次应力的SIF修正系数的计算公式,进行对比分析。
(1)对一次应力的引起的SIF的塑性修正。
根据式(6)和式(9)可知,RSE-M和R6分别采用1/Kr和1/f(Lr) 对一次应力引起的SIF进行塑性修正,而根据式(4)和式(11)的对比分析可知,Kr和FAC曲线f(Lr) 的本质是相同的,均是基于参考应力法进行的修正。采用不同材料属性利用式(4)和式(11)进行计算的结果如图5所示,其中横坐标为Lr,纵坐标为Kr和FAC的值(在工程应用中需关注R6针对不同类的材料FAC设置有不同的截止值)。
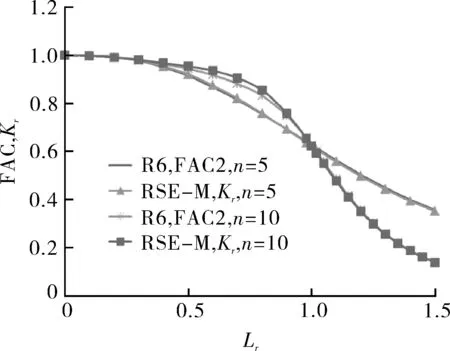
图5 R6中f(Lr)与RSE-M中Kr计算结果对比分析
根据计算结果可知,采用相同的材料属性计算得到Kr和FAC的值及随Lr的变化规律和结果基本相同,在文献[8]也研究指出RSE-M中Kr的计算方法源自R6,但是基于有限元分析进行了一定的修正。
(2)一次应力和二次应力共同作用下对二次应力引起SIF的修正。

(17)

4 结论
对承受一次应力和二次应力载荷共同作用下的含裂纹结构,需要考虑材料塑性及一次应力与二次应力的相互作用对裂纹驱动力计算的影响,对比了RSE-M规范和R6规程提供裂纹驱动力计算及对一次应力和二次应力引起裂纹驱动力的修正方法,研究了两种分析方法的理论、特点及异同。
(1)对一次应力引起的SIF(或弹性J积分),RSE-M和R6分别采用系数1/Kr和1/f(Lr) 进行修正,两种修正方法均基于参考应力法,得到的修正结果基本相同,1/Kr和1/f(Lr)实质上是对一次应力引起的SIF的塑性修正系数。

②系数V的计算中一次应力起主导作用,与二次应力的大小弱相关,系数V在Lr较小时(约小于0.9)大于1,在Lr较大时快速减小表现出二次应力发生明显的应力松弛效应;
③RSE-M适用范围限定于管道、平板和弯管结构,并且适用于没有或者少量弹性随动的情况,而R6提供分析方法的适用性对结构没有限制,同时考虑出现了一定程度弹性随动现象的情况,适用范围更大,同时分析结果也更为保守。
