城市轨道交通基于连续测量法的车辆曲辐板测力轮对组桥方案*
2023-11-07蔡昌俊何治新邓东强张胜龙沈凯明
蔡昌俊 何治新 陶 涛 邓东强 张胜龙 沈凯明
(1.广州地铁集团有限公司, 510330, 北京; 2.铁科院(北京)工程咨询有限公司,100081, 北京∥第一作者, 正高级工程师)
轮轨力是评价车辆动力学性能的重要指标。准确测量轮轨间的相互作用力,对城市轨道交通车辆的行车安全具有重要意义。测力轮对技术中的连续测量法是将多枚应变片粘贴在轮对辐板的特定位置上,并将其组成多个电桥。当轮对受恒定载荷作用时,电桥输出的结果通过解耦计算后具备恒定的峰值。相较间断测量法,采用连续测量法得到的轮轨力数据更加准确与稳定,是目前测量轮轨力最为精确的方式[1]。
文献[2]通过在车轮辐板的3个半径上确定合理的贴片位置和电桥桥路设计,消除车轮转动中角度变化带来的影响,建立包含垂向力、横向力及作用点位置等3个变量的多个非线性方程组进行求解。文献[3]通过轨道车辆轮对上载荷、弯矩及应变三者之间的转换关系,提出一种轮轨力连续测试方法。制作1∶5 的测力轮对实物模型,并在1∶5 转向架试验台上测试,最终获得该测力轮对的轮轨力。但该试验台在标定试验中采用的是静态标定的方法,仅能对几个特征点进行标定,故得到的标定数据缺乏连续性。文献[4]引用无迹卡尔曼滤波和线性卡尔曼滤波结合的方法改进了解耦算法。但在动态标定试验中采用的电桥仅由4组对称应变片组成,未研究多组应变片组桥方案对连续测量法的测力轮对测量精度的影响。
为提高连续测量法测力轮对的测量精度,本文针对曲辐板轮对分析了多组应变片组桥方案的测量精度,并采用动态标定的方式对轮对进行全角度的连续标定,最终提出准确、稳定的新型连续测量法测力轮对组桥方案。
1 测力轮对电桥应变响应静载试验
提升轮轨力测量精度的关键在于弱化横向力与垂向力间的耦合作用,合适的组桥半径可以显著降低该种耦合作用,凸显单一方向作用力的响应[5-6]。为了确定上述合适的组桥半径,本文设计了1/4电桥应变响应的静载试验。试验中采用半径R为420 mm的曲辐板轮对,沿轮对的径向粘贴1列应变片。轮对1/4电桥应变响应的静载试验如图1所示。

a) 曲辐板轮对实物
对轮对分别施加10 kN、20 kN、30 kN的横向力FT,以及30 kN、50 kN、70 kN的垂向力FV。沿径向分布的1/4电桥提取垂向、横向载荷下曲辐板内侧不同半径处的应变值,得到车轮内侧应变沿径向的变化曲线,如图2所示。
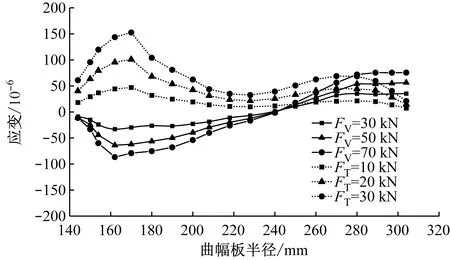
图2 不同荷载作用下轮对曲辐板内侧应变沿径向的变化曲线
由图2可见:在横向力作用下,车轮内侧的横向应变响应随着半径的增大,大致呈现先增大后减小的趋势;在垂向力作用下,车轮内侧的垂向应变响应大致呈现从负应变逐渐减小,而后转为正应变逐渐增大的趋势。在半径170 mm处,应变片对横向力作用的响应最大,对垂向力作用的响应较小,故横向力电桥的组桥半径RT宜为170 mm;在半径300 mm处,应变片对垂向力作用的响应较大,且对横向力作用的响应较小,综合考虑宜将垂向力电桥的组桥半径RV定为300 mm。
2 基于梯度下降法的测力轮对组桥方案分析
2.1 梯度下降算法原理
基于第1节中得到的最优组桥半径,利用梯度下降算法对组桥方案进行优化。
梯度下降法又称最陡下降法,是机器学习算法中广泛使用的一阶最佳化算法[7]。梯度下降法的计算流程如图3所示。
如图4梯度下降法示意图所示,假定目标函数为f(x),并设定该函数梯度下降的起始点坐标为(x0,f(x0)),单次下降的步长(学习率)为α,即可得到一次迭代后的坐标值x1:
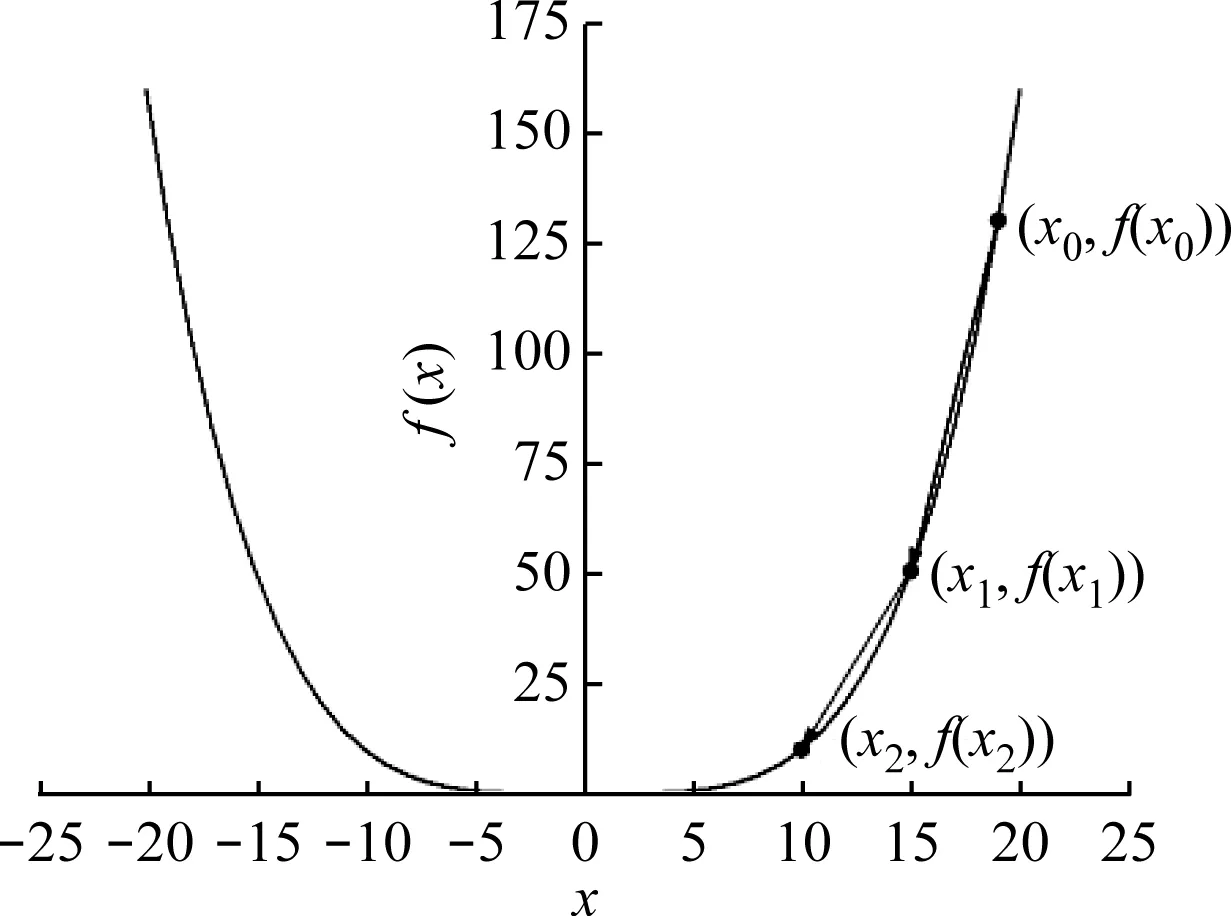
图4 梯度下降法示意图
x1=x0-α(f(x0)-f(x1))
(1)
若此时计算得到的目标函数值f(x1)未达到阈值,则进行下一次迭代,并将坐标(x1,f(x1))作为该次迭代的起点;依此类推,直至损失函数L(x)的值小于阈值λ或达到规定的迭代步数时,终止迭代,并认为此时目标函数f(x)的梯度下降达到了极值。
2.2 1/4电桥应变响应的旋转试验
由于车辆在实际运行过程中,轮对呈周期性转动,故轮对曲辐板上任意位置处的应变响应应为随时间变化的周期函数。为方便试验中各测量半径处应变结果的拾取,本文采用等价测量的方式,即某一时刻同一测量半径下应变随圆周的空间分布曲线,可等价视为该测量半径下某一点处应变随时间的变化曲线[8]。基于此等价测量的方式,进行了1/4电桥应变响应的旋转试验。在试验中,对轮对分别施加FV=70 kN、FT=30 kN,并同时对轮对施加转速n=10 r/min,以近似模拟轮对在车辆运行中的实际滚动状态。
由于在本试验中,需要对轮对进行动态加载,而传统的测力轮对标定试验台只能对轮对施加静态荷载[9-10]。本文采用测力轮对标定试验台(见图5),在实现垂向力与横向力独立或联合加载功能的前提下,可对轮对施加最大转速n=10 r/min,从而实现对测力轮对的动态标定。

图5 测力轮对标定试验台
根据第2.1节中确定的最优组桥半径,即横向组桥半径RT为170 mm,垂向组桥半径RV为300 mm,在1/4电桥应变响应的旋转试验中记录了上述最优组桥半径处的应变随时间的变化曲线,其响应结果如图6—图7所示。

图6 垂向力电桥旋转应变-时间关系曲线

图7 横向力电桥旋转应变-时间关系曲线
由图6—图7可知,通过曲辐板横向力电桥及垂向力电桥测得的应变随时间的变化曲线均呈现良好的周期性。因此,本文认为,当选取应变-时间关系曲线上同一角度、不同时间处的应变时,即可近似模拟轮对在同一时刻不同角度处的应变,并可通过分析得到轮对的最优组桥角度。
2.3 组桥角度优化
根据梯度下降法以及1/4电桥应变响应的旋转试验中获得的应变周期曲线,通过对称组桥和正交双桥组合的方式对连续测量法测力轮对的应变片布置角度进行优化。具体的优化方案为:在测力轮对曲辐板的同一半径处布置两个惠斯通电桥,分别记为A桥和B桥,两个惠斯通电桥的相位差为90°;同一电桥内利用对称组桥的方式组桥,即将应变片关于曲辐板圆心呈中心对称布置,并将对称的两枚应变片作为1组,布置于惠斯通电桥的邻桥位置。
在完全消除高阶谐波影响的理想状态下,两个惠斯通电桥的输出结果为只包含一阶谐波的正弦波形或余弦波形。因此,拾取A、B两个电桥的输出应变εA和εB,将其取平方和后再取算术平方根,得到的电桥应变εi(i=1,2,…,n)应大小恒定,其图像应为一条水平直线。然而在实测数据中,由于系统误差等因素的存在,SRSS(平方和开平方根)较难表现为一条完美的水平直线,但其平滑程度与构成其数据间的离散程度相关。因此,为评价测力轮对的测量精度,引入平均误差θ的概念。θ的计算式为:
(2)
式中:
n——电桥应变点的总数。
利用梯度下降法,分别对图6和图7中所示的应变曲线结果进行迭代。设定迭代次数为10 000次,学习率α为0.1°。对比不同贴片数量的组桥方案中获得的θ,从而得到横向力电桥与垂向力电桥的最优布置角度和最优贴片数量。图8显示横向力、垂向力电桥输出波形θ-应变片数量关系曲线。

图8 横向力、垂向力电桥输出波形θ-应变片数量关系曲线
由图8可知:横向力电桥与垂向力电桥的θ均随应变片数量的增加而逐渐减小;当应变片数量为7组时,横向力电桥组桥输出波形的最小平均误差θmin为0.918%,垂向力电桥组桥输出波形的θmin为0.822%。此时,横向力电桥与垂向力电桥组桥的应变-时间关系曲线如图9和图10所示。
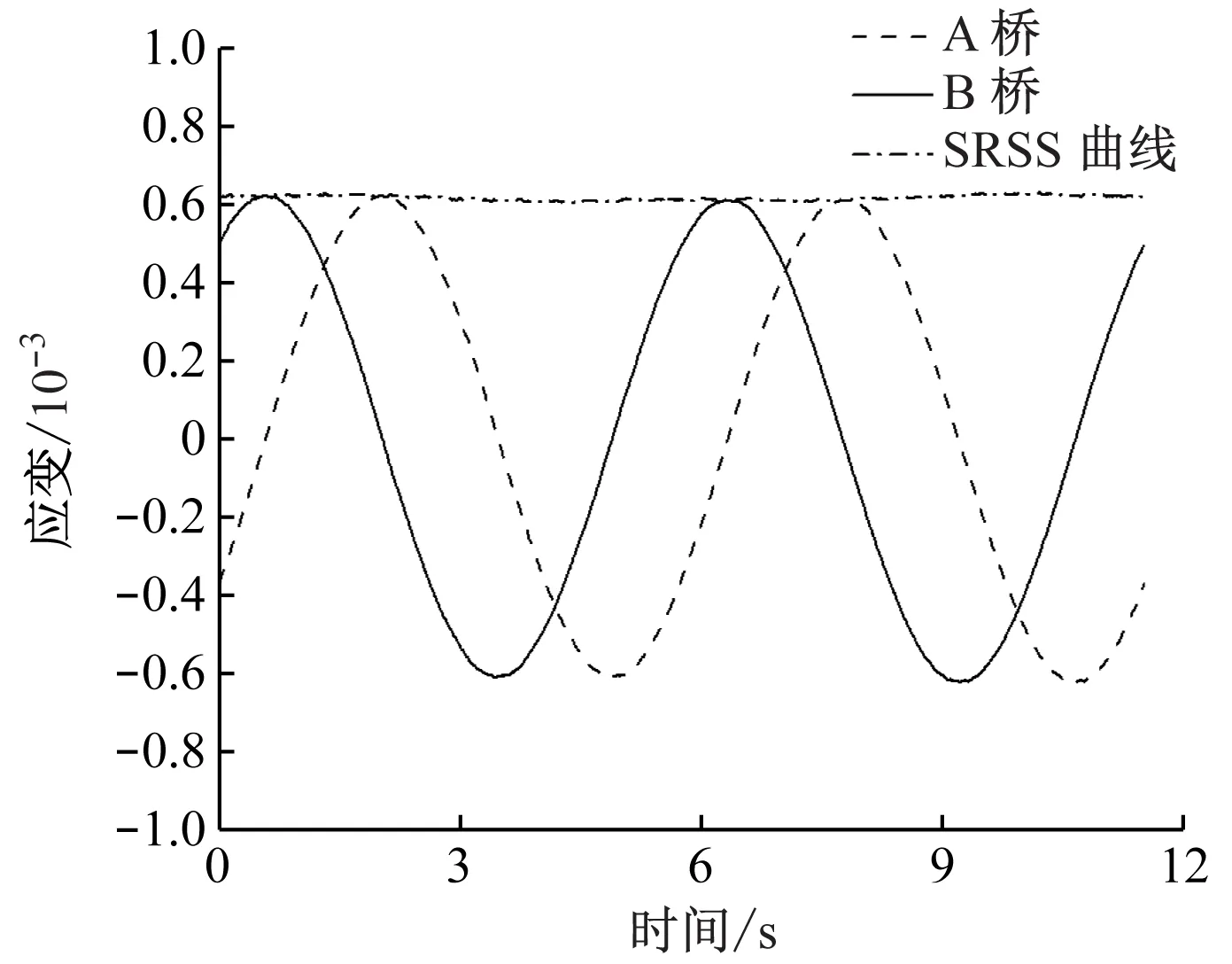
图9 横向力电桥组桥的应变-时间关系曲线

图10 垂向力电桥组桥的应变-时间关系曲线
单个电桥由7组轴对称应变片组成时,所得θ已足够小,精度已满足试验需求。因此,选定组成单个电桥的轴对称应变片组数为7组。
2.4 测力轮对组桥试验研究
在得到最优贴片角度的基础上,对曲辐板测力轮对进行组桥试验。测力轮对贴片布线如图11所示。

图11 测力轮对贴片布线图
在测力轮对标定试验台上对测力轮对进行动态加载试验。动态加载试验包括横向单独加载和垂向单独加载。对测力轮对分别单独施加FT=20 kN和FV=40 kN,并给轮对提供200°/min的转速,共旋转360°,总时长为108 s,采样频率为50 Hz,从而得到FV与FT的SRSS曲线。将SRSS值乘以标定系数后与在标定试验台上施加的力进行对比。测力轮对实测与实加的FT与FV时程曲线如图12和图13所示。

图12 测力轮对实测与实加FT时程曲线

图13 测力轮对实测与实加FV时程曲线
采用θ对测力轮对轮轨力的测量精度进行评价。θ的计算式为:
(3)
式中:
F实测,i——实测的轮轨力;
F实加,i——通过标定试验台获取的轮轨力。
通过计算可知:通过标定试验台对测力轮对施加横向力时,其获取的轮轨力与实测轮轨力的θ为1.27%;通过标定试验台对测力轮对施加垂向力时,上述两者的θ为3.81%。由此可见,两者整体上吻合良好,说明优化组桥方案具备良好的准确性与可行性。
3 结论
1) 在横向力电桥应变片粘贴半径为170 mm,垂向力电桥应变片粘贴半径为300 mm时,两者耦合作用最小,因此,这两个半径为测力轮对最佳应变片粘贴半径。
2) 本文共计算了4~7组应变片的组桥工况,并对比了不同工况下按最佳贴片角度组桥输出的SRSS波形的平均误差。当组桥的应变片组数为7组时,横向力电桥与垂向力电桥输出SRSS波形的方差均为最小。横向力电桥组桥输出波形的θmin为0.918%,垂向力电桥组桥输出波形的θmin为0.822%。输出的SRSS波形较为平稳,故横向力电桥与垂向力电桥均采用7组应变片的组桥方式。
3) 对实测轮轨力与通过标定试验台获取的轮轨力进行比较发现,两者吻合良好,其中:通过标定试验台对测力轮对施加横向力时,其获取的轮轨力与实测轮轨力的θ为1.27%;通过标定试验台对测力轮对施加垂向力时,上述两者的θ为3.81%。,因此优化组桥方案下测力轮对具有较高的精度。
