冻融循环对黄土剪切屈服与破坏行为的影响
2023-11-06邵生俊王松鹤刘乃飞王永鑫
郑 方,邵生俊,王松鹤,刘乃飞,王永鑫
(1.西安建筑科技大学 土木工程学院,陕西 西安 710055;2.西安理工大学 土木建筑工程学院,陕西 西安 710048;3.南昌工程学院 土木与建筑工程学院,江西 南昌 330099)
在我国西北部的基础设施建设和环境保护工程中,涉及到的许多岩土工程问题都与黄土的工程特性密切相关.而黄土广泛分布的大部分地区又属于干旱、半干旱的季节性冻土区,这些黄土工程在建设和运行过程中又会受到冻融循环的影响,冻融循环可能会引发黄土地质灾害或岩土工程问题,尤其是在春季解冻期间[1-6].因此,探索研究冻融循环对黄土力学行为的影响是很有必要的.
关于冻融循环对黄土力学特性的影响,国内外学者通过不同的试验方式进行了大量的研究,例如胡再强等[7]、张玲玲等[8]分别基于常规三轴试验研究了冻融循环作用对不同地区黄土的强度特性的影响.Xu等[9]通过常规三轴试验研究了冻融循环作用对含盐黄土剪切强度的影响.宋春霞[10]、董晓宏等[11]、李丽等[12]都是利用直剪试验来研究干湿和冻融循环对黄土抗剪强度特性的影响.周志军等[13]等利用单轴固结、直剪试验研究了冻融循环对黄土路用性能的影响.倪万魁等[14]利用单轴压缩和三轴剪切试验研究了冻融循环对原状黄土和重塑黄土的抗剪强度的影响.许健等[15]等利用直剪试验研究了重塑黄土在冻融过程中黏聚强度的变化规律.但这些研究多是基于常规三轴试验、单轴试验、直剪试验等常规试验进行的,但事实上在实际工程中土体的受力更为复杂,常规试验所能反映的应力路径有限.
虽然也有少数学者开始利用平面应变试验[16]、真三轴试验进行[17]冻融循环作用对黄土力学行为影响的试验研究,由在常规应力路径下冻融循环作用的研究逐步发展到多种复杂应力路径下的研究,但是目前对于在复杂应力路径下冻融循环对黄土力学行为的研究进行得还较少,目前还处于一个探索阶段,而且多是限于对其应力应变、强度特性的研究,而对于复杂应力路径下冻融循环对黄土剪切屈服和破坏特性的研究更少.一般根据屈服状态和破坏状态下的应力、应变发展水平不同,将岩土材料受荷后弹性变形和塑性变形的临界状态定义为屈服状态,而应力水平保持不变但变形持续发生塑性流动的状态定义为破坏状态[18-20].对于土体屈服状态的判别不同学者给出不同的判定方法,Jardine[21]以0.04%以内的应变为标准.Prashant等[22]以应变能和应力矢量长度间关系曲线双线性化后的交叉点为屈服点.周小文等[23]以归一化的刚度与轴向应变双对数后关系曲线的转折点为屈服点.张玉等[24]以小主应变与轴向应变间关系曲线切线的交点为屈服点.王智[25]以应力比与轴向应变间关系曲线的切线交点为屈服点.
因此,本文基于不同冻融循作用下黄土的真三轴剪切试验结果,研究了在三维应力作用下冻融循环对黄土初始剪切屈服特性和破坏特性的影响,对屈服应变、屈服应力、破坏应力随冻融循环和中主应力的变化进行分析,并对不同冻融循环作用下破坏准则的适用性进行探讨,为冻融作用引发的黄土工程灾害提供理论基础.
1 试验材料及方案
1.1 试验土样
试验用土取自西安市东郊某地,取土深度为3~5 m,根据《土工试验方法标准》(GB/T50123—2019)测得试验用土的基本物理性质参数见表1.参考文献[14]的真三轴试样制备方法,制备含水率为18.6%,干密度为1.5 g/cm3,尺寸为7.0 cm×7.0 cm×14.0 cm的立方体重塑黄土试样.

表1 试验用土的基本物理性质参数
1.2 试验仪器
本次试验采用的是一向刚性加载,两向柔性加载的刚柔复合型真三轴试验仪,如图1所示.该仪器主要包括:(1)压力室;(2)液压囊;(3)轴向及侧向应力加载系统;(4)变形量测系统;(5)水-气控制系统等几个部分.该仪器可以实现对试样进行三向独立加载,互不干扰,更加真实地模拟土体在实际工程中可能受到的非对称受力情况.

图1 真三轴试验仪
1.3 试验方案
将制备好的真三轴试样密封在塑料袋内,然后将试样放置在恒温箱内,通过调节恒温箱的温度,使试样经历冻融循环作用.先设置恒温箱温度为-20°(12 h)使试样冷冻,然后设置温度为20°(12 h)使试样融化,此为一次冻融循环.本次试验设计冻融循环次数N分别为N=0,N=1,N=3,N=5,N=10.
对经历不同冻融循环后的试样分别进行固结排水真三轴剪切试验,加载应力路径采用等b等p剪切路径,如图2所示.设定中主应力参数b=0,0.25,0.5,0.75,1,球应力p=300 kPa.剪切时采用应变控制方式,剪切速率为0.05 mm/min,剪切试验的终止条件为轴向应变达到15%.
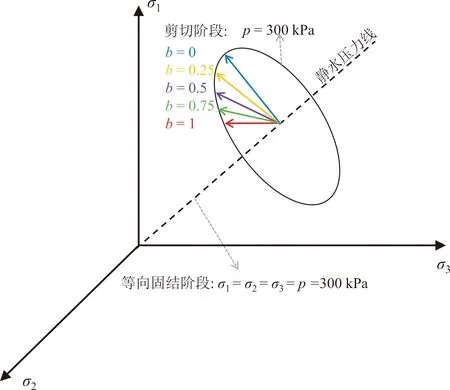
图2 剪切路径
2 试验结果分析
为了以下叙述方便,对涉及到符号在此进行说明:
中主应力参数,b
(1)
球应力,p
(2)
广义剪应力,qs
(3)
广义剪应变,εs
(4)
应力比,η
(5)
2.1 试验结果
图3给出广义剪应变εs与应力比η的关系曲线,可以看出不同中主参数条件下,应力比η呈现出相似的变化规律,随着冻融循环次数的增加,应力比η先减小后又增大后趋于稳定,未经历冻融循环的土样的应力比η始终最大.这一现象主要是由于冻融循环过程中土体内部孔隙结构发生了变化.由于孔隙中水分的冻结,土孔隙变大,而不是所有的孔隙在冰融化后都能完全恢复到初始状态.因此,土体结构趋向于变得相对松散,导致土体强度降低,应力比减小.经过多次冻融循环,土体结构达到一个新的平衡,对应一个基本恒定的土体强度,应力比也趋于稳定.对比不同b下的广义剪应变εs与应力比η的关系曲线,可以看出随着b值从0变化到1,同一冻融循环下应力比η逐渐减小,且随着b值的增大,不同冻融循环间应力比η的差值逐渐减小.

图3 广义剪应变随应力比的变化
2.2 屈服特性
参考文献[22-25],随着真三轴剪切过程的持续发展,广义剪应变εs与应力比η的关系曲线有明显的转折点,通过分别做出εs~η关系曲线首、尾两部分的切线,两条切线的交点可作为试样的屈服点,如图4所示,交点所对应的应变和应力比可作为屈服应变(εy)和屈服应力比(ηy).
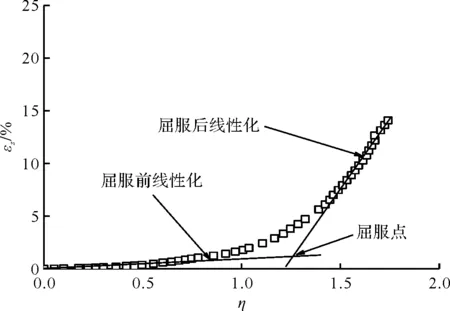
图4 屈服点的确定示意图
根据图4确定出,不同冻融循环作用下不同中主应力参数下试验测试结果的屈服点,得到屈服点的屈服应变(εy)和屈服应力比(ηy).图5给出屈服应力比随冻融循环作用的变化曲线,可以看出不同中主应力参数的屈服应力比随冻融循环次数的变化规律基本一致,呈现出先减小后增大而后又趋于稳定的变化趋势,且b=0时的屈服应力比ηy与其他b值的屈服应力比ηy差值较大.
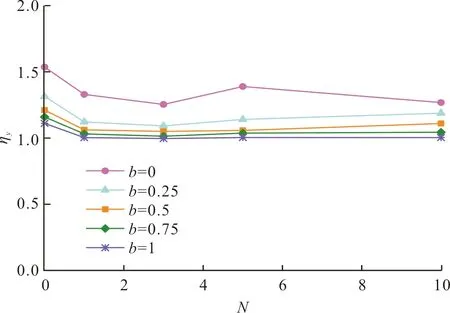
图5 屈服应力比随冻融循环次数的变化
图6给出屈服应力比ηy随中主应力参数b的变化曲线,可以看出不同冻融循环作用下屈服应力ηy比随中主应力参数b的变化规律基本一致,随着b的增大都呈现出减小的趋势,且N=0时屈服应力比ηy与其他冻融循环作用下的屈服应力比ηy差值较大.图7给出屈服应变εy随冻融循环作用的变化曲线,可以看出不同中主应力参数b的屈服应变εy随冻融循环次数的变化规律基本一致,大致呈现出先减小后增大后又减小而后趋于稳定的变化趋势.图8给出屈服应变εy随中主应力参数b的变化曲线,屈服应变εy随b没有呈现出明显的变化规律,屈服应变εy大致分布在0.3%到1.6%之间.

图6 屈服应力比随b的变化
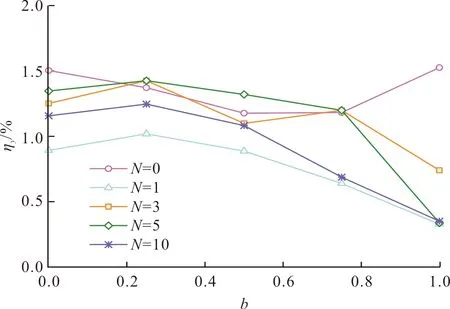
图8 屈服应变随b的变化
2.3 屈服应力与破坏应力的对比
定义试样破坏点为轴向应变ε1达到15%所对应的点,该点对应的剪切应力为破坏应力qf,图9、图10分别给出屈服应力qy、破坏应力qf随b的变化曲线,可以看出不同冻融循环次数下的屈服应力qy、破坏应力qf随着b值的增大呈现出基本一致的变化规律,都是随着b值的变化而逐渐减小的.图11、图12分别给出屈服应力qy、破坏应力qf随冻融循环次数N的变化曲线,可以看出不同b值下的屈服应力qy、破坏应力qf随着b值的增减呈现出基本一致的变化规律,都是随着冻融循环次数N先减小后又增大而后又趋于稳定.

图9 屈服应力随b的变化
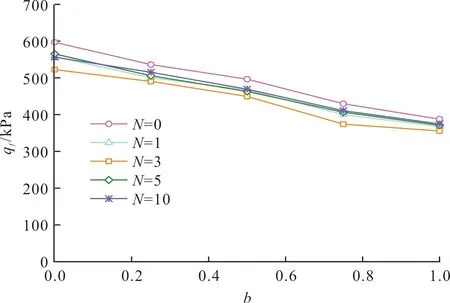
图10 破坏应力随b的变化
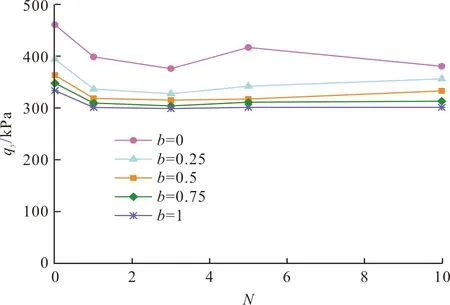
图11 屈服应力随冻融循环次数的变化

图12 破坏应力随冻融循环次数的变化
图13给出在π平面上不同冻融循环次数的屈服应力点、破坏应力点,可以看出屈服应力均小于破坏应力,不同冻融循化下的屈服应力点的轨迹形状相似,破坏应力点的轨迹相似,屈服点应力点的轨迹与破坏应力点的轨迹不同.

图13 π平面上的屈服应力和破坏应力的比较
2.4 破坏准则的适用性分析
图14给出π平面上试验测试所得的不同冻融循作用下的破坏点应力及广义Mises准则、Lade准则、M-C准则(Mohr-Coulomb准则)的预测破坏轨迹,可以看出冻融循环作用对π平面上试样的破坏轨迹形状的影响不明显,不同冻融循环作用下试验结果测试所得的结果基本一致,破坏点的破坏应力都与Lade准则预测的破坏轨迹较接近,而广义Mises准则的预测结果偏大,M-C准则的预测结果偏小,分析原因为广义Mises准则中假定中主应力σ2与小主应力σ3的作用是相等的,而M-C准则中未考虑中主应力σ2的作用。
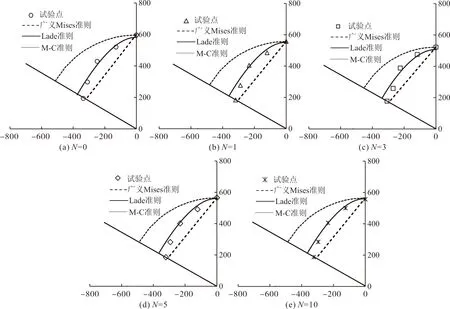
图14 π平面上的破坏准则分析
3 结论
本文基于不同冻融循环作用下不同中主应力条件的黄土真三轴剪切试验,探讨了在复杂应力路径下冻融循环作用对黄土剪切屈服与破坏行为的影响,得到的主要结论如下:
(1)随着冻融循环次数的增加,应力比先减小后增大后又趋于稳定,随着b值的增大,应力比逐渐减小,且应力比的差值逐渐减小;
(2)屈服应力比、屈服应力、破坏应力都随着冻融循环次数的增加先减小后又增大后又趋于稳定,随着b值的增加逐渐减小;
(3)屈服应力均小于破坏应力,π平面上屈服应力点的轨迹与破坏应力点的轨迹不同,但不同冻融循环作用下的屈服应力点轨迹、破坏应力点轨迹基本相似;
(4)不同冻融循环下破坏点应力与广义Mises准则、Lade准则、M-C准则的预测破坏轨迹相比较,Lade准则与破坏应力点的轨迹较为一致,且破坏轨迹的形状受冻融循环作用的影响不大.
