改进的L1/2阈值迭代高分辨率SAR成像算法
2023-11-06高志奇孙书辰黄平平乞耀龙
高志奇 孙书辰 黄平平* 乞耀龙 徐 伟
①(内蒙古工业大学信息工程学院 呼和浩特 010080)
②(内蒙古自治区雷达技术与应用重点实验室 呼和浩特 010051)
1 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种全天候、全天时微波遥感成像雷达,有着广泛的应用前景和发展潜力。SAR通过发射大带宽的电磁波信号,经过脉冲压缩实现高距离向分辨率,在方位向通过与成像区域的相对运动形成一个大的虚拟孔径,采用合成孔径原理提高方位向分辨率。由于SAR在成像领域独有的优越性,世界各国都在大力发展SAR技术及其成像算法。但SAR在实际工作中会受到各种外界的干扰,从而造成回波数据的缺失,影响SAR成像的分辨率[1]。现有研究表明,可以将SAR回波数据缺失等效为稀疏采样,借助相关方法提高其成像分辨率,具有重要的应用价值和实际意义。
2006年,由Donoho[2]提出的压缩感知(Compressive Sensing,CS)理论表明,如果信号可压缩或在某个变换域是稀疏的,则可以在远低于奈奎斯特采样率的情况下精确重构原始信号。CS理论利用信号的稀疏性进行压缩采样处理,然后求解一个非线性约束最优化问题,利用稀疏重构算法对其进行恢复。信号的带宽与重建信号所需的采样率不直接相关联,从而可以大幅降低采样率。在稀疏场景下,雷达回波信号通常可以看作测绘带少数强散射点回波信号的叠加,具备稀疏性质,因此可以将CS理论应用到SAR成像领域[3–6]。
文献[7,8]将SAR原始回波数据进行距离向压缩和徙动校正之后,通过在每个距离门上构建方位向观测矩阵,利用稀疏重构方法重建图像。文献[9]提出,当SAR回波数据量较小时,利用L1/2范数约束优化的重建算法可以重构图像。文献[10]提出在SAR非均匀采样条件下选用正交匹配跟踪算法(Orthogonal Matching Pursuit,OMP)遍历所有距离单元,可以得到全场景的方位向压缩结果,并且能够实现目标的低旁瓣、高分辨率成像。文献[11]针对条带模式SAR,提出将条带数据分块为多个子孔径数据,对子孔径利用CS恢复缺失数据,拼接得到整个条带数据,缩短了整个数据的恢复时间。
上述方法无论对距离门的遍历,还是划分子孔径拼接成像,都不是直接基于原始数据成像,需要在距离向压缩和距离徙动校正之后,采用稀疏信号处理方法进行方位向压缩,不仅不能降低系统的复杂度和采样率,反而增加了信号处理的复杂性。为了解决上述问题,文献[12]提出基于近似观测的CSSAR成像模型,采用了加权L1正则化项的稀疏约束;文献[13]提出基于L1/2正则化理论的稀疏雷达成像,利用SAR回波模拟算子实现稀疏雷达信号重构;文献[14,15]针对SAR回波数据方位向任意缺失部分数据下的成像问题,通过改进迭代阈值算法(Iterative Shrinkage Thresholding,IST)有效减少重建误差,提高了SAR成像质量。
近年来,压缩感知重构算法是应用数学、信号处理等研究领域的热点问题。其中,IST算法作为一种求解反问题的优化方法,因其与多尺度几何分析存在紧密联系,且具有算法参数少、实现过程比较简单等特点,已经得到了广泛应用。然而文献[16,17]指出IST算法的收敛速度慢,不适合实时性要求高的场景。基于此,文献[18]提出了加速IST算法:两步迭代阈值算法(Two-step Iterative Shrinkage Thresholding,TwIST);文献[19]提出了一种Nestrerov加速算子;文献[20]将Nestrerov加速算子结合IST提出快速迭代阈值算法(Fast Iterative Shrinkage Thresholding,FIST);文献[21]修改了IST算法表达式中的梯度算子,在每一步迭代的过程中,重构图像的求解同时依赖前两步的迭代,得到改进的迭代软阈值算法(Iterative Soft Thresholding Algorithm,ISTA),并通过实验证明在加速IST算法的同时也提高了最优解的稀疏度。上述算法都是基于L1正则化理论,针对一维信号可以获得较高的重构精度,但对于二维图像,由于其使用时域的软硬阈值算子,不能获得很好的图像稀疏表示,算法重构精度不高。文献[22–25]发现凸松弛的L1正则化并不能产生足够稀疏的解,提出L1/2正则化理论,并证明L1/2正则化比L1正则化能产生更加稀疏的解,即L1/2正则化能够更加精确地重构原始信号。
本文针对SAR在稀疏采样条件下,方位向分辨率低、现有稀疏成像算法速度慢等问题展开研究,将SAR近似观测模型与L1/2阈值迭代过程结合,提出改进的L1/2阈值迭代算法,通过稀疏重构的方式提升目标成像的聚焦性,改善方位向分辨率。从原始数据域出发采用SAR近似观测模型[26,27],将成像算子代替观测矩阵及其共轭转置,可以使内存的消耗从场景尺寸的平方阶降低至线性阶,同时基于频域匹配滤波的快速成像算法可以将计算量从场景尺寸的平方阶降低至线性对数阶,大大降低了对数据处理器硬件系统性能的要求,同时也降低了计算量。本文分别在全采样和欠采样的条件下进行点目标仿真实验,结果证明了改进算法相比于传统的Chrip-Scaling算法、L1/2阈值迭代算法在SAR成像分辨率方面有了一定的改善,同时在算法收敛速度方面也有所提高。最后通过实测数据处理实验证明了本文所提算法成像的有效性。
2 基于近似观测的SAR成像模型
本文主要研究正侧视下的条带式SAR成像,其模型如图1所示。SAR距离向的分辨率是通过发射线性调频(Linear Frequency Modulated,LFM)信号来实现的,方位向采用合成孔径工作原理和相干叠加成像方法来提高分辨率。
当机载雷达处于复杂工作环境时,可能会造成部分SAR回波信号数据缺失,导致传统成像方法性能下降。现有研究表明,CS-SAR成像方法不仅适用于满采样SAR回波数据提高成像质量,而且在稀疏场景中还适用于欠采样SAR回波数据的无模糊成像。然而,SAR原始数据在方位向和距离向具有耦合性,直接构建观测矩阵进行稀疏重构,需将二维满采样回波矩阵重新排列为一维向量,当观测场景的空间尺度较大时,利用观测矩阵进行稀疏重构将消耗海量内存。基于近似观测模型的CS-SAR成像算法可以直接面向二维原始回波信号进行成像,有效解决上述难题。
本文以Chirp-Scaling回波模拟算子构建近似观测模型。Chirp-Scaling SAR成像算法的主要步骤包括:首先在距离多普勒域通过第1次相位相乘实现Chirp-Scaling操作,使所有目标的距离徙动轨迹一致化;然后在二维频域通过与参考函数进行第2次相位相乘完成距离压缩和一致距离徙动校正;最后在距离多普勒域与随距离变化的匹配滤波器进行第3次相位相乘完成方位向压缩。
基于Chirp-Scaling算法的成像算子可以表示为[12]
其中,Y表示SAR原始二维回波数据;Fr和Fa分别表示距离向和方位向傅里叶变换;分别表示距离向和方位向傅里叶逆变换;Qsc表示Chirp-Scaling解耦算子;Qac表示方位压缩及相位校正;Qrc表示距离压缩和一致距离徙动校正;⊙表示Hadamard乘积;ICS:CM×N →CM×N符号是成像算子,M表示方位向采样点数,N表示距离向采样点数。
Qsc表达式如下:
其中,D(fh,vr)表示二维频域中的徙动因子,fh表示方位向频率,vr表示飞机相对于地面的速度,t与t2分别表示不同的相位中心,Ks表示调频率。
Qac表达式如下:
其中,ft表示距离向频率,Rref表示参考距离,c表示光速,Cs表示调制系数。
Qrc表达式如下:
其中,Rs表示目标和雷达的最短斜距,θ表示残留相位。
由于成像算子ICS(Y)中的矩阵或算符之间的操作都是由矩阵乘法和矩阵Hadamard乘法构成的,所有算符都是线性的,因此推导可以得到其逆成像算子GCS(X)的表达式如下[12]:
其中,X为观测场景的二维复数图像数据;(⋅)*表示矩阵共轭操作;GCS:CM×N →CM×N符号是近似观测算子。
成像算子ICS和近似观测算子GCS两者的关系可以描述为[12]
其中,(⋅)H表示矩阵共轭转置。
基于近似观测模型的CS-SAR成像重构过程可以通过求解如下形式的线性方程来实现:
为了获得观测场景的二维复数图像X,可以利用凸松弛理论,将其转化基于近似观测模型的L1正则化问题:
其中,λ>0为正则化参数。
通过求解式(8)可以得到观测场景的二维图像。
3 改进的L1/2阈值迭代算法
3.1 L1/2阈值迭代算法
随着压缩感知技术的不断发展,越来越多的研究结果表明,L1范数约束往往并不能保证产生最稀疏的解,也不能在较少的采样率下精确恢复原始信号。针对其存在的问题,文献[22-25]研究了如式(9)所示的Lq正则化问题。
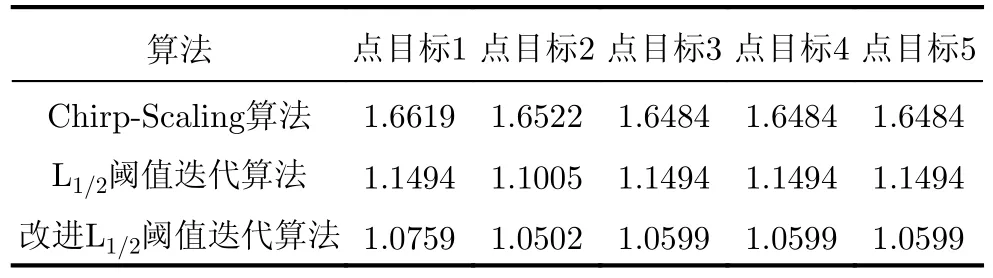
研究结果表明,当q∈(0,1/2]时,Lq正则化性能没有明显差异;当q∈(1/2,1]时,Lq正则化性能递减。经过一系列严格的数学分析得出结论,q=1/2是Lq(0 基于L1/2阈值迭代算法的一般表达式为 其中,µ为用来控制梯度下降算法收敛速度的参量,;Hλ,µ,1/2表示阈值算子,其具体表达形式为 其中,N代表N×1的矩阵, 从式(10)可以看出,基于L1/2阈值迭代算法仅仅只是梯度下降法的一种扩展,对于每次迭代只利用了当前点的信息进行梯度估计。 为提高式(9)的迭代收敛速度,文献[19]提出一种Nestrerov加速算子,文献[20]将其与IST算法结合,在加快算法收敛的同时,提高解的稀疏度,其迭代计算步骤如下: 步骤1 设置迭代步长 步骤2 引入加速算子 步骤3 用ξn+1代替式(10)中的得到其迭代算法的一般表达式: 该迭代过程在计算下一步迭代点Xn+1时不仅依赖上一步迭代点Xn,还依赖更前一次的迭代点Xn-1。 受上述方法的启发,文献[21]计算函数在Xn处的梯度∇f(Xn),在原表达式中减去前一次迭代点Xn-1的一个算子,从而得到新的梯度算子∇g(Xn)为 其中,I表示单位矩阵,参数α>0。从而得到改进的迭代软阈值算法对应的一般表达式: 基于上述原理,本文提出改进的L1/2阈值迭代算法,其迭代步骤具体如下: 其中,n=0,1,⋅⋅⋅,N。 本文将改进的L1/2阈值迭代算法与SAR近似观测模型相结合,提出改进的L1/2阈值迭代高分辨率SAR成像算法。该算法的主要过程如下: 输入:原始回波数据Y,初始化二维观测场景复图像X0,v0=0,最大迭代次数Imax。 迭代计算:forn=1:Imax+1 输出:Xn–1 文献[20]通过引入文献[19]中的Nestrerov加速算子对ISTA进行改进,形成FISTA方法;文献[21]在文献[20]中迭代过程的基础上,对ISTA中梯度算子进行改进,形成改进的迭代软阈值算法并通过实验证明了其能以更少的测量数对稀疏信号进行恢复。本文在文献[21]研究结果的基础上,将其所提方法与L1/2正则化理论结合,形成改进的L1/2阈值迭代算法,并结合近似观测模型对SAR回波数据进行处理,以提升成像实时性、分辨率等性能。本文所提算法在稀疏场景中同样适用于欠采样SAR回波数据的高分辨成像。 本节通过设置理想点目标并对其回波数据进行处理,结合SAR实测数据的成像实验,验证本文所提改进L1/2阈值迭代算法相比传统的Chirp-Scaling算法、L1/2阈值迭代算法在改善目标成像分辨率及加快算法收敛速度方面的优势。 首先通过点目标仿真方式生成理想的SAR回波数据,然后将传统的Chirp-Scaling算法、L1/2阈值迭代算法与本文所提改进L1/2阈值迭代算法进行点目标成像聚焦处理,并分别分析各算法成像的实际分辨率,对比3种算法成像的剖面图,从而验证本文所提改进算法在改善目标成像分辨率方面的有效性。仿真实验参数如表1所示。 表1 SAR成像仿真参数Tab.1 Simulation parameters of SAR imaging 点目标布局如图2所示,共有5个点目标分布在条带区域中,每个点目标均具有相同的散射系数,并按照表1所示的仿真参数设置,生成二维SAR回波数据。 图2 点目标位置Fig.2 Point target position 图3是Chirp-Scaling算法的成像结果图,从图中可以明显看出点目标有着丰富的旁瓣。图4为L1/2阈值迭代算法的成像结果,可以看出目标的旁瓣大大减少,目标的能量提高,成像质量显著提升。图5为本文所提改进L1/2阈值迭代算法的成像结果,可以看出点目标的成像质量相比于Chirp-Scaling算法在聚焦效果上有了显著的提升,目标的能量明显提高。 图3 Chirp-Scaling算法成像结果Fig.3 Imaging results of Chirp-Scaling algorithm 图4 L1/2阈值迭代算法成像结果Fig.4 Imaging results of L1/2 threshold iterative algorithm 图5 改进L1/2阈值迭代算法成像结果Fig.5 Imaging results of improved L1/2 threshold iterative algorithm 通过点目标成像剖面图说明所提改进L1/2阈值迭代算法相较其他算法在分辨率方面的优势。 为了比较每个点目标的分辨率,定义分辨率的计算式为 其中,va为载机沿方位向飞行速度,B为方位向带宽。 条带场景区域中点目标1, 2, 3, 4, 5的方位向剖面图如图6所示,通过每个点目标方位向的剖面图可以明显看出,Chirp-Scaling算法重建目标的方位向分辨率最差,旁瓣的收敛速度也最慢;L1/2阈值迭代算法重建目标的方位向分辨率较Chirp-Scaling算法有了大幅提高,其旁瓣收敛速度也更快;改进L1/2阈值迭代算法重建目标的旁瓣收敛速度虽没有L1/2阈值迭代算法快,但其主瓣宽度更窄,因此其方位向分辨率较L1/2阈值迭代算法有所改善。 图6 点目标剖面图Fig.6 Cross section of point targets 为了进一步验证改进的L1/2阈值迭代算法在重建目标方位向分辨率方面的优势,对条带区域场景中的5个点目标方位向分辨率进行了定量分析,结果如表2所示。通过对比可以看出,改进的L1/2阈值迭代算法的方位向分辨率相较于其他两种算法更高,从而验证了本文所提改进算法的优势。 表2 3种算法中5个点目标成像分辨率分析(m)Tab.2 Imaging resolution analysis of five targets in three algorithms (m) 为了进一步证明本文所改进算法的优势,本节通过对SAR回波在方位向分别随机缺失60%和70%的数据条件下进行点目标成像仿真,并分别比较3种算法重建目标的分辨率。 图7(a)和图7(b)是分别在方位向数据随机缺失60%和70%的条件下Chirp-Scaling算法成像结果。图8(a)和图8(b)是分别在方位向数据随机缺失60%和70%的条件下L1/2阈值迭代算法成像结果,可以看出该方法能够消除方位向数据缺失导致的目标模糊。图9(a)和图9(b)是分别在方位向数据随机缺失60%和70%条件下改进L1/2阈值迭代算法成像结果,可以看出点目标的成像质量相比于Chirp-Scaling算法在聚焦效果上有了显著的提升。由此可以证明本文所提改进L1/2阈值迭代算法在方位向数据随机缺失条件下的有效性。 图7 Chirp-Scaling算法成像结果Fig.7 Imaging results of Chirp-Scaling algorithm 图8 L1/2阈值迭代算法成像结果Fig.8 Imaging results of the L1/2 threshold iterative algorithm 图9 改进L1/2阈值迭代算法成像结果Fig.9 Imaging results of the improved L1/2 threshold iterative algorithm 表3和表4分别是在SAR回波数据方位向数据缺失60%和70%的情况下3种算法对条带区域场景中5个点目标的分辨率分析,对比表中的数据可以明显看出,本文所提改进L1/2阈值迭代算法较Chirp-Scaling算法对重建点目标的分辨率有了很大程度的提升,较L1/2阈值迭代算法的点目标分辨率也有一定的改善,因此可以证明本文所提改进算法在成像分辨率方面的优势。 表3 3种算法中方位向数据缺失60%时5个点目标的分辨率(m)Tab.3 The resolution of five targets with 60% azimuth data missed for three algorithms (m) 在本节仿真实验中,对理想点目标的回波信号中加入高斯白噪声,通过设置不同的信噪比来分别验证已有算法和本文所提改进算法的有效性和可靠性。 图10为Chirp-Scaling算法、L1/2阈值迭代算法以及本文所提的改进L1/2阈值迭代算法分别在信噪比为20 dB和–20 dB下的成像结果。从图10(a)和图10(b)可以看出Chirp-Scaling算法在信噪比为–20 dB的情况下,成像效果明显恶化。对比图10(c)和图10(d)可以看出L1/2阈值迭代算法在–20 dB的情况下点目标的成像效果依旧清晰,并且很好地抑制了旁瓣。从图10(e)和图10(f)可以看出本文所提改进L1/2阈值迭代算法在信噪比为–20 dB的情况下依旧能对点目标进行清晰的成像,同样对旁瓣有良好的抑制作用,由此可以验证本文所提改进L1/2阈值迭代算法在低信噪比情况下的有效性。 为了进一步突出近似观测模型的优势,本节分别从空间复杂度和时间复杂度进行分析。假设观测场景的二维复数图像和SAR回波信号的网格单元数为M×N,从空间复杂度的角度分析,基于匹配滤波的SAR成像过程不涉及观测矩阵的建立,故其计算机的内存消耗为M×N。基于精确观测模型的CSSAR成像由于需要将二维满采样回波矩阵重新排列为一维向量,因此其计算机内存消耗为MN×MN。而近似观测模型是对成像场景和原始回波数据的直接处理,不需要存储高维度的观测矩阵,故基于近似观测的CS-SAR成像算法的计算机内存消耗为M×N。从时间复杂度的角度分析,基于匹配滤波的SAR成像算法的成像过程中主要有FFT,IFFT和相位参考函数的相乘,FFT和IFFT的时间复杂度为O(MNlog2MN),相位参考函数的时间复杂度为O(MN)。基于精确观测的CS-SAR成像算法涉及高维度精确的观测矩阵和一维反射系数矩阵相乘,设其最大迭代次数为I,故其时间复杂度为O(IM2N2)。而基于近似观测模型的CS-SAR成像算法相比基于匹配滤波的SAR成像算法多了迭代的过程和阈值操作,其时间复杂度为O(IMN),故其总的时间复杂度为O(IMNlog2MN)。表5所示为不同算法模型的运算量对比。 表5 不同模型的运算量分析Tab.5 Calculation amount analysis of different models 为了验证本文所提改进L1/2阈值迭代算法在加快收敛速度方面的优势,本节在不同的采样率情况下分别用L1/2阈值迭代算法、改进L1/2阈值迭代算法对条带区域场景中5个点目标进行重建,在相同计算机配置(CPU:i5-7200U;主频:2.50 GHz;内存:12.0 GB)条件下,通过仿真实验记录各算法的重建目标时长,结果如表6所示。 表6 不同采样率下两种算法重建点目标耗时时长(s)Tab.6 Time consuming of point target reconstruction by the two algorithms at different sampling rates (s) 表6为当采样率分别为100.0%,75.0%,50.0%,25.0%,12.5%时L1/2阈值迭代算法、改进L1/2阈值迭代算法对条带区域场景中5个点目标重建耗时时长。可以明显看出,在不同采样率下,L1/2阈值迭代算法重建目标的耗时较长,改进L1/2阈值迭代算法重建目标的耗时较短,并且相比L1/2阈值迭代算法目标重建时间分别下降了约46%。因此,当观测场景较大时,本文所提改进L1/2阈值迭代算法可以有效缩短重建目标的时间,提升成像的实时性。 本节通过实测数据对比分析相关成像算法的性能,分别用Chirp-Scaling算法、L1/2阈值迭代算法和改进L1/2阈值迭代算法,对加拿大航天局发射的RADARSAT-1卫星传回的SAR数据进行重建成像。表7所示为RADARSAT-1卫星SAR成像参数。 表7 RADARSAT-1卫星SAR成像参数Tab.7 Parameters of RADARSAT-1 satellite SAR imaging 图11(a)为Chirp-Scaling算法重建结果,图11(b)为L1/2阈值迭代算法重建结果,图11(c)为改进L1/2阈值迭代算法重建结果。可以看出,3种算法均得到了较好的成像效果,能够准确重建稀疏场景中关键的舰船目标。比较而言,改进L1/2阈值迭代算法成像结果对目标的聚焦效果最好,有利于后续的目标检测和参数估计。表8所示为3种算法耗时时长分析,相比L1/2阈值迭代算法,本文所提算法成像实时性更高,具有良好的应用价值。 表8 3种算法实测数据成像耗时时长Tab.8 Time consuming of measured data imaging by the three algorithms 图11 不同算法的重建结果Fig.11 Reconstruction results of different algorithms 传统的CS-SAR成像模型需要将二维满采样回波矩阵和二维待重构图像向量化,当观测场景较大时,利用观测矩阵进行稀疏重构将消耗海量内存,不利于实时成像。为了降低成像时数据处理器的压力,将基于近似观测的CS-SAR成像模型应用于成像过程。本文结合近似观测模型,在L1/2正则化理论的基础上改进了阈值表达式中的梯度算子,以提升稀疏成像算法的性能。理论分析和实验验证表明,相比Chirp-Scaling算法和L1/2阈值迭代算法,所提改进L1/2阈值迭代算法在成像分辨率方面有一定的改善,其收敛速度比L1/2阈值迭代算法有了较大提高,可以在稀疏场景且方位向有数据随机丢失的情况下对强目标实现快速高分辨成像。3.2 改进L1/2阈值迭代算法
4 实验与结果分析
4.1 全孔径条件下点目标仿真实验
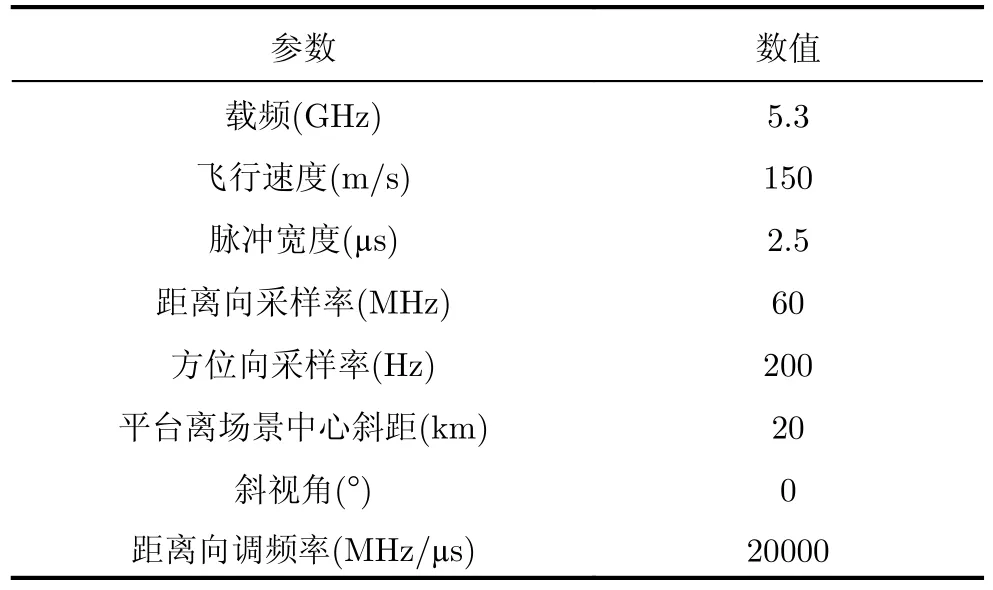
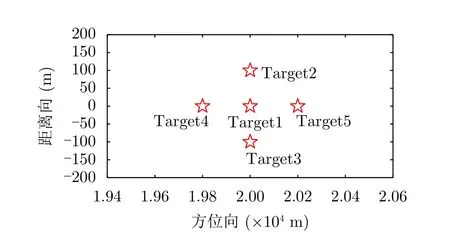
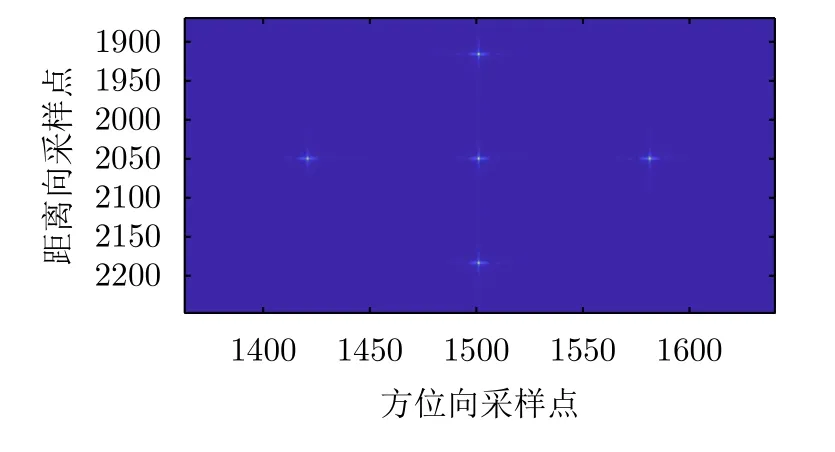
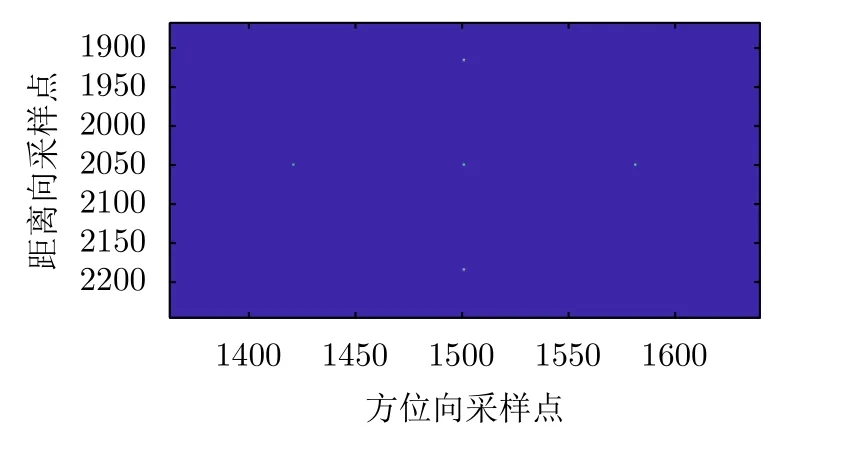
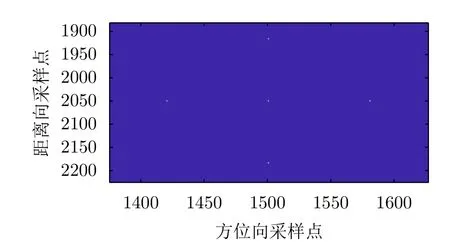
4.2 点目标成像剖面图分析
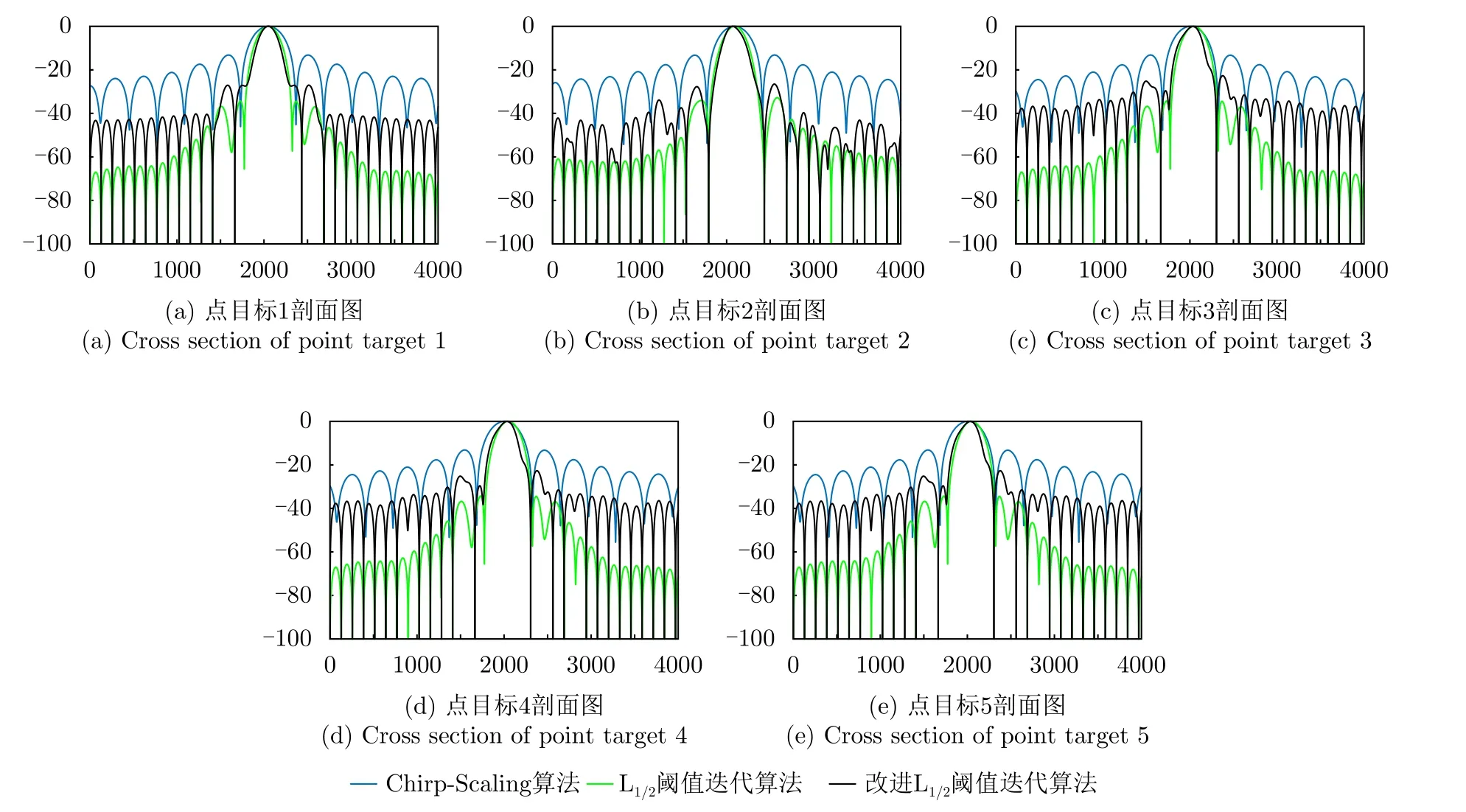
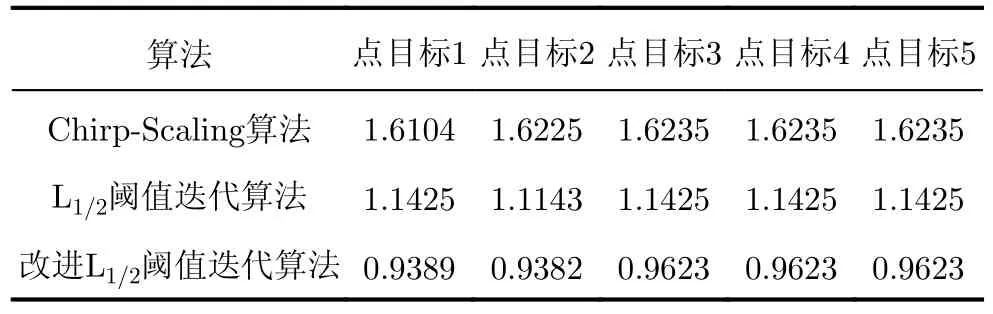
4.3 方位向缺失数据条件下点目标仿真实验
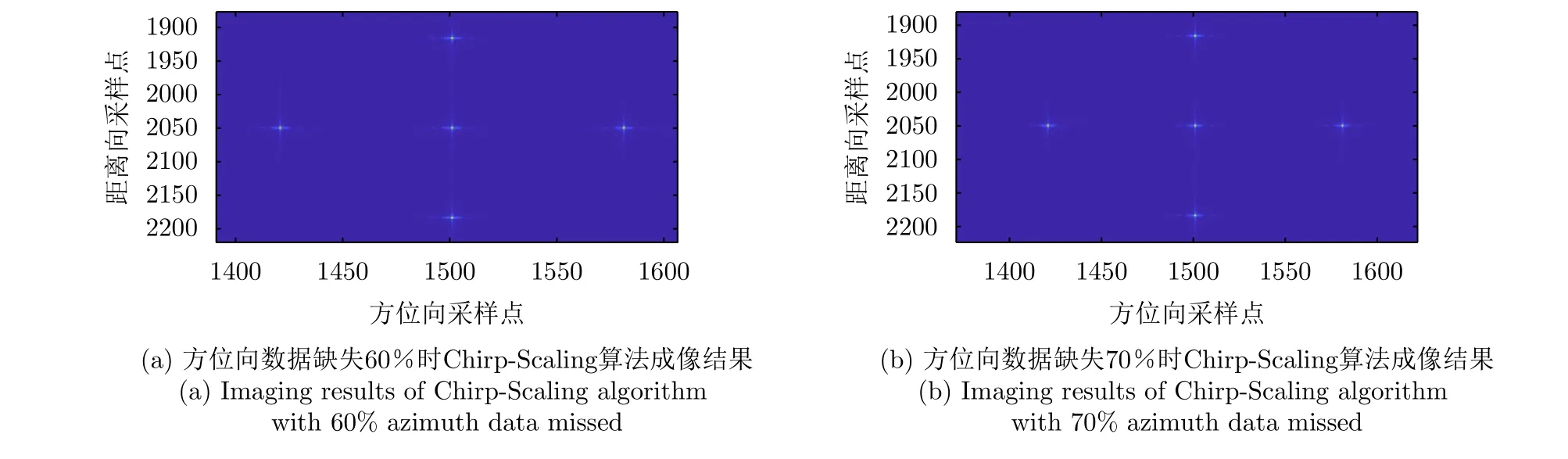
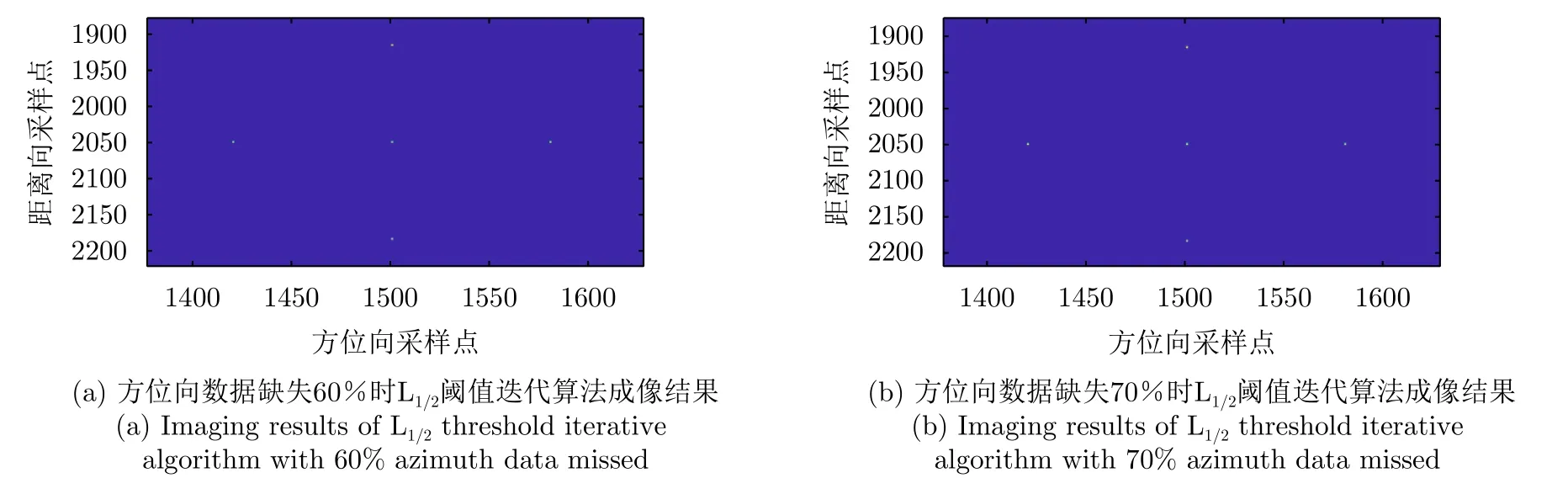
4.4 不同信噪比下的点目标成像仿真实验
4.5 不同算法运算量分析


4.6 实测数据处理实验



5 结语
