基于RD-ANM的毫米波雷达动目标超分辨DOA估计方法
2023-11-06傅东宁陈展野张彦君谭晓衡
舒 月 傅东宁 陈展野* 黄 岩 张彦君 谭晓衡 陶 俊
①(重庆大学微电子与通信工程学院 重庆 400044)
②(北京华力创通科技股份有限公司 北京 100193)
③(华力创通-北方工大雷达射频仿真联合实验室 北京 100144)
④(东南大学信息科学与工程学院毫米波国家重点实验室 南京 210096)
⑤(东南大学信息科学与工程学院水声信号处理教育部重点实验室 南京 210096)
1 引言
车载雷达旨在实时获取全面准确的路况和环境信息,辅助驾驶人员做出决策和保障行车安全[1]。毫米波雷达(Millimeter-wave Radar,MMW Radar)由于工作频率高,分辨率高,体积小,且环境适应性好,兼具高性能和低成本,常被视为汽车主动安全领域的核心部件之一[2]。目前,车载毫米波雷达的研究热点主要集中于4D (Four Dimensions)成像,对目标距离-多普勒-方位角-俯仰角的多维高分辨率精确测量的需求日益增长[3]。为满足目标波达方位角(Direction of Arrival,DOA)估计精度和角度分辨率的高性能需求,且考虑到实际系统设计成本及实现,车载毫米波雷达常采用时分复用-多输入多输出(Time Division Multiplexing-Multiple Input Multiple Output,TDM-MIMO)体制,通过发射线性调频连续波(Linear Frequency Modulation Continuous Wave,LFMCW) 信号,在接收端进行通道分离并合成等效的虚拟阵列,从而能够获得更大的阵列孔径,提升DOA估计算法的角度分辨率和估计精度。
除了硬件性能上的改进,通过超分辨DOA估计的信号处理方法提升角度分辨率和精度也是毫米波雷达一项重要的研究课题。目前,DOA估计方法大致分为3类,包括非参数模型谱估计类算法、传统超分辨估计类算法、网格化超分辨估计类算法等。基于量测数据的非参数模型谱估计类算法[4,5],典型如CBF,Capon以及IAA,其优势在于简单易实现,但受限于阵列孔径或信噪比条件,在测角分辨率和精度上存在一定限制。基于子空间分解或拟合的传统超分辨估计类算法[6],典型如MUSIC,ML以及WSF,虽能够突破阵列瑞利限的限制,实现DOA超分辨精确估计,但本质上属于参数化方法,算法性能严重依赖于预设的模型参数,对实际应用场景和外部信号环境的要求较高[7]。基于稀疏信号表示和压缩感知理论的网格化超分辨DOA估计算法[8],典型如OMP-DOA,L1-SVD,RVM-DOA等,该类算法在离散角度域稀疏建模,对阵列孔径的依赖程度低,能够在少快拍(甚至是单快拍)、低信噪比、信源相关/相干等非理性外部环境下实现DOA的精确估计[9],但存在理想化网格假设所导致的固有DOA估计字典失配问题,虽然有学者后续又提出了如增加网格划分密度、网格不均匀划分、字典自校正等技术来进一步修正模型误差[10],改善该误差所带来的影响,但计算不稳定性的增加以及与精确稀疏重构条件之间的冲突进一步限制了算法性能的提升。为解决网格失配问题,近年来,基于原子范数理论和范德蒙德定理的无网格超分辨DOA估计算法受到了众多学者的广泛关注。由Chandrasekaran等人[11]提出的原子范数理论指出:原子范数利用原子集合凸包的连续特性来计算范数,能够在对信号施加稀疏约束的同时保证其参数空间的连续性[12],这相当于直接在连续域上进行稀疏建模,从而规避了网格离散化表示的过程。Tang等人[13]最先将原子范数理论引入无噪条件下的线谱估计问题中。Bhaskar等人[14]进一步对有噪情况下的复正弦叠加信号的频率和振幅估计问题进行了讨论,并提出原子范数软阈值(Atomic Norm Soft Thresholding,AST)算法。Yang等人[15,16]将线谱估计问题进一步扩展至DOA估计领域,并对等距均匀及稀疏阵列、完整及压缩数据场景下的基于原子范数最小化的DOA估计问题进行了研究。无网格超分辨DOA估计算法有着完备的理论支撑和成熟的数学工具,其本质在于以优化的方式重构阵列的协方差矩阵,然后利用该矩阵的范德蒙德分解实现目标的DOA估计,该类算法能够取得相较于前述网格化超分辨DOA估计算法更优的DOA估计性能,较符合车载毫米波雷达对于目标测向的高应用需求。
车载场景下时常面临上述非理想的信号环境,如当目标高速运动时,距离徙动造成相干累积时间减少,无法获得大量的独立同分布快拍数据;当雷达本身发射功率有限、毫米波大气传播衰减较大且目标的散射截面积较小时,接收信号的信噪比较低;当探测场景中存在来自地面或其余物体反射的多径,或包含来自同距同速紧邻目标的信号时,接收信号内将包含相关(相干)信号等。除非理想的外部信号环境外,毫米波雷达的待检测目标多为车辆、骑行者、行人等运动目标。为此,本文针对车载毫米波雷达应用所面临的实际问题,如少快拍、低信噪比、信源相干以及目标运动等情况,将研究重点放在对受限孔径条件下雷达角度分辨率和测角精度的提升上,提出了一种基于距离多普勒域原子范数最小化(Range-Doppler Atom Norm Minimize,RD-ANM)的毫米波雷达动目标超分辨DOA估计方法。该方法主要包括如下步骤:首先,构建基于动目标雷达回波的距离多普勒域阵列接收信号;其次,设计动目标多普勒耦合相位补偿矢量,用以削弱目标运动对DOA估计的影响;最后,提出了基于原子范数框架的多目标超分辨DOA估计方法。相较于车载毫米波雷达现使用的DOA估计算法,本文算法能够在基于低信噪比条件和单快拍处理前提下获得较高的测角分辨率和估计精度,以及拥有不牺牲阵列孔径对相干信号进行处理的稳健性能。理论分析、数值仿真以及实测实验验证了本文算法的有效性。
2 TDM-MIMO毫米波雷达动目标回波模型
考虑如图1所示的车载TDM-MIMO毫米波雷达探测场景[17],发射阵列是一个阵元数为MTX、阵元间距为dT的均匀线阵,接收阵列是一个阵元数为MRX、阵元间距为dR的均匀线阵,通常情况下,dR=λ/2,dT=MRXdR。在TDM-MIMO体制下,各个发射天线通过分时交替循环工作的方式发射LFMCW信号,接收阵列接收相应的回波信号,并进行模数转换、去斜以及合并处理,得到最终的等效虚拟单输入多输出(Single Input Multiple Output,SIMO)阵列的接收差频基带数字信号。假设空域包含K个远场目标,方位角分别为θ1,θ2,...,θK,以雷达开始工作时,第1个发射阵元所对应的第1个接收阵元作为参考阵元,暂时考虑目标低匀速运动,即距离徙动未超过一个距离单元的情况,则一个相干处理周期(Coherent Processing Interval,CPI)内,阵列接收到的差频基带数字信号模型[18]可以表示为

图1 车载TDM-MIMO毫米波雷达探测场景示意图Fig.1 Schematic diagram of vehicle borne TDM-MIMO MMW radar detection scene
其中,mt=1,2,...,MTX,mr=1,2,...,MRX,l=1,2,...,L为1个CPI内第l个LFMCW信号,L为每个CPI所包含的LFMCW信号数,fs为ADC采样率,n=1,2,...,N为快时间变量,N为单个LFMCW信号的ADC采样点数;k=1,2,...,K为目标索引,αk,ϕk,Rk,vk分别为目标的差频基带信号振幅、固定相位、初始距离以及运动速度,分别为目标的距离和多普勒频率;fc为发射载频,c为光速,λ=fc/c为发射波长;u=B/Tup为调频斜率,B为调频带宽,Tup为调频时间,Tc为斜坡重复周期,Tint=MTXTc为特定发射天线的发射时间间隔;wmt,mr(n,l)为均值为0、方差为σ2的加性高斯白噪声。
为便于后续信号分析和处理,将式(1)转化为
3 基于RD-ANM的毫米波雷达动目标超分辨DOA估计方法
由式(2)中的x(n,l),n=1,2,...,N,l=1,2,...,L构成了毫米波雷达的原始回波数据(Raw Data)块。如图2所示,对原始回波数据块中各接收通道对应的回波数据平面进行距离向和多普勒向的2DDFT[19](Two-Dimensional Discrete Fourier Transform)处理,得到距离-多普勒谱(Range-Doppler Map,RDM)矩阵块

图2 距离向和多普勒向的2D-DFT处理示意图Fig.2 Schematic diagram of range dimension DFT and Doppler dimension DFT
其中,q=1,2,...,N,p=1,2,...,L,D(q,p)表示第(q,p)点的2D-DFT变换结果。
对距离-多普勒谱矩阵块D(q,p),q=1,2,...,N,p=1,2,...,L进行阵列天线维模值叠加(非相干累积),两维单元平均恒虚警(Cell Averaging-Constant False Alarm Rate,CA-CFAR)检测以及峰值分组(Peak Grouping)处理,得到目标检测平面,此时与第k个目标相对应的平面内距离单元和多普勒单元将呈现峰值。提取峰值距离-多普勒单元坐标(qpeak,ppeak)后,即可对峰值距离-多普勒单元内所包含目标的距离及运动速度进行解算
在对目标的距离及速度信息进行解算的同时,回到距离-多普勒谱矩阵块,提取各接收通道的距离多普勒谱在(qpeak,ppeak)处的复数数据D(qpeak,ppeak),构建基于动目标雷达回波的RD域的等效虚拟SIMO阵列的接收单快拍数据
其中,z ∈Ω={1,2,...,Z}⊆{1,2,...,K}表示分布在D(qpeak,ppeak)这一距离-多普勒单元内的目标。为便于后续信号处理及分析,将其转换为
从式(7)可以看出,从RD域上提取出的复数数据仍然包含阵元间的相位差信息,可作为阵列的接收快拍数据,用于后续的DOA估计。基于RD域进行目标DOA估计的优势在于:首先,不同距离和速度的目标会在角度维处理前得到充分分离,使得某一距离多普勒单元上需要进行DOA估计的信源个数进一步降低;其次,该框架下获得的DOA估计结果能够与目标的距离及速度信息相互关联;然后,该框架下能够对动目标的距离/角度单元走动以及能量散焦进行预补偿处理,以削弱对后续DOA估计结果造成影响[20];最后,该框架下能够利用相参和非相参累积增益进一步提升目标检测的性能,还能够改善角度维的处理信噪比,有利于后续的DOA估计[21]。
从式(7)也可以看出,在TDM-MIMO体制下,由于发射天线的切换机制,来自不同发射天线的LFMCW信号间会存在一个时间差,运动目标的多普勒频率和该时间差所引起的相位变化会耦合到虚拟SIMO阵列目标导向矢量上,如若不在DOA估计前削弱该耦合相位的影响,则会导致最终的DOA估计产生错误。因此需要设计相应的耦合相位补偿矢量对动目标的耦合多普勒相位进行补偿,由于已经解算出了相应的距离-多普勒单元上的目标速度,可根据该速度解算值构造相应的相位补偿矢量对耦合在虚拟SIMO阵列目标导向矢量上的运动目标多普勒相位进行补偿
其中,·为点乘运算符,cz >0和ϕz ∈[0,2π)分别为sz的振幅和相位,a(θz)为第z个目标的虚拟SIMO阵列导向矢量。
获得RD域的阵列接收信号,并对信号中所包含的动目标多普勒耦合相位进行补偿后,即可基于原子范数相关理论,对目标DOA实现超分辨估计。对式(10)进行频率预处理,将DOA估计参数θ的取值范围由连续角度域映射至归一化连续频率域
其中,yvir即为最终所需的RD域上的阵列接收单快拍信号,fz=dR/λ(sin(θz)+1)∈[0,1),s为目标信号矢量,A(f)=[a(f1),a(f2),...,a(fZ)],a(fz)为经过归一化频率预处理后的第z个目标的虚拟SIMO阵列导向矢量
根据式(12)所述信号形式,定义原子a(f,ϕ)和原子集合为
从式(12)和式(14)可以看出,RD域上的阵列接收单快拍数据可由原子集合中原子的非负线性组合来表示,这与稀疏表示中接收信号可由冗余字典中原子的非负线性组合来表示类似,但不同于冗余字典原子参数的离散化取值,原子集合中原子参数f是在连续域上连续取值的,此时DOA的估计过程可以看成是从包含无限不间断原子的冗余字典中选取信号最稀疏表征的过程,这相当于直接在连续域上进行稀疏建模,规避了网格离散化表示的步骤,且算法性能不再受冗余字典原子间任意增加的相关性的影响。
由式(12)基于RD域原子范数最小化的去噪问题模型[16]可以表示为
其中,||·||A,1为l1原子范数
将式(15)转化为等价半正定规划(Semidefinite Program,SDP)形式[16]进行求解
其中,||yvir-x||为数据拟合项,γ为非负正则系数[14],用于平衡yvir的保真度以及构成x的原子系数矢量的稀疏度,x,u为待求解优化变量,u1为u中的第1个元素,t是自由变量,是避免出现平凡解的正则项。
通过求解式(17)所示的SDP优化问题可获得Toeplitz矩阵T(u),T(u)可看成是以优化方式重构出的低秩、半正定阵列协方差矩阵,其存在如下形式的范德蒙德分解[22]
其中,r=rank(T(u))
4 实验与分析
4.1 实验场景说明
本文实验场景设置如图3所示,在该实验场景中,我们考虑毫米波雷达静止,多个同初始距离目标以相同速度但不同角度相对雷达在同一平面内做匀速直线运动的情况,例如在图3中,平面内黑色点迹为TDM-MIMO阵列所处的位置,点目标(以绿色为例)相对雷达保持一定速度和角度做匀速直线运动,十字符号为该点目标的初始位置,当设定的运动方向为远离雷达的方向时,目标的运动轨迹将呈现为以十字符号为起点,偏离y轴设定角度的直线。后经实验证实该实验场景下多目标间信号是相干的,因此此时应用RD域-MUSIC算法已无法对目标来向进行正确的估计,而采用RD域-前后向空间平滑(Forward and Backward Spatial Smoothing,FBSS) MUSIC算法对目标信号进行解相干处理后才能够提取正确的目标DOA值,如图4所示。
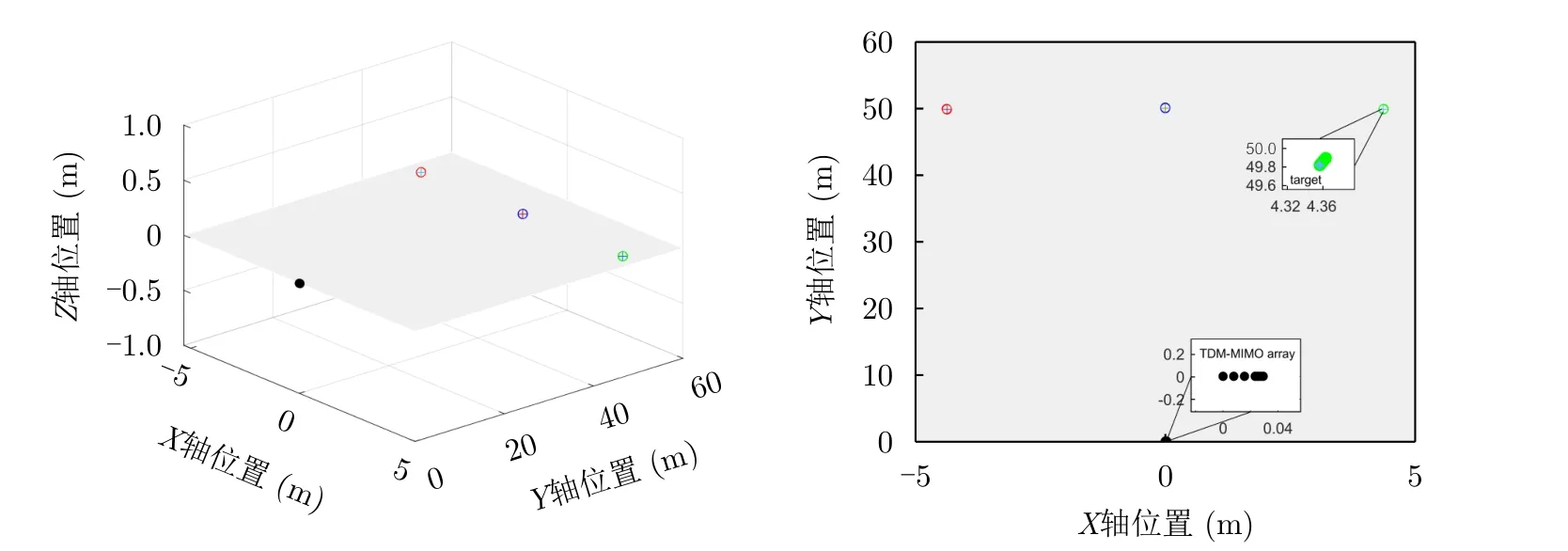
图3 目标与阵列相对位置示意图Fig.3 Schematic diagram of relative position between target and array
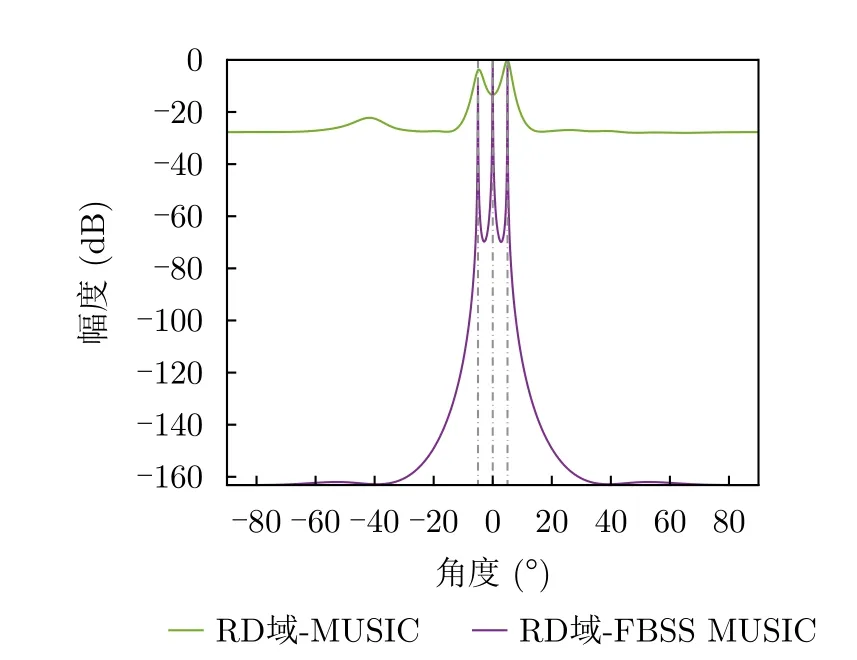
图4 RD域-MUSIC及RD域-FBSS MUSIC对相干信源的处理Fig.4 RD-MUSIC’s and RD-FBSS MUSIC’s processing of coherent sources
实验的仿真参数设置如表1所示。为验证本文算法在单快拍、低信噪比以及信源相干场景下的测角分辨率及精度,本文依次选取RD域-FFT (单快拍)、RD域-FBSS MUSIC (多快拍)、RD域-IAA(单快拍)以及本文算法(单快拍)进行对比,同时,本文选取均方根误差(Root Mean Square Error,RMSE)作为统计误差分析指标,其计算表达式为

表1 实验仿真参数Tab.1 The simulation parameters
4.2 计算复杂度对比分析
RD域-FFT的计算复杂度为O(MlogM),RD域-FBSS MUSIC的计算复杂度为(2PB(M -P+1)+P2B+P3+PKξ),RD域-IAA的计算复杂度为O(2M2K+MK+M3),本文算法计算复杂度为O(M3.5log(1/ζ)+M2+M3+MKξ),其中,N为LFMCW信号的ADC采样点数,L为每个CPI所包含的LFMCW信号数,M为阵元数,P为平滑子阵阵元数,B为快拍数,K为信源数,ξ为搜索次数,ζ为收敛精度。由图5可以看出,本文算法的计算复杂度较大,即以牺牲算力为代价来谋取较好的算法性能。

图5 计算复杂度Fig.5 Computational complexity
4.3 耦合多普勒相位对DOA估计的影响
设定目标数K=3,3个目标相对于车载毫米波雷达的初始距离及运动速度均设置为R=50 m,v=10 m/s,波达方位角分别设置为θ1=-40◦,θ2=-15◦,θ3=38◦。雷达原始回波信噪比根据基本雷达方程设置为22.5735 dB。TDM-MIMO阵列中接收阵列接收到动目标的雷达回波信号后,将进行模数转换、去斜以及合并处理,从而得到等效虚拟SIMO阵列的雷达原始回波数据块。对该原始回波数据块中各接收通道对应的回波数据平面进行距离向和多普勒向相参累积,可得到RD谱矩阵块,该RD谱矩阵块包含了后续信号处理所需的RD域数据。对雷达原始雷达回波数据块进行距离多普勒向二维相参累积后阵列单通道累积结果如图6(a)所示,基于RD谱矩阵块进行阵列天线维非相参累积、两维CA-CFAR检测(距离向CA-CFAR检测阈值如图6(c)所示,多普勒向CA-CFAR检测阈值如图6(d)所示)和峰值分组处理后,即可获得目标检测平面(图6(b)),由图6(b)可以看出,所设置的3个同距同速的动目标聚焦于检测平面内的同一距离多普勒单元处,获取该峰值距离-多普勒单元坐标,即可由式(5)、式(6)解算出包含在该峰值距离-多普勒单元内目标的距离及速度,由图6(b)获得的解算结果如表2所示,获得的3个同距同速目标的距离和速度解算值分别为50 m和9.8925 m/s,后续可将目标距离速度与来向三者间关联起来,以构成目标的三维参数信息。

表2 目标参数Tab.2 Target parameter
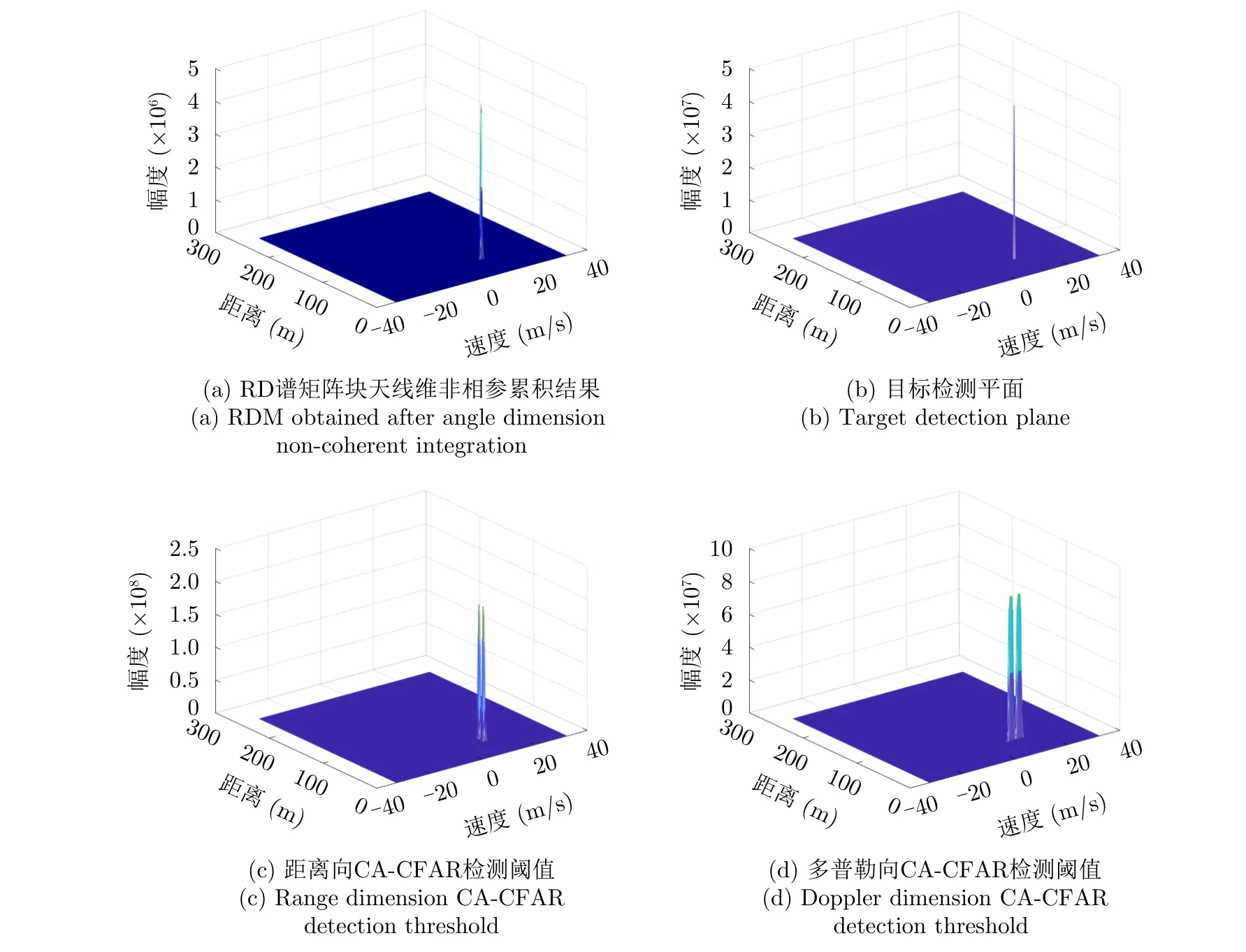
图6 目标检测Fig.6 Target detection
现在回到RD谱矩阵块,提取虚拟SIMO阵列各接收通道在峰值距离-多普勒单元处的复数数据,构造阵列接收单次快拍数据,以及提取RD谱矩阵块中峰值距离多普勒单元所在RA (Range-Angle)平面内复数数据,构造阵列接收的多次快拍数据(多快拍数据仅用于RD域-FBSS MUSIC算法的处理),分别采用RD域-FFT,RD域-IAA,RD域-FBSS MUSIC以及本文算法对目标进行一维DOA估计,DOA估计结果如图7所示。从图7所呈现的结果可以看出,若未在DOA估计前对动目标的多普勒耦合相位进行如式(9)、式(10)所示的预补偿处理,得到的DOA估计结果与目标真实波达方位角之间将存在较大的偏差,而经过了动目标多普勒耦合相位预补偿处理后DOA估计结果,能够正确地反映目标的真实来向,从而验证了在RD域进行DOA估计前对阵列接收中所包含的动目标多普勒耦合相位进行补偿的必要性。
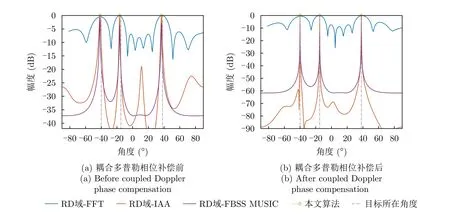
图7 耦合多普勒相位对RD域-DOA估计的影响Fig.7 Effect of coupled Doppler phase on RD-DOA estimation
4.4 不同角度间隔下DOA估计性能分析
大角度间隔下的DOA估计实验,基本参数设置同4.3节,3个目标波达方位角分别设置为θ1=-11.9◦,θ2=1.2◦,θ3=8.7◦;θ1=-5◦,θ2=0◦,θ3=5◦。DOA估计结果如图8所示。从图8可以看出,RD域-FFT由于受制于阵列孔径,算法的角度分辨率和估计精度均不高,无法分辨较近间隔的目标来向且DOA估计结果与目标真实来向间存在一定的偏差;RD域-FBSS MUSIC,RD域-IAA能够处理相干信源,且能够呈现较尖锐的谱峰,DOA估计结果较精确;本文算法性能与两者近似,同样拥有较高的测角分辨率和精度。4类算法的信噪比(Signal to Noise Ratio,SNR)-均方根误差(RMSE)如图9所示,从图9可以更为清晰地看出,RD域-FFT始终存在无法消除的均方根误差,RD域-FBSS MUSIC,RD域-IAA和本文算法3类算法性能近似,但本文算法的均方根误差在低信噪比条件下更低一些(图9(a),典型如–10 dB条件下,RD域-FFT,RD域-IAA和RD域-FBSS MUSIC的RMSE分别为9.5653°,3.1078°,11.4527°,本文算法的RMSE为0.2308°),进一步降低角度间隔,这种优势将更为明显(图9(b),典型如在–10 dB条件下,RD域-FFT,RD域-IAA和RD域-FBSS MUSIC的RMSE分别为8.4476°,20.4559°,27.8961°,本文算法的RMSE为0.5877°)。另外,为进一步测试本文算法在一定角度间隔下的信噪比极限,将原始回波信噪比降至–15 dB,重复实验结果如图10所示,蒙特卡罗实验次数设置为300,从图10可以看出,本文算法能够清晰分辨不同目标来向时的信噪比下界是随着目标角度间隔的减小而增加的,即目标来向越小,能清晰分辨来向所需的雷达原始回波数据的信噪比则越高。
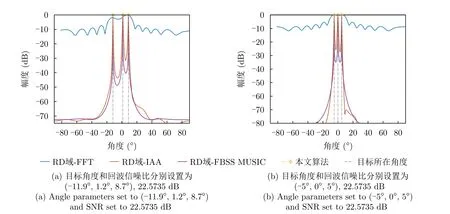
图8 大角度间隔下的RD域-DOA估计结果Fig.8 RD-DOA estimation results at large angle intervals
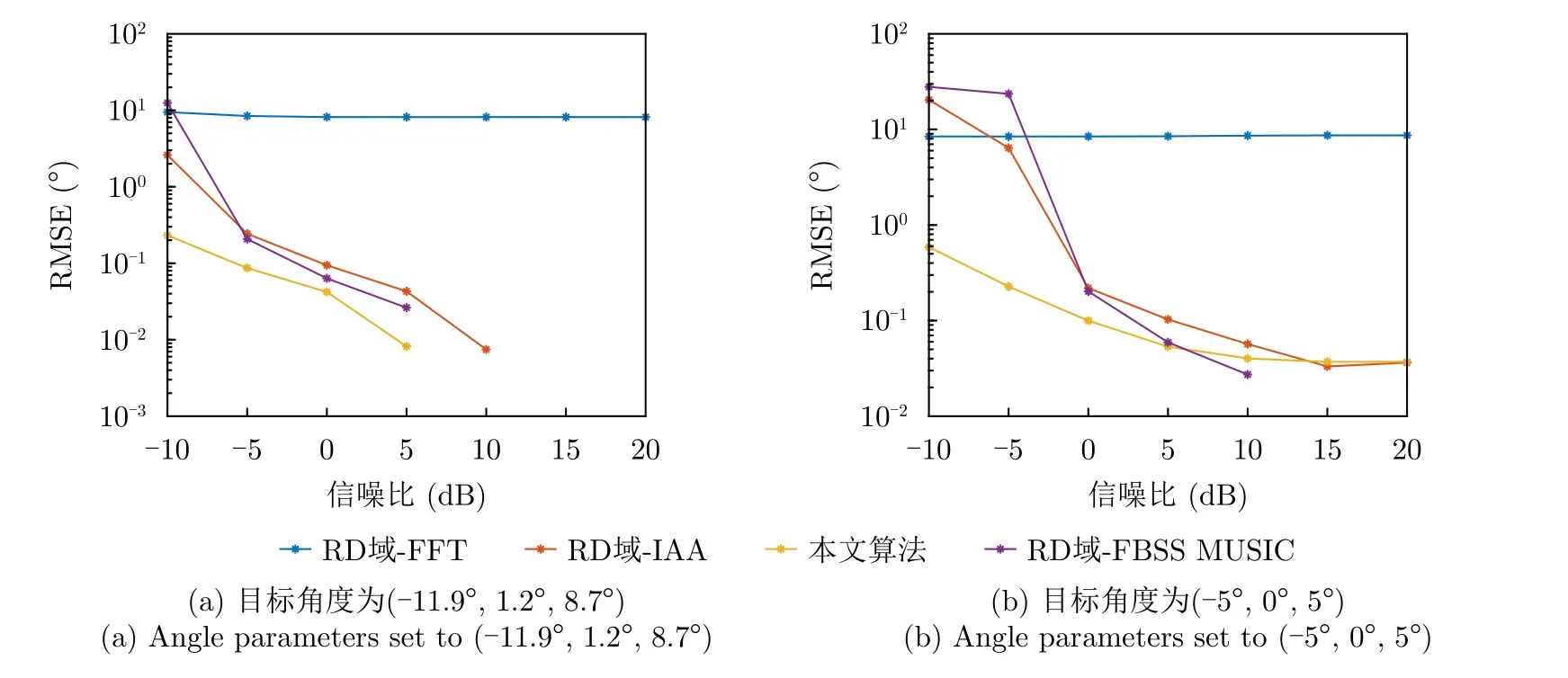
图9 大角度间隔下的信噪比-均方根误差图Fig.9 SNR-RMSE diagram at large angle intervals
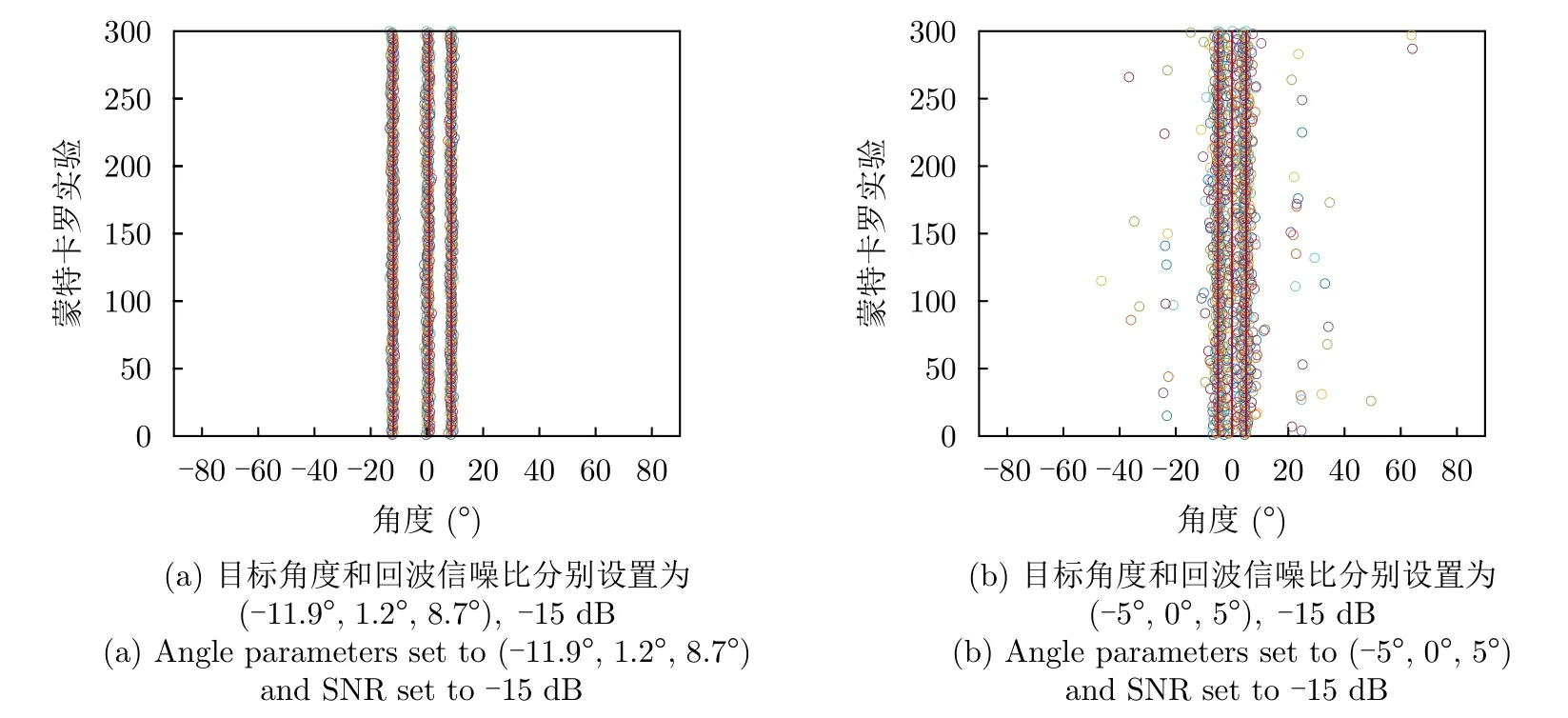
图10 大角度间隔下的蒙特卡罗独立重复实验Fig.10 Monte Carlo independent repetition experiment at large angle intervals
小角度间隔下的DOA估计实验,设定目标数K=2,两个目标相对于车载毫米波雷达的初始距离及运动速度均设置为R=50 m,v=10 m/s,波达方位角分别设置为θ1=-2◦,θ2=2◦;θ1=-1◦,θ2=1◦。如前文所述,越小角度间隔条件下能够清晰分辨目标来向的雷达回波信噪比越高,因此将雷达原始回波信噪比依据基本雷达方程设置为22.5735 dB,其余参数设置同4.3节。重复实验结果如图11所示,蒙特卡罗实验次数设置为300。
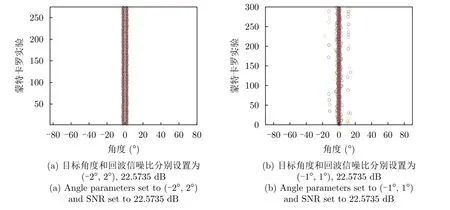
图11 小角度间隔下的蒙特卡罗独立重复实验Fig.11 Monte Carlo independent repetition experiment at small angle intervals
从图11可以看出,在目标小角度间隔(<5◦)且较高信噪比条件下,本文算法能够突破阵列孔径的限制,在目标参数空间间隔远低于1/⎿(DOF)/4」分辨率限制条件下[16,24],仍能以较高的概率检索出相应的目标角度参数。但需要指出的是,事实上,基于上述距离多普勒域的处理框架,在过小角度间隔条件下,RD域FBSS-MUSIC和RD域-IAA算法的性能会更好,本文算法若需达到相当的性能,需进一步增加(虚拟)阵列孔径。
4.5 相干信源分辨性能分析
考虑到车载毫米波雷达实际应用中可能接收到大量的相关/相干信号,故需要进一步验证本文算法对于相关/相干信源的分辨能力。实际上,对于相关/相干信源的情况,此时由阵列协方差矩阵构建的信号子空间的维数将降为1,信号子空间与噪声子空间相互渗透,两者间的强正交性被破坏,使用RD域-MUSIC算法对由RD谱矩阵峰值距离多普勒单元所在RA平面内的复数数据构成的阵列多快拍数据进行DOA估计时,算法性能较差,如图12(a)、图12(b)中绿色曲线所示,此时RD域MUSIC已无法对目标来向进行正确的估计。因此采用前后向空间平滑技术对经典MUSIC算法进行改进,平滑子阵的阵元数设置为虚拟SIMO阵列阵元数的一半。由于前后向空间平滑技术牺牲了阵列孔径对信号进行去相关(解相干),因此RD域FBSS-MUSIC算法可估计信源数也进一步降低,理论上可估计信源数降为2M/3,但经实验测试最多仅能估计5个相干信源。而本文算法基于原子范数理论,本质上仍是沿用压缩感知/稀疏表示框架对稀疏信号进行重构的过程,因此只要当入射信号的目标空间划分使其满足了稀疏特性时,即可无需任何预处理对目标信号解相干(这与网格化超分辨DOA估计方法类似),因此本文算法能够在不牺牲阵列孔径的基础之上对相干信号进行处理,可估计信源数达11个(图12(b)),但待估计信源数较多时,DOA估计结果会存在一定偏差,经实验测试,能够实现完全精确估计时的信源数为7个。
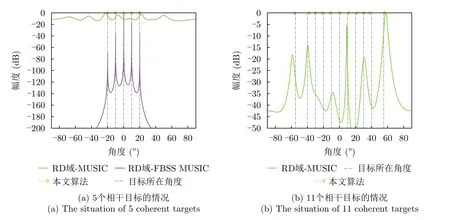
图12 可分辨相干目标数Fig.12 Number of resolvable coherent targets
4.6 实测实验及分析
本节基于车载毫米波雷达的实测数据对本文算法的有效性进行验证,由于试验条件有限,本次实验采用内场静止目标作为DOA估计对象。在实测场景中,TDM-MIMO阵列与目标间相对位置如图13所示。雷达系统主要由德州仪器(Texas Instruments,TI)公司的AWR2243 BOOST评估板卡(中心频率、调频时间及调频斜率分别设置为77 GHz,25.6 µs,30 MHz/µs)和DCA1000 EVM数据采集卡构成,TDM-MIMO阵列常规阵列合成所得到的角度分辨率为∆θres=λ/MdRcosθ ≈9◦。阵列与目标间的轴向距离(阵列与目标的y轴坐标间的相对距离)均设置为4.296 m,两组实测数据中两目标的径向距离(目标x轴坐标与y轴间的相对距离)分别设置为(–0.3 m,0.05 m),(0.35 m,0.5 m),由轴向和径向距离这两个距离参数可推演出目标相对阵列的角度参数,经演算,两组实测数据中目标角度参数分别为(–3.9946°,0.6668°),(0°,6.6386°)。现通过本文算法对两组实测数据中所包含目标的来向进行估计,获得的DOA估计结果如图14、表3所示,由两组实测数据获得的目标DOA估计值分别为(–4.1°,0.3°),(0.7°,6°),可以看到,基于实测数据分布于同一距离多普勒单元内的目标(存在相关性)DOA估计值和推演值间存在一定的偏差,但DOA估计的平均误差均保持在1°以内,实现了超分辨估计,从而验证了本文算法的有效性。

表3 实测DOA估计结果Tab.3 DOA estimation results based on practical data

图13 实测场景Fig.13 Practical scene
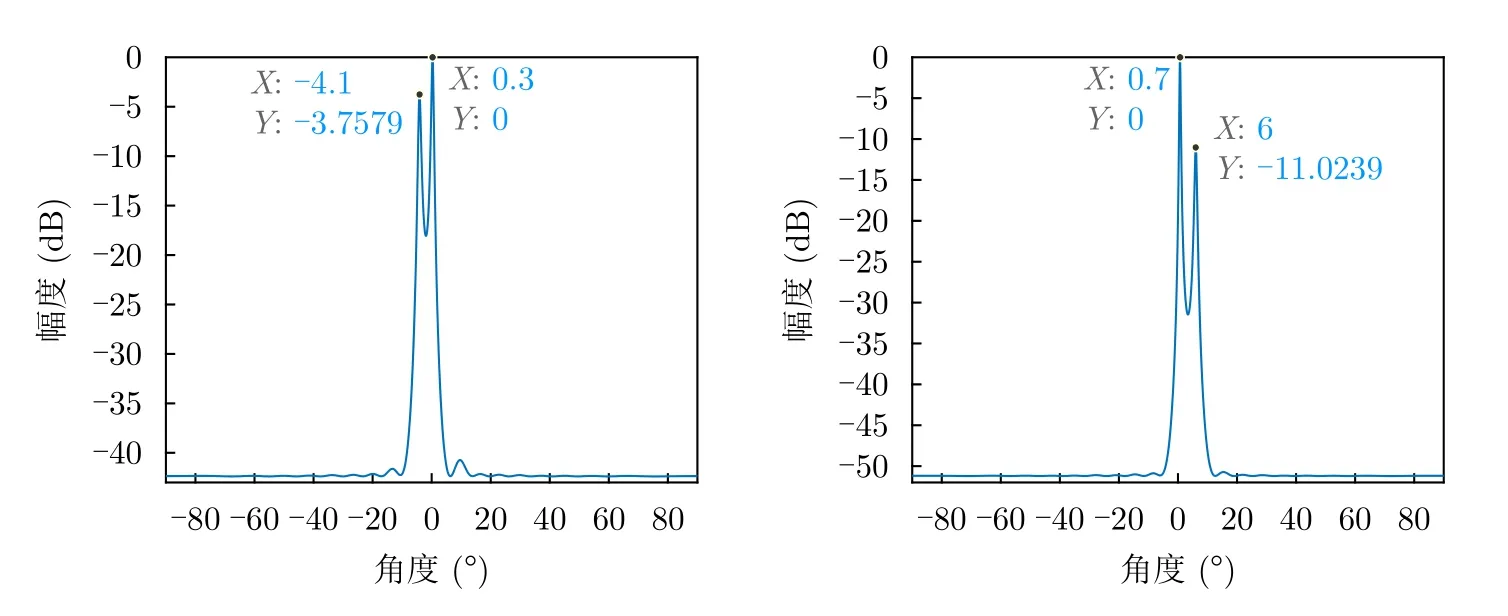
图14 实测1、实测2 DOA估计示意图Fig.14 Schematic diagrame of DOA estimation for test 1 and 2
5 结语
针对车载TDM-MIMO毫米波雷达动目标方位角估计问题,且考虑车载场景中常见阵列孔径受限、低快拍、低信噪比及信源相干的情况,本文提出了一种基于RD-ANM的毫米波雷达动目标超分辨DOA估计方法,理论分析、数值仿真以及实测实验验证了本文算法能够在非理想的外部环境下保持稳健的算法性能,有效地实现动目标的超分辨DOA估计,从而为车载毫米波雷达实现高精度、高分辨目标测向提供一种可能的解决方案。另外,本文考虑的场景较理想,没有考虑如目标高速运动、非相对运动所产生的距离、角度单元走动因素的影响,也没有对算法计算复杂度如何进一步降低进行相关研究,以及实测部分由于实验条件限制未获取到相应的运动目标数据等,这将会是我们下一阶段所要进行的工作。
