高温散体对流换热数值模拟Matlab编程实现

庞润芳，郑坤灿

(1.内蒙古科技大学工程训练中心，内蒙古包头 014010；2.内蒙古科技大学能源与环境工程学院，内蒙古包头 014010)

0 引言

高温散体广泛存在于化工、环保、冶金、建材、矿业等许多工业过程，而且在航空航天、核反应堆等领域也有着广泛应用，因此高温散体的高效热回收和强化传热问题近年来一直是多孔介质对流换热研究的热点和难点。人们对高温散体对流换热已经进行了一定的实验和数值模拟研究：马淑杰等[1]建立了烧结矿冷却过程的多孔介质模型，探讨了烧结矿热物性参数分别采用经验值和实验值对数值模拟的影响；夏建芳等[2]应用VB.NET语言,基于CFD平台,开发了环式鼓风冷却机烧结矿冷却过程自动仿真软件；刘立钧[3]采用有限差分法对烧结矿竖冷窑内气-固换热过程进行了数值模拟研究；倪文杰[4]将富氧和喷吹焦炉煤气与烟气循环联合使用,形成综合烧结工艺,通过数值模拟研究烟气循环条件下富氧和焦炉煤气喷吹参数对烧结工艺和产品质量的影响;刘玮寅[5]等通过仿真模拟软件COMSOL Multiphysics 对烧结矿竖罐式冷却过程进行数值模拟研究；冯军胜[6]等利用Fluent 软件及其二次开发平台对烧结矿余热回收竖罐内气固传热过程进行了数值分析；果晶晶[7]等采用CFD 软件对烧结矿余热罐内的气固换热过程进行了数值模拟研究;冯军胜[8]等借助Fluent模拟计算平台,利用正交实验方法对烧结矿竖罐内气固传热过程进行了数值模拟与优化；吴礼忠[9]等基于Fluent 模拟软件,通过使用UDS 和UDF 分别对函数方程和源项进行定义与修改,采用多孔介质模型对烧结矿层冷却过程进行模拟。本文选择了Matlab 语言来实现对高温散体对流换热过程的数值模拟。

Matlab 最早是专门针对矩阵简化运算开发的，所以被称为矩阵实验室(Matrix Laboratory) 。该软件具有强大高效的多维数据处理能力，可以进行数值分析、矩阵计算、科学数据可视化和非线性动态系统的建模与仿真等，具有代码简洁、编程效率高等特点,因此比其他同类软件操作简单方便[10-11]。同时软件还具有巨量的库函数，而且也可以方便定义自己库函数。

高温散体对流换热模型的数值模拟的基本步骤包括物理数学模型的建立、空间和数学方程的离散差分、代数方程的求解、计算机编程和结果分析处理。

1 高温散体对流换热模型的建立

1.1 高温散体冷却过程物理模型

目前工业高温散体对流换热常见工艺有气固逆流和气固错流两大类，一般固体为缓慢移动，本文以后者作为研究对象。假设某高温散体，温度在300～1 500℃之间，在冷空气中缓慢移动冷却直到降到某一特定温度下，冷却空气从高温散体下部垂直吹入散体料层，从上部进入烟罩或排放。整个过程可以简化为如图1所示的物理模型。

图1 高温散体冷却过程物理模型

1.2 高温散体对流换热数学模型

针对图1 所示的高温散体冷却过程，在料层较宽的情况下忽略边壁效应、宽度维数、长度维数，再假设高温散体由大小不同的球形颗粒随机堆积而成且各向同性，忽略对环境热损失、气体导热和辐射传热，高温散体三维数学模型就可以简化为一维非稳态模型，如式(1)到式(6)所示。

1)连续性方程

2)能量方程

①气体能量方程

结合连续性方程可以简化为：

②固体能量方程

③动量方程

高温散体多采用Ergun公式计算，即：

式中：ΔP—高温散体内部压降，Pa；

H—对应压降的高温散体高度，m；

de—当量直径，m。

④状态方程

式中：N—气体摩尔数，mol；

R—气体常数，8.314J/(mol·K)；

M—气体摩尔质量，kg/mol。

式(5-24)也可以写为另一种形式：PM=ρRT。

3)定解条件

初始时刻(t=0)，料层入口处初始料温为Ts0，空气入口处(z=0)，空气入口速度ug0.，空气温度为环境温度Tg0。

2 一维非稳态的数值求解

数值求解就是将时空离散化，把数学微分方程组转换为时空节点上的代数方程，最后解出所有节点的代数方程组，得到相应的温度时空分布。

2.1 离散代数方程组

数学方程离散方法有很多，而目前传热过程主要采取有限容积法，内部节点用有限差分，边角节点用热平衡法。针对一维非稳态模型，为了保证差分方程的稳定，采用隐式差分格式。

1)连续方程离散

式中：n—时间节点编号；

k—空间节点编号。

2)气体能量方程离散

a)内部节点

b)入口边界点：k=0，Tn,k=Tg0，Tg0为环境空气温度。

c) 出口边界点：k=kmax，根据能量平衡，忽略热损失，方程为：

3)固体能量方程离散

①内部节点

②入口边界点：k=0，根据能量平衡，忽略热损失，方程为：

式中，k=0时，T0,k=Ts0，Ts0为入料温度。

③出口边界点：k=kmax，根据能量平衡，忽略热损失，方程为：

3 数值求解思路及Matlab编程实现

3.1 数值求解思路

数值求解主要包括前处理（网格划分）、代数方程求解和后处理（结果分析处理），总程序框图如图2所示。

图2 程序设计总框图

3.2 数值求解编程实现

1)网格和变量初始化

划分时间网格和空间网格，时间用t表示，空间高度用z表示，节点编号为1、2、3……设置空气、散体物性参数、运动参数和散体结构参数等，如：

2)求解各时刻各空间节点温度和速度

①求解初始时刻各空间节点温度和速度

由于定解条件只知道t=0时的固体温度和z=0处的气体温度，初始时刻z≠0处的气体温度未知，所以先要假设初始温度场和压力场，进而算出速度场，采用迭代求解值反复修改初始温度场和压力场，直至温度场和压力场稳定，此时即得到初始时刻的真实温度，在此基础上就可以计算以后各个时刻的温度场了。该求解过程具体如图3所示。

图3 初始时刻温度计算流程图

②其余时刻各空间节点温度的计算

初始时刻的温度、速度和压力真值求出后，根据状态方程、初始压力、初始温度求出初始第一节点的密度，再结合初始速度利用Ergun 方程求出下一个节点的压力，该压力再通过状态方程可以得到该节点的密度和速度，于是利用TDMA追赶法求出该时刻该节点的温度。就这样反复采用该方法就可以求出下一个空间节点，下下个节点直至所有空间节点的温度、压力、速度和温度。此处要注意的是物性均随温度而变化，在该节点温度未求出时物性是按上一时刻的温度来计算的，所以误差就会产生，尤其是时间间隔取得较大时更为明显。改变的方法是再加一层循环，即把现在计算出的温度再代回去重新计算，直到新旧温度间的差值小于指定精度为止。

部分代码如下：

4 结果分析处理

对结果的分析处理一般称为后处理，采用图形显示更为直观，最后可以输出不同位置处料温变化和空气温度变化如图4 和图5 所示，也可以输出烧结矿和空气的时空温度场如图6 和图7 所示，还可以结合实验数据输出对比验证结果如图8所示等。

图4 烧结矿不同高度温度沿环冷机周向方向上的变化

图5 烧结矿不同高度处风温变化规律

图6 环冷机内部烧结矿的温度场

图7 环冷机内部冷却空气的温度场

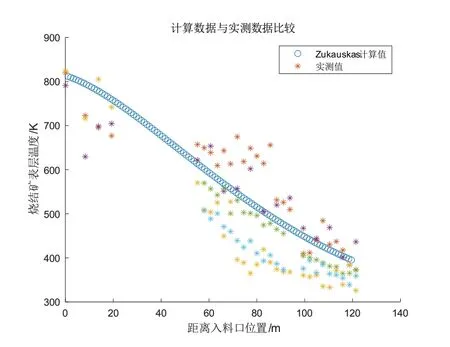
图8 计算数据与工业实测数据比较（湍流关联式）

固体温度变化代码（气体代码略）：

legend('Zukauskas 计算值','实测值')%,'Wakao and Kaguei','Kreith,Frank','Zukauskas','分形self',2)%,'nu7');,'nu6'

5 结论

论文利用Matlab 编写了高温散体对流换热通用计算程序，通过TDMA 追赶法求解了气流速度、气体温度和散体温度的时空离散解，实现了气固换热过程流动与传热的数值模拟。最后利用Matlab 强大的图形处理功能对数值模拟结果进行了可视化处理，获得了不同高度的风温和料温变化规律，绘制了全场的风温和料温分布图，展示了模拟计算结果和实验值之间的差别。