循环热力作用下压气储能洞室钢衬的疲劳耐久性

夏才初， 秦世康， 赵海鸥， 薛小代， 周瑜

（1. 同济大学 土木工程学院，上海 200092；2. 宁波大学 岩石力学研究所，浙江 宁波 315211；3. 大同启迪未来能源科技集团有限公司，山西大同 037000；4. 清华大学 电力系统及发电设备控制和仿真国家重点实验室，北京 100084）

实现碳达峰目标的首要措施就是减少化石能源的使用，增加风电、光伏电等绿色可再生能源的利用。风电、光伏电这些绿色可再生能源和传统化石能源相比虽然更加环保，但由于其间歇性和波动性的特点导致发电的稳定性和持续性相对不足。

为解决上述问题，就需要利用大规模储能技术，而压缩空气储能（Compressed air energy storage，CAES） 就是一种常用的大规模储能技术［1-2］。CAES技术以高压空气为媒介来实现电网中能量的存储和释放，通过对能量存储和释放的合理调控就可以将风电、光伏电这些间歇性能源转化为稳定、可控的优质能源。

其中，地下洞室作为高压空气的存储容器，在CAES电站的运行过程中具有重要作用，而其建设的关键问题就是地下洞室的密封性问题［3-4］。

目前，世界上仅有的2座商业化运行的CAES电站均以盐岩溶腔作为地下储气洞室，依靠盐岩自身的低渗透性实现气体的密封［5］。盐岩溶腔虽然是气体储存的理想场所，但是这种特殊的地质构造对地质条件要求苛刻，适用性较差。

为解决上述问题，北欧发展了一种更加灵活的利用内衬岩石洞室储存气体的技术，名为lined rock cavern（LRC），该技术中洞室结构主要由钢衬、混凝土衬砌和围岩组成。钢衬厚度一般为10～15mm，其主要作用是对高压气体进行密封但不承担气体压力，钢衬受力通过混凝土传递到围岩中［6］。

该技术使用之初主要是在天然气储存领域，二十世纪后在CAES领域也进行了相关尝试。KIM等［7-8］通过在一个钢衬密封的石灰岩矿洞进行高压储气试验证明了该方法的有效性。之后，Park等［9］将点估计方法与有限差分法相结合计算了高内压条件下钢衬密封层的稳定性，结果表明采用14mm极限强度为400MPa的钢衬可以承受15MPa空气内压产生的拉应力。

Perazzelli和Anagnostou［10］运用ABAQUS分析了围岩压力作用下钢衬的屈服现象，指出软岩地区（2GPa＜E＜5GPa）采用钢衬的储气洞室内压不能高于10MPa。周舒威等［11-12］推导了一种求解温度和压力共同作用下CAES内衬洞室力学响应的解析解，计算了典型循环周期内钢衬的应力应变情况。结果表明：由于存在温度应力，钢衬的环向拉应力在充气阶段反而是最小的，最大值反而出现在抽气阶段。

以上研究为CAES洞室钢衬的稳定性评估奠定了基础，但主要研究的是极限状态下或某个运营周期内钢衬的力学特性，没有考虑长期运营下CAES洞室钢衬在温度和应力反复作用下的疲劳特性。

针对以上问题，以大同云冈矿拟建的压气储能电站为例，构建压气储能洞室热力耦合计算模型，通过应力疲劳、应变疲劳、裂纹扩展疲劳三种疲劳分析方法对长期运行条件下钢衬密封层的耐久性进行研究，以期为CAES洞室钢衬的现场应用，提供设计依据和理论指导。

此外，在LRC技术中衬砌主要是起到传递荷载的作用，本身承担较小的应力，而且本文主要关注的是钢衬的疲劳耐久性，因此，以下分析中主要针对CAES运行工况下钢衬的力学性能及耐久性进行分析。

1 压气储能洞室热力耦合计算模型

1.1 控制方程

一个周期内CAES洞室的运营过程如图1所示，包括充气、储气、放气以及再次储气4个阶段。充气阶段，充入洞室的空气导致洞室压力升高，空气压缩产生热量使得洞室温度也会升高；而在放气阶段，高压空气从洞室中放出，洞室压力降低，空气膨胀吸收热量使得洞室温度降低。除了上述 2 种效应外，洞室空气与密封层、衬砌、围岩不断地进行热交换，该热交换倾向于减小洞室温度的变动幅度［13］。

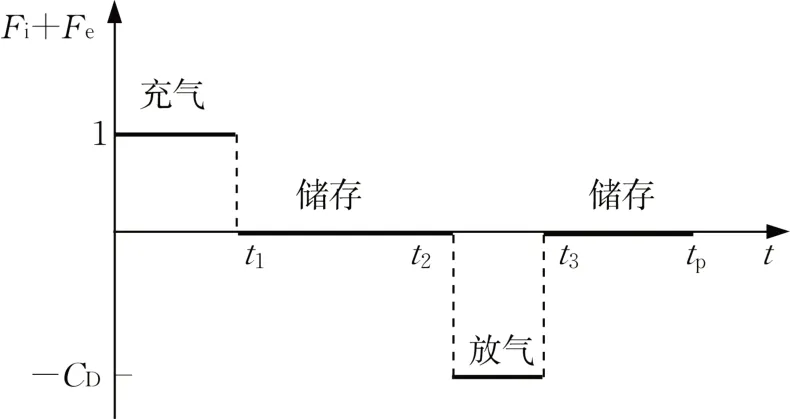
图1 CAES洞室的运行模式Fig.1 Operation mode of CAES caverns

压气储能洞室的热力耦合过程与常规热力耦合过程相比多了洞内空气的热力学变化过程。洞内空气的快速充放会造成洞内空气温度和压力的动态变化，而洞内空气的温度和压力是洞室结构温度场和应力、应变求解的边界条件。因此，CAES洞室的热力耦合计算过程和常规热力耦合过程相比要用两部分控制方程进行描述［14］：

（1）洞室的热力学部分，采用Kushnir R. 等提出的热力学控制方程［3］：

式中：V为洞室体积；ρ和ρ0分别为洞内任意时刻和初始时刻的空气密度（kg·m-3）；t为运营时间（s）；Fi，Fe为量纲为一的周期性函数（如图1所示，CD为放气速率与充气速率的比值）；ṁc为空气的充放气速率（kg·s-1）；cv0和cp0分别为空气的定容比热和定压比热（J/（kg· K））；T和Ti分别为洞室空气温度和注入空气温度（K）；R为气体常数（J/（kg· K））；T0为洞内各层介质的初始温度（K）；ZT0为空气压缩函数对时间求导后在温度T0处的取值；Q̇为洞内空气与密封结构的热交换速率（W）；hc为洞室空气与密封层的热交换系数（W·（m2· K）-1）；Ac为洞室表面积（m2）；T1（r0，t）为洞壁温度（K）；ρj、cpj、kj和Tj为第j层介质的密度、比定压热容、导热系数和温度，j=1， 2， 3分别代表钢衬、衬砌和围岩；rj-1和rj分别为第j层介质的内边界半径和外边界半径；Z为空气压缩系数。

（2）洞室结构受力采用经典的热弹性力学控制方程：

式中：σ为应力张量；Fv为体力矢量；σ0为初始应力张量；C为弹性张量；ε为应变张量；εinel为热膨胀引起的应变张量；α为热膨胀系数；I为单位张量。

1.2 计算模型

（1）工程背景

为加快城市转型，山西省大同市结合本市实际情况，拟利用云冈矿停用的1 030北大巷及980皮带巷作为CAES电站的储气空间，建设首期60MW、总规模100MW的CAES电站［15］。两条巷道平均埋深约300m，围岩由细砂岩和粉砂岩组成，围岩结构面整体发育较弱，围岩工程地质类别以Ⅱ～Ⅲ类为主，可利用的洞室储气总容积约90 000 m3。为保持巷道良好的受力性能，将原巷道进行扩挖改造，改造后的巷道形状为内径4.8m的圆形，洞内壁浇筑0.35m厚的钢筋混凝土衬砌，衬砌内壁铺设10mm厚的钢衬作为密封层，如图2所示。

图2 改造后巷道断面图Fig.2 Section view of roadway after transformation

（2）数值计算模型

根据改造后巷道断面的几何形状，通过有限元模拟软件COMSOL建立循环温度和内压作用下CAES内衬洞室的热力耦合计算模型。洞室以24 h为一个运营周期：充气8 h，储气4 h，放气4 h，再储气8 h。整个洞室结构的初始温度为28℃，注入空气温度为21.5 ℃，注入空气速率为175 kg·s-1，充气前洞室初始运营压力为4.5MPa，充气后洞室最大运营压力为10.0MPa。洞室按照平面应变问题进行考虑，且假设洞室传热是一维径向传热问题，模型范围取6倍洞径，边界条件如图3所示，具体计算参数如表1所示，对流换热系数为45 W·m-1·K-1。计算过程中首先通过COMSOL中的固体力学模块对洞室开挖后的应力状态进行计算，得到初始状态下围岩内的应力分布，继而在上述应力分布的基础上，通过控制方程（1）～（9）对压气储能洞室的运行过程进行计算，计算过程中监测P1处钢衬的温度、应力、应变等数据。

表1 CAES洞室结构的物理力学参数Tab.1 Physical and mechanical parameters of cavern structure

图3 数值计算模型及边界条件Fig.3 Numerical calculation model and boundary conditions

2 长期运营下钢衬的力学性能

在进行钢衬的疲劳耐性分析之前，首先要知道CAES系统运行过程中钢衬密封层应力、应变变化情况。对于钢材其受力情况受温度场影响较大，而相关研究表明硬岩洞室内压气储能温度场在50次循环之后达到稳定［3］，考虑到计算时间的问题，进行60个周期的计算。

2.1 钢衬和洞内空气的温度、压力

图4a、4b分别是60个运营周期内洞室温度和钢衬温度的变化情况，由于围岩吸热，前2个周期内洞室温度、钢衬温度略有下降，2个周期后由于围岩吸热量减小且注入空气温度高于洞室初始温度，所以洞室温度、钢衬温度逐渐升高，运营60个周期后，洞室温度、钢衬温度升高约3°C，但增幅逐渐减小。图4c是60个运营周期的洞内空气压力，由于钢衬密封层是不透气的密封层，洞内空气压力变化不大，基本在4.2MPa到10MPa之间变化。

图4 60个运营周期内钢衬和洞内空气的温度及压力Fig.4 Temperature and pressure of steel lining and cavity air for 60 operating cycles

2.2 钢衬的力学性能

图5a、b、c分别是60个运营周期的钢衬径向应力、环向应力以及纵向应力（本文中应力均取拉为正，压为负），钢衬径向应力与洞室压力相平衡，其变化规律正好与洞室压力相反。由于温度应力的作用，钢衬的环向应力逐渐减小，而纵向压应力逐渐增大，纵向拉应力逐渐减小。

图5 60个运营周期内钢衬的应力变化Fig.5 Stress variation of steel lining during 60 operating cycles

图5d是60个运营周期内钢衬Mises应力变化情况，随着运营周期的增加，充气阶段和抽气阶段Mises应力逐渐增大，其原因主要是钢衬径向应力几乎不变，而环向、纵向的温度压应力急剧增大（曲线向负向移动），使得充气阶段三个方向的应力差变大。最大Mises应力总体上呈先减小后逐渐增加的趋势，60个周期内从74.62MPa先减小到68.69MPa再增加到78.07MPa。最大Mises应力后期增大的趋势符合对数形式，进行拟合后得到拟合方程y=5.70×ln（t+17.73）+32.67，外推104个周期后最大Mises应力将增大到85.18MPa，仍小于钢衬的屈服强度355MPa。

图6分别是60个运营周期内钢衬径向应变和环向应变变化情况，可以看到由于温度应力的作用，钢衬的径向应变在前两个周期略微减小之后均随着运营周期的增加而增大，环向基本保持不变。和径向应变相比，环向应变较大，但基本维持在6.0×102με，小于钢衬的屈服应变0.17%。

图6 60个运营周期内钢衬应变的变化Fig. 6 Strain variation of steel lining during 60 operating cycles

3 钢衬的疲劳耐久性分析

CAES洞室的运营寿命一般在30年左右，在此期间钢衬会经历接近104量级的应力应变循环，因此，在进行钢衬密封层的结构设计过程中需要考虑循环热力作用下钢衬疲劳破坏问题。下面将通过应力疲劳分析、应变疲劳分析和裂纹扩展疲劳分析三种方法对CAES洞室钢衬密封层的耐久性进行研究。

3.1 应力疲劳分析

钢结构设计规范［16］中的疲劳计算采用容许应力幅法，应力按照弹性状态计算，对应力循环内应力幅保持常量的常幅疲劳，计算如下：

式中：Δσ=σmax-σmin，σmax是计算部位每次应力循环中的最大和最小应力（MPa）；[Δσ]是常幅疲劳的容许应力幅（MPa），计算如下：

式中：n为应力循环次数；C、β为参数。

本文中的钢衬构件可以按照规范中的“无连接处的主体金属”中的“钢板”进行选取，取偏保守的类别，C=861×1012，β= 4。按照式（11）进行计算，本案例中钢衬的容许应力幅为541.69MPa。根据长期运营条件下钢衬的应力计算结果，钢衬的径向应力、环向应力、纵向应力变化幅值分别为5.80MPa、53.52MPa、77.70MPa，均远小于许用应力幅值，因此，从应力疲劳分析来说钢衬满足疲劳要求。

3.2 应变疲劳分析

利用LRC技术进行天然气存储过程中同样面临着钢衬疲劳的问题，为此从应变角度提出了估算LRC钢衬疲劳寿命的计算公式［17］：

式中：Δε是应变变化幅值；σ'f是疲劳强度系数；ε'f是疲劳延性系数；b、c是材料参数。

该公式既适用于低周疲劳寿命的计算也适用于高周疲劳寿命的计算。同时为了方便应用，Manson在该公式基础上又提出了一种近似的估算公式，称为Manson 统一斜率公式［18］，即

式中：Δε是应变变化幅值；εf为拉断伸长率；σB是破坏强度，MPa；E是弹性模量，MPa；Nf是疲劳寿命，即破坏循环次数。

该公式可以基于单轴抗拉试验结果估算应变-疲劳寿命曲线。Johansson［19］对12mm厚的LRC钢衬（型号S355J2G3）进行单轴抗拉试验，得到了钢衬的疲劳参数εf=0.37，σB=527 MPa，并且其弹性模量为205 GPa。本文案例使用和LRC技术相同的钢材，应用式（13）估算钢衬的疲劳寿命。根据长期运营下钢衬应变变化情况，可知径向应变变化幅值为6.32×102με，疲劳寿命为4.14×109次，而环向应变变化幅值为3.83×102με，疲劳寿命为2.66×1011次，两者疲劳寿命均大于CAES洞室钢衬的运营要求。实际上，CAES洞室要求的疲劳寿命为104量级，代入式（13）可以得到相应的应变变化临界幅值为5.20×103με。因此，只要应变变化幅值小于该临界值，钢衬就不会发生疲劳破坏。

3.3 裂纹扩展疲劳分析

除了上述两种疲劳分析方法外，断裂力学的方法也经常被用来估算金属材料的疲劳寿命。按照断裂力学的观点，任何金属材料自身都存在初始裂纹缺陷，假设初始裂纹尺寸为ai，在交变应力作用下，裂纹会逐渐扩展，当它达到临界裂纹尺寸af时，就会发生失稳扩展而断裂。裂纹在交变应力作用下由ai到af这一扩展过程被称为疲劳裂纹的亚临界扩展，而这一扩展过程所需要的循环周期就是金属的疲劳寿命。

Paris公式［20］是描述金属裂纹扩展速率的经典公式：

对式（14）进行积分得到计算金属疲劳寿命的一般形式：

式中：a是裂纹尺寸（mm）；N是疲劳寿命；C是试验测定系数；ΔK是应力强度因子变化幅值（MPa）；n是材料参数。

根据英国金属结构裂纹验收评定方法指南（BS 7910：2013）推荐［21］，钢在空气中的疲劳裂纹扩展系数C=6.77×10-13、n=2.88（该参数适用于非侵蚀性环境下空气温度不超过100°C的情况，满足钢衬在CAES洞室运行环境的要求）。

由于张开型裂纹（I型）容易引起突然的断裂，所以，I型裂纹一般是最危险的。即使实际裂纹是复合型的，也往往把它当做张开型来处理，这样既简单又安全。因此，主要对钢衬的I型裂纹进行分析。由于存在埋藏裂纹和表面裂纹两种裂纹类型，并且这两种裂纹应力强度因子计算公式不一样，因此，下面分别对这两种裂纹影响下钢衬的疲劳寿命进行计算。

（1）考虑埋藏裂纹影响的CAES洞室钢衬疲劳寿命

Irwin公式是计算椭圆裂纹周界各点应力强度因子KI的经典公式［22］：

式中：σ为拉应力（MPa）；a是椭圆短轴（mm）；c是椭圆长轴（mm）；φ为椭圆周界点—圆心连接线与椭圆长轴的夹角（°）；Φ是第二类椭圆积分，其数值和椭圆轴比a/c有关，当a/c一定时，Φ是个常数，计算见式（17）。

由式（16）和（17）可知，椭圆裂纹短轴段KI有最大值：

由式（15）和（18）可知考虑埋藏裂纹影响的CAES洞室钢衬疲劳寿命为

（2）表面裂纹影响下CAES洞室钢衬疲劳寿命

除了埋藏裂纹外，CAES洞室的钢衬还必须考虑内表面裂纹引起的疲劳问题。实际情况中表面裂纹很少是直线型的，一般可视作半椭圆表面裂纹，考虑形状因子、自然边界和塑性区的影响，则内表面半椭圆裂纹的应力强度因子可由式（20）计算得到［23］。

其中：

式中：σθ为无裂纹时内表面处的环向应力（MPa）；σs是钢衬屈服应力（MPa）；p是洞室压力（MPa）；d是钢衬厚度（mm）。

由式（15）和（20）可得考虑表面裂纹影响的CAES洞室钢衬疲劳寿命为

式中：Δσθ为无裂纹时内表面处的环向应力的变化幅值（MPa）。

（3）CAES洞室钢衬的裂纹扩展疲劳分析

参照LRC钢衬的疲劳分析，根据钢衬的出厂质量控制指标，钢衬埋藏和表面裂纹的初始尺寸选取半径为3mm的圆形裂纹。而临界裂纹尺寸采用两种方法确定：一种是参照LRC钢衬直接选取4.6mm允许裂纹深度；另一种是根据钢衬的断裂韧度KIc=93 MPa·m1/2（参考Damjanac等的取值［24］）通过式（16）和（20）反算得到，钢衬的断裂韧度是钢衬的固有属性，此外，反算得到的裂纹临界尺寸不能大于钢衬厚度。

通过式（16）和（20）可以得到埋藏裂纹和表面裂纹的应力强度因子，通过式（19）和式（23）可以得到埋藏裂纹和表面裂纹的疲劳寿命，计算结果如表2所示。按照断裂韧度计算埋藏裂纹扩展的疲劳寿命时，埋藏裂纹需要扩展到2 240mm才能达到断裂韧度，这远大于钢衬厚度，因此在实际情况中不可能发生。真实情况是当埋藏裂纹短轴扩展到钢衬厚度的一半5mm时，钢衬就会被裂纹贯穿发生破坏，此时钢衬的真实疲劳寿命为2.85×106次。

表2 长期运营条件下CAES洞室钢衬的疲劳寿命计算结果Tab. 2 Fatigue life of CAES cavern steel lining under long-term operation conditions

从表2可以看出，表面裂纹的应力强度因子大于埋藏裂纹，疲劳寿命小于埋藏裂纹，这与断裂力学理论中表面裂纹较埋藏裂纹弹性约束减少、应力强度因子增大、疲劳寿命减小的结论是相符的［23］。此外，在表面裂纹计算出来的疲劳寿命中按照允许裂纹尺寸计算出来的疲劳寿命小于按照断裂韧度计算得到的疲劳寿命，因此，从安全性的角度考虑，钢衬的疲劳寿命可以用允许裂纹尺寸计算的表面裂纹寿命来表示。因此，钢衬疲劳寿命为1.25×106次大于CAES洞室要求的1×104次，说明长期运营条件下考虑表面裂纹扩展计算出的钢衬疲劳寿命也是满足疲劳要求的。

其他条件不变的情况下，通过式（19）和（23）可以反算得到CAES洞室运营期限（104次）内表面裂纹和埋藏裂纹对应的临界应力变化幅值分别为326MPa和370MPa，较容许应力幅541.69MPa小了近一半；同时，按照裂纹扩展疲劳法获得的钢衬疲劳寿命1.25×106次比按照应变疲劳法获得的疲劳寿命4.14×109次小3个数量级，这说明按照应力疲劳分析和应变疲劳分析两种方法过高估计了钢衬抗疲劳能力，容易造成偏危险的结果，钢衬疲劳分析中必须考虑裂纹扩展的影响，下面将对影响钢衬裂纹扩展疲劳寿命的影响因素进行进一步的分析。

3.4 钢衬疲劳寿命的参数敏感性分析

由式（19）和式（23）钢衬的疲劳寿命计算公式可知，决定钢衬疲劳寿命的因素主要有应力变化幅值、裂纹尺寸和钢衬厚度，而应力变化幅值主要由围岩弹性模量和洞室运营压力决定。

（1）围岩弹性模量和洞室运营压力对钢衬疲劳寿命的影响

图7是围岩弹性模量对钢衬疲劳寿命的影响，其他参数不变情况下，随着围岩弹性模量的增大，钢衬的疲劳寿命逐渐增大，当围岩弹性模量大于10GPa时，钢衬疲劳寿命的增幅大幅增加。当围岩弹性模量为5GPa时，表面裂纹和埋藏裂纹的疲劳寿命分别为0.52×105次和0.80×105次，此时钢衬疲劳寿命仍满足CAES洞室的运行要求，但已经非常接近CAES洞室的服务年限了。造成这种现象的原因在于，在围岩条件较差情况下，钢衬作为主要承载结构将发生更大的变形，相应的应力变化幅值也会更大。因此，压气储能洞室应选择在质量较好的围岩建造，围岩的弹性模量最好大于10GPa。

图7 围岩弹性模量对疲劳寿命的影响Fig. 7 Influence of surrounding rock elastic modulus on fatigue life

图8是洞室运营压力对钢衬疲劳寿命的影响，其他参数不变的情况下，随着洞室最大运营压力的增加，钢衬的疲劳寿命迅速减小，并逐渐趋于稳定。造成这种现象的原因在于，在初始空气压力不变的情况下，随着洞室最大运营压力的增加，一个周期内钢衬承担的载荷变化幅值逐渐增大。此外，由图8可知，在其他参数不变的情况下（围岩弹性模量为14GPa，洞室初始空气压力为4.5MPa），洞室最大运营压力从10MPa增大到15MPa时，钢衬的疲劳寿命减少了近70%，说明在此范围内钢衬的疲劳寿命比较敏感，因此，洞室的运营压力不宜过大，最好不大于10MPa。

图8 洞室运营压力对疲劳寿命的影响Fig. 8 Effect of cavern operating pressure on fatigue life

（2）裂纹尺寸和钢衬厚度对疲劳寿命的影响

钢衬的疲劳寿命取按允许裂纹计算的疲劳寿命，图9a为初始裂纹尺寸ai对钢衬疲劳寿命的影响，其他参数不变的情况下，随着初始裂纹尺寸ai的增大，钢衬的疲劳寿命迅速减小。ai为从1mm增大到4mm，钢衬疲劳寿命的数量级从107减小到了105，减小了2个数量级。因此，钢衬施工时需要严控钢材自身以及其焊接的质量，尽量减小钢衬的初始裂纹尺寸。

图9 裂纹尺寸对钢衬疲劳寿命的影响Fig. 9 Influence of crack size on steel lining fatigue life

图9b是裂纹短轴与长轴比对钢衬疲劳寿命的影响。可以看到，钢衬的疲劳寿命随着裂纹短轴与长轴比的减小而减小。当裂纹短轴与长轴比等于1（短轴与长轴相等，圆形裂纹），钢衬的疲劳寿命为1.25×106（表面裂纹）、2.43×106（埋藏裂纹），当裂纹短轴与长轴比等于0.1时，钢衬的疲劳寿命减小为3.56×105（表面裂纹）、6.90×105（埋藏裂纹）。这意味着裂纹形状越尖，应力越集中，应力强度因子越大，钢衬的疲劳寿命越小。

图10是钢衬厚度对钢衬疲劳寿命的影响。由于这里是按照允许裂纹计算的疲劳寿命，埋藏裂纹影响下钢衬疲劳寿命受允许裂纹尺寸控制，钢衬厚度没有影响。但是，钢衬厚度增大会增加表面裂纹时的疲劳寿命，增幅在厚度小于15mm时比较明显，而后逐渐减小，这说明钢衬厚度增大到一定程度后对疲劳寿命的作用就不明显了，因此，选择该厚度作为钢衬厚度是比较合适的。

4 结论

（1）钢衬疲劳寿命计算中必须考虑裂纹扩展的影响，应力疲劳法和应变疲劳法由于没有考虑裂纹扩展的影响，会使疲劳寿命计算结果偏大。裂纹扩展疲劳分析中按照允许裂纹尺寸计算表面裂纹扩展的疲劳寿命是偏安全的，可以用来代表钢衬的疲劳寿命，典型工况下（运营压力为4.5～10.0MPa，围岩弹性模量为14GPa）钢衬的疲劳寿命为1.25×106次，在CAES洞室的使用年限内不会发生疲劳破坏。

（2）钢衬裂纹扩展疲劳分析表明：钢衬疲劳寿命主要受围岩弹性模量、洞室运营压力和初始裂纹尺寸影响，钢衬疲劳寿命随着围岩弹性模量的增大而增大，随着洞室运营压力和初始裂纹尺寸的增大而减小。因此，为保证钢衬在使用年限内不发生疲劳破坏，可以对钢衬表面进行涂层处理，严格控制初始裂纹尺寸，此外，尽量在围岩质量较好的地方建造CAES洞室，且洞室运营压力不宜过大。

（3）钢衬厚度对钢衬的疲劳寿命也有一定的影响，钢衬的疲劳寿命随着钢衬厚度的增加而增加，但存在某一临界厚度，超过该厚度后钢衬的疲劳寿命就不会有明显变化，因此，工程上可以选择该厚度作为钢衬密封层的最佳厚度，计算得到的最佳厚度为15mm。

作者贡献声明：

夏才初：研究思路、理论指导及文章修改；

秦世康：数值计算模型及疲劳耐久性分析；

赵海鸥：依托工程地质资料的提供；

薛小代：热力学计算参数的提供；

周瑜：钢衬的力学性能分析。