基于差分进化算法的钢轨轮廓迭代旋转配准方法
2023-11-06沈伦旺马子骥刘宏立蒋志文
沈伦旺,马子骥,刘宏立,蒋志文
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
钢轨廓形检测在轨道质量检测中占有重要地位,通过将测量轮廓与标准轮廓进行对比,分析钢轨磨耗状态,为钢轨维护保养提供科学依据[1-2]。
轮廓配准是钢轨断面轮廓检测中的重要步骤,主要实现实测轮廓到标准轮廓坐标系的转换。只有钢轨轮廓的准确匹配,才能保证磨耗计算的精确性[3-5]。目前非接触式钢轨断面轮廓测量主要采用激光视像技术或激光位移技术实现,因此,基于钢轨断面二维点云数据的配准方法是当前主流技术之一。谭周文等[6]提出基于轨腰圆心拟合配准,其配准精度高,当采样的钢轨轮廓数据不理想,轨腰轨底有缺失时,则无法完成配准。文献[7-9]提出基于轨侧直线和轨颚点的直接配准,该方法配准速度快,且不受轨腰轨底数据的影响,但其配准精度相对不足。另外,刚体ICP配准法[10-12],要求测量轮廓与标准轮廓曲线覆盖范围基本一致,这点在实际应用中是很难满足的。
在实际检测采样中,由于列车原本就比较注重轨道表面的异物清除,因此轨头部分的采样极少受到干扰;而轨腰、轨底部分,受鱼尾板、道旁异物等的影响,采样轮廓往往与标准廓形相去甚远。因此,为了保持在噪声环境,甚至轮廓轨腰、轨底数据缺失等恶劣条件下的配准精度,需要重点提高配准方法的鲁棒性。本文提出一种基于差分进化算法的轮廓迭代旋转配准方法,该方法不以钢轨轮廓中的某个直接采样点为特征,而是从特征线段中重构特征点[13],从而保证在噪声干扰严重的情况下依然能够捕捉到钢轨断面轮廓的特征信息。以钢轨轨颚点为旋转中心,根据采样轮廓相对标准轮廓的位置确定采样轮廓的配准旋转的方向。借助差分进化算法寻找最优的旋转角度,根据旋转角度计算最优的旋转矩阵R以及根据轨颚点为中心计算出的平移矩阵T实现钢轨轮廓的精确配准[14-19]。实验结果表明,该方法具有很高的配准精度和鲁棒性。
1 轮廓形态分析
1.1 测量轮廓形态定义
以我国铁路线上最常用的60 kg/m钢轨为例,标准轮廓断面见图1(a)。它由轨头、轨腰、轨底组成。轨头区点A为轨颚点,由1∶20、1∶3直线相交而成。A′A为轨头侧面直线,点Z为轨侧直线A′A的中点。轨腰区BC为R=400 mm圆弧,CD为R=20 mm圆弧,两者切于点C;轨底区DE、EF分别为1∶3、1∶9直线,两者交于点E。

图1 钢轨数据介绍
轮轨接触示意见图1(b)。由图1(b)可知,主要接触磨损区域在轨顶至轨侧上部。当钢轨磨损严重,可能出现轨侧直线磨损变短,A′点下移,导致轨侧直线中点Z也随之变动。相比于A′点,由于钢轨磨损产生形变,Z点受钢轨磨损的影响更小。而线激光采样的有效轮廓包含轨头、轨腰、轨底三基元,其采样数据在轨颚处必然出现明显间断特征。以轨侧直线中点Z、轨颚点A、轨腰起点B为特征点,对轮廓进行配准,见图1(c)。
1.2 复杂线路轮廓介绍
实际铁路线路复杂多变,主要分为普通轨道区、接头区、道岔区。其中,普通轨道区占线路总长比例最大,正常情况下采样到的普通轨道区,包含有完整的轨头、轨腰和轨底基元,基于轨腰双圆心拟合、轨侧直线配准、刚体ICP配准,具有相对高的配准精度,能够较为准确地计算出钢轨磨耗值。但由于车体振动,障碍物遮挡,列车驶入接头区、道岔区等特殊线路区域等情况,可能导致采集到的钢轨轮廓数据异常。复杂线路不同区域的钢轨轮廓形态见图2。

图2 复杂线路不同区域的钢轨轮廓形态
图2中,数据缺损或变形严重的钢轨轮廓,无法准确计算钢轨磨耗值,通常可直接去除。但当轨头部分数据正常,只是轨腰轨底部分数据变形或缺损时,同样也能准确计算出钢轨磨耗值。然而由于数据缺失,传统的配准方法通常无法准确进行校准,只能将此类钢轨轮廓分为异常无效数据清除,而本文所提方法能有效配准,避免数据浪费。
2 配准方法
2.1 算法原理
基于二维激光位移传感器车载式钢轨磨耗检测装置,采样得到钢轨轮廓二维点云数据。先对其中值滤波,再判别其有效性。当轨头位置数据完整时,一般可认为其为有效轮廓。标准轮廓对应的采样数据见图3。图3中,纵、横坐标分别是在2D激光位移传感器量程范围内接收到的被测物反射回的二维点坐标,纵坐标为直线距离,横坐标为测量宽度。

图3 标准轮廓采样数据
车载检测时,传感器装于车底,在轨道内侧从斜上方投影获取钢轨轮廓信息,AB段的轨颚区被遮挡,所以采样轮廓在AB段会出现间断。由于设备自身影响以及复杂的检测环境等因素,二维激光位移传感器采集到的钢轨轮廓数据中,点B必然存在波动,所以采样到轮廓数据范围也会有所差异。
得到有效轮廓之后,利用轨颚点处曲线间断的特征和Ramer多边形逼近算法[20]定位到点A′、A。求得轨侧直线A′A的中点Z,通过Z、A、B进行匹配,以轨颚点A为旋转中心和平移对应点,通过采样轮廓Z、B和标准轮廓Z、B在同一坐标的相对位置判别旋转方向。通过差分进化算法进行迭代,选取采样轮廓正常的轨腰段作为相似度度量段。以采样轮廓轨腰间断点B和采样轮廓多边形逼近法求得的点C作为度量段重合区的起止点(每幅采样轮廓的轨腰覆盖范围不固定,且可能存在轨腰被遮挡,数据点缺失等情况,点C位置不固定);以采样轮廓的BC段与标准轮廓求得的相对应的BC段为匹配基元,以采样轮廓BC段各点至标准轮廓曲线的最近距离的均值为约束条件,直至迭代结束,选出最优配准的旋转角度。算法流程见图4。

图4 DE算法迭代旋转配准流程
2.2 配准流程
2.2.1 二维数据配准
基于激光位移传感器磨耗检测系统,传感器相对钢轨的照射角度一般取45°进行数据采集,采样得到的钢轨轮廓数据为二维点云数据。假设得到的二维点云数据由n个点组成,坐标为(xi,yi),i=1,2,…,n,设采样轮廓轨颚点A′、标准轮廓轨颚点A的坐标分别为(xsa,ysa)、(xst,yst),则
(1)
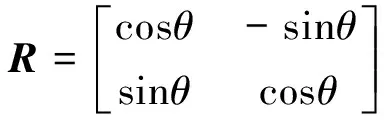
2.2.2 DE算法
DE算法也称差分进化算法,是1997年由Storn等[21]提出的一种基于群体差异的进化计算方法,主要参数有种群大小Np、缩放因子F、交叉概率CR。本文从实际问题出发,以采样轮廓特征曲线位置的点至参考轮廓曲线最近的欧氏距离的平均值为约束条件,通过采样轮廓和参考轮廓特征点的相对位置控制迭代方向,寻求最优R。
在差分进化算法迭代寻求最优R时,以sinθ为个体的定义,传感器采样的照射角度为初始旋转角度,则sinθ起始值Sin=sin45°,每次旋转角度范围为(0,30°),即Sin的范围为(0,0.5)。轨颚具有间断特性,非常容易定位。所以,以采样轮廓轨颚间断点A为采样轮廓的旋转中心点,以求得的采样轮廓轨侧中点Z和轨腰间断点B相对标准轮廓对应的点Z、B的位置判别每次迭代的旋转方向。设测量轮廓点、标准轮廓点Z的坐标分别为(xsa1,ysa1)、(xst1,yst1),测量轮廓、标准轮廓点B的坐标分别为(xsa2,ysa2)、(xst2,yst2)。当xsa1>xst1且xsa2
差分进化算法(DE)迭代配准的具体步骤如下:
Step1设定DE的算法参数。迭代次数为Gm,种群大小为Np,变异概率F0=0.5,交叉概率CR=0.9,只需求得sinθ。根据三角函数性质可以确定旋转矩阵R。所以个体的定义为:正弦值sinθ,数据维度D=1,其范围为(0,0.5)。
Step2随机产生初始种群M,种群大小为Np,即随机产生Mi,j,i=1,2,…,l,…,p,…,q,…,Np,j=D=1。
进入循环G=1,2,…,Gm。
Step3变异操作。
①从M中随机选择3个不同的Mi,i=l,p,q;i≠p≠q。
②对Mi进行变异,计算缩放因子F。
β=exp[1-Gm/(Gm+1-G)]
(2)
F=F0·2β
(3)
③产生变异个体si。
si=Ml+F·(Mp-Mq)
(4)
且要保证变异的个体,其维度依然在(0,0.5)范围内。
Step4交叉操作。设交叉后的种群为Ui,rand为随机产生(0,1)的数据。由于本文方法个体维度为1,所以不需要对个体的各个维度进行判断是否需要进行交叉,只需要判断rand>CR是否成立,如果成立,则当前交叉后的个体为Ui=Mi;否则Ui=si。
Step5旋转方向选择操作。在Step6中经过上一代迭代之后,在种群中选出的最优旋转角度,对测量轮廓进行旋转。根据采样轮廓Z、B两点相对标准轮廓对应点的位置。判断本次迭代旋转方向,见图5。
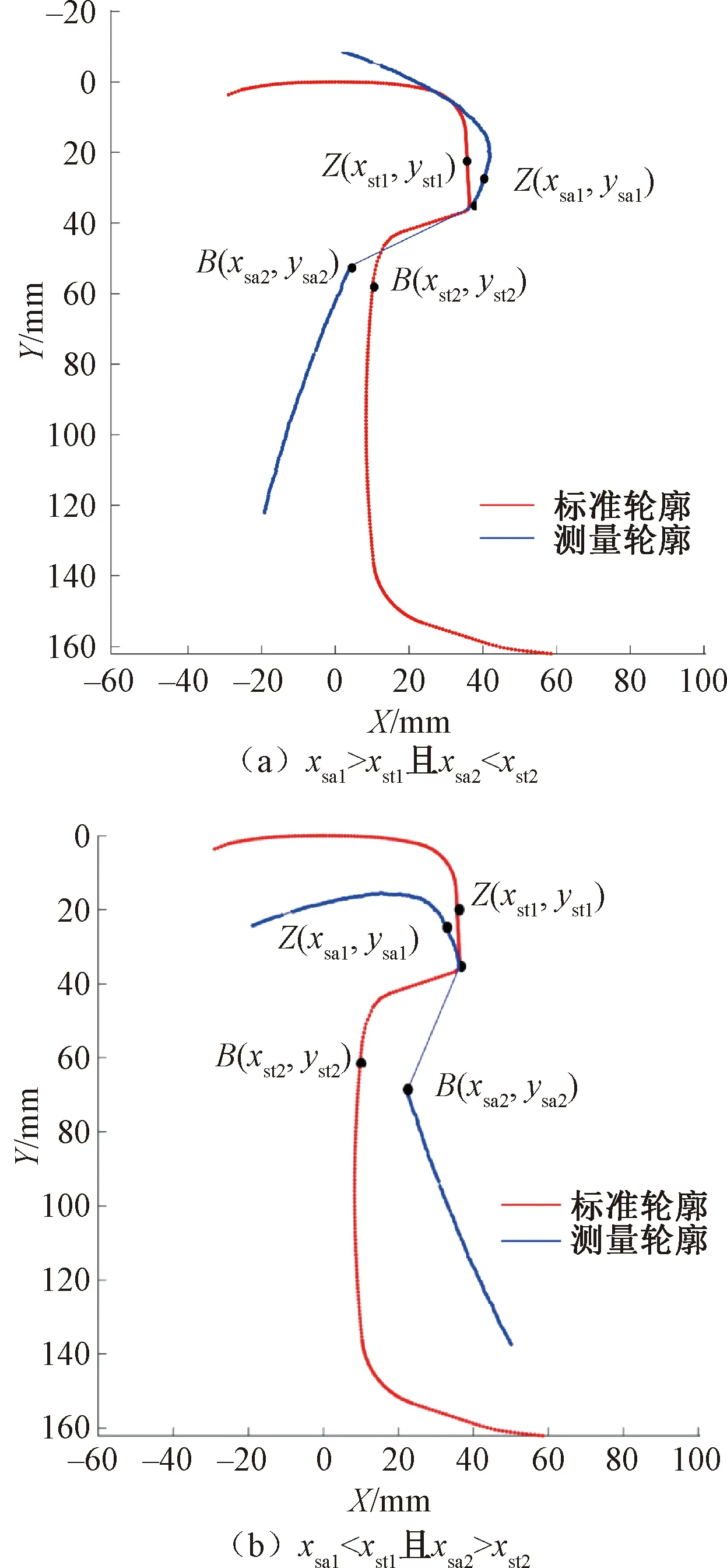
图5 轮廓旋转
由图5可知,当xsa1>xst1且xsa2
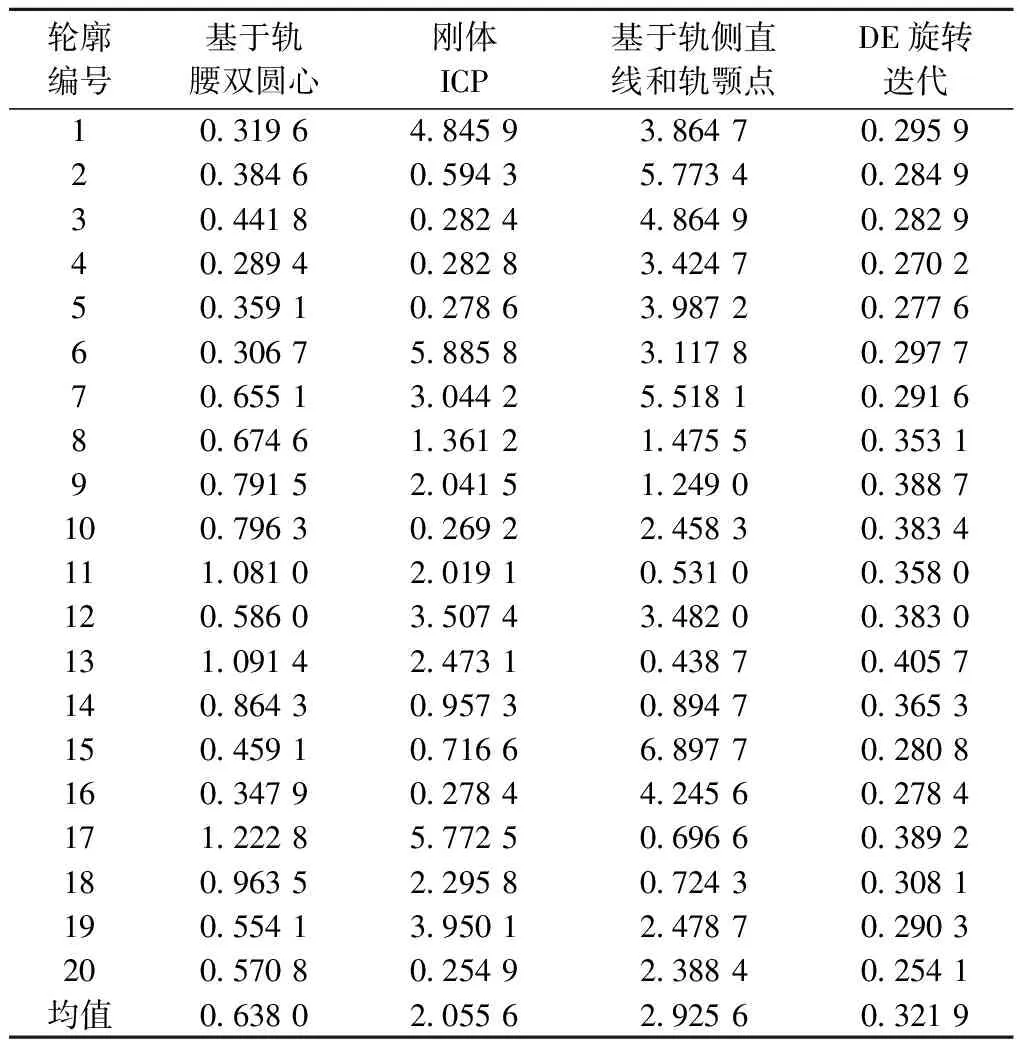
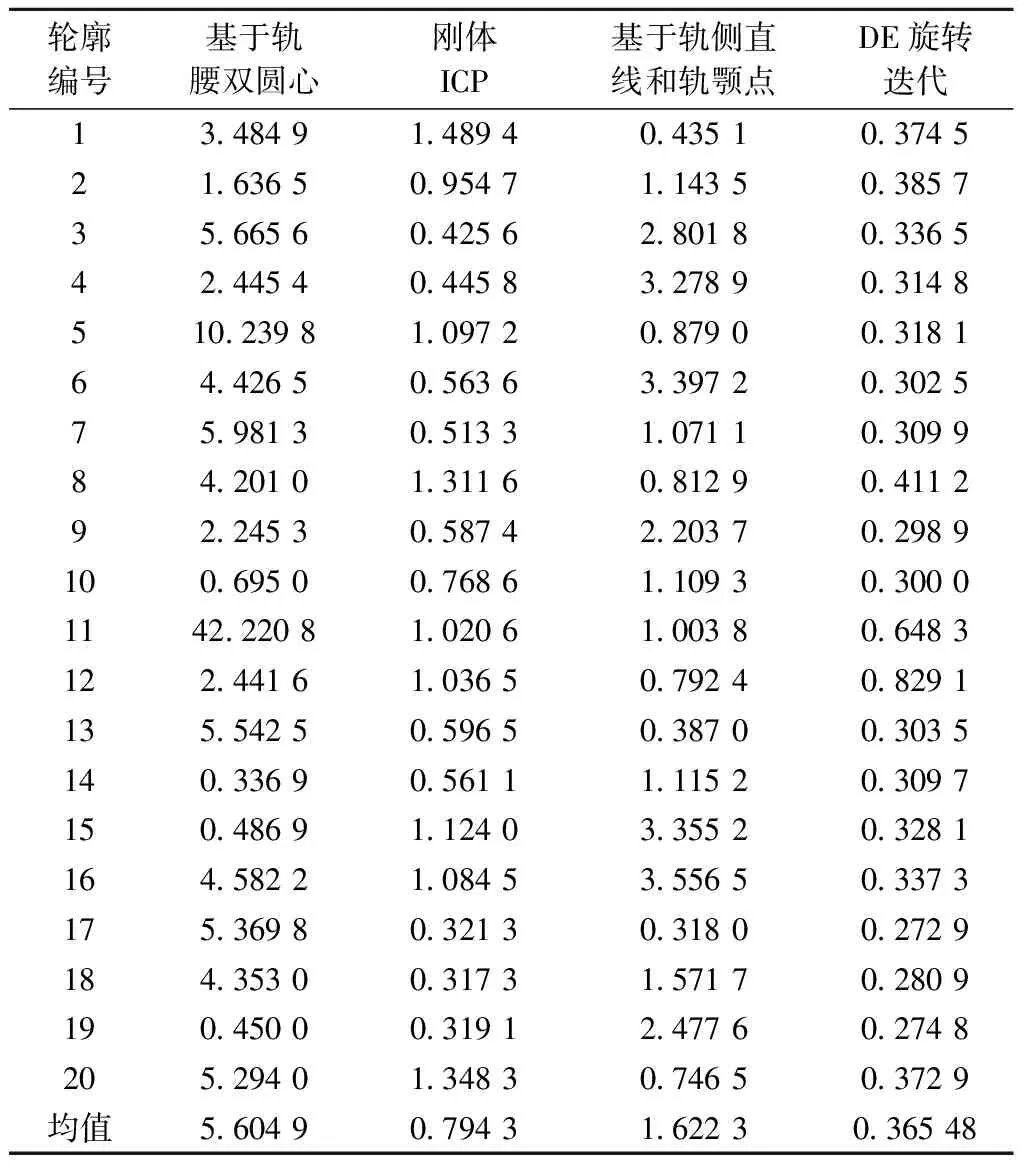
由于测量轮廓变形或者加工精度等影响,实验中发现可能会出现可能存在xsa1>xst1且xsa2>xst2,这时也应该对其顺时针方向旋转Sin=Sin+Ui;xsa1 Step6选择操作。计算新的Sin中每一个个体的适应值,即通过求得的Sin中每一个个体sinθ,求得对应的旋转矩阵R,利用旋转矩阵旋转后,本文以采样轮廓轨腰起点B和以多边形逼近算法Dmax=0.6 mm为阈值,多边形逼近法求得的正常轨腰段终点C之间的数据段作为采样轮廓和标准轮廓匹配重合区;计算重合段采样轮廓各点到标准轮廓曲线的最近欧式距离,求得平均值。找出使得平均值最小的个体,即本代种群中最优的旋转角度,将其保留给Sin做下一次迭代时计算Step5。 Step7选择最优值,迭代结束。通过对比每一代最优角度值对采样轮廓旋转后,采样轮廓的匹配重合区BC段各点至标准轮廓曲线最近距离的平均值,选出所有代中的最优值,即为最终结果。 轮廓精准配准见图6。 图6 轮廓精准配准 由图6可知,本文通过多边形逼近法定位点C,以及BC段重合区做匹配,有效避免了特殊轨形在轨腰数据异常时无法准确配准,导致磨耗检测不准确的情况。 采用基于真尚有公司的高精度2D激光位移传感器设计的车载式钢轨动态检测系统,在10 幅/m的频率下进行轮廓数据采集,采集后的数据统一传输给车载工控机进行处理,并保存数据。 实验数据来自车载式钢轨动态检测系统对100 m长钢轨采集的1 000幅有效钢轨轮廓真实数据。其中,包括800幅正常轮廓数据,200幅轨腰异常轮廓数据。分别从两个方面对本文所提方法的高精度和普适性、鲁棒性进行论证:①配准精度实验,对比不同方法对相同正常轮廓样本数据进行配准后的精度;②点云数据丢失实验,对比不同方法对点云数据缺失的异常轮廓样本数据进行配准。 从车载式钢轨动态检测系统采样到的有效钢轨轮廓数据中,随机选择20幅有效轮廓,分别使用基于轨侧直线和轨颚点配准方法、传统的轨腰双圆心拟合配准方法及刚体ICP配准方法与本文方法配准后的均方误差统计(MSE)结果进行对比,其值越小,精度越高。配准后的均方误差为 (5) 式中:(xsak,ysak)、(xstk,ysak)分别为待配准的测量轮廓和标准轮廓的坐标。 选取20幅正常钢轨轮廓数据,比较4种不同的配准方法。本文以第19、20幅钢轨轮廓的配准效果为例进行展示,见图7。对比结果见表1。 表1 不同配准精度实验MSE结果对比 mm 图7 第19、20号正常数据在不同配准方法中配准效果对比 由图7可知,正常轮廓数据配准时,刚体ICP算法的配准效果十分不稳定,具有很大的跳变性。这是由于其非常依赖于二维点云的初始位置,且要求测量轮廓与标准轮廓的曲线覆盖范围基本一致。当测量轮廓与标准轮廓廓形接近时,配准精度高;存在差异时配准精度低。基于轨侧直线和轨颚点的配准算法,其配准精度整体表现不佳。基于轨腰双圆心的配准算法,精度相对较高。数据正常时,与刚体ICP算法相比,受测量轮廓廓形影响较小,配准效果较为稳定。但是与上述3种方法比较,本文所提DE旋转迭代算法,配准精度更高,稳定性更好,且对测量轮廓的曲线和特征点要求较低,算法更具鲁棒性。 从采样到的数据缺失轮廓中随机选择20幅异常轮廓,同样采用4种方法分别进行配准,见图8。根据均方误差统计(MSE)结果,比较在数据缺损的情况下各个配准方法的性能,结果见表2。 表2 点云数据丢失实验MSE结果对比 mm 图8 7号数据缺损在不同配准方法对比 由图8、表2可知,当钢轨轮廓轨腰和轨底被遮挡,或是从特殊区域(道岔等)采样到的变形、数据缺损轮廓数据时,基于轨侧直线和轨颚点的配准算法稳定性较强,但是其配准精度始终较低。基于轨腰双圆心的配准算法,因为在轨腰缺损时失去配准基元,导致其配准性能的急剧恶化,甚至无法配准。刚体ICP算法的配准效果也同样受到了轮廓点云数据缺损的影响。在实际应用过程中,这3种配准方法的鲁棒性都有所欠缺,影响真实磨耗值的计算。而本文所提方法,当点云数据缺损时,通过多边形逼近算法求得正常的轨腰段BC和轨腰终点C,其配准效果依然保持较高精度和较好的鲁棒性,表现出优越的抗干扰能力,具有非常重要的工程应用价值。 本文提出基于DE旋转迭代配准技术,通过大量实验以及研究表明,轨腰双圆心拟合以及刚体ICP和基于轨侧直线等配准方法,都存在着自身配准精度低或是对轮廓数据要求非常高,鲁棒性不足等缺点。本文方法不管是数据是否正常,配准精度都非常高且非常稳定。由此可知其精度和抗干扰能力具有很大的优势,具有高鲁棒性。而且,本文方法应用简单,工程应用价值更高,有利于钢轨磨耗动态检测技术的进步以及推广。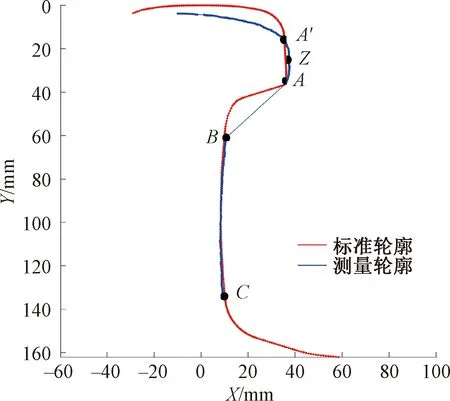
3 实验与仿真
3.1 实验平台及数据采集
3.2 配准精度实验

3.3 点云数据丢失实验

4 结论
