新建隧道下穿施工引起既有铁路轨道变形的理论计算模型

张丙强，刘 海，罗才松

(1.福建理工大学 土木工程学院，福建 福州 350118；2.地下工程福建省高校重点实验室，福建 福州 350118)

随着城市地铁网的扩大,受城市用地限制,地铁隧道近距离下穿既有铁路线路工程将越来越多[1]。新建隧道施工将引起周围土层移动,导致上覆既有铁路路基产生沉降。当路基不均匀沉降发展到一定程度,将造成严重的轨道不平顺,加剧轮轨相互作用,进而降低旅客乘车舒适性[2]。因此,研究新建隧道下穿施工引起上覆既有铁路轨道变形具有重要的工程意义。

目前,对新建隧道下穿对既有铁路线路的影响进行了一些研究。文献[3-4]通过现场监测数据分析,研究了铁路线路地面沉降的发展历程和沉降槽特征等。文献[5-6]采用数值方法,对注浆加固、施工参数等控制地表变形进行了分析。文献[7-8]建立轨道-路基-隧道耦合模型,分析隧道施工对既有线路轨道结构的影响。文献[9]通过室内1∶1模型试验,分析了轨枕空吊前后余弦型路基沉降与轨道变形之间的互相关系。在此基础上,文献[10]基于弹性点支承理论模型,提出有砟轨道路基沉降引起轨面变形的计算方法。文献[11]采用考虑层间接触非线性的轨道-路基数值模型,对无砟轨道路基沉降引起轨面变形特征进行了分析研究。

需要指出的是,目前针对隧道下穿施工引起既有铁路钢轨变形的理论研究相对较少。两阶段分析方法由于使用简单而被广泛用于研究隧道开挖对周围环境的影响中,如邻近管线[12-15]、隧道[16-17]、建筑物[18-19]等。第1阶段采用理论方法或经验公式预测隧道施工所引起邻近建筑物所处位置土体的自由变形;第2阶段将邻近管线等视为弹性地基上的梁,采用理论方法分析上述土体自由变形作用下其力学响应。然而,钢轨通过枕木支撑在道床上,当道床发生沉降时,枕木支撑面会随之下沉,轨枕会发生空吊现象[9-11],上述线性弹性地基梁模型不再适用。为此,提出一种可以模拟钢轨局部脱空的计算模型,采用两阶段分析方法对新建隧道施工引起钢轨变形进行求解;进而探讨铁路线路与新建隧道之间的夹角、钢轨抗弯刚度、路基沉降槽宽度等参数对钢轨变形的影响。研究成果将为新建隧道下穿施工引起既有铁路钢轨变形提供理论方法。

1 问题描述及变形控制方程

新建隧道下穿施工引起既有铁路轨面变形的力学分析模型见图1,钢轨脱空区长度为2l。以隧道与铁路相交点为坐标原点,建立如图1所示的坐标系x-y,隧道与轨道的水平面夹角为β。拟采用两阶段分析方法进行求解,并作如下基本假定:

图1 隧道下穿既有铁路力学分析示意

(1)地基土体为均质、各向同性的半无限空间弹性体。

(2)路基顶面沉降包括隧道施工引起竖向自由位移和钢轨与路基互相作用产生的位移两部分组成[14]。

(3)隧道施工引起路基顶面竖向自由位移符合高斯分布[12-13]。

(4)钢轨视为弹性无拉力弹性地基上的Euler梁。

根据弹性地基上的Euler梁理论,建立钢轨挠曲变形控制方程为[14]

(1)

式中:u(x)为钢轨挠曲变形;ErIr为钢轨抗弯刚度;p(x)为钢轨所受外力。

路基沉降将改变钢轨所受外力p(x),进而导致钢轨产生竖向挠曲变形。若钢轨挠曲变形大于路基顶面沉降,则轨枕与道床仍然保持接触,此时轨道所受荷载为道床对轨道的反力;否则轨枕与道床将产生分离,发生轨枕空吊现象,此时轨道所受荷载等于轨枕自重。新建隧道下穿施工引起钢轨所受荷载为

(2)

式中:q为轨枕的重量;ks为轨枕支承刚度系数;w(x)为钢轨与路基互相作用产生的路基沉降;s(x)为隧道斜交下穿引起路基顶面竖向自由位移,可采用高斯分布函数进行描述[12-13]

(3)

其中,Vt为隧道施工引起的平均地层损失比;Rt为隧道开挖半径;is为路基顶面沉降槽宽度系数,可采用is=κzt进行计算,κ为地层沉降槽宽度参数,zt为隧道中心到道床底面的竖向距离。

将式(2)代入式(1),得到新建隧道下穿施工引起铁路钢轨变形计算的控制方程为

2 控制方程解析方法

由于计算模型具有对称性,取右半部分进行分析,并将钢轨在脱空段与接地段的分界处切断。令x1、x2分别为脱空段、接地段局部坐标;u1、u2分别为脱空段、接地段轨道变形。脱空段为长度为2l的短梁,接地段为Winkler地基上的半无限长梁。两段钢轨的受力示意见图2,MA和QA分别为分界处截面所受弯矩和剪力。

图2 钢轨力学分析示意

2.1 脱空段的求解方法

根据Euler梁挠曲变形理论,可得到关系[20]式

(5)

式中:M(x1)、Q(x1)为钢轨截面所受弯矩和剪力。

对式(4)依次进行一次、二次和四次积分,并联合式(5)及边界条件

可得脱空段钢轨挠曲变形为

(6)

式中:A、B为待定参数,可由边界条件确定。

根据模型对称性,脱空段中点及端点条件为

(7)

(8)

2.2 接地段的求解方法

接地段钢轨变形为端点弯矩MA、剪力QA和分布荷载kss(x2+l)分别作用下产生的挠曲变形之和。根据弹性地基梁理论,接地段钢轨挠曲变形控制方程对应的齐次方程的通解为

u2=e-αx2(Ccosαx2+Dsinαx2)

(9)

式中:C、D为待定参数,可由边界条件确定。

端点作用外力时边界条件为

(10)

将式(10)代入式(9),得到端点弯矩、剪力作用下钢轨挠曲变形为

(11)

分布荷载kss(x2+l)作用下接地段钢轨挠曲变形为

(12)

[cos(α|x2-x′2|)+sin(α|x2-x′2|)]dx′2

(13)

其中,x′2为计算点位置。

为此,接地段钢轨挠曲变形为

u2=u2A+u2B

(14)

式(8)、式(14)中的未定参数可由下列连续条件确定,即

(15)

根据上述连续条件,求出待定系数为

(16)

2.3 计算流程

式(8)、式(14)和式(16)中钢轨与道床脱离区长度2l是未知的,因此无法直接求解,本文将采用逐次逼近法进行求解。首先初步假定一个脱离区长度值2li,通过求解得到钢轨挠曲变形和道床顶面沉降值;然后通过比较钢轨挠曲变形与道床顶面沉降曲线,确定一个修正的脱离区长度值2li+1;重复以上过程,直到两次计算得到的脱离区长度非常接近为止。具体计算流程见图3。

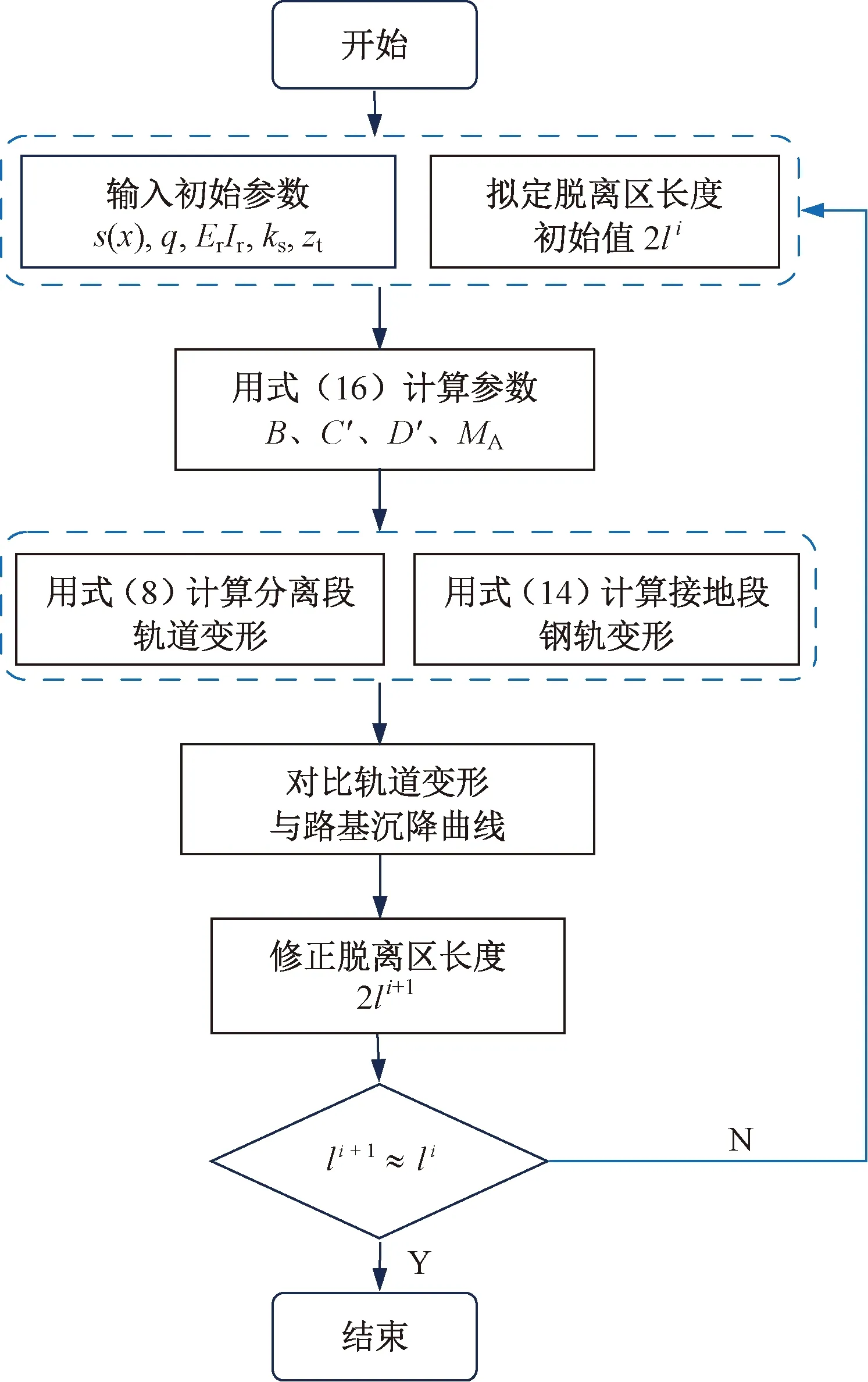
图3 计算流程图

3 本文方法的验证

3.1 与模型试验结果对比

文献[9]设计了长为12.5 m的有砟铁路模型试验系统,线路采用60钢轨、钢筋混凝土Ⅱ型轨枕、Ⅲ型弹条扣件,列车荷载采用激振设备模拟。通过模型试验,研究轨枕空吊前后,路基沉降与轨道变形的相互关系。采用本文方法对文献[9]中工况二和三进行计算,钢轨抗弯刚度ErIr=6.624×103kN·m2,轨枕支承刚度系数ks=6.7×104kN/m,轨枕自重荷载q=6 kN/m。计算结果与模型试验数据对比见图4,图中,Am为路基沉降最大值。由图4可知,两者吻合程度较高。

图4 本文计算结果与试验数据对比

3.2 与现场监测数据对比

文献[10]提供某区间隧道下穿铁路线引起路基及轨道变形进行了现场监测数据,隧道开挖直径为6.2 m、平均埋深为12 m,线路与隧道间的水平夹角为88°。采用余弦函数对路基现场监测沉降数据进行拟合,并基于连续弹性点支承梁模型的计算方法对路基不均匀沉降引起轨道的变形进行计算,见图5。为进一步验证理论方法的正确性,采用本文方法对该工况进行计算,模型中钢轨抗弯刚度取ErIr=6.624×103kN·m2,地基系数取ks=6.7×104kN/m。现场监测结果、文献[10]理论计算结果以及本文计算结果对比见图5。由图5可知,三者吻合程度较高。

图5 本文方法与现场监测数据对比

4 参数分析

4.1 钢轨抗弯刚度的影响

增大钢轨抗弯刚度以抵抗地基沉降的影响,是控制隧道下穿施工引起上方轨道变形影响的常用措施之一。当铁路线路与新建隧道成垂直相交时,新建隧道下穿施工引起轨道挠曲变形曲线随着钢轨抗弯刚度变化情况见图6。算例中路基沉降最大值smax=10 mm,路基顶面沉降槽宽度is=3 m,钢轨抗弯刚度ErIr=6.624×103kN·m2,轨枕支承刚度系数ks=6.7×104kN/m。

图6 钢轨抗弯刚度对钢轨挠曲变形的影响

由图6可知,随着钢轨抗弯刚度的增大,钢轨挠曲变形幅值逐渐减小,但是钢轨变形波长基本保持不变。当钢轨抗弯刚度ErIr增大到4倍时,路基沉降槽中心正上方局部轨枕产生空吊现象。当钢轨抗弯刚度增大从1倍增加到10倍时,钢轨挠曲变形最大值从10 mm减小到8.4 mm。由此可见,增大钢轨抗弯刚度可以控制隧道下穿施工引起上方有砟铁路钢轨挠曲变形幅值,但效果不够明显。

4.2 路基沉降槽宽度的影响

路基沉降量最大值smax及沉降槽宽度系数is是隧道下穿施工引起的铁路路基顶面沉降的两个重要参数,并且smax与is密切相关。当铁路线路与新建隧道线路成45°斜交时,钢轨挠曲变形随着新建隧道下穿施工引起路基沉降槽宽度系数的影响见图7,算例中其余计算参数同4.1节。

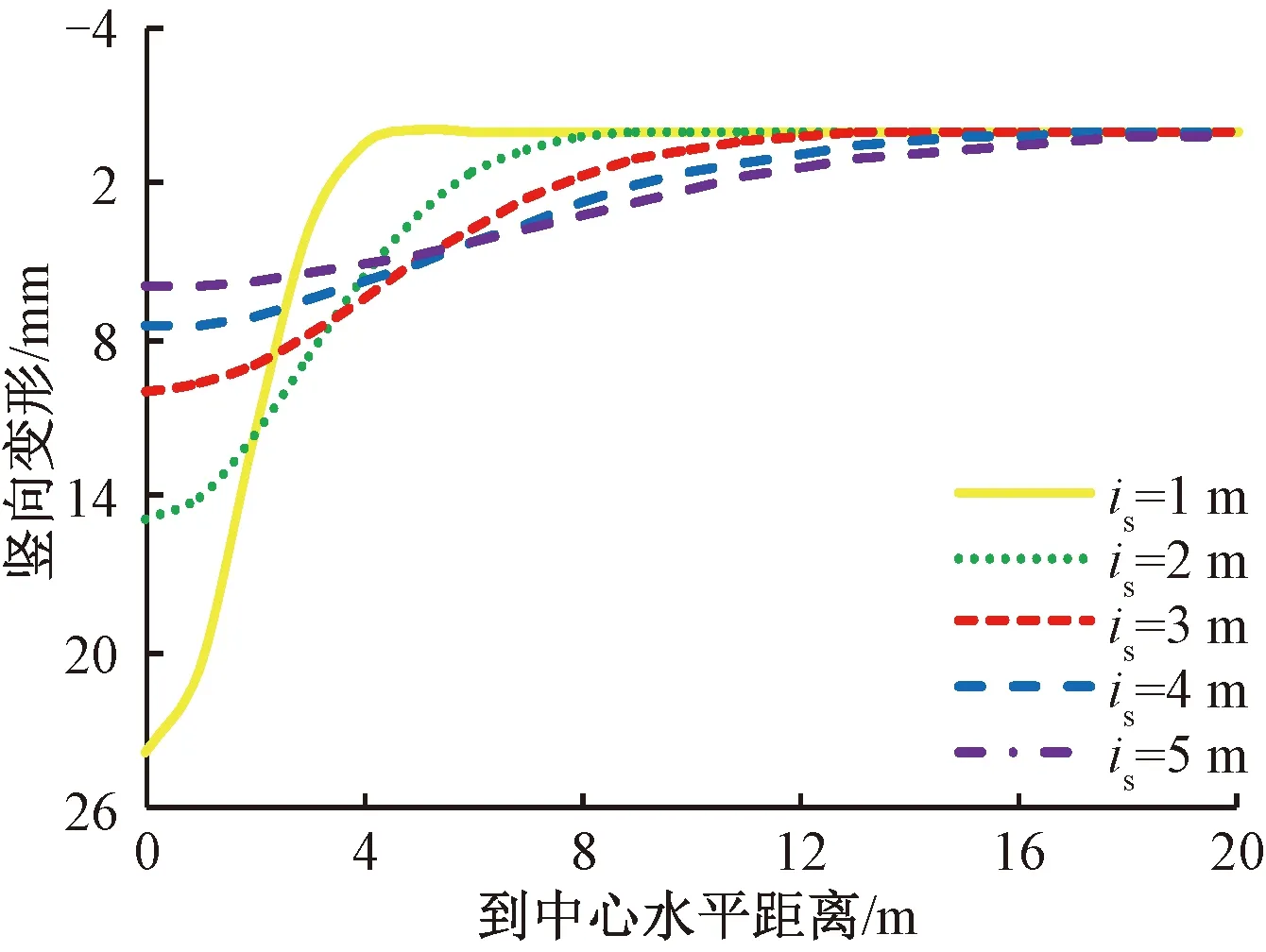
图7 路基沉降槽宽度的影响

由图7可知,随着路基沉降槽宽度系数的增大,钢轨挠曲变形幅值逐渐减小,而且变形波长逐渐增大。当路基沉降槽宽度系数is小于2 m时,路基沉降槽中心正上方轨枕会产生空吊现象。当路基沉降槽宽度is从1 m增加到5 m时,钢轨挠曲变形最大值从24 mm减小到5 mm,波长从约8 m增加到48 m。由此可见,增大路基沉降槽宽度系数可以有效控制隧道下穿施工引起上方轨道挠曲变形影响。

4.3 隧道与铁路相交角度的影响

新建隧道与既有线路之间的水平夹角是影响隧道施工引起路基顶面沉降的另外一个重要参数。为分析新建隧道斜穿角度对钢轨挠曲变形的影响规律,分别计算不同下穿角度条件下钢轨挠曲变形,具体结果见图8,算例中计算参数同4.1节。

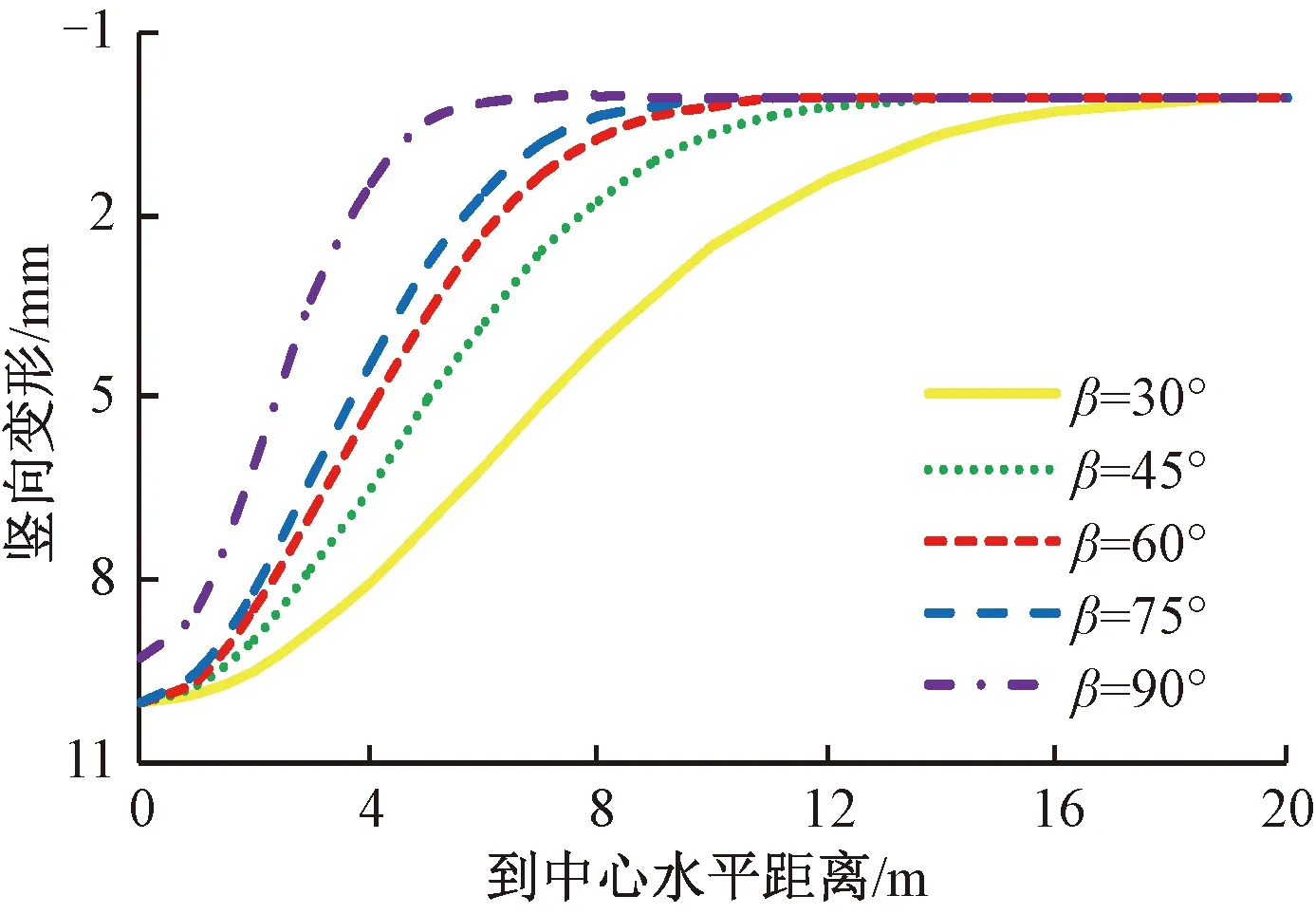
图8 隧道与铁路相交角度对钢轨挠曲变形的影响

由图8可知,随着新建隧道与铁路线路间水平夹角的逐渐增大,钢轨挠曲变形波长逐渐减小,但钢轨变形幅值略有减小。当铁路线路与新建隧道成垂直相交时,路基沉降槽中心正上方轨枕会产生空吊现象。当水平夹角β从30°增加到90°时,钢轨变形波长从48 m减小到8 m。由此可见,选择大角度穿越既有铁路是控制隧道下穿施工引起钢轨挠曲变形波长的有效措施之一。

5 结论

(1)针对路基不均匀沉降可能导致有砟铁路轨枕产生空吊现象,提出采用无拉力弹性地基模拟钢轨与路基相互作用,并根据钢轨与路基相对变形判别两者的接触状态,从而建立新建隧道下穿施工引起既有铁路轨道变形理论计算模型。

(2)将钢轨分为左、右两侧半无限长接地段与中间脱离段共三部分分别求解钢轨挠曲变形,并通过与室内模型试验结果和现场监测数据对比进行了验证。进而探讨了钢轨抗弯刚度、路基沉降槽宽度系数以及铁路与新建隧道间的水平夹角对钢轨挠曲变形的影响规律。

(3)本文计算条件下,当路基沉降槽宽度系数小于2 m时,新建隧道垂直下穿施工将导致上方有砟铁路轨枕产生局部空吊现象。增大钢轨抗弯刚度,可以减小钢轨挠曲变形幅值;增大铁路线路与隧道之间水平夹角,可以减小钢轨挠曲变形波长;增大路基沉降槽宽度系数,轨道挠曲变形幅值逐渐减小,并且波长逐渐增大。