基于LSTM动态波束赋形的高速列车越区切换算法
2023-11-06李翠然张泽鹏谢健骊
李翠然,张泽鹏,谢健骊
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
铁路运输具有运载能力大、运行速度快、运输效率高等特点。铁路通信系统是铁路运输的“动脉”,但高速铁路(以下简称“高铁”)列车运行环境复杂[1],主要场景有平原、山地、丘陵、城郊,经过的特殊地貌有高架桥、路堑、隧道等。由于场景的复杂性以及列车的高时速,多径衰落、多普勒频移、高车厢穿透损耗和复杂场景中移动中继节点(Mobile Relay Node,MRN)接收信号质量差导致的越区切换中断概率高等技术问题一直难以解决[2-4]。如何设计合理的越区切换算法,有效提升高铁用户服务质量和服务体验是亟待解决的关键问题。
为了解决高铁运行场景中“越区切换中断概率高”的问题,相关学者展开了大量研究。米根锁等[5]提出基于速度的提前切换算法,在切换前执行信令交互并设置预承载点,改善过早或过晚切换带来的通信中断、掉话等问题,但未考虑所提算法与基站硬件设备性能的结合问题,仿真环境较为理想化。为了减少切换中断时间,李东航[6]针对多车交会场景提出基于长短期记忆网络(Long Short Term Memory,LSTM)的列车控制与信息服务网络流量预测模型,结合列车的速度位置信息预测列车与eNB间的无线通信数据传输速率,并提前为基站覆盖区内的列车做好功率分配,从而提高切换带内的信号强度,帮助列车顺利执行越区切换。此算法在实现难度和匹配基站硬件设施方面存在优势,且在不改变基站总功率的前提下能够获得明显的信号增益,因此其已广泛应用于越区切换算法中。波束追踪能够根据终端移动性,以较高的灵活性来调整波束方向以跟踪特定的传播路径,从而实现较低的中断概率和最优的速率容量性能[7]。朱豪等[8]针对列车在基站重叠区切换触发概率和切换成功率均较低的问题,基于遗传算法提出一种自适应联合判决切换策略,该文主要针对开阔地场景。传统的LTE-R切换方案由于忽略了列车经过eNB重叠区的时间导致列车错过最佳切换点。文献[9]提出基于贝叶斯算法的回归预测模型,通过预测列车经过重叠区边缘的过境时间,提前触发切换,提升了切换效率和切换性能,但缺乏对算法复杂度的分析。高铁无线信道中的电波传播有其特殊性,运行场景不同则接收信号功率和阴影衰落也存在差异。上述文献建模过程均未考虑路堑等特殊地形下信号遮蔽、信号非视距传输等现象[10]。此外,忽略了不同高铁地形以及周围植被、障碍物的反射、散射信号的衰落差异性对越区切换性能的影响。
针对上述问题,本文以典型高铁地形(路堑、高架桥)作为研究场景,对路堑地形环境下存在的信号遮挡现象展开分析,利用LSTM对时间参数序列的预测能力和动态波束赋形追踪策略,提出基于LSTM预测的动态波束赋形越区切换算法。所提算法通过来波到达角(Direction of Arrival,DoA)辅助车载全球导航卫星系统(Global Navigation Satellite System,GNSS)确定列车位置,由基于LSTM神经网络预测及增加了预留角的动态波束对MRN进行对准追踪,从而提高eNB覆盖区边缘MRN的接收信号功率。并提出中断概率阈值参数k和eNB总功率Pa联合约束的波束增益分配算法,达到合理分配eNB功率、降低切换中断概率、提高切换触发概率和切换成功率的优化目标。
1 系统模型与运行场景
1.1 中继通信模型
高铁线路中继通信系统模型见图1。图中,eNB发射天线向部署于高铁列车车顶的MRN发送信号,MRN再将信号传送给列车上的用户,该方法能够避免信号穿过车体产生的穿透损耗。假设eNB天线采用全向天线模式,eNB覆盖半径为r,相邻eNB间距为Dab,则重叠区宽度为2r-Dab。图1中,点P、Q、R分别表示eNB重叠区的起点、中点和终点。当列车以速度v从源小区eNBa向目的小区eNBb行驶时会发生越区切换,切换触发准则为[11]:若某一时刻列车接收到eNBb的信号功率大于eNBa,且两者差值大于或等于触发门限Γ时触发切换,否则列车仍保持与eNBa的通信。当eNB配备智能天线时,基于定向波束赋形技术能够动态跟踪MRN位置,使MRN始终处于波束主瓣内,以解决由于较低触发门限引起的乒乓切换以及列车高速运行引起的多普勒频移和车厢穿透损耗等问题。

图1 高铁线路中继通信模型
1.2 运行场景
高铁运行场景被分为平原、高架桥、路堑等12种,不同地形的信道参数差异很大。视距路径(Line of Sight,LoS)的概率计算式为[12]
(1)
式中:dx为eNB与MRN的通信距离;dbp为断点距离;α为衰减参数。
图2为两种典型场景下的LoS概率曲线。
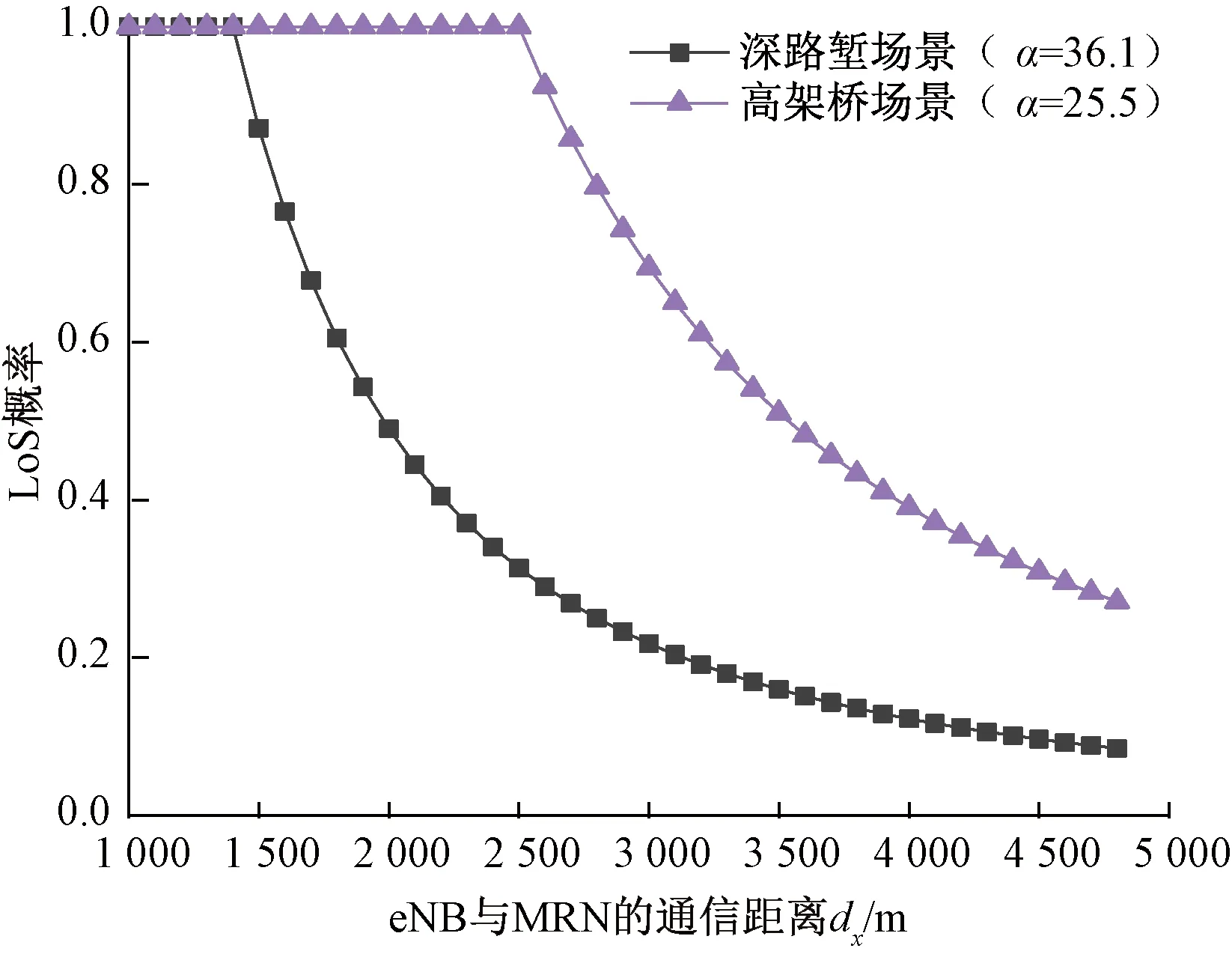
图2 两种场景下的LoS概率
由图2可见,高架桥场景下LoS概率均值比深路堑场景下LoS概率均值大。其原因是高架桥场景下,MRN位于离地面10~30 m的高架桥上,桥面较高且轨面高度恒定,eNB与MRN之间的LoS传播受障碍物的影响较小;而路堑场景下尤其是深路堑时可能存在遮挡现象,导致无线路径被障碍物阻挡[13]。
路堑地形作为典型的遮挡场景,若使eNB发射的信号波束能够无遮挡地到达MRN处,eNB天线高度需满足一定的约束条件。图3给出了路堑场景中的遮挡情形示意图,假设路堑结构近似为平行,不存在拐弯、曲折情况。

图3 路堑场景的遮挡情形示意
图3(a)中,eNB天线波束赋形的发射点记为p,MRN接收点记为q。H1、H2、h和d分别为eNB天线高度、路堑边坡高度、MRN距离地面的高度和eNB底端与铁轨之间的距离。路堑底部宽度为Wdown,MRN与y轴的垂直距离为DS,路堑边坡倾角γ较小,计算时可忽略。建立三维直角坐标系,点p、点q的坐标分别表示为(x1,y1,z1)=(0,-d+Wdown/2,H1+H2),(x2,y2,z2)=(-DS,Wdown/2,h)。图3(b)中,l1,l2,…lj分别为各个方向基站发射波束的主瓣中心线,假设li为eNB天线波束恰好掠过路堑边坡、无遮挡到达MRN的主瓣中心线,则直射线pq对应的三维空间参数方程可表示为
(2)
为保证eNB发射波束能够无遮挡到达MRN处,则直射线上的点应满足
(3)
结合空间直线参数方程,得到eNB天线高度的约束条件
(4)
式中:X为列车行驶距离,取值无约束;ε为任意实数。
2 基于LSTM的动态波束赋形策略
2.1 改进的动态波束赋形
传统的基于波束赋形的越区切换技术在eNB重叠区内的波束增益为固定值[14],未能较好地考虑列车在重叠区内移动时其接收功率随距离变化对波束赋形增益的影响。为此,提出基于位置辅助的动态波束赋形机制,通过估计MRN的DoA,使eNB发射信号功率集中在波束主瓣方向,旁瓣信号强度近似为零,以达到抑制干扰、提高越区切换性能的目的。图4为动态波束赋形的DoA模型。图4中,假设列车在eNB重叠区的行驶轨迹为直线,令列车顶部的MRN位于x位置处(由车载GNSS提供位置信息),则波束下倾角αx,波束主瓣宽度θx分别表示为
(5)
(6)
式中:H为eNB顶端距离地面的高度;dmin为eNB顶端和铁轨之间的距离,表示为
(7)
列车进入重叠区后,eNBb开启波束赋形模式,使波束主瓣方向指向MRN并随其变化,见图5。当MRN位于x位置时,Dab-r≤x≤r,eNBa波束主瓣宽度θa和eNBb波束主瓣宽度θb分别为

图5 改进的波束赋形覆盖方式
(8)
(9)
式中:θmax和θmin分别为波束主瓣宽度角θa(θb)的最大、最小值,其示意见图4。
2.2 动态波束赋形增益
根据信干噪比(Signal to Interference Plus Noise Ratio,SINR)和参考信号接收功率(Reference Signal Receiving Power,RSRP)等切换参数具有较强的时空相关性[6],提出一种基于LSTM的波束增益需求预测模型。首先根据eNB采集的切换参数值,预测eNB与列车间未来时刻的RSRP值序列;其次在满足中断概率阈值参数k和eNB总功率Pa约束条件下,按需为列车补偿满足通信需求的波束增益。同时,结合2.1节的波束主瓣宽度角度估算,优化越区切换算法。
2.2.1 LSTM神经网络基本原理
LSTM整个存储单元由三个激活门(遗忘门、输入门和输出门)控制。三个门和对应单元信息的更新公式为[15]:
遗忘门:在单元信息更新中控制上一时间步记忆单元的哪些信息被留存。在时间步t中遗忘参数ft的计算式为
ft=σ(Wf[ht-1xt]+bf)
(10)
输入门:在记忆单元完成对信息的遗忘处理后,由输入门决定新的候选向量值有多少参与到记忆单元信息的更新中。其输出参数it表示信息保留的程度
it=σ(Wi[ht-1xt]+bi)
(11)
(12)
(13)
输出门:处理当前记忆单元的状态值并输出。
ot=σ(Wo[ht-1xt]+bo)
(14)
ht=ottanh(ct)
(15)
式中:W为权重矩阵;b为偏置项,表示矩阵元素乘积;ht-1为上一时刻编码器的隐藏状态;xt为待预测序列样本值,tanh为双曲正切激活函数;σ为sigmoid激活函数,定义式为
(16)
(17)
最终预测值由输出层计算式为
yt=σ(Wyht+by)
(18)
2.2.2 基于LSTM的波束增益预测问题建模
当列车行使在eNB重叠区之外时,MRN周期性地对列车RSRP进行采样并上报,eNB得到初始RSRP序列L1:{x1,x2,x3,…,xN};为了提高预测的准确性,利用滑动窗口对L1进行平滑处理,使数据更加平稳。再对L1进行归一化,将其转换为具有固定时间步长的序列集L2:{X1,X2,X3,…,XM},其中X1对应步长为t的RSRP序列{x1,x2,x3,…,xt}的变化情况。基于LSTM神经网络,根据前t个时间步长的测量值实现对t+1时刻的RSRP值的预测,最后得到未来一段时间域内RSRP序列的预测值,由此即可计算出t+1时刻列车所需的波束赋形增益Gt+1。基于LSTM预测和k-Pa联合约束的波束增益预测分配算法为:

输入:dx,L1,k,Pt,Pa输出:Xt+1,Gt+1初始化:dx←1 800;Xt+1←0;Gt+1←0;LSTM设置:dataTrain←90%,dataTest←10%numFeatures = 1,numResponses = 1,numHiddenUnits = 20×3;InitialLearnRate = 0.005,GradientThreshold = 1,LearnRateDropFactor = 0.2; MaxEpochs = 300;mu = mean(dataTrain),sig = std(dataTrain),dataTrainStandardized = (dataTrain - mu) / sig;net = trainNetwork(XTrain,YTrain,layers,options);1:YPred = sig×YPred + mu;2:Xt+1 ←YPred;Gt+1=f2(Xt+1,k)3:while (1 800 =
2.3 波束赋形预留角
高速列车越区切换算法中,当利用车载GNSS提供的MRN位置信息进行波束对准时,系统噪声和传输延迟可能会引起不容忽视的MRN定位误差,从而导致高铁用户掉线和通信中断,通过增加波束预留角可以有效降低切换中断概率[16]。图6所示为定位误差引起的波束赋形角度误差。

图6 定位误差引起的波束赋形角度误差示意
图6中,令Δx为MRN定位误差;Δμx为波束赋形角度误差。Δx与Δμx之间的函数关系式为
(19)

(20)

(21)

3 越区切换算法性能
3.1 不同场景的路径传输损耗模型
路径损耗模型能够预测接收信号强度,为评估列车接收信号质量和越区切换提供理论依据。无线信道的路径传输损耗预测模型可表示为
(22)
式中:PL(d0)为截距;n为路径损耗指数;Xσ为阴影衰落,且服从均值为0的高斯随机分布。路堑、高架桥场景下的路径传输损耗分别为[17]
(23)
(24)
式中:Xσcut、Xσvia分别为路堑、高架桥场景的阴影衰落,服从均值为0的高斯随机分布。
3.2 性能分析
假设eNB发射信号功率为P,当列车经过重叠区时,eNBa和eNBb分别产生不同的波束赋形增益,列车接收到来自eNBa和eNBb的信号功率分别表示为
(25)
(26)
式中:PLa、PLb分别为eNBa、eNBb与列车之间的传输路径损耗;G1、G2分别为2.2节预测得到的源基站、目的基站实际分配的波束增益。由此得到切换中断概率为
Pout(dx)=Pr[Prb(dx)<λ]=
(27)
式中:λ为保证正常通信的最小接收信号功率阈值。
切换触发概率Ptri可表示为
Ptri(dx)=Pr[Prb(dx)-Pra(dx)≥Γ]=
(28)
为保证列车在重叠区内成功切换至eNBb,就要使列车与eNBa、eNBb均保持可靠的通信连接,并顺利触发切换。因此,切换成功率可描述为:切换前与eNBa通信未中断、切换中顺利触发并成功切换和切换成功后与eNBb未中断同时成立。切换成功率Psuc可表示为
Psuc=[1-Pout(dx)a]·Ptri(dx)·[1-Pout(dx)b]
(29)
式中:Pout(dx)a为MRN与源基站a的通信中断概率;Pout(dx)b为MRN与目的基站b的通信中断概率。
4 仿真结果
本文利用MATLAB仿真平台验证越区切换算法性能,仿真参数如表1所示[14]。

表1 仿真参数
图7为当h=3 m,Wdown=6 m,H2取值为2.5~5 m,eNB底端和铁轨之间的距离d取值为10~50 m时,满足发射波束不被遮挡的最低eNB天线高度。可看出,当H2≤h时,eNB天线高度取值无约束;当H2>h时,eNB距离MRN越远,路堑边坡越高,满足波束无遮挡时的eNB天线高度值就越大。这说明,图3(c)所示的浅路堑地形通常不会发生波束被路堑边坡遮挡的现象,深路堑地形可能存在波束被路堑边坡遮挡的情况。波束是否被遮挡与eNB天线高度H1、路堑边坡高度H2、MRN高度h以及eNB底端与铁轨之间的距离d相关。

图7 不同距离下波束无遮挡时的最低eNB天线高度
基于2.2节分析,本文将样本数据的90%输入神经网络进行训练,剩余10%作为测试集。基于LSTM网络训练得到路堑地形下的RSRP预测值与理论值仿真结果见图8。其中,图8(a)中前90%为样本数据,剩余10%为预测结果;图8(b)为样本数据与预测数据的结果对比(注:横坐标180个数据点的对应编号为1620~1800);图8(c)为预测值与样本数据之间的误差变化。由图可知,基于LSTM的RSRP预测值与理论值基本拟合,波动幅度相对平稳,很好地预测了未来时刻接收信号质量的变化趋势,能够满足实际RSRP预测需求。
图9为基于LSTM预测和k-Pa联合约束的波束增益分配结果。图中,点P、Q、R分别表示eNB重叠区的起点、中点和终点。在eNB重叠区内C点(2 114 m)之前,RSRP值较大,eNB无需补偿波束增益就能触发越区切换;C点之后,列车离eNB越来越远,RSRP值减小,eNB需要补偿一定的波束增益才能顺利触发切换;D点(2 915 m)之后,RSRP值降至最低,列车所需的波束增益大于eNB所能补偿的波束增益,eNB只有降低切换触发门限才能保证切换顺利进行。

图9 基于LSTM预测和k-Pa联合约束的波束增益分配


图10 波束赋形预留角
路堑、高架桥地形下的切换中断概率、切换触发概率和切换成功率性能对比曲线分别见图11~图13。其中,路堑场景、高架桥场景分别用Cuttings、Viaduct表示,传统A3切换算法[14]用A3表示,均匀波束赋形算法[14,18]用JY表示,文中提出的动态波束赋形-无预留角算法用DB-NA表示,动态波束赋形-预留角算法用DB-A表示。
由图11可以看出,两种地形下,动态波束赋形-预留角算法的切换中断概率最低,均匀波束赋形算法切换中断概率虽优于传统A3切换算法,但明显低于本文所提算法。这是因为波束预留角策略考虑了MRN定位误差引起的波束赋形角度误差,通过增加波束预留角可以有效降低切换中断概率。其次,在高架桥场景中四种算法的系统性能都优于路堑场景的对应算法,这是因为高架桥场景的LoS概率均值大于路堑场景的LoS概率均值,路径损耗较小。
由式(28)可知,切换触发概率与波束预留角无关,图12对比了两种场景下动态波束赋形-无预留角算法、传统A3算法和均匀波束赋形算法的切换触发概率变化趋势。图中,随着列车从P点移动至R点的过程,三种算法的切换触发概率随之增加,动态波束赋形算法的切换触发概率变化趋势与均匀波束赋形算法相似,但都大于A3切换算法和均匀波束赋形算法。这是因为当列车进入eNB重叠区时,eNB由全向天线模式转为动态波束赋形模式,列车同时接收到eNBa和eNBb事先预测并分配的波束赋形增益,当列车经过Q点之后,eNBa增益减小加速了越区切换的触发,使两种波束赋形算法的切换触发概率急剧增大。

图12 高架桥、路堑场景下的切换触发概率
在图13中,随着列车从P点移动至R点,四种算法的切换成功率随之增加,动态波束赋形-预留角算法和动态波束赋形-无波束预留角算法的性能相近,均优于A3切换算法和均匀波束赋形算法。

图13 高架桥、路堑场景下的切换成功率
图14对比了本文所提算法与传统A3切换算法和均匀波束赋形算法的切换时延。在25次仿真实验中,动态波束赋形算法的平均切换时延为110.96 ms,其时间开销相比传统A3切换算法和均匀波束赋形算法,分别增加了6.20%和5.11%。

图14 不同切换算法的时延对比
综上所述,路堑场景下的切换中断概率高于高架桥场景,切换触发概率和切换成功率低于高架桥场景,整体上运用基于LSTM的动态波束赋形算法后高架桥场景的切换性能更优。我国现行铁路无线通信系统对切换成功率的要求为大于等于99.5%[1],由图13及具体数据可知,相比A3切换算法和均匀波束赋形算法,采用动态波束赋形-预留角切换算法能够使列车在到达重叠区终点R之前就达到规定的切换成功率指标要求。具体地说,动态波束赋形预留角算法在路堑场景和高架桥场景下分别在距离R点之前的340、449 m处时即可达到指标要求,比均匀波束赋形算法对应的这一距离分别提前了300、440 m。
结合图13和图14的仿真分析可知,相比传统A3切换算法和均匀波束赋形算法,所提算法分别增加了6.20%和5.11%的时间开销,而路堑场景下的切换成功率分别提升了53.73%和16.01%,高架桥场景下的切换成功率分别提升了51.89%和22.92%。这说明,在略微牺牲切换时延的条件下,本文算法性能优于A3切换算法和均匀波束赋形算法。另一方面,根据仿真设置参数,计算可得列车经过重叠区的时间为12 s,所提算法的越区切换时延远小于12 s,说明列车在重叠区内能够顺利完成越区切换,算法设计具有可行性。
5 结论
本文提出一种应用于高铁通信场景的基于LSTM动态波束赋形的列车越区切换算法,通过增加动态波束增益解决eNB重叠区内列车越区切换成功率低导致的切换失败问题。基于中继通信模型给出了路堑运行场景中波束无遮挡传输的eNB天线高度设置规律;提出的基于神经网络的RSRP预测和k-Pa联合约束的动态波束增益分配算法,能够稳定预测未来时刻列车所需的波束赋形增益,为eNB总功率的合理分配提供依据;提出基于位置辅助的动态波束赋形机制,进一步提升了切换系统性能;为规避定位误差引起的波束赋形角度误差,采用增加预留角的策略实现动态波束赋形,同时结合不同场景下的路径损耗预测模型,对越区切换算法性能进行了评估。仿真数据表明,所提算法能有效预测未来时段列车的RSRP;对比A3切换算法和均匀波束赋形算法,重叠区内采用动态波束赋形-预留角策略的切换中断概率有了显著降低,切换触发概率和切换成功率有了明显提高,达到了规定的切换成功率指标要求。
未来工作中,将对5G-R系统中使用毫米波天线阵列实现更加集中、定向和更强功率的电磁波波束赋形传输方式解决传输路径上存在遮挡和强干扰的问题作进一步研究。
